曲线拟合的机械臂避障轨迹规划及仿真分析*

陈 雨，张晋轩

(广西大学行健文理学院，南宁 530005)

0 引言

工业机器人的广泛运用推动了工业行业改革与发展，工业机器人已经成为现代化工业必不可少的一部分[1]。

机械臂轨迹规划是研究机器人控制的重要内容[2]。轨迹规划描述动点在空间位置上的变化，研究机器人的关节角度变化，解决约束条件下机械臂作业完成问题。因此轨迹规划不仅影响机械臂作业过程中的平稳性,对控制的实时性和精确性也产生影响[2-3]。

为了保证机械臂平稳、精确和高效地作业，在机器人运动学基础上进行轨迹规划[4]。关节空间的轨迹规划和笛卡尔空间的轨迹规划是机械臂常用的轨迹规划方式[5]。文献[4]对切割机器人运动学建模，分别采用三次多项式、五次多项式和多项式混合插值法对隧道圆弧面的轨迹进行规划，通过比较各算法的优劣性寻求合适的轨迹规划算法。文献[6]拟合三次均匀B样条曲线，给出其表达式，使机械臂末端沿着曲线通过工件各加工点。文献[7]采用改进B样条曲线实现圆弧轨迹运动，提高机器人动作的平滑性，优化机器人的轨迹运动。文献[8]构造关节轨迹时采用5次B样条曲线的插值方法，任意配置起始点和停止点的速度和加速度，保持关节轨迹的速度和加速度的连续性，实现了机械手运动轨迹的平滑性。文献[9]针对机械臂运动轨迹的复杂多变性，规划了分段式轨迹，抓取起始段采用五次多项式的插值算法，抓取过渡段采用S型速度算法，最终抓取段采用NURBS曲线拟合算法,机械臂运行平稳,精度比较高,速度有所提升且轨迹光滑无拐点突变。

本文以埃夫特机械臂为研究对象，分析其运动学并建模。结合实际生产中存在机械臂动作路线有障碍物的特殊情况，需要重新规划线路绕过障碍物达到目标点。文中采用MATLAB的Robotics Toolbox工具箱仿真分析，分别利用ctraj()和jtraj()函数规划笛卡尔空间和关节空间的路径，前者的轨迹路线直接穿过障碍物，后者机械臂在基座底部大幅度摆动，超出关节轴的最大动作范围。因此，本文提出采用最小二乘法拟合三维空间路径点的曲线，让机械臂沿着曲线循迹成功绕过障碍物的方法。

1 运动学分析

埃夫特机械臂的操作空间如图1所示，机器人重量为3 kg，最大活动半径为760 mm，6轴允许最大转矩为4.6 Nm。

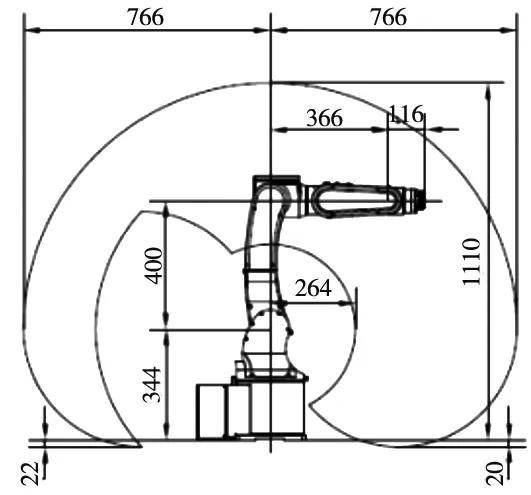
图1 机械臂的操作空间

机械臂由关节和连杆构成，关节转动导致连杆运动。多关节的组合运动可实现机械臂末端位姿的变化。

图2中，ai-1表示相邻两关节的z轴线之间距离；di表示相邻两关节的x轴线之间距离；αi-1表示相邻两关节的z轴线之间夹角；θi表示相邻两关节的x轴线之间夹角。根据各轴连杆之间几何关系得到改进型D-H参数如表1所示，其中a1=366 mm，d1=400 mm，d2=116 mm，θi=0。

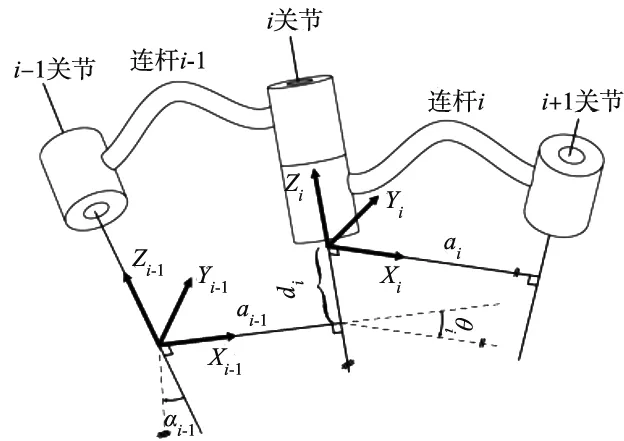
图2 连杆坐标系与改进型D-H参数

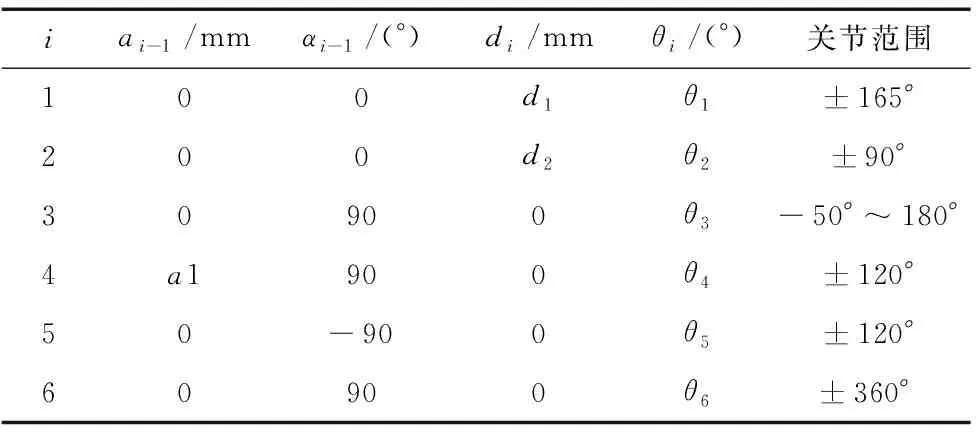
表1 改进型D-H参数表

使用MATLAB的Robotics Toolbox工具箱仿真3维模型，Link()函数创建连杆，SeriaLink()函数将连杆连接成机械臂，仿真结果如图3所示。

图3 机械臂3维模型

2 轨迹规划

轨迹规划可以使机械臂运动更平稳，减少不必要的震动和冲击，避免额外能量的消耗，减少机械元件的磨损[10]。

本文在工作台放置一长20 cm、宽30 cm和高25 cm的箱体障碍物，研究机械臂如何躲避障碍物的轨迹规划及仿真。

2.1 关节空间和笛卡尔空间规划

关节空间的轨迹规划和笛卡尔空间的轨迹规划是机械臂常用的轨迹规划方式[5]。关节空间轨迹规划将笛卡尔空间下的路径点转换成相对应的关节角度，对机器臂各个关节计算插值点，使各个关节同步动作且平滑到达目标点[11]。

图4使用工具箱自带的jtraj()函数规划关节空间的路径，机械臂在基座底部从起点到终点大幅度摆动，超出关节轴的最大动作范围。

笛卡尔空间轨迹规划通过求解逆运动学得到轨迹所对应的关节角度来完成整体的轨迹规划，运动路线比较直观。图5采用直线插补的算法，使用工具箱的ctraj()函数仿真，机械臂从起点到终点沿着直线穿过障碍物，不能完成避障任务。为满足轨迹的精确性和平滑性的要求并成功避障，本文提出采用最小二乘法拟合三维空间路径点的曲线，让机械臂沿着曲线循迹成功绕过障碍物的方法。

图4 关节空间运动轨迹 图5 笛卡尔空间运动轨迹

2.2 拟合曲线循迹

最小二乘法构造最佳匹配函数使误差平方和最小[12]。人为给定避障线路上的三维坐标点x=[x1,x2,…,xN]、y=[y1,y2,…,yN]和z=[z1,z2,…,zN]，使用polyfit()函数拟合一条最佳的曲线。

以空间的坐标点x为参考点，分别拟合出y=f(x)和z=f(x)两条二维曲线，把该两条二维曲线组合成空间三维曲线如图6所示。

图6 最小二乘法拟合空间三维曲线

设定轨迹起点位置T0=[0.7,0,0]，终点位置T1=[0,0.7,0]。当机械臂从起点到终点，只取两点位置动作时，利用jtraj()函数求解得到的关节角度值众多，机械臂6个轴无规则动作，不能绕过障碍物。

取拟合曲线上的中间点为过渡点，当机械臂沿着拟合曲线从起始点到过渡点、再到终点动作时成功绕过障碍物，轨迹路线如图7所示。

图7 机械臂成功避障

图8～图10描述机械臂在避障动作过程中多个关节的角度、角速度和角加速度的变化曲线，仿真过程设定起始点和终止点的角速度和角加速度都为0。由图8～图10可知作业过程中关节2、关节3、关节4和关节5做近乎平移动作，关节1和关节6做平移和旋转动作，减少了不必要的机械磨损。图10中，0～20采样点内机械臂从起始点到过渡点做加减速运动，21～40采样点内从过渡点到终止点做加减速运动，仿真结果与实际避障结果相符。避障过程中机械臂动作平缓稳定，无拐点、间断性变化，避免了突变引发的冲击震荡，降低机械性损伤，有效地提高机械臂的稳定性能和使用寿命。

图8 关节的角度变化曲线

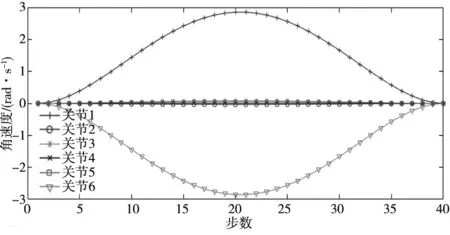
图9 关节的角速度变化曲线

图10 关节的角加速度变化曲线

3 结束语

本文以埃夫特机器人为研究对象，对其运动学进行了分析建模，结合实际生产中存在机械臂动作路线有障碍物的特殊情况，需要重新规划线路绕过障碍物达到目标点。文中首先分析了关节空间和笛卡尔空间两种不同轨迹规划方法，对比了机器人末端执行器的运动轨迹，前者机械臂在基座底部大幅度摆动，超出关节轴的最大动作范围，后者机械臂直接穿过障碍物。因此，本文提出采用最小二乘法拟合三维空间路径点的曲线，让机械臂沿着拟合曲线绕过障碍物的方法，仿真结果表明采用该方法机械臂成功避障。