基于改进BP神经网络的机床温度预警*

李泽阳，郑飂默，李备备，刘信君

(1. 中国科学院大学，北京 100049；2.中国科学院沈阳计算技术研究所，沈阳 110168；3.沈阳中科数控技术股份有限公司自动化装备事业部，沈阳 110168)

0 引言

随着运动控制工艺的发展与进步，在加工过程中，由于部件切削热、移动和旋转部件发热或由于机床结构设计不合理等原因，会造成机床局部发热而膨胀，进而影响加工零件精度。实际生产环境中，通常在机床加工发热位置安装温度传感器进行实时采集数据至工控机分析来避免温度产生的影响。但传统的过热保护仅是在发生过热时通过数控系统通知过热报警，无法达到温度预测的效果。因此，研究并设计一种基于实验数据建立的数学模型使之实现温度预警的方法十分必要。

近年来，BP神经网络由于其强大的非线性映照功能，出色的自组织和容错能力[1]，在网络安全[2]，故障诊断[3]，股票预测[4]，情境推荐[5]等不同专业领域得到充分运用，是目前最为成功的神经网络学习算法之一。但由于应用领域技术的快速发展，BP网络算法也出现了一些弊端，其中最为突出的是在学习过程中误差收敛速度过慢以及算法收敛效果不能将局部最优和全局最优区分开来等问题。国内外研究人员对此也提出了不同的改进方法和研究，袁圃等针对BP算法运算过程中隐含层节点数的选择问题，在最佳隐含层节点数下通过遗传算法优化BP网络模型的初始权重及阈值，进而解决了BP网络易陷入局部最优的缺欠[6]。王虹等为解决BP算法对初值敏感和易陷入局部最优解的问题，通过对粒子群的寻优计算式改进BP网络模型，有效地提高了数据融合精度和网络收敛速度[7]。Shi S等采用二次规划和广义最小二乘法对BP网络权重和阈值进行优化，提高了目标识别算法的精度[8]。

本文在算法学习过程中通过自适应学习率的方法改进BP神经网络。在完成数控机床温度传感器的采集数据后，运用MATLAB软件进行数据训练，将传统BP算法和针对学习率改进后的BP算法训练结果进行仿真对比和误差分析。实验仿真表明，采用自适应学习率的BP改进算法准确率更高，学习迭代次数更少，对数控机床温度过热预测具有积极的实际应用价值。

1 数据采集

以五轴数控机床作为研究对象，在热源(传动部件，如主轴)处安装温度传感器进行数据采集监测，采用ModbusTCP协议作为远程监控系统与数控机床之间传输数据的通信协议。温度传感器接入机床设备的子设备与连接方式步骤如下：

(1)子设备的处理选用双UART的ARM处理器，5V供电，供电通信采用USB接口的物理层，Modbus协议物理层接口采用RS485标准，整体设计如图1所示。

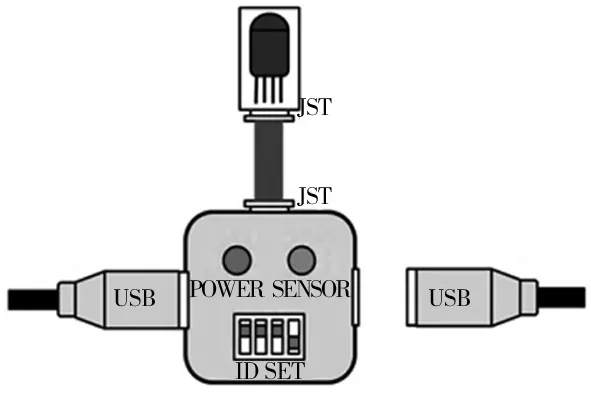
图1 电气设计

(2)主设备与子设备之间采用菊花链的形式串联起来，采用Master/Slave方式通信，其结构如图2所示。

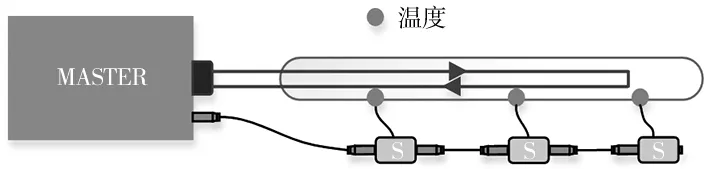
图2 主设备与子设备之间菊花链结构

实时获取的机床各温度传感器实时温度如表1所示，将表1中A组温度数据作为BP神经网络模型的训练集作为输入，B组温度数据作为测试集进行比较。

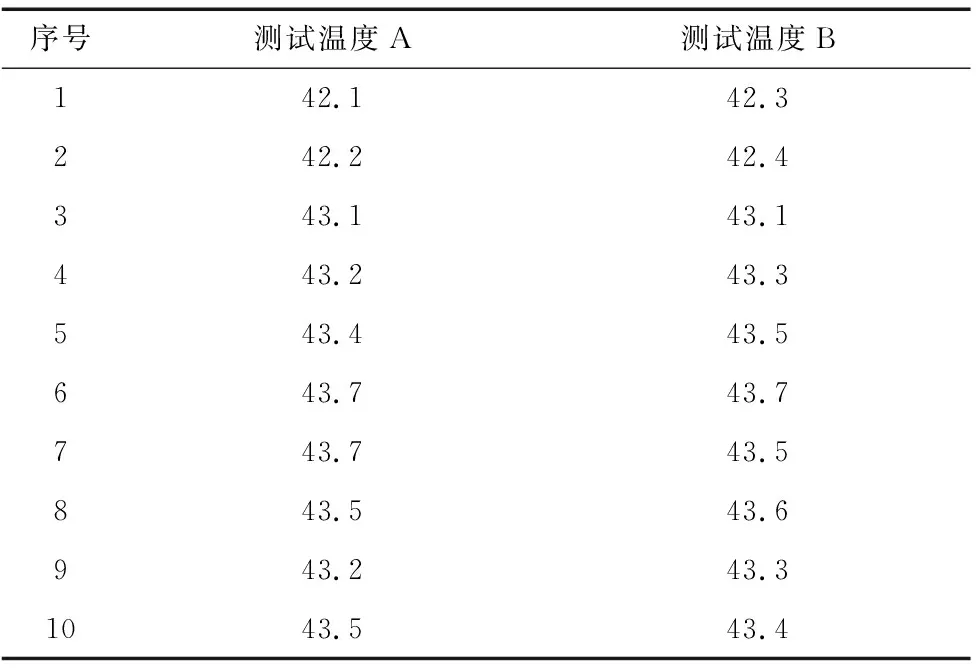
表1 实时测量温度值

2 BP神经网络算法设计

2.1 BP网络原理

BP神经网络是一种典型的非线性算法，通常由输入层、输出层和中间的隐含层组成[9]，每一层可以有若干个节点。各层之间节点的连接状态通过权重来体现。本文采用的温度预测模型如图3所示。

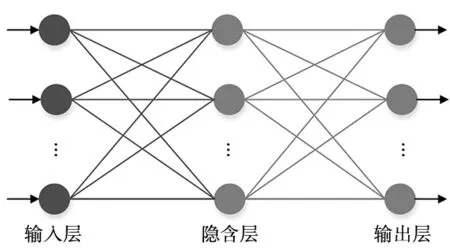
图3 基于BP神经网络的温度预测模型

经典BP算法分为两个过程，正向传播是指数据(或信息、信号)从输入端输入之后，沿着网络的指向，乘以对应的网络权重之后再加和，并将结果作为输入在激活函数中进行计算，将计算的结果作为输入传递给下一个节点。依次计算，直到得到最终的输出。反向传播是指将预测输出的结果与理想的输出结果进行比较，将预测输出结果与理想输出结果之间的误差利用网络进行反向传播的过程。具体的过程是通过多次迭代，不断地对网络上各个节点间所有的权重进行调整，权重调整的方法采用梯度下降法。

本文采用的BP网络机床温度预测模型的参数选定如下：

(1)激活函数

激活函数在预测网络输出结果和误差反向调节中起到重要作用。Sigmoid函数可以把任意输入的实数转换到[0,1]分布空间且函数具有非常好的对称性，故选用S型函数作为激活函数，表达式如下：

f(x)=(1+e-x)-1

(1)

(2)隐含层节点数目

BP网络的函数逼近能力与隐含层神经元数量有很大关联[10]。隐含层节点数量过多会使得算法收敛速度降低，过少将使得网络不能得到较好训练，最终结果精度不会很高。通过大量实验，估计隐含层节点的最佳数目经验表达式为：

(2)

其中，I、M和O分别表示网络输入、隐藏、输出三层神经元节点数，σ为范围在1～10之间的正整数。

(3)学习误差

定义样本中第k个神经元的误差函数为：

(3)

其中，EK为学习误差，Yi为真实值，yi为预测输出值。

2.2 算法改进

标准BP算法采用固定学习速率进行训练，通过梯度下降的思想寻找最佳权重，促使网络误差不断减小。网络的学习速率决定了学习过程中的权值变化[11]。学习速率过大，就会发生振荡现象，出现图4a的情况，即初始权重w0错过最优调整权重w′得到新权重w1，但w1和w′距离很远，需要进一步迭代学习。学习速率过小，会促使训练时长增加，网络收敛能力降低，出现图4b的情况，即初始权重w0按照梯度下降法搜索得到新权重w1，但w1距离最优调整权重w′较远，迭代效果不理想[12]。

(a) 学习率过大的情况 (b) 学习率过小的情况图4 学习速率较大与较小情况

由上述分析可得，如果算法学习速率能在训练过程中自动适应变化，则网络收敛速度和性能都能得到有效提高。本文通过比较本次迭代的学习误差与上次迭代的学习误差，采用灵活的学习速率进行训练来改进BP神经网络收敛过慢的缺陷。其数学表达式为：

(4)

其中，η(k)是第k次迭代学习速率，E(k)和E(k-1)分别是本次和上次学习误差函数值，λ1、λ2均为常数。具体的调整为，当本次误差函数值E(k)小于上一次学习误差值E(k-1)时，将学习速率η(k)扩大为η(k-1)的λ1倍，以加快收敛速度；当本次误差函数值E(k)大于上一次误差值E(k-1)时，将学习速率η(k)缩减为η(k-1)的λ2倍，以进一步探索权值最优点。

2.3 网络建模

本文BP网络结构均为单层结构，即输入层、隐藏层和以及输出层[13]。三层的神经元数目分别为a，b，c。输入样本集xi(i=1,2,…,a)表示输入层第i个节点的输入，隐含层输出节点为yj(j=1,2,…,b)，输出层输出节点为zn(n=1,2,…,c)。wij(i=1,2,…,a;j=1,2,…,b)表示输入层第i个神经元到隐含层第j个神经元的连接权值；vjn(j=1,2,…,b;n=1,2,…,c)表示隐含层第j个神经元到输出层第n个神经元的连接权值。θj(j=1,2,…,b)表示隐含层各神经元的输出阈值，γn(n=1,2,…,c)表示输出层各神经元的输出阈值。

为了缩小数量之间的相对关系和提高算法运算效率[14]，对网络各层输入、输出数据进行最值归一化处理，使得原始数据转换到[0,1]区间中，转换函数为：

(5)

其中，x′为归一化后的数据，x为原始样本数据，xmax为样本数据的最大值，xmin为样本数据的最小值。

采用自适应学习率的BP神经网络算法步骤为：

(1)初始化网络参数

连接权值wij、vjn，输出阈值θj、γn在区间[0,1]之间随机取值；设置收敛精度ε=0.01；表达式(4)中λ1=1.5，λ2=0.5。

(2)计算隐含层输入与输出

其中第j个神经元的输入为αi(j):

(6)

结合表达式(1)，隐含层第j个神经元的输出为αo(j)为:

(7)

其中，j=1,2,…,b。

(3)计算输出层输入与输出

其中第n个神经元的输入βi(n)为:

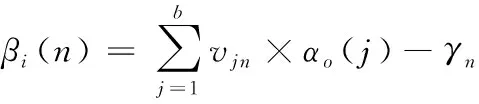
(8)

结合表达式(1)，输出层第n个神经元的输出βo(n)为：

(9)

其中，n= 1,2,…,c。

(4)输出层权值与阈值调整

由表达式(5)可得，输出层神经元的预测输出βo与样本中期望输出Y之间学习误差数学函数为：

(10)

基于链式法则，可得输出层权值调整表达式：

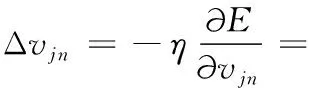
(11)

输出层阈值调整表达式为：

(12)

(5)隐含层权值与阈值调整

与步骤(4)同理，可得隐含层权值调整为：

(13)

隐含层阈值调整表达式为：

(14)

(6)更新各层权值和阈值，计算总误差Etotal：

(15)

(16)

(17)

(18)

(19)

若Etotal达到收敛精度标准或达到训练最大迭代次数，则结束训练，否则按照自适应学习率进行调整学习率，继续下一轮学习。温度预测模型流程如图5所示。

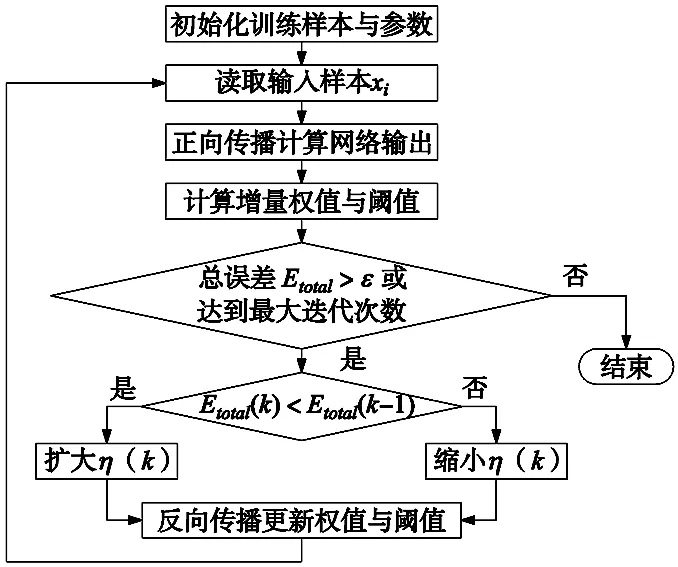
图5温度预测模型流程图

3 仿真实验与分析

3.1 参数设置

读取表1中A组实时温度数据作为输入数据，设定输入层、输出层神经元数量为I=10和O=10，取常数σ=1，根据公式(2)，可得隐含层神经元个数M=5。选用MATLAB作为计算机仿真平台，经过大量实验测试，设定标准BP的初始学习率η=0.047效果最佳，训练最大迭代次数为1000次，网络误差如果连续6次迭代没有变化则终止训练。

3.2 预测结果对比

进行网络建模，对训练样本进行拟合。标准BP神经网络与采用自适应学习率改进的BP神经网络预测温度值和真实温度值对比如图6所示。

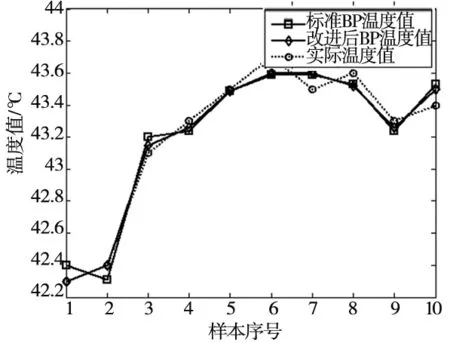
图6 预测温度与真实温度对比图

可以看出，在同样的训练样本下，改进后BP算法模型预测的温度值比标准BP算法精度更高，与真实温度值更为接近。

3.3 误差分析

标准BP算法和改进后的BP网络的误差曲线如图7所示。分析图7可得，采用标准BP神经网络的MSE(Mean Square Error，均方误差)在经过最大迭代次数1000次后接近于误差精度0.01，而采用自适学习率改进的BP网络模型仅在经历300余次迭代后达到误差精度要求。可知，采用自适应学习的BP算法经过更少的迭代次数便可满足误差精度要求，误差收敛速度相较标准BP算法更快。

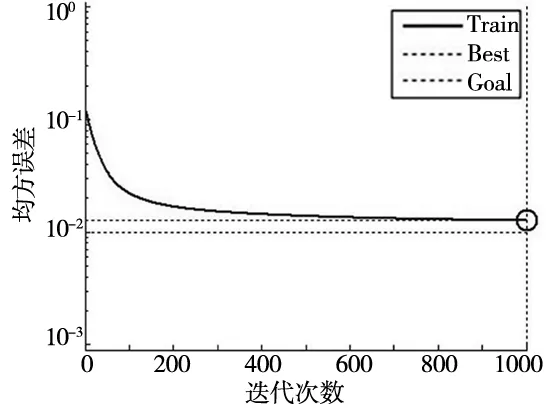
(a) 标准BP误差曲线图

(b) 改进后BP误差曲线图 图7 模型改进前后误差曲线图

为了评价温度预测模型的性能，本文引入MAPE(平均百分比误差)和RMSE(均方根误差)两项指标进行预测温度值与真实温度值之间的整体偏差估计。其计算表达式如下：

(20)

(21)

其中，Yi为真实值，yi为预测输出值。

同时考虑P(Precision，精确率)和R(Recall，召回率)两项评估指标[15]，计算标准BP模型和采用自适应学习率的BP模型评价参数如表2所示。

表2 模型改进前后的评价参数表

实验结果的数据表明，改进后的BP算法训练结果理想，对数控机床温度过热预测具有很好效果，能够较为准确的预测机床温度变化。

4 结论

本文针对数控机床由于温度过热产生热变形的问题，引入自适应学习率的改进BP神经网络作为温度预测模型。仿真结果表明，在确保误差精度的前提下，改进后的BP模型有效提高了算法收敛速度和网络性能。该研究的提前预测不仅提高了数控机床安全性，降低了机床维修费用，而且避免了因温度过热而造成的进一步损失，具有显著意义。