基于SWAT的金塔河流域综合干旱指数构建及其适用性分析
2021-09-28粟晓玲
梁 筝,粟晓玲,b
( 西北农林科技大学 a 水利与建筑工程学院,b 旱区农业水土工程教育部重点实验室,陕西 杨凌 712100)
干旱是指长时间的水分短缺造成的水资源供需不平衡现象,是一种成因复杂、发生频繁、影响广泛的自然现象[1-2],同时也是对我国社会经济影响最严重的气象灾害之一[3]。干旱通常分为气象干旱、农业干旱、水文干旱以及社会经济干旱4类,干旱指数在干旱分析中起着表征、度量和对比干旱程度的重要作用[4],是监测、评价和研究干旱发生、发展的基础[5]。常用的干旱指数有表征气象干旱的标准化降水指数[6](standardized precipitation index,SPI)和标准化降水蒸散发指数[7](standardized precipitation evapotranspiration index,SPEI),表征水文干旱的标准化径流指数[8](standardized runoff index,SRI)及表征农业干旱的标准化土壤湿度指数[9](standardized soil moisture index,SSI)等。不同类型的干旱分析需要不同的干旱变量,然而一些干旱变量的实测数据获取困难,水文模型作为一种间接获取干旱变量的方式被广泛应用。SWAT(soil and water assessment tool)模型是一种基于物理机制的、连续性的分布式水文模型[10],可应用于流域水文过程的模拟与管理,Zhang等[11]利用降雨数据及SWAT水文模型模拟出的蒸散发与土壤湿度等,构建了帕尔默干旱指数(palmer drought severity index,PDSI)、SPI以及SPEI等。
由于干旱成因的复杂性以及不同干旱变量之间的关联性,单一的变量无法表征干旱的全部特性[12],故构建多维变量的综合干旱指数可为干旱的监测、预防以及调控提供支持。综合干旱指数常用的构建方法有模糊综合法[13]、主成分分析法[14]、Copula函数联结法[15]等,但模糊综合法在赋权时存在一定的主观性,易造成误差;主成分分析法是将相关变量进行线性组合,无法反映变量间的非线性影响特征[15];而Copula函数能够将不同的边缘分布联结在一起,既保证了变量的独立性,又考虑了变量间的相关性,是目前最常用的分析方法之一。Hao等[16]采用Frank Copula函数联结SPI与SSI 2个指数,构建了气象农业综合干旱指数(multivariate standardized drought index,MSDI);李勤等[17]对上述指标进行了改进,以SPEI代替SPI,用非参数化方法联合SPEI和SSI,提出了改进的气象农业综合干旱指数(modified multivariate standardized drought index,MMSDI)。然而,Copula函数在联结三维及三维以上变量时具有一定的局限性[18-19],这种现象通常被称为“维数灾”[20],为了解决这一问题,目前常采用的联结高维变量的函数主要是非对称Copula函数。非对称Copula函数分为Pair Copula构造与嵌套Archimedean构造。Pair Copula构造多用于洪水频率分析[21],在综合干旱指数构建方面应用较少,且计算复杂;嵌套Archimedean构造方法简单且便于计算,但在多维干旱指数的研究中还不多见。为此,本研究以土壤湿度和蒸散发等实测资料较少的石羊河流域支流金塔河流域为对象,采用SWAT建立该地区的水文模型,模拟研究区缺失的气象水文资料,并与降雨、径流等实测数据相结合,通过参数化或非参数化方法构建单变量干旱指数SPEI、SSI以及SRI,采用非对称Copula函数中的嵌套Archimedean构造(nested archimedean construction,NAC)方法构建气象-农业-水文综合干旱指数(comprehensive drought index,CDI),并分析CDI的适用性,为干旱灾害的监测预报及评价提供科学依据。
1 研究区概况
金塔河是甘肃石羊河上游八大支流之一,起源于天祝藏族自治县境内的祁连山冷龙岭,该流域位于东经100°57′-104°12′,北纬37°02′-39°17′,地势南高北低,自西南向东北倾斜,平均海拔3 000 m,流域面积约841 km[22]。该流域属高寒半干旱半湿润区,年降雨量200~500 mm,年蒸发量700~1 200 mm,多年平均径流量达1.314亿m3。金塔河流域河道及水文站位置见图1。

1~13为子流域编号1-13 are numbers of sub-basins图1 金塔河流域水文站位置及子流域划分Fig.1 Hydrological stations and sub-basins division in the Jinta River Basin
2 研究方法
2.1 研究资料
SWAT模型主要的输入资料包括气象水文数据、数字高程模型(DEM)、土地利用类型图及其数据库、土壤分布类型图及其属性数据库。气象数据包括日降水量(P,mm)、日最高气温(Tmax,℃)、日最低气温(Tmin,℃)、日照时数(h)、风速(m/s)和相对湿度(%),时间尺度为1981-2017年,其中日降水量来源于CHIRPS(Climate Hazards Group InfraRed Precipitation with Station data)数据集(http://chg.geog.ucsb.edu/data/chirps/),该数据集是由美国地质调查局(USGS)和加利福尼亚大学气候危害小组联合开发,提供了从1981年至今的多时间尺度、多空间分辨率的降水数据;日温度数据来源于CN05.1格点化观测数据集,该数据集由吴佳等[23]利用国家气象中心2 400余个国家级台站(基本、基准和一般站)的观测资料采用“距平逼近”的方法插值得到[24];其余气象数据来自于甘肃省气象局(实测数据)和中国气象数据共享服务网(http://data.cma.cn/)。水文数据为金塔河河流出山口南营站1983-2017年月径流Q(m3/s)资料,来源于甘肃省水文局。数字高程模型来源于地理空间数据云(http://www.gscloud.cn),分辨率为90 m×90 m。土壤数据来源于世界粮农组织(FAO)提供的1∶100万土壤数据(HWSD, http://www.fao.org/nr/land/soils/harmonized-world-soil-databas-e/)。土地利用数据来源于地理国情监测云平台(http://www.dsac.cn/DataProduct/),分辨率为30 m×30 m。
2.2 SWAT 模型
SWAT模型是美国农业部农业研究中心(USDA-ARS)开发的适用于复杂流域、具有很强物理机制的分布式水文模型[25]。该模型将流域划分成若干个子流域,并依据子流域的土壤类型、土地利用方式及坡度将其划分成一个或多个水文响应单元(hydrologic response units,HRU),基于HRU分别进行土壤有效含水量、地表径流等的模拟。本研究选取的土地利用、土壤类型、坡度的阈值分别为5%,10%和10%,共划分了13个子流域(图1),282个HRU。
SWAT模型主要分为水文过程、土壤侵蚀和污染负荷3个子模块,本研究使用水文过程子模块,水文循环过程遵循以下水量平衡过程:
(1)
式中:SWt为土壤的最终含水量(mm),SW0为土壤的初始含水量,t为时间(d),i为计算时段,Rday,i、Qsurf,i、Eα,i、wseep,i、Qgw,i分别为第i天的降水量、地表径流量、蒸发蒸腾量、土壤坡面侧流量与渗流量、地下水回流量(mm)。其中,地表径流量采用径流曲线数法(soil conservation service, SCS)[26]模拟,蒸发蒸腾量采用Penman-Monteith公式[26]计算,土壤坡面侧流量采用动力蓄水模型[26]计算,渗流量采用土壤蓄水演算方法[26]计算,地下水回流量根据蓄水层补给量与基流回归系数得出。
采用SWAT-CUP中的SUFI-2算法对SWAT模型进行率定与验证。SWAT-CUP是由SWAT官网提供的用于辅助SWAT模型参数率定的工具,SUFI-2算法是SWAT-CUP中用于参数敏感性及不确定性分析的方法之一,该算法把通过拉丁超立方随机采样方法获取的参数与目标函数值进行回归分析,以判断参数的敏感性;同时采用95%置信水平上的预测不确定性区间带(95% prediction uncertainty, 95PPU)来表示变量的不确定性[25]。SUFI-2算法中对于不确定性分析的评价指标为P与R,其中P表示95PPU带所包含的实测数据的百分数,取值为0-1;R表示由实测数据标准差划分的95PPU区间的平均带宽,表示模拟值在95PPU带的分布程度,表达式为:
(2)
式中:Xu与Xl分别为模拟值的97.5%和2.5%的累积分布值,k为实测值的数量,σx为实测变量的标准偏差。模拟值分布越集中,则R值越小。
径流模拟精度采用确定性系数(R2)与Nash-Sutcliffe效率系数(ENS)来评价。R2描述的是模拟值与实测值变化趋势的一致性,其值越接近于1,表示精度越高;ENS描述的是模拟值与实测值的关系图与1∶1线的吻合程度,其值越接近1,表示精度越高[25]。R2与ENS的计算表达式如下:
(3)
(4)
2.3 单变量干旱指数的构建
2.3.1 参数化方法 选取合适的分布函数对不同时间尺度的干旱变量序列进行逐个拟合,采用极大似然法估计分布函数的参数,用K-S检验法进行拟合优度检验,利用AIC准则选取最优拟合函数,最后将各干旱变量序列的理论分布函数值逆标准化得出不同时间尺度的干旱指数[27]。本研究选取的分布函数有伽马分布、对数正态分布、威布尔分布、正态分布、Logistic分布。
根据AIC准则选取的最优拟合分布,将各干旱变量对应的拟合分布函数值逆标准化,即得参数化的干旱指数,表达式为:
DIP=φ-1P。
(5)
式中:DIp为参数化单变量干旱指数,φ为标准正态分布函数,P为理论分布函数值。
2.3.2 非参数化方法 在构建参数化干旱指数的过程中,若某种干旱变量的5种理论分布均不能通过K-S检验,则采用非参数化方法进行处理。采用Gringorten公式计算干旱变量的经验累积频率,表达式为:
(6)
式中:Pnonp为经验累积概率,i为变量序列升序时的次序,n为序列长度。
将经验累积概率逆标准化即为非参数化的干旱指数:
DInonp=φ-1Pnonp。
(7)
式中:DInonp为非参数化方法构建的干旱指数值。
2.4 综合干旱指数的构建
嵌套Archimedean构造属于Archimedean Copula的补充[28],可分为完全嵌套Archimedean构造(fully nested archimedean construction,FNAC)与部分嵌套Archimedean构造(partly nested archimedean construction,PNAC)。因本研究联合3个干旱变量u1、u2、u3,故采用FNAC方法构建综合干旱指数。FNAC的构造形式见图2。节点u1与u2连接形成CopulaC1(u1,u2),u3和C1(u1,u2)连接形成CopulaC2(u3,C1(u1,u2))。三维Copula由二维CopulaC1与C2组成,具有生成函数φ1和φ2。
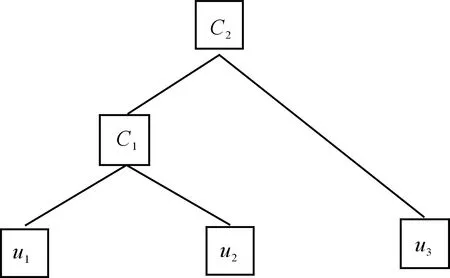
图2 完全嵌套Archimedean构造Fig.2 Fully nested Archimedean construction
三维Copula的表达式为:

(8)
式中:符号“∘”表示函数的复合,表示前两个变量连接形成1个二维Copula,这个二维Copula同另一个变量形成第二个Copula。式(8)表明,3个变量间的相依结构可以用2个二维Copula描述。一般来说,d维变量可自由指定d-1个节点和相应的分布参数,其余(d-1)(d-2)/2节点和参数通过构造隐式函数给出,而且满足参数条件θ1≥θ2≥…≥θd-1[28]。在Archimedean Copula函数中,Frank Copula函数在联合二维概率分布时对相关性的程度没有限制,且上下尾部的相关性变化均不明显,在干旱研究中应用较多,故本研究选取Frank Copula 函数作为FNAC中的连接函数。
采用FNAC联结三维干旱变量,得出参数化的三维联合干旱变量的概率,最后逆标准化得到三维干旱指数,即:
CDI=φ-1Pcom。
(9)
式中:CDI为构建的综合干旱指数,Pcom为三维变量联合累积概率。
3 结果与分析
3.1 SWAT模型的验证
构建金塔河流域SWAT模型,其预热期为1981-1982年,率定期为1983-2006年,验证期为2007-2017年。采用SWAT-CUP 2012中的SUFI-2算法对参数进行率定,并分析参数的敏感性。
选取与径流相关的23个参数进行全局敏感性分析,因参数的初始范围也是模型不确定性的来源之一,故各参数的初始范围均为SWAT-CUP所允许的最大参数范围。敏感性分析的目的是找出对模型模拟结果敏感性较强的参数,以提高模型的模拟效率。敏感性排名前5的参数及其最优值见表1。由表1可以看出,敏感性排名前5的参数分别是与地表径流形成有关的基流系数(ALPAH_BNK)和河道有效水力传导度 (CH_K2)、与融雪相关的参数降雪温度(SFTMP)和融雪基温(SMTMP)、与土壤水有关的土壤饱和水力传导度(SOL_K)。说明金塔河流域中冰雪融化所生成的径流对整个径流有较大影响,应对与地表径流和融雪相关的参数进行重点调参,这也与该流域的特征(有冰雪覆盖的高寒山区)相符。

表1 金塔河流域参数敏感性及最优值Table 1 Sensitivity analysis and final value range of parameters in the Jinta River Basin
采用P、R、R2与ENS来评价模型的适用性。图3为金塔河流域月径流率定期和验证期模拟结果与实测值的对比,其中,率定期P、R分别为0.88和1.44,满足P>0.7、R<1.5[29]的精度要求,径流模拟的不确定性在可接受的范围内。率定期与验证期的R2与ENS均高于0.7,模拟值与实测值拟合程度较高,率定后的模型参数可用于描述该流域的水文过程。
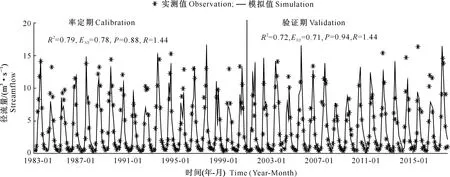
图3 金塔河流域率定期和验证期月径流量模拟值与实测值的对比Fig.3 Time series of simulated and observed monthly streamflow during calibration and validation periods in the Jinta River Basin
3.2 CDI的适用性分析
基于降雨、蒸散发、土壤湿度及径流等数据,运用参数化与非参数化方法构建金塔河各子流域1983-2017年年、季及月尺度的标准化干旱指数SPEI、SSI、SRI。其中,各个子流域的土壤湿度序列选取的最佳拟合函数多为正态分布,径流序列选取的最佳拟合分布多为威布尔分布与正态分布,降雨与蒸散发的差值序列选取的最佳拟合分布多为Logistic分布与正态分布,仅有9,10和13号子流域的土壤湿度序列未通过任何理论分布的K-S检验,故采用非参数化方法构建SSI。
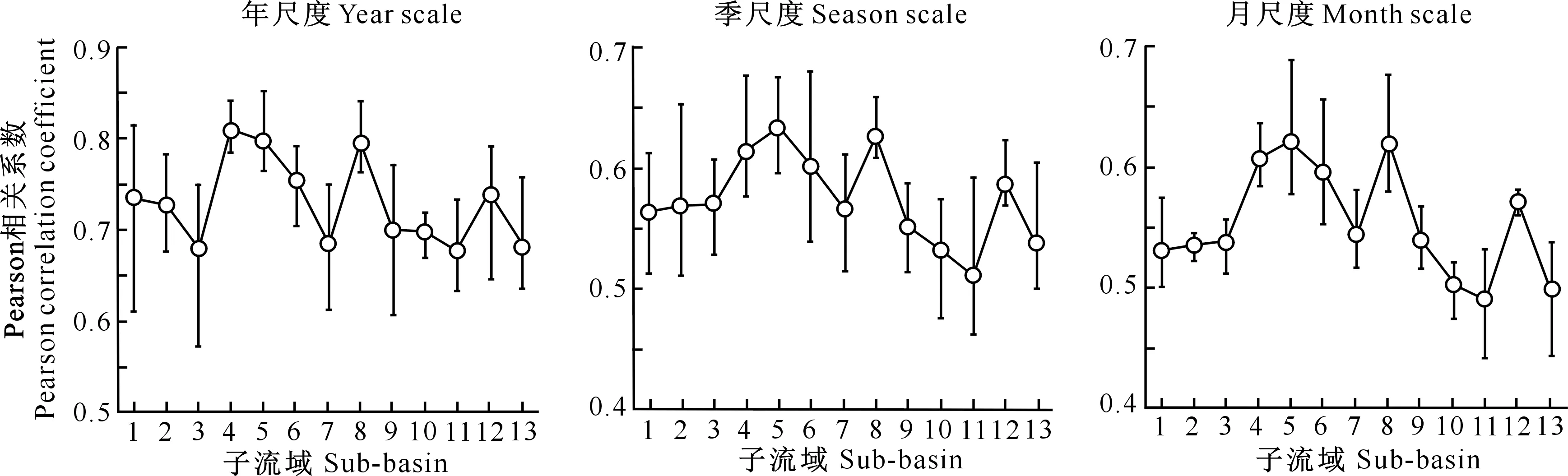
单变量干旱指数阈值划分参照SPI的划分标准[6],即干旱指数(I)> 0为无旱,-1 图4 金塔河流域年尺度SPEI、SSI、SRI与CDI时间变化曲线Fig.4 Time series of SPEI,SSI,SRI and CDI at annual scale in the Jinta River Basin 3.2.1 金塔河流域1991年夏旱、1992年春旱及2013年干旱特征 图5是金塔河流域1991年夏季尺度、1992年春季尺度及2013年尺度的SPEI、SSI、SRI、CDI所表征的不同类型干旱的干旱程度空间分布。由图5可知,1991年夏季SPEI监测到的气象干旱与农业干旱、水文干旱相比更加严重,仅6号子流域为轻旱,其余均为重旱或特旱;SSI监测的流域东部的农业干旱程度要高于流域西部,其中5和8号子流域均为重旱,2、10、11和13号子流域为轻旱,其余子流域均为中旱;SRI监测的流域西部的水文干旱程度高于流域东部,其中6、9、10和11号子流域均为重旱,2、3、4、5和7号子流域为中旱,其余子流域均为轻旱。CDI所表征的综合干旱在整个流域均达到了特旱等级。1992年春季农业干旱与水文干旱程度要重于气象干旱,SPEI所监测的气象干旱均为无旱,经查阅降雨资料,该地区于1992年5月份降雨量较大,缓解了当地的干旱状况;SSI所监测的农业干旱程度流域的北部强于南部,其中1、3、7、8和9号子流域为特旱,2和5号子流域为重旱;SRI监测的水文干旱仅1号子流域达到了特旱等级,2和3号子流域为重旱;CDI监测显示仅11号为轻旱,10和13号为中旱,5和12号为重旱,其余子流域均为特旱等级。2013年SPEI监测到的气象干旱程度最高,其中3、5、6、8和10号子流域为特旱等级,1、2、7和9号子流域为重旱,其余子流域均为中旱;SSI监测到的农业干旱程度较轻,无发生特旱、重旱的子流域,只有5、6和8号子流域为中旱,其余均为轻旱或无旱;SRI监测到的水文干旱程度重于农业干旱,其中6和7号子流域均为特旱;CDI表征的综合干旱仅在1、2和4号子流域为重旱,其余子流域均为特旱。 不同干旱指数在同一区域所表征的干旱程度不同,这表明单变量的干旱指数不能完全反映流域的全部干旱特征,且不同程度的干旱的空间分布也有差别。CDI表征的干旱程度与单变量干旱指数SPEI、SSI、SRI并不完全相同,这是由于三变量联合分布相对应的概率不等于其中任意一个变量分布相对应的概率[17]。CDI能监测到SPEI、SSI或SRI监测不到的干旱区域,表明该指数能够同时表征气象干旱、农业干旱和水文干旱,可从多个角度描述区域的干旱特性。 1~13为子流域编号 1-13 are numbers of sub-basins图5 金塔河流域1991年夏季、1992年春季及2013年SPEI、SSI、SRI与CDI的分布Fig.5 Distribution of SPEI,SSI,SRI and CDI in the Jinta River Basin in summer 1991,spring 1992 and 2013 3.2.2 SPEI、SSI、SRI与CDI的相关性 计算各子流域年尺度、季尺度与月尺度的SPEI、SSI、SRI与CDI的Pearson相关系数,结果见图6。图6中,单变量干旱指数SPEI、SSI、SRI与CDI的相关系数以区间图的方式展现,并取3个相关系数的均值分析不同子流域单变量干旱指数与CDI的相关程度,以进一步分析CDI的适用性。由图6可知,各子流域的相关性均通过α=0.1的显著性检验,不同时间尺度下SPEI、SSI、SRI与CDI均显著相关,说明CDI可用于描述研究区域的综合干旱特征。年尺度下单变量干旱指数与CDI的相关系数为0.55~0.85,其中4、5、6和8号子流域的相关性最强,相关系数均值均在0.75以上,以4号子流域相关系数均值最大,为0.81;其次是1、2、9、10和12号子流域,相关系数均值为0.70~0.75;其余子流域相关系数均值为0.65~0.70。季尺度下SPEI、SSI、SRI与CDI的相关系数为0.45~0.70,相关性最强的仍是4、5、6和8号子流域,相关系数均值均在0.60以上;其次是1~3号和7、9、12号子流域,相关系数均值在0.55~0.60;10、11和13号子流域的相关性较低,相关系数均值为0.50~0.55。月尺度下,SPEI、SSI、SRI与CDI的相关系数为0.45~0.70,相关性最强的子流域分别为4、5和8号,其相关系数均值均在0.60以上;其次是6和12号子流域,相关系数均值分别为0.59和0.57;1~3号和7、9、10号子流域的相关系数均值为0.50~0.55;11和13号子流域相关性较低,相关系数均值低于0.50。综上可知,4、5、6和8号子流域的单变量干旱指数与CDI的相关性最强,11和13号子流域的相关性较弱,说明位于流域东北部的4、5、6和8号子流域的综合干旱对气象干旱、农业干旱、水文干旱的监测能力较强;另外,年尺度的相关性强于季尺度与月尺度,月尺度的相关性最弱,说明年尺度的CDI对气象干旱、农业干旱与水文干旱的监测能力强于季尺度与月尺度。 图中所有相关系数均通过α=0.1的显著性检验All correlation coefficients in the figure passed the significance test of α=0.1图6 金塔河各子流域不同时间尺度下SPEI、SSI、SRI与CDI的Pearson相关系数Fig.6 Pearson correlation coefficients of SPEI,SSI,SRI and CDI at different time scales in each sub-basin of the Jinta River Basin 针对Copula函数在联合多维变量时存在的“维数灾”现象,采用嵌套Archimendean构造方法,基于现有的实测数据以及SWAT模型模拟数据,将蒸散发、降雨、土壤湿度、径流等多个干旱要素结合,构建可同时表征气象-农业-水文的综合干旱指数CDI,并分析该指数的适用性,主要结论如下: 1)构建的金塔河流域水文模型模拟径流的不确定性在可接受的范围内,率定期与验证期的精度指标R2与ENS均高于0.7,说明模型模拟精度达到标准,可用于模拟该流域的蒸散发、土壤湿度、径流等水文要素;敏感性分析表明,与地表径流和融雪径流相关的参数的敏感性较强,与该区域具有冰雪覆盖的地理特征相符。 2)为了研究CDI对研究区综合干旱状况的监测效果,选取1991年夏季、1992年春季以及2013年全年的干旱状况进行分析,结果发现CDI的干旱监测结果与实际干旱事件的发生基本一致,表明该指数可适用于研究区的干旱监测,可为该地区的防旱抗旱提供理论依据。 3)通过对比CDI与SPEI、SSI、SRI监测到的干旱区域,发现CDI能够监测到气象干旱、农业干旱、水文干旱监测不到的干旱区域,表明综合了降雨、蒸散发、土壤湿度与径流等多个干旱变量的综合干旱指数CDI能够同时表征气象干旱、农业干旱、水文干旱,可从多个角度描述研究区域的干旱特性。 4)为进一步分析CDI的适用性,对比金塔河流域各子流域不同时间尺度SPEI、SSI、SRI与CDI的相关性,结果表明,流域东北部的综合干旱对气象干旱、农业干旱、水文干旱的监测能力较强,其次是流域中部与西南部,且年尺度的CDI对气象干旱、农业干旱、水文干旱的监测能力强于季和月尺度。

4 结 论
