经历中感悟，练习中延伸——数学思想在教学中的实践与思考

■厦门市海沧区霞阳小学 周雪娜

数学思想是数学的灵魂，是对数学知识的本质认识。抽象思想、推理思想、模型思想是数学三大基本思想，并演变、发展出分类思想、方程思想、函数思想、归纳思想等较低层次的数学思想。2011版课标中“四基”的提出强调了数学思想的重要性。许多数学教师应及时跟进，引导学生投入猜想验证、合作探究、推理表达等参与知识创造的过程，在收获知识技能的同时，掌握数学思想方法，拓展思维。数学思想的渗透和影响，不仅要在教学目标中体现、在新授课过程中重视，更要在练习中有意识延伸，从而日积月累、潜移默化地提高学生的数学素养。

一、数形结合模型引路

数学是研究现实世界的数量关系和空间形式的科学，数与形既对立又统一。数形结合思想既包含使抽象的数学问题直观化的“以形助数”，也包含了使几何图形的规律和特点数据化的“以数解形”。在人教版五年级下册“长方体与正方体”这一单元中，数形结合的思想无处不在。例如，例1，结合长方体的实物进行观察、操作、记录，探究长方体这个基础立体图形的特征，同时归纳出可以从面、棱、顶点三个角度进行研究，形成研究立体图形的基本思路，迁移到后面进一步研究其他立体图形的学习中。又如，表面积、体积、容积的认识和公式模型的探索都紧扣立体图形表象及其特征，“形”为工具帮助学生理解和掌握知识，而非死记公式。

练习中的数学思想同样无处不在，挖掘练习中的数学思想需要教师提高自身素养，勤于思考，达到“润物无声”的境界。如下图练习题中的纸巾盒一题可以进行变式，提升“数形结合”的实效，培养学生的想象力。

原题：

（1）这个纸型盒的正面是什么形状？长和宽各是多少？和它相同的面是哪个？

（2）它的右面是什么形状？长和宽各是多少？和它相同的面是哪个？

（3）哪几个面的长是24cm，宽是12cm？

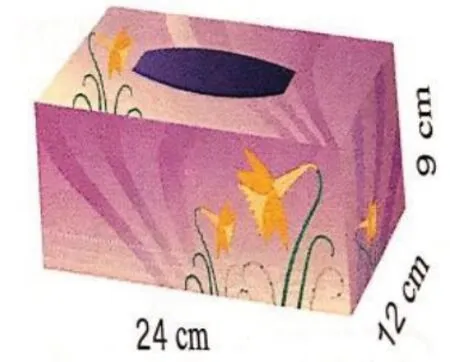
改编后：

将纸巾盒抽象成只有3条棱，想象：

这是什么图形？24厘米、12厘米、9厘米、分别是这个图形的哪条棱？这个图形哪个面长24厘米，宽9厘米？每个面的面积是多少？

改编后的图形其抽象程度提高了，目的在于让学生经历“由体想面”，培养空间观念，也为长方体表面积的学习打好基础。实践证明，同样的教学内容对数学思想、智力因素挖掘的程度不同，学生的思维发展会大相径庭。王永春教授在《小学数学与数学思想方法》中就提出了“高水平教学，标准化考试”的理念，教师在理解掌握基本的数学模型基础上应深入挖掘每一道练习中的数学思想和数学思维，帮助学生学会“数学地思考”。

二、善于转化，沟通联系

小学数学的编排体系遵循循序渐进、螺旋上升的特点。学生第一学段学习了平面图形的特征及面积和面积单位，为“长方体和正方体”这一单元的学习奠定了基础。如何求长方体的表面积呢？面对新的数学问题时，学生能自主把陌生知识转化为熟悉的知识，从而解决新问题就是转化思想的魅力之一。学生将立体图形的新知识转化成三年级平面图形的面积知识，再求出6个面的面积之和。善于转化不仅自主解决了问题，而且引出长方体表面积的概念。教师进一步拓宽表面积的概念，任何几何体外表面的面积之和就是它的表面积，建立表面积的一般意义。转化思想除了化未知为已知，还可以化繁为简、化一般为特殊、化抽象为具体等等。又如，在学习不规则物体的体积时，转化思想发挥了巨大作用：将橡皮泥这样不规则物体通过体积变形转化成规则物体来计算体积，形状虽变，但是体积不变，渗透了“变中有不变”的思想；像梨这样不可变形的不规则物体可以利用排水法，将不规则物体的体积转化为水的体积；排沙法、测质量法等均运用了转化思想测量物体的体积。

练习六有这样一道题：一个长方体饼干盒，长10cm，宽6cm，高12cm，如果围着它贴一圈商标纸（上下面不贴），这张商标纸的面积至少是多少㎡？学生不难发现商标纸的面积就是长方体4个侧面的面积之和，教师进一步引导学生想象并将商标展开，学生发现“立”起来的商标竟可以转化成长方形，长方体的侧面积也可以用底面周长×高，同时也为六年级学习圆柱侧面积计算方法做准备。又如，练习八第四题：题中小正方体的棱长数据刚好摆满心愿墙，可以用“总体积÷每个积木体积”求出这面心愿墙用了多少块积木。教师进一步修改数据将学生的思维引向深入：如果心愿墙与积木一样厚，则可以“化体为面”，再次体会转化思想的妙用，达到“让数学思想根植于儿童的数学学习”的目标。

三、运用推理，发展思维

推理是数学的基本思维方式，也是人们生活中经常使用的思维方式。曹培英老师用三棱锥图表示九大核心词及其关系，推理能力处在三角形底部的中心位置，可见其重要性。推理一般包括合情推理和演绎推理：合情推理用于探索思路、发现结论，常见的形式有归纳推理和类比推理；演绎推理用于证明结论。两种推理功能不同，在数学学习中都很重要，不能厚此薄彼。例如，在学习体积单位时先回顾旧知：测量长度用什么单位？测量面积用什么单位？进一步进行猜想：计量体积用什么单位？利用已有经验进行类比推理，认识到体积的测量也需要统一的标准，形成概念体系。在长方体的体积公式的探究过程中，学生通过动手操作、列表记录，数形结合思考，用不完全归纳法发现“每行的个数×行数×层数”与长方体长、宽、高之间的联系，理解体积公式的由来，并继续加以验证得到长方体的体积V=abh，这些都是合情推理的运用。正方体的体积公式推导则采用演绎推理：因为正方体是特殊的长方体，所以正方体的体积也可以用V=abh，又因为正方体的长=宽=高，所以V=a3。紧接着，学习容积时与体积进行类比推理，发现二者的相同点，都是指物体的体积，再用表格进行对比，梳理两者的异同点，加深对二者本质上的认识，在解决问题中能灵活进行应用。