基于改进SIRT算法的声学CT温度场重建*
2021-09-28孙灿烽王伊凡
颜 华,孙灿烽,王伊凡
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
声学CT温度场重建技术[1-3]通过测量声波从多个方向穿过被测区域的传播时间,推算被测区域的温度分布,具有非接触不干扰被测温度场、测温范围广、环境适应能力强、可实时监测等优点.作为世界上最先进的温度场测量方法之一,该技术备受学术界和工业界的青睐.工业锅炉温度场监测是其典型应用,而在深海热液口温度分布监测和仓储粮食温度分布监测中则处于探索阶段[4].
在声学CT温度场重建中,重建算法起着至关重要的作用.为了测量一个区域的温度分布,通常要将被测区域划分成若干个网格,每个网格重建出一个温度值,相当于一个原始的温度采样点.最小二乘法(least square method)、ART(algebraic reconstruction technique)算法和SIRT(simultaneous iterative reconstruction technique)算法[5-7]都是常用的声学CT温度场重建算法.这些算法要求被测区域划分的像素数要少于声波路径数,这意味着原始温度采样点很少.因此,当温度分布较复杂时,重建结果与实际分布偏差较大,甚至无法正确地重建出温度场特征.
与ART算法不同,SIRT算法对所有声波路径的误差同时进行校正,有效地降低了任一路径对温度场重建结果的影响,具有良好的抗噪能力和稳定性.但是当网格剖分数多于声波路径数时,SIRT算法重建的温度场中通常会出现很多噪点.针对此问题,本文提出一种改进的SIRT算法,通过专门设计的平滑滤波器,有效地抑制了网格剖分数多于声波路径数时重建温度场中的噪点,显著提高了其复杂温度场的重建能力.
1 声学CT温度场重建原理
声波在空气中的传播速度与温度之间的关系[3]可表示为
(1)
式中:c为气体介质中的声速;T为该气体介质的绝对温度;z为由气体组成成分决定的声音常数.
采用声学CT进行温度场重建时,要在被测区域的周围布置若干声波收发器,形成多条有效穿越被测区域的声波传播路径.测量出声波在各路径上的传播时间,采用适当的重建算法,可以重建出被测区域的声速分布,进而利用声速与温度的对应关系,得到被测区域内的温度分布.
2 改进SIRT温度场重建算法
声学CT温度场重建属于逆问题研究,通常要借助正问题模型来求解,因此,重建算法通常可分为正问题建模和逆问题求解两个环节.
2.1 正问题建模
声学CT的正问题是已知被测区域的温度(声速)分布和声波收发器的位置,求声波在各收发器间的传播时间.在被测区域周围均匀地布置一定数量的声波收发器,形成了M条有效穿越被测区域的声波路径.假设声波在第i条路径的传播时间为τi,其表达式为
(2)
式中:s(x,y)为声速倒数(声慢)的分布;dl为声波传播路径的积分微元.
将被测区域划分成N=n1×n2个网格(原始像素),并假定每个网格内的温度(声速)是均匀的,用sj表示第j个网格内的声慢,aij表示第i条声波路径在第j个网格的长度,则式(2)可改写为
(3)
令a=(aij)i=1,2,…,M;j=1,2,…,N,s=(s1,s2,…,sN)T,τ=(τ1,τ2,…,τM)T,则可建立声学CT温度场重建正问题模型为
τ=as
(4)
2.2 逆问题求解
当网格剖分数多于声波路径数时,SIRT算法重建的温度场中通常会出现很多噪点.平滑滤波是去除噪点的有效手段,为此本文将平滑滤波器与SIRT算法相结合,提出一种改进SIRT算法,即MSIRT算法.MSIRT算法包括内、外两个平滑滤波器,分别用于迭代过程中的声慢平滑和迭代停止后的温度平滑.MSIRT算法包括以下步骤:
1)初始化,为方程的初始解、松弛因子λ赋值,并令迭代次数k=0.
2)将第j(j=1,2,…,N)个网格的声慢修正为
(5)
式中,ρin为内层平滑滤波器算子,在迭代过程中对SIRT算法重建出的声慢实施平滑滤波.
3)判断是否满足迭代终止条件,如不满足则令k=k+1,回到步骤2)继续迭代修正.
4)利用声慢与温度的关系得到温度分布T′j,其表达式为
(6)
5)对温度分布T′j实施平滑滤波得到温度分布T″j,其表达式为
T″j=ρexT′j
(7)
式中,ρex为外层平滑滤波器算子,对迭代停止后得到的温度分布实施平滑滤波.
6)寻找温度分布T″j中的局部最大值,若网格j中的温度值为局部最大,则视其为热点,并将网格j的温度值用温度分布T′j中的对应值替代.
空间域的平滑滤波可采用邻域的平均或加权平均进行.若用Q表示像素(p0,q0)的包含(p0,q0)在内的邻域集合,(p,q)表示Q中的元素,f(p,q)表示像素(p,q)的灰度值,a(p,q)表示像素(p,q)的权重,则平滑处理后像素(p0,q0)的灰度值可表示为
(8)
本文采用高斯滤波器[8-9],即以高斯函数为加权函数,则有
(9)
式中,σ为高斯滤波器平滑程度方差,σ越大,平滑程度越好.采用高斯滤波器的主要原因有三点:1)高斯滤波器去除高斯噪声的效果很好,且在大多数情况下对其他类型的噪声也有很好的效果;2)高斯函数具有旋转对称性,可以保证滤波时各方向平滑程度相同;3)像素点离中心点越远,其权值越小,有利于保留图像的局部特征.
高斯滤波器由邻域(滤波器模板)大小和方差σ两个参数决定.方差或邻域过小时,对噪声抑制的效果不明显,而过大时易导致图像过平滑,丢失图像的细节特征.为简化滤波器设计,本文为ρin和ρex赋予同样大小的邻域,并为ρin赋予较小的方差,以保留更多的图像局部特征,为ρex赋予较大的方差,从而获得更好的噪声抑制效果.
平滑滤波器中心位于被测区域边界时,滤波器模板覆盖的区域会超出被测区域的边界.ρin和ρex分别采用镜像复制边界值和0值填充的方式获得边界外的值.因为0值填充有利于抑制出现在重建温度场边缘的伪热点,但如果ρin也采用0值填充的方式,多次迭代会严重降低重建温度场的温度值.
平滑滤波在抑制伪热点的同时,也会降低温度场中真热点的重建温度.由于内层平滑滤波对重建温度场中的伪热点进行了充分抑制,故本文假定迭代终止时重建温度场中的局部最大值为真热点.进行外层平滑滤波时,若网格j中的温度值为局部最大,则网格j的温度值不做平滑处理,仿真实验表明,该措施可以有效地降低热点温度重建误差.
3 常用的重建算法和重建误差评价
LSM为单步算法,其表达式为
s=(aTa)-1aTτ
(10)
ART、SIRT算法皆为迭代算法,其迭代公式分别为
(11)
(12)
常用的重建温度场误差评价主要有:重建温度场的平均相对误差Rave、均方根误差Rrms以及热点温度误差Rh,其表达式分别为
(13)
(14)
(15)

4 重建算法仿真验证
仿真研究可以建立各种温度分布,对算法重建温度场的能力进行充分细致地考核.本文将16个声波收发器均匀地布置在10 m×10 m的被测区域周围,形成96条有效声波路径,如图1所示.

图1 声波收发器及所形成的声波路径Fig.1 Acoustic transceivers and as-formed acoustic paths
采用LSM、ART、SIRT以及本文提出的MSIRT对式(16)~(18)所描述的模型温度场进行仿真重建.
热点位于(0.4,0.4)的单峰模型温度场为
(16)
热点位于(-2,-2)和(2,2)的双峰模型温度场为
(17)
热点位于(2,2)、(-2,2)、(-2,-2)和(2,-2)的四峰对称模型温度场为
(18)
采用LSM、ART和SIRT算法重建时,被测区域均匀地划分为8×8=64个网格,重建矩阵a条件数为19.31,ART和SIRT迭代次数分别设置为2 400和60次.采用MSIRT算法重建时,被测区域均匀地划分为12×12=144个网格,矩阵a条件数为54.10,迭代次数为60次,内、外层平滑滤波器的邻域为3×3,内层的高斯方差σ为0.33,外层的σ为0.55.为了更细致地描述温度场,本文给出的重建图像都采用三次样条插值[10-12]细化成31×31=961个像素.由于外推的精度通常难以保证,插值时只做内推运算.这意味着最外层原始像素点中心所界定的区域为细化像素的描述区域.
图2以单峰对称模型温度场为例,给出了飞行时间数据无噪声时ART、SIRT和MSIRT算法的平均相对误差随迭代次数的变化曲线.四种算法的重建时间如表1所示.由图2可以看出:1)三种重建算法的重建误差都能以较快地速度下降并趋于稳定;2)MSIRT算法的下降速度最快,稳定后的误差也最小.由表1可以看出,LSM重建时间最短,MSIRT重建时间最长,这是因为除LSM外的三种算法都是迭代算法,MSIRT的重建矩阵最大且有滤波环节.

图2 重建误差随迭代次数变化曲线Fig.2 Curves of reconstruction errors varying with iteration number

表1 重建时间Tab.1 Reconstruction time ms
图3~4分别为声波飞行时间数据无噪声和有噪声(添加标准差为0.001的高斯白噪声)时四种算法的重建误差比较.表2为模型温度场以及有噪声时LSM、ART、SIRT和MSIRT四种算法对应的重建温度场.由图3~4、表2可以看出:1)四种算法都可以正确地重建出温度场的基本特征,且具有较好的抗噪声能力;2)四种算法中,MSIRT的重建温度场与模型温度场最接近,重建误差最小,抗噪能力最强.
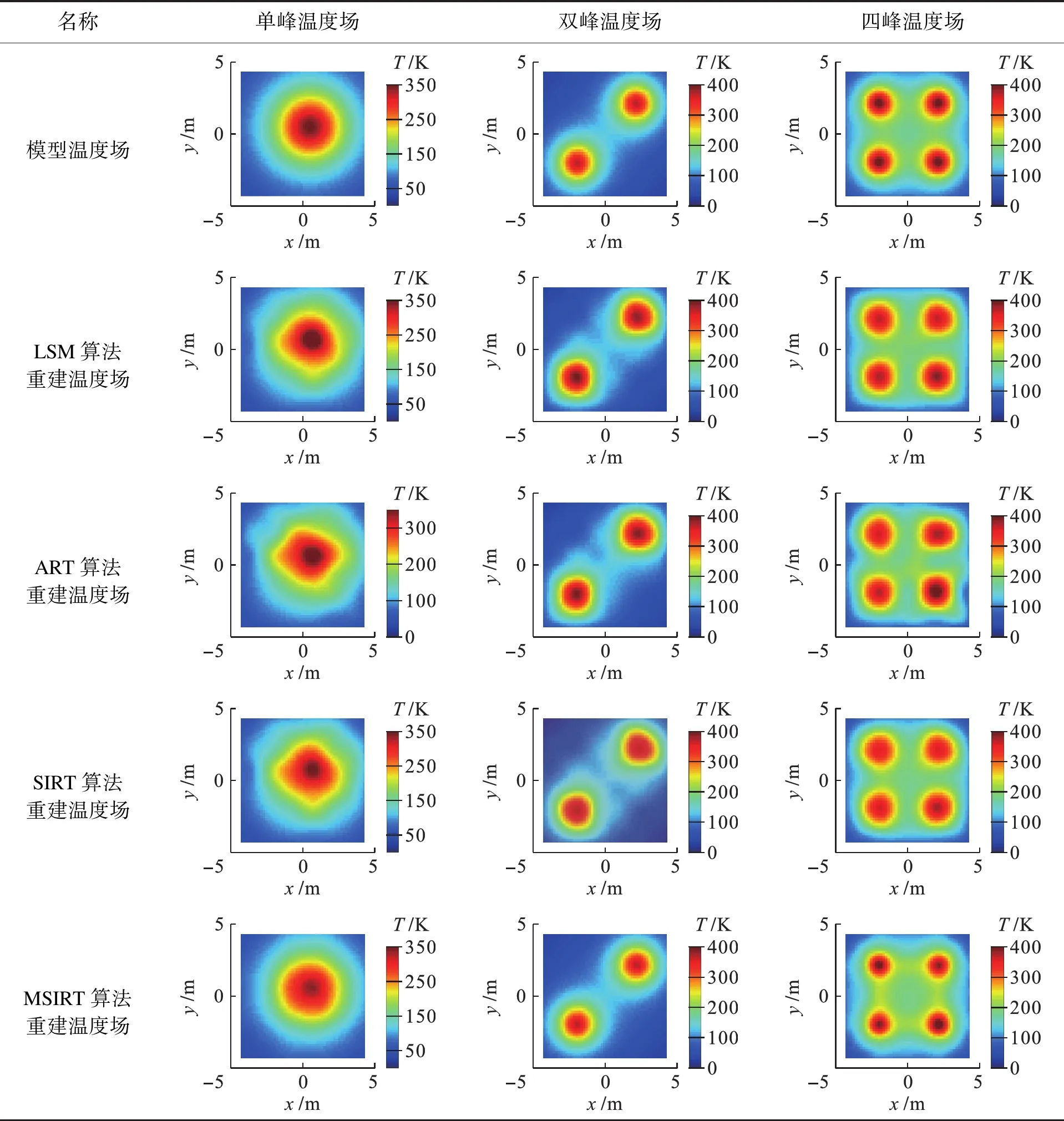
表2 模型温度场与声波飞行时间有噪声时的重建温度场Tab.2 Model temperature fields and reconstructed temperature fields with noisy acoustic travel time
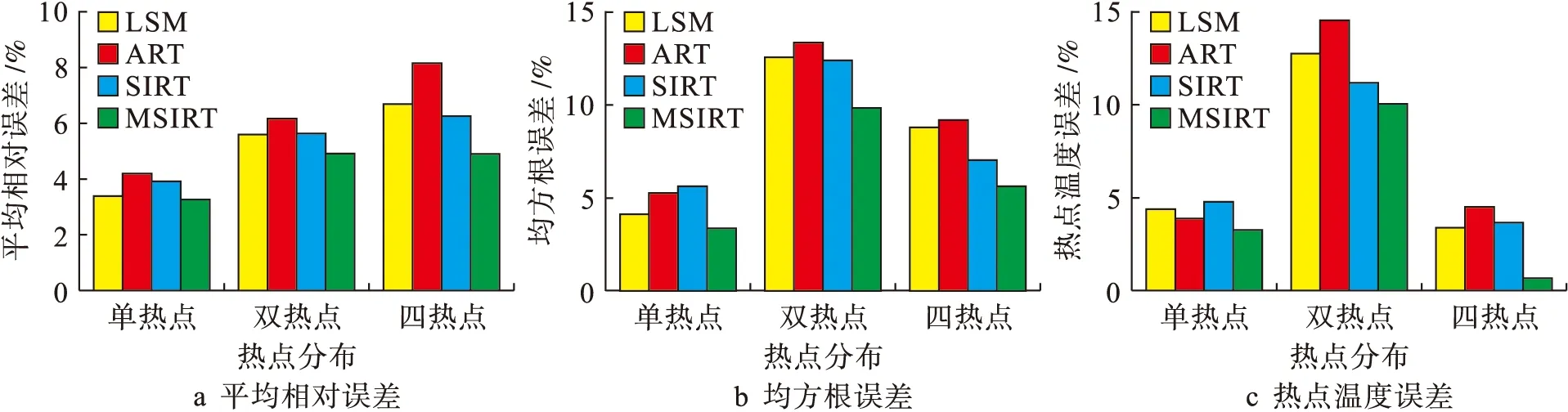
图3 声波飞行时间无噪声时的重建误差Fig.3 Reconstruction errors with noise-free acoustic travel time
5 重建算法实测数据验证
本文采用声学CT温度场重建系统进行了重建算法的实测数据验证.将8对声波收发器布置在1.5 m×1.5 m的区域周围,在被测区域正下方放置了一电热炉,形成单热点温度场,如图5所示.在每个测量周期内,扬声器按预定的顺序依次发出声波;各传声器接收声波并转换为电信号;电信号经信号调理后被同步采集到计算机中;计算机采用基于互相关的时延估计算法,根据这些数据计算出24条有效路径上的声波传播时间,获得一组实测数据.MSIRT算法重建时采用了8×8=64个网格,内、外层平滑滤波器的邻域为3×3,内、外层的高斯方差σ分别为0.33和0.65,迭代次数为100次.LSM、ART和SIRT算法重建时采用了3×3=9个网格,ART和SIRT的迭代次数分别设置为2 400和100次.表3为四种重建算法重建性能比较.图6为电热炉通电20 min后采集的一组实测数据所对应的重建温度场.此时用Fluke 54 Ⅱ和K型热电偶测得的被测层面最高温度为311.15 K,电热炉通电前该温度为291.15 K.由图6和表3可以看出:1)与LSM、ART和SIRT算法相比,MSIRT算法的重建温度场与实际温度场更接近,有明显优势;2)LSM重建时间最短,MSIRT重建时间最长,与表1相比,各算法的重建时间都有所缩短,这是因为实验系统的声线数和网格数都少于仿真系统的对应值,所以无论是重建还是滤波的计算量都会相应减少.

图4 声波飞行时间有噪声时的重建误差Fig.4 Reconstruction errors with noisy acoustic travel time

图5 收发器布局Fig.5 Transceiver layout

表3 四种算法重建性能比较Tab.3 Performance comparison of four algorithms

图6 实测数据重建温度场Fig.6 Temperature fields reconstructed by measured data
6 结 论
本文将平滑滤波器融入SIRT算法可有效抑制重建温度场中出现的大量噪点,降低重建误差.与SIRT、ART和LSM算法相比,本文提出的改进SIRT算法具有更好的复杂温度场重建能力.
对于同一个被测区域,周围布置的收发器数目越多,形成的有效声波路径数和区域允许划分的网格数越多,相应地重建系统的复杂温度场重建能力也越强.与此同时,完成一次周期测量所需要的声波数据采集时间越长,重建算法的运行时间也越长.由于各扬声器依次发出声波,且各声波信号间须有一定的时间间隔,所以即使是对于包含16个收发器的声学CT温度场重建系统,毫秒级别的MSIRT算法运行时间也远小于秒级别的一组声波数据采集时间.多线程设计可使数据采集程序与重建算法并行运行,因此,本文提出的MSIRT算法具有较大的实用价值.
