电网输电工程项目数据插补及造价预测融合模型*

乔慧婷，文上勇，黄 琰

(1.华北电力大学 电气与电子工程学院，北京 102206；2.南方电网能源发展研究院有限责任公司 技术经济中心，广州 510530)

随着我国社会用电量的持续增长以及电网技术水平的提升，电网工程项目的建设力度不断提高，电网公司面临着快速增长的建设周期压力与资金压力[1].电网的投资管理模式逐步从粗放式管理向精细化管理过渡，准确的工程造价预测是精细化管理的基础，其便于投资方与施工方制定合理的建设方案，缩短建设周期并提高项目资金投入的审核效率[2-3].

目前，电网公司通常基于传统的统计学方法对电网工程造价进行预测[4].由于电网工程造价影响因素复杂，造价系统具有多变性及非线性，传统的预测方法并不能很好适应，因此，较多学者基于机器学习算法对工程造价预测进行研究.宋宗耘等[5]通过增加高斯扰动参数，基于SVM算法进行工程造价预测；张宇晨等[6]针对影响因素众多的问题，采用主成分分析法进行处理，利用BP神经网络算法预测工程造价.杨凯等[7]为解决BP神经网络容易陷入局部最优的问题，提出一种GA-BP神经网络预测模型.上述研究均缺乏对数据缺失的深度处理，且单一的预测算法始终存在算法缺陷，无法在任何条件下对工程造价进行合理、准确的预测.

为了分析影响造价的主要因素，并解决数据采集过程中的数据缺失问题，本文重点针对电网工程项目的数据类型，基于数据挖掘的方法进行数据缺失的插补处理.结合机器学习回归类算法及决策树类算法中的优势，采用粒子群算法对岭回归、Lasso、随机森林、XGBoost 4种算法的权值寻优进行造价融合预测，提升工程造价的预测精度，并扩展预测模型的适用范围.

1 影响因素分析

电网输电线路工程造价的主要影响因素分为设备因素与自然因素两个部分，如表1所示.输电电压等级越高，对应的技术水平、材料品质、施工能力要求则越高，造价的成本也随之提高.通常工程回路数为单、双、三、四回路，回路数与造价成正比.在输电线路工程造价中，导线、塔材和杆塔的选型与造价密切相关，选型不同市场价格也不同.由于输电线路工程地理跨度广，一条线路可能途经山地、平原、丘陵、沙漠等不同地形.由于不同地形的工程造价成本不同，则需要计算途径地形的加权值.不同的地质条件造成施工中资源消耗不同，从而影响造价水平.例如：风速是输电线路工程设计中的重要考虑指标，为保证安全性，风速每增加5 m/s，输电线路的杆塔质量就需要相应地提高三成以上，造价相应也会随之增长；在高湿度、低温度的环境下，很有可能造成输电线路覆冰引发安全问题，从而需要提高线路承载限度消除隐患，最终也会导致项目的造价增高.

表1 输电线路工程造价主要影响因素Tab.1 Main influencing factors of transmission line project cost

2 基于随机森林的数据插补方法

在输电线路工程造价及相关重要因素的数据采集中，由于人为遗漏或丢失导致了部分数据的缺失.缺失数据的存在将会对机器学习模型的拟合效果带来严重的影响，因此需要对缺失值进行插补处理[8-9].传统的插补方法包括特殊值填充、均值填充、众数填充和线性填充等.由于传统的插补方法对样本的分布敏感且稳定性较差，因此目前常用插补方法进行数据挖掘.其原理是将缺失数据作为标签，并利用其余特征变量对缺失数据进行预测，对任何类型及分布的数据具有更优的拟合效果[10-11].常见的数据挖掘插补方法包括K最近距离邻法、回归法以及随机森林等，本文采用随机森林插补方法.

随机森林是基于CART决策树的集成算法，采取Bagging的集成思路.输入样本数量为M的数据集D，随机采样形成n个采样集，每个采样集同样具有M个样本.随机采样是一种有放回的采样方式，因此得到的采样集样本数量与数据集相同，但样本内容却有所不同.因为存在随机性，所以N个采样集样本内容也各不相同.利用采样集Dn训练n个CART决策树模型Gn(x)，连续型变量缺失数据采用n个决策树模型的回归结果平均值进行插补；分类型变量缺失数据则采用n个决策树模型的分类结果众数进行插补.随机森林的原理图如图1所示，由于随机森林的训练能够高度并行化，因此对大样本的训练速度具有优势，且采用随机采样训练出的模型方差小、泛化能力强.

图1 随机森林原理图Fig.1 Schematic principle of random forest

3 输电工程造价预测融合模型

电网输电工程造价属于连续型变量，因此选择基于线性回归的岭回归与Lasso算法以及基于决策树的随机森林与XGBoost算法进行预测[12].岭回归及Lasso算法通过在线性回归的损失函数上增加正则化项来优化影响电网工程造价的众多因素，解决最小二乘法存在的无法求解、方差大、参数含义不明确、模型泛化能力差等问题.XGBoost区别于随机森林的bagging集成思路，采用boosting集成思路，拟合每一次决策树迭代的误差，从而降低模型的偏差.但是单一算法均有自身的局限，因此本文赋予每个算法相对应的权值，相加进行融合提升4种算法的预测性能，基于粒子群算法确定4种算法的权值最优解.

3.1 粒子群算法

粒子群算法[13]是一种启发式算法，启发式算法以仿自然体算法为主，粒子群方法则模拟的是鸟群捕食行为.参数定义每个寻优问题解都是一只鸟，即“粒子”.m个粒子都在一个d维空间进行食物的搜索，粒子距食物的距离已知，方向未知.粒子i的当前位置pi及速度vi为

pi=(pi1，pi2，…，pid) (i=1，2，…，m)

(1)

vi=(vi1，vi2，…，vid) (i=1，2，…，m)

(2)

当前位置的优劣由一个确定的适应值进行判断，每一次迭代都以速度决定飞行的距离和方向.每一个粒子赋予了记忆功能，粒子i经过的历史最优位置opi表示为

opi=(opi1，opi2，…，opid) (i=1，2，…，m)

(3)

鸟群所经过的历史最优位置opg为

opg=(opg1，opg2，…，opgd)

(4)

(5)

(6)

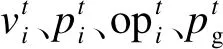
图2 粒子群算法流程图Fig.2 Flow chart of particle swarm optimization algorithm

3.2 融合模型

本文设计的融合模型流程如图3所示，通过岭回归、Lasso、随机森林、XGBoost 4种算法分别对训练数据集进行造价预测得到参数F1(X)、F2(X)、F3(X)、F4(X)，最终得到构造融合模型F(X)表达式为

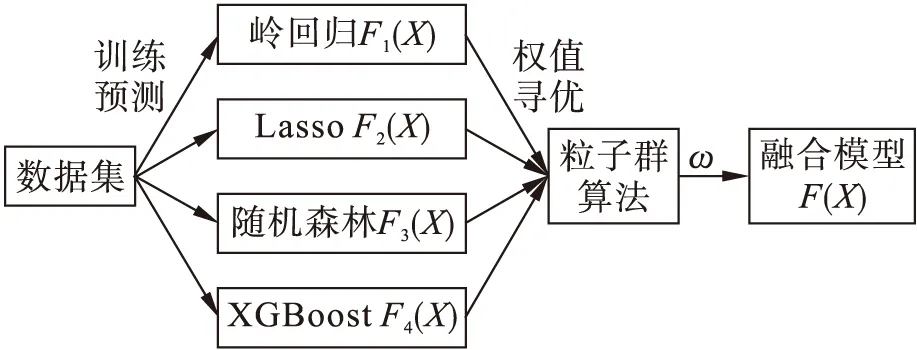
图3 融合模型流程图Fig.3 Flow chart of fusion model

(7)

式中，ωj为算法的权重，需要通过粒子群算法计算出ωj的最优解.

构造目标函数为

L(Y，F(X))=|Y-F(X)|

(8)

4 实验验证

本文选取160个电网输电线路工程项目进行实验，部分样本数据如表2所示，“-”表示缺失值.

表2 输电线路工程部分样本数据Tab.2 Part of sample data of transmission line engineering

首先对分类型变量进行量化处理：输电电压等级110 kV映射为1，220 kV映射为2；回路数单、双、三、四分别映射为1、2、3、4；1～8分别对应地质类型：松软土、普通土、坚土、砂砾坚土、软石、次坚石、坚石、特坚石；地形类型分为平原、丘陵、山地、高原和平地5类，分别映射为1～5.对于包含同一变量不同类别的线路，采取加权平均的方式进行取数，所有项目的数据缺失情况如表3所示.除了单位造价和输电电压等级之外，其余变量均存在不同程度的缺失，平均缺失占比10%左右，其中风速最高达到了20%的缺失占比.

表3 输电线路工程项目数据缺失情况Tab.3 Missing data of transmission line project

为了验证插补方法的效果，筛选出具有完整数据的108个工程项目.除单位造价变量之外，其余变量随机缺失10%的数据，完成插补后将预测的数据与实际数据进行比对.连续型变量数据通过均方根误差RMSE和平均绝对百分比误差MAPE指标进行评价[14]，数值越接近0表示模型效果越好；分类型变量数据的评价指标采取准确率与F1值[15]，准确率取值范围为[0，1]，数值越接近1说明模型效果越优，F1值是精准率和召回率的调和平均数，从而消除了不平衡样本带来的影响，F1的数值越高说明其性能越好.采用学习曲线和网格搜索的方式对随机森林进行参数调优，重要参数调参结果如表4所示.

表4 随机森林调参结果Tab.4 Results of random forest parameter adjustment

传统均值/众数插补法与随机森林插补法的对比评价结果如表5所示，数值为特征变量评价结果的均值.表5中随机森林插补法的插补效果明显优于传统方法，故本文选取随机森林法对所有缺失数据进行插补.

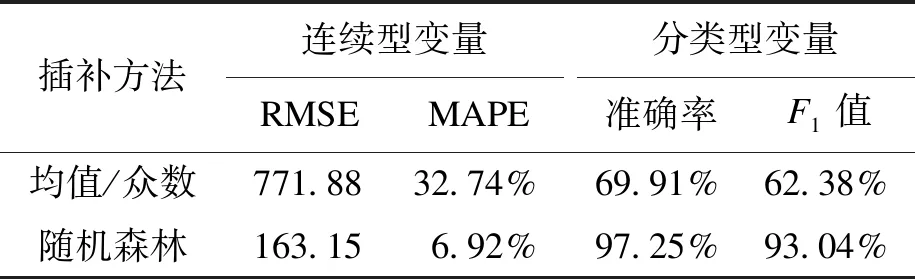
表5 插补评价结果Tab.5 Evaluation results for interpolation

以单位造价作为预测目标，其余特征变量进行标准化处理.随机选取75%样本，即120个样本建立岭回归、Lasso、随机森林、XGBoost预测模型，利用剩余的40个样本进行测试，采取RMSE、MAPE指标进行模型预测效果评价.粒子群算法的初始化参数设置如下：空间维度d=4；粒子数量m=100；位置初始范围[-10，10]；速度初始范围[0，1]；惯性权重μ=0.6；学习因子c1=c2=2；r1、r2∈[0，1]；最大迭代次数为500.当迭代到474次时，最优适应值基本稳定，迭代到500次时，最优适应值达到最小值66 710.此时，权值为(0.624 7，-0.399 5，0.360 6，0.415 6)，得到融合模型F(X).

对比4种单一算法模型、average融合模型(4种算法预测值取平均)、权值融合模型在测试集中的表现效果如图4所示.评价指标RMSE、MAPE对比结果如图5所示.由图4、5可以看出模型的预测效果由优到劣的顺序为：权值融合模型、average融合模型、XGBoost模型、随机森林模型、岭回归模型、Lasso模型.权值融合模型的RMSE为87 615，MAPE仅为2.17%；相比average融合模型RMSE降低了23 493，MAPE降低了0.84%.说明融合模型相较单一算法可以有效提升模型的预测准确性，并且本文提出的权值融合模型相较一般的融合模型预测准确性更高.

图4 模型预测值与实际值对比图Fig.4 Comparison between model-predicted and actual values

图5 模型评价指标结果Fig.5 Results of model evaluation indexes

5 结 论

针对电网工程项目数据缺失导致造价难以预测的问题，本文重点分析了不同类别数据缺失插补的数据挖掘方法.对于输电线路工程项目的数据，采取了不同评价指标进行插补效果评价，随机森林插补法表现最优，能够较为准确地对不同类型的缺失数据进行插补.为了克服单一算法预测造价的局限性，采用粒子群算法计算多种算法的最优组合权值，并进行融合预测.预测结果表明，融合算法使得RMSE和MAPE两项指标均得以降低，实现了单位造价的精准预测.在后续的研究中，将尝试使用Stacking、Blending等融合方法进行单位造价的预测，进一步提升预测的精准性.