考虑时效损伤的岩石黏弹塑性本构模型

曹利军，马 超，王 伟

（水发规划设计有限公司，济南250014）

蠕变特性是指材料受外界荷载、化学作用、温度、水等因素的影响，其应变表现出显著的时效特性［1］。岩石蠕变特性关系到岩体工程长期稳定性，是实际工程中必须重视的内容之一［2］。岩石在外界应力条件下蠕变变形逐渐累积，外界应力条件改变影响蠕变变形发展，达到一定应力水准时，岩石便表现出加速蠕变行为，短时间内岩石破坏，巷道隧洞、高边坡、核废料储存室、油田套管失稳破坏常常与应力条件改变导致的岩石加速蠕变行为有关，因此在岩体工程全寿命周期中，岩石蠕变特性不可忽视［3，4］。

本构模型是描述岩石蠕变特性的核心手段，通过不同元件自由组合而成的元件模型由于其灵活性得到了广泛应用，但建立能精准识别不同类型岩石蠕变行为（尤其是加速蠕变）的本构模型仍是一个难点。Shibata等［5］通过搭建蠕变应变率与流变参数之间的联系，建立可较好描述凝灰岩蠕变行为的本构模型；Günther 等［6］开展不同应力和温度下的盐岩蠕变试验，通过建立稳态蠕变速率和外界影响因素之间的关系，得到了较为精准的盐岩蠕变模型；唐佳等［7］以白云石英片岩和绿泥钠长片岩为研究对象，构建了能反映黏弹塑性偏量特征的改进Burgers模型；卢军振［8］针对硬岩的脆性蠕变破坏现象，探究硬岩脆性蠕变破坏时间和破坏后的应力变形之间的联系，从而建立能较好表征硬岩蠕变行为的本构模型；黄海峰等［9］引入分数阶微积分来描述软岩蠕变的黏弹性和黏塑性应变，与损伤弹性体串联，得到一个新的蠕变损伤模型，并证明能较好地反映软岩蠕变变形特征；金俊超等［10］提出一种基于应变软化指标的蠕变力学模型，能较好地模拟泥岩和砂岩蠕变现象。

目前已有大量蠕变本构模型，但多数模型难以同时描述软岩和硬岩的加速蠕变行为，鉴于此，本文以广义Burgers 模型作为基础模型，引入损伤力学理论，建立考虑时效损伤的黏塑性体，从而建立一维岩石黏弹塑性蠕变损伤模型，并推广至三维应力状态。给出模型参数求取方法，并进行参数敏感性分析。采用所建模型辨识5 种不同坚硬程度岩石的蠕变试验数据，验证所建模型的合理性和适用性。

1 蠕变损伤模型的建立

1.1 基础模型的选择

岩石作为一种复杂的非线性地质材料，其内部同时赋存着弹性、黏性、黏弹性和黏塑性特征，元件模型理论［1］中常用的有弹性元件、黏性元件和塑性元件，但单一的某个元件难以准确描述材料蠕变性质，因此需对不同元件进行自由组合从而得到组合元件模型。传统Burgers 模型是组合元件模型中的一类经典模型，被众多学者［1，7，8］证明能较好地描述岩石衰减、稳定蠕变，但部分学者发现［11，12］传统Burgers 模型描述硬岩蠕变特征时误差较大，由此学者们在传统Burgers 模型的基础上，串联了一个Kelvin 体，得到了适用范围更广的广义Burgers 蠕变模型［11］，广义Burgers蠕变模型示意图如图1所示。

由图1可看出，广义Burgers模型与传统Burgers模型不同之处在于多串联了一下Kelvin体，其蠕变状态方程为

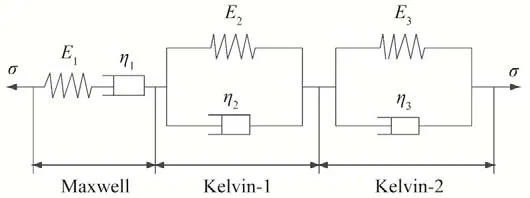
图1 广义Burgers蠕变模型Fig.1 Generalized Burgers creep model

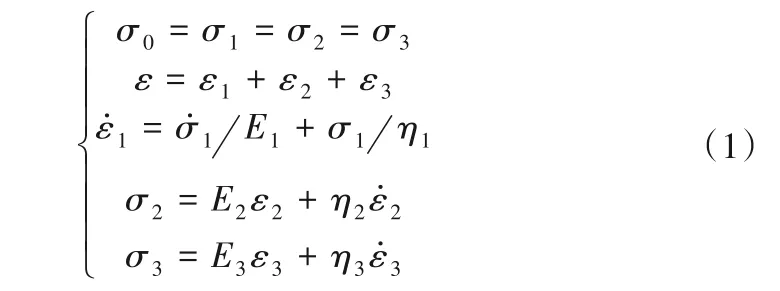
式中：σ0为初始应力；σ1、ε1、E1和η1分别为Maxwell体的应力、应变、弹性模量和黏滞系数；σ2、ε2、E2和η2分别为Kelvin-1体的应力、应变、弹性模量和黏滞系数；σ3、ε3、E3和η3分别为Kelvin-2体的应力、应变、弹性模量和黏滞系数；上标圆点表示某变量对时间t的一阶导数。

通过对式（1）进行求解得到广义Burgers 模型的一维蠕变方程：

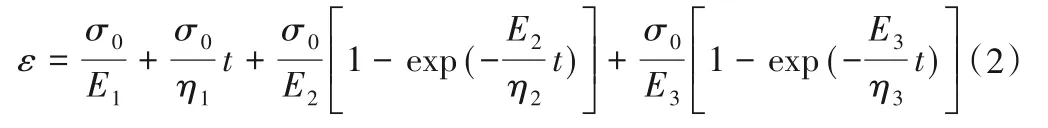
引用文献［13，14］中的大理岩和辉绿岩蠕变试验数据，利用数学软件Origin，基于Levenberg-Marquardt 算法，验证一维广义Burgers 模型和一维传统Burgers 模型描述硬岩稳定蠕变行为的差异，对比验证结果如图2所示。

由图2 可知，传统Burgers 模型拟合曲线形态相对固定，衰减、稳定蠕变阶段之间部分较为“外凸”，理论值远高于试验值，稳定蠕变阶段理论值曲线近似为直线性线段，该阶段快结束部分的曲线明显高于理论值，传统Burgers模型对大理岩和花岗岩的拟合效果一般，R2分别为0.933 8 和0.957 7，广义Burgers 模型对大理岩和花岗岩的拟合效果较好，R2分别为0.999 0 和0.990 5。鉴于广义Burgers模型描述硬岩稳定蠕变的优越性，考虑到蠕变模型对不同种类、不同硬度岩石的适用性，择取适用范围更广的广义Burgers模型作为本文模型的基础模型。

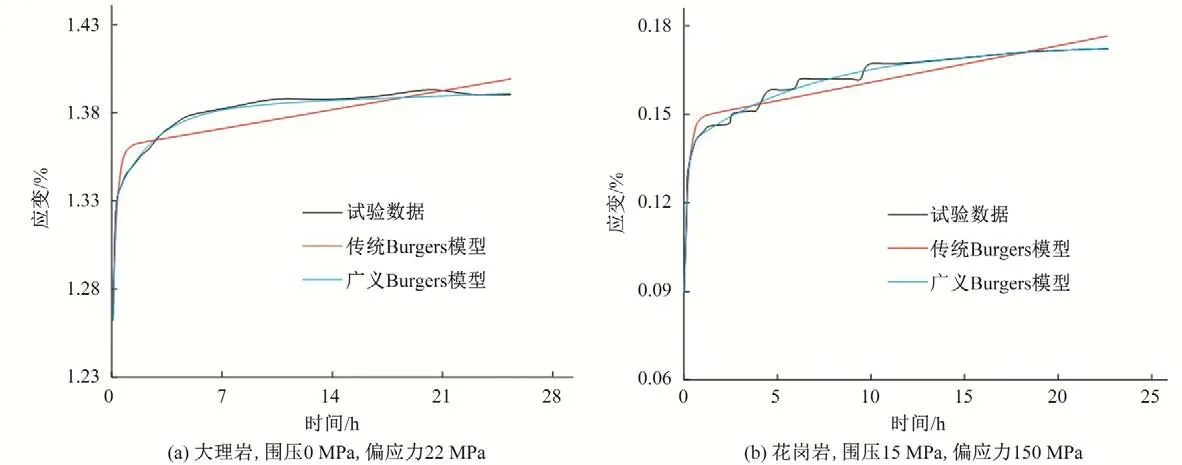
图2 对比验证曲线Fig.2 Comparison validation curves

1.2 考虑时效损伤的黏塑性体

广义Burgers 蠕变模型结构为H-N-H｜N-H｜N-N｜S，具备一定的反映岩石弹性、黏性、黏弹性变形特征的能力，但无法描述岩石的黏塑性变形。由此引入一个黏塑性体，其微分本构方程为

当应力超过损伤应力阈值（即长期强度），岩石材料才能进入加速蠕变阶段，该阶段黏塑性变形急剧增加，岩石材料内部微裂纹不断发育和扩展，内部损伤不断累积，造成岩石力学性能的宏观劣化［9］。由此在黏塑性体的基础上，引入损伤力学理论，根据Lemaitre等效应力原理［15］，将式（3）变形为：

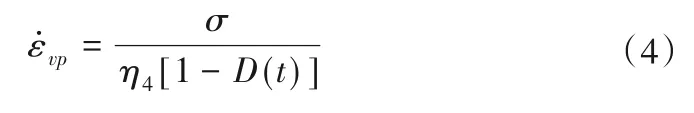
式中：D（t）为损伤变量。

这里需注意的是，部分学者［16，17］按照Lemaitre 应变等效原理进行损伤演化时，直接将本构方程中的应力替换成等效应力，譬如将直接替换为，这样的做法是不对的。实际上损伤变量是关于时间的函数，积分后D（t）会发生变化，正确的方法应该是将微分本构方程中的应力替换成等效应力，例如本文式（3）演化为式（4）的方式［18］。

Kachanov［19］认为在一维应力状态下，蠕变条件下的损伤发展方程为：

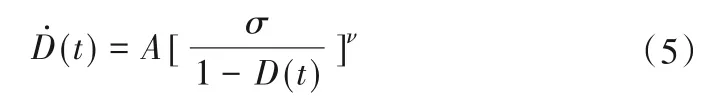
式中：A和ν为材料参数。

对式（5）进行积分可得蠕变破坏时间te为：

联立式（5）和式（6）可得D的演化规律：

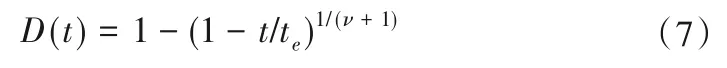
将式（7）代入式（4）得：

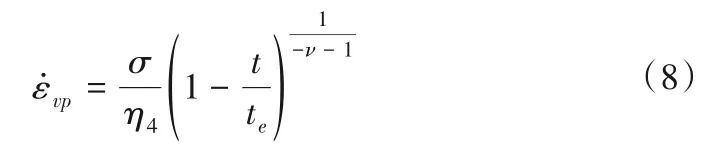
对式（8）进行积分可得：

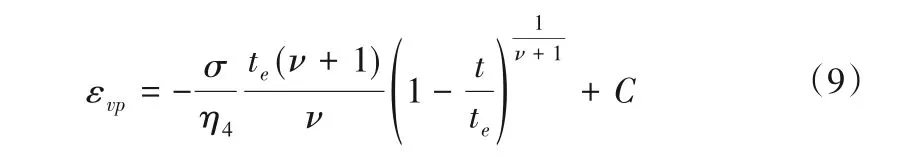
式中：C为积分常数。

当t=0时，黏塑性应变为零，将该条件代入式（9）有：

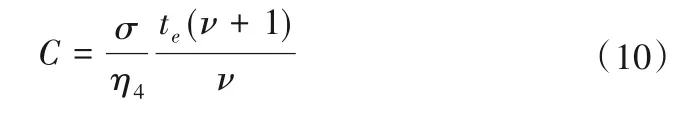
将式（10）代入式（9）变形可得：

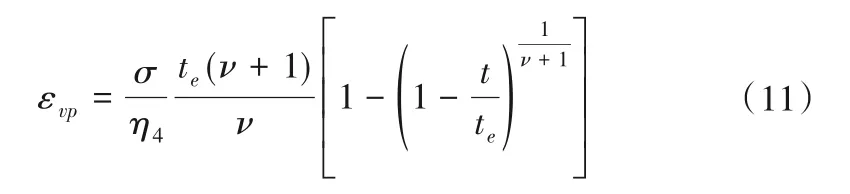
式（11）即为考虑时效损伤的黏塑性体。

1.3 一维条件下的蠕变损伤模型

为使蠕变本构模型可同时反映岩石弹性、黏性、黏弹性和黏塑性特征，将考虑时效损伤的黏塑性体与广义Burgers模型串联，得到一个新的蠕变损伤模型，如图3所示。

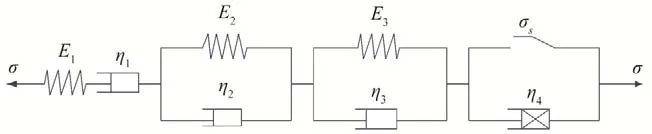
图3 蠕变损伤模型Fig.3 Creep damage model

结合式（2）和（11）得到一维条件下的蠕变本构方程：

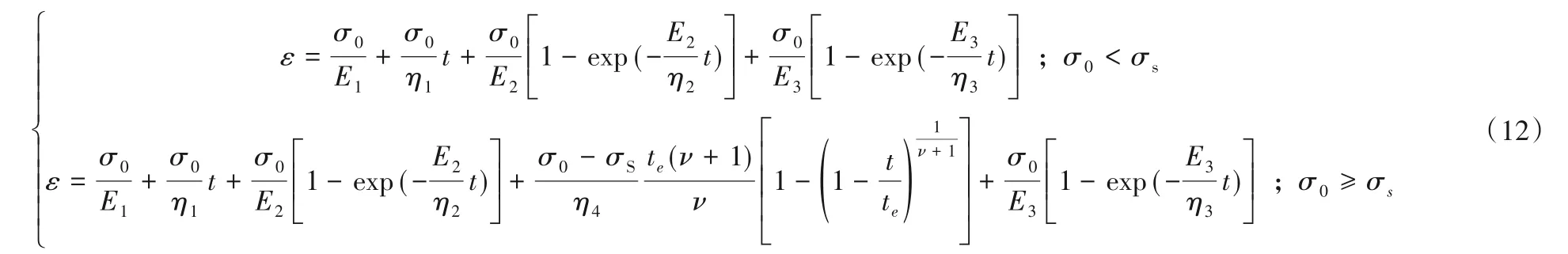
式中：σ0为初始应力；σs为长期强度。

式（12）即为本文所建一维条件下的蠕变损伤模型。

1.4 三维蠕变损伤本构模型

在岩体工程中，岩石多处于三向应力状态，由此需构建三维条件下的蠕变本构模型。假设岩石各向同性，依据广义Hooke定律有：

式中：σm为球应力张量；Sij为偏应力张量；K为体积模量；G为剪切模量。

分解岩石内部的应力张量，于是有：

式中：σij为应力张量；δij为单位张量。

一般认为，岩石在三维应力下不发生体积蠕变［13］，故本文三维蠕变方程中不考虑体积蠕变，并引入屈服函数F来描述岩石的屈服。由此将式（12）推广为三维应力状态：

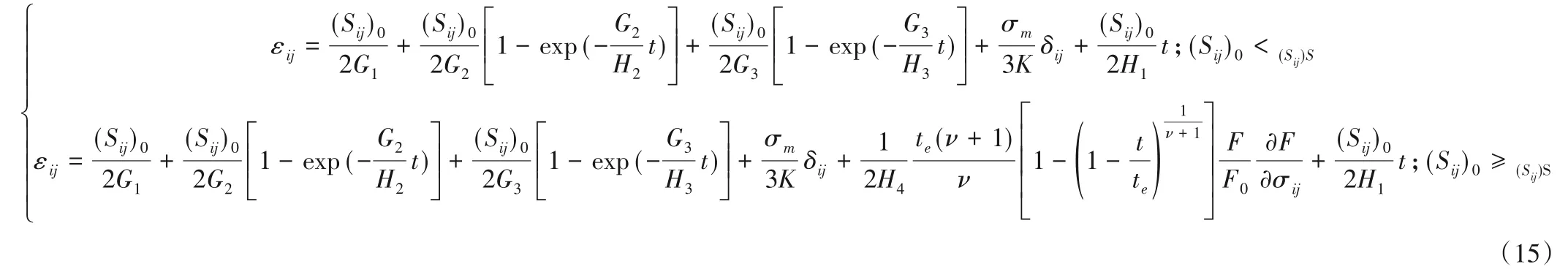
式中：（Sij）0为初始偏应力张量；（Sij）S为对应长期强度的偏应力张量；G1、G2和G3为对应E1、E2和E3的剪切模量；H1、H2、H3和H4为三维黏滞系数；F0为屈服函数的初始值。

屈服函数可以取如下形式［13］：

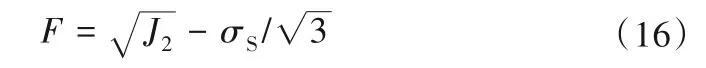
式中：J2为应力偏量第二不变量。

在等围压三轴压缩应力状态中有：

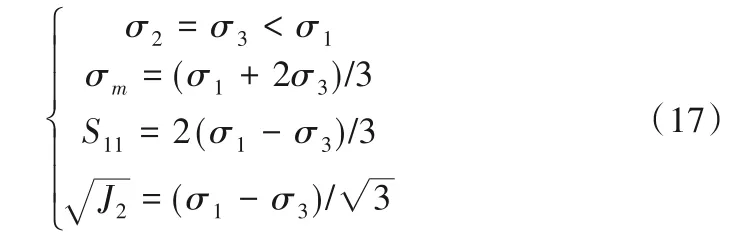
将式（17）代入式（15）可得：

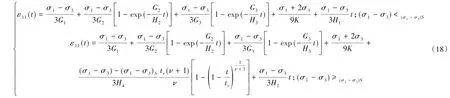
式（18）即为本文所建三维岩石蠕变损伤模型的轴向蠕变方程。

2 模型可行性验证及参数求解

2.1 岩石蠕变试验

试样取自某水电工程边坡平硐内页岩岩层，运回实验室后制备成直径50 mm、高100 mm 的圆柱样。蠕变试验采用RLW-2000 型岩石三轴流变试验系统，将围压分别设置为1、2 和3 MPa，共施加5级轴向荷载。通过试验数据采集系统，得到3种围压下的分级加载蠕变曲线（偏应力标示在曲线上），如图4所示。

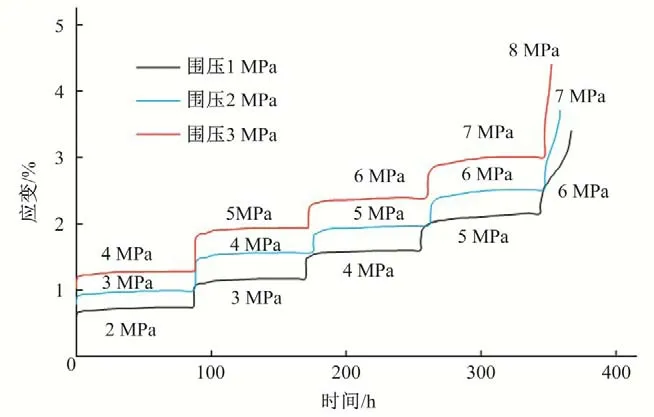
图4 分级加载蠕变曲线Fig.4 Creep curves under step loading

由图4可看出，岩石在应力作用下首先出现瞬时弹性变形，接着进入衰减蠕变阶段，该阶段蠕变速率递减，当蠕变速率衰减到某一恒定值附近时，便进入了稳定蠕变阶段，当应力加载到某一级别时，岩石还表现出历时较短的加速蠕变，随后岩石破坏。总体上，随着围压的提升，对应级别的应变量值递增。由于式（18）针对每一级加载，故还需根据玻尔兹曼原理［7，8］对图4进行处理，得到分别加载蠕变曲线，从而对每一级加载的蠕变曲线进行拟合辨识。

2.2 参数求解

（1）参数G1和K。根据广义Hooke定律有。

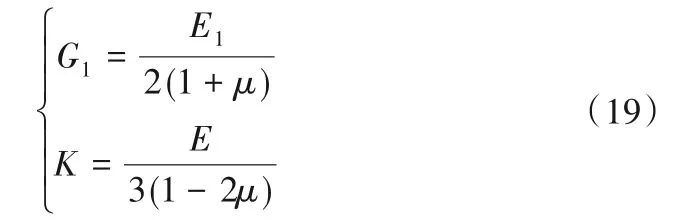
式中：μ为泊松比。

根据等围压三轴压缩试验可求得E1和μ，从而确定G1和K，限于篇幅，这里不再给出等围压三轴压缩试验结果曲线。

（2）参数G2、G3、H1、H2和H3。岩石蠕变试验前4 级加载中，未出现加速蠕变阶段，通过式（18）的第一式求取参数，通过数学软件Origin，基于Levenberg-Marquardt 算法，进行非线性拟合便可确定参数G2、G3、H1、H2和H3。

（3）参数H4、te、ν和长期强度（σ1-σ3）s。当岩石外界应力水平超过长期强度时，还会表现出加速蠕变阶段。采用式（18）的第二式求取参数H4和ν，根据试验总历时确定蠕变破坏时间te，根据等时应力-应变曲线法［20］确定长期强度，三种围压下的长期强度分别为4.75、5.68 和6.64 MPa，限于篇幅，这里不再给出求取过程。

2.3 页岩蠕变模拟

通过式（18）辨识页岩分别加载蠕变曲线，同时利用传统三维Burgers 模型作为对比验证，得到理论值与试验值对比曲线，如图5所示。模型参数如表1所列。

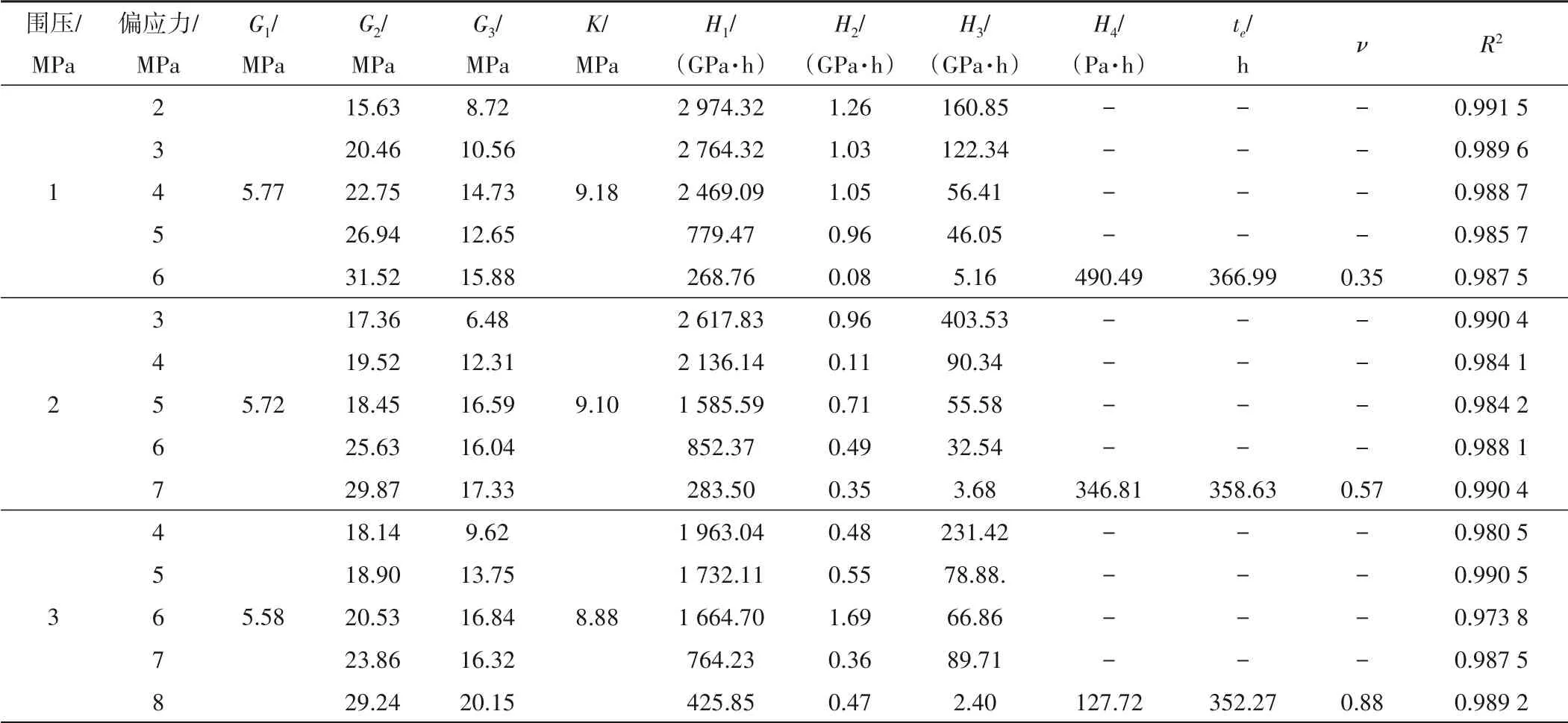
表1 模型参数Tab.1 Parameters of model

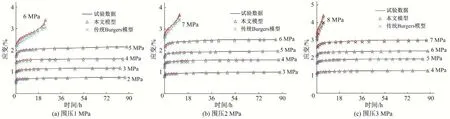
图5 理论值与试验值对比曲线Fig.5 Comparison curves between theoretical value and experimental value

由图5 和表1 可看出，本文所建模型对页岩蠕变试验数据拟合效果较好，平均R2达到了0.986 8。传统三维Burgers 模型的平均R2仅有0.926 4，对前4 级蠕变数据拟合误差相对较小，但拟合值始终略低于试验值，无法辨识最后一级蠕变数据，难以描述岩石加速蠕变阶段。

3 参数分析及适用性验证

3.1 参数敏感性分析

为了研究材料参数ν对岩石蠕变发展的影响，判断其敏感性，将不同ν值和表1 中剩余已确定模型参数代入式（18），以页岩围压1 MPa 下最后一级应力水平为例，绘制不同ν值的蠕变曲线，如图6（a）所示。以同样的方法绘制不同H4值的蠕变曲线，如图6（b）所示。

图6（a）中ν=0.35 时的蠕变曲线即为图5（a）中最后一级理论值曲线，当ν值逐渐增加时，蠕变曲线逐渐远离时间轴，曲线斜率递增。材料参数ν影响蠕变速率和极限蠕变值，ν值的变化明显影响曲线形态。当ν值从0.25 增长至1.00 时，ν值增长了300%，应变值从0.032 4 增加至0.061 9，应变值增加了91.05%，ν值平均每1%的变化引起了应变值0.30%的变化。

由图6（b）可知，应变值随着H4值的减小而递增，黏滞系数H4值影响蠕变速率和极限蠕变值，同时影响曲线形态。当H4值从300 GPa·h 增长至700 GPa·h 时，H4值增长了133.33%，应变值从0.045 5 减小至0.031 2，应变值减少了31.43%。H4值平均每1%的变化引起了应变值0.24%的变化，与ν值对比发现，材料参数ν的敏感性高于黏塑性体的黏滞系数H4。

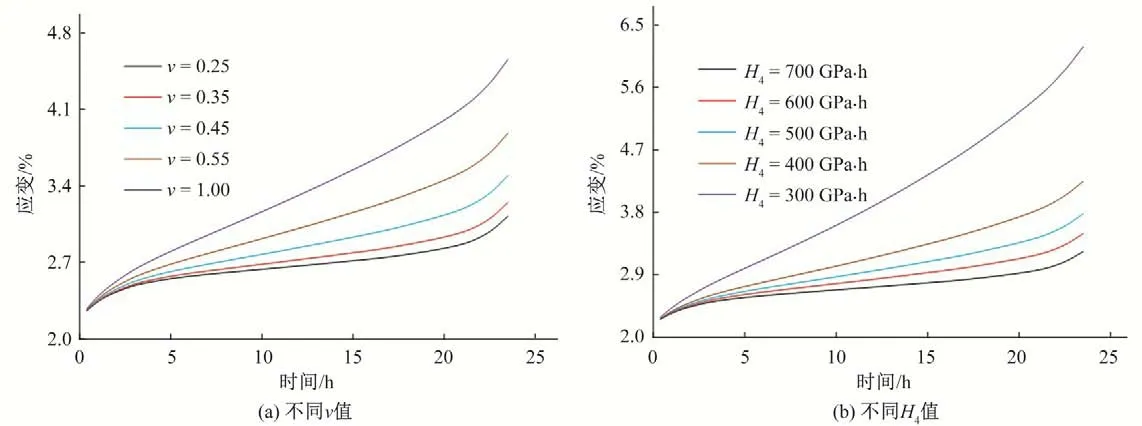
图6 不同参数值的蠕变曲线Fig.6 Creep curves with different parameters

3.2 模型适用性验证

岩石按照坚硬程度将岩石划分为坚硬岩、较硬岩、较软岩、软岩和极软岩［21］，本文蠕变试验对象页岩属于软岩。为了验证本文所建模型描述不同类型、不同硬度岩石蠕变力学行为的适用性，引用文献［22-25］中的石英砂岩、板岩、凝灰岩和全风化花岗岩的蠕变试验数据，通过本文所建模型进行拟合。由于Burgers模型无法描述岩石加速蠕变阶段，引用文献［26］中可反映加速蠕变过程黏塑性变形的三维Cvisc 模型进行对比验证，得到理论值与试验值对比曲线，如图7所示。

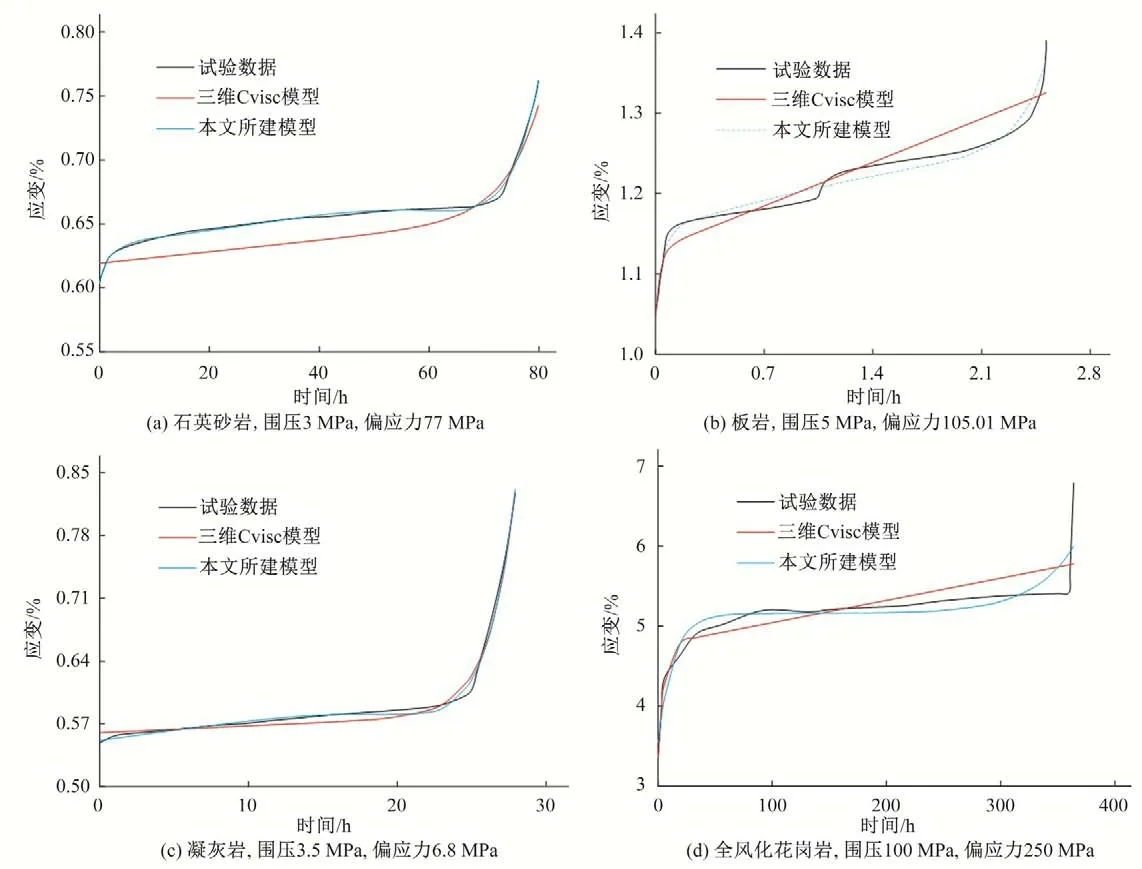
图7 理论值与试验值对比曲线Fig.7 Comparison curves between theoretical value and experimental value

分析图7，利用三维Cvisc 模型辨识4 种岩石的R2分别为0.928 9、0.902 4、0.983 3 和0.881 7，本文所建模型辨识4 种岩石的R2分别为0.997 3、0.975 2、0.991 6 和0.953 8。石英砂岩、板岩、凝灰岩和全风化花岗岩分别属于坚硬岩、较硬岩、较软岩和极软岩［21］，由于不同类型、不同硬度岩石的蠕变曲线形态各异，尽管三维Cvisc 模型拟合凝灰岩蠕变数据时具备较好的模拟能力，但对石英砂岩、板岩和全风化花岗岩的拟合效果较差，适用范围较小。本文所建模型总体上拟合精度更高，能较好地识别5 种坚硬程度岩石的蠕变力学行为，由此证明本文所建蠕变损伤本构模型反映不同类型岩石蠕变特性的适用性。

4 结论

（1）根据岩石蠕变黏弹塑性变形特性，选择广义Burgers 模型作为基础模型，引入损伤力学理论，引入损伤力学理论，建立考虑时效损伤的黏塑性体，与基础模型串联，得到新的考虑时效损伤的岩石黏弹塑性蠕变本构模型，并推广至三维应力状态。

（2）利用所建模型辨识页岩蠕变试验数据，给出参数求解办法，并进行参数敏感性分析，材料参数ν的敏感性高于黏塑性体的黏滞系数H4。对比试验曲线和理论曲线，证明所建模型的可行性和合理性。

（3）引用相关文献中不同坚硬程度的岩石蠕变试验数据，利用所建模型和三维Cvisc 模型进行拟合对比，证明了本文所建模型反映不同类型、硬度岩石蠕变力学行为的优越性，从而验证所建考虑时效损伤的岩石黏弹塑性模型的适用性。目前多数模型难以反映不同岩石加速蠕变特性，所建模型通过验证可描述不同类型、硬度岩石蠕变行为，对不同加速蠕变曲线仍有良好辨识能力，具有较广阔的工程应用前景。□