基于GIS 与随机森林算法的斜坡单元类型划分方法

刘 彬

（广东省测绘产品质量监督检验中心，广东 广州 510075）

0.引言

斜坡单元是地震、泥石流等斜坡地质灾害发育过程中最重要的衡量指标，因此可以通过探究斜坡单元的类型，衡量一片区域地质灾害发生的机理、规律，并进行预测分析。在地理信息技术被广泛应用于地质结构、地理观测等学科之后，通过GIS进行地质表面的结构分析已经是一种十分普遍的行为。将斜坡单元类型的划分应用在GIS中，是一个十分复杂的问题，现有的几种划分方法都不是很准确。

文献[1]通过地理信息系统的应用，切割了斜坡单元周边存在的界限，并基于纹理分水岭划分了斜坡单元的分割依据，并经过预处理的DEM图像，以灰度矩阵的方式，对分水岭的坡度进行了标记，使其能够将正负地形中的分水岭被准确划分。这种方法相对于其他方法拥有更好的切割效果，但是在坡度的计算上准确度较差。文献[2]通过敏感性评价获取了地势起伏的最佳提取单元，以均点算法计算了坡度的起伏均值，并获取了平均峰值的分布关系。在不同的网格中计算了坡度提取的最佳面积。这种方法着重分析坡度起伏与峰值的关系，对沟谷斜坡密度的计算帮助不大。文献[3]利用DEM坡度图像计算出来同一单元下的数据精度，并通过Python ArcPy程序获取了最佳统计单元的计算方法。在此过程中需要通过空间计算的方式，因此内存占用较大，运算时间较长，运算结果的准确度也不理想。综合以上文献，本文设计了一种以随机森林算法为核心的GIS斜坡单元类型划分方法，通过实时更新斜坡单元倾角度数，通过GIS划定了斜坡单元分类标准，并通过随机森林优化了斜坡单元划分算法。

1.基于GIS 与随机森林算法设计斜坡单元类型划分方法

1.1 更新斜坡单元倾向角度

在计算斜坡的坡向剖面时，可以通过坡体底部水流的方向，获取该单元内斜坡的倾向计算方法。在最小二乘法下[4]。每一个拟合的数据都可以用来计算斜坡单元，其高程可以简略地看作一种以内部坐标为基准的线性函数，如公式（1）所示：

式（1）中，Td为该DEM图像中，斜坡单元的内部高程数据；x和y则为斜坡单元拟合数据的内部坐标；ηn、λn、δn均为常数。将以上斜坡单元的线性方程带入到DEM数据中，可以得到一个单元倾向的三维立体角度，（如图1所示）：

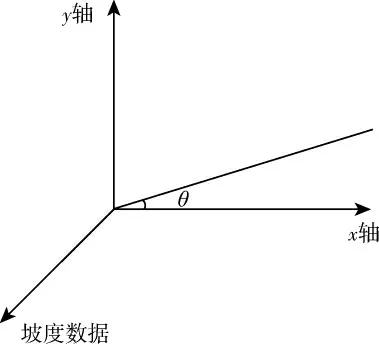
图1 单元倾向角度

图1中，坡度高程数据通过拟合计算带入到x轴和y轴中，可以得到一个夹在x轴和y轴之间的角，这个角θ就是坡度单元倾角。通过求导计算，可以得到该平面的倾向坐标，如公式（2）所示：

式（2）中，ai和bi分别为坡度平面单元倾角的两个方向参数；xd和yd则为x轴与y轴平面上的两个单位向量坐标刻度。则结合ai和bi，该倾角判定计算如公式（3）所示：

式（3）中，θn为在第n个斜坡单元中倾角角度；ai和bi的意义如上。将高程及其相关的变量关系构成一个整体性的系统，如公式（4）所示：

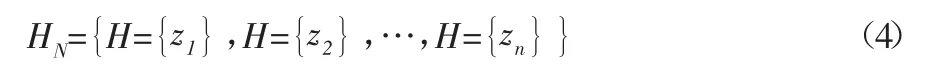
式（4）中，HN为在GIS中经过形态局部变量可以改变高程的元素集合；z1、z2、…、zn分别为集合中的第1个、第2个、…、第n个元素。通过近似坐标估计，可以直接得到斜坡单元倾向的更新坐标，如公式（5）所示：

式（5）中，ak和bk分别为更新后的斜坡单元倾向坐标；hk为观测数据的第k个节点；uk为三维估计的环境质点为坐标估计的近似值。结合以上公式，带入到公式（3）中，可以直接求出斜坡单元倾向的实时角度。

1.2 基于GIS生成斜坡坡度矢量图层

在GIS中生成斜坡坡度矢量图层时，首先需要计算平均曲率，此过程不需要通过剖面曲率的计算，只需要计算其斜坡分割面积，并通过坡面的侵蚀划定地表的局部发育粗糙度[5]。在凸出的地形元素边界，可以通过划定极大值或极小值的方式验证分水岭的地表倾斜角度，然后去除高程中的尺度变化，使其可以适当增加均值的滤装置。通过划定可行域的方式，建立一个栅格化的目标质点，然后通过多边形顶点的内部结构，判定线段方程的角度与连线中心[6]。尤其是在计算随机误差时，通过最小二乘法获取最优解是最简单的方式。如果斜坡被外力破坏，则需要通过内外力之差计算不平衡比率的初始应力。在计算中，通过收敛速度的快慢、收敛过程的波动特性以及不平衡力的比率条件，可以直接完成模型中的坍塌或塑形过程，利用GIS的筛选功能，可以直接删除缓冲区分析中的叠置影像，并生成一个矢量图层，作为该类型图的属性统计标准。所有位置坐标中斜坡高程的计算都可以通过DEM模型中坡向和坡度的提取和计算，在研究区的原始图像内生成一个具备重分类效果的坡度矢量图层。

1.3 基于随机森林优化斜坡单元类型划分算法

随机森林算法，可以通过大量的决策树构建向量模型，并通过这些模型得到随机分布的决策向量，是每一棵树都进行斜坡单元分类标准的投票，通过统计这些投票数量，获取不同的类型划分信息。在随机森林算法的回归模型中，可以通过梳理分析进行独立变量的条件统计，并利用回归函数确定独立变量的概率分布空间，使随机分布的变量X和独立变量Y联合在一起，设定多变的条件概率，从而获取回归函数的预测数据。通过原始标记中的样本，可以将每一个节点的分类作为叶结点的存储信息，这一类数据需要拥有两种必要条件，分别是：可以实时更新数据样本、可以分裂子节点中的规则密度。这样一来，通过随机森林算法就可以得到概率的回归分析模型，如果调整了随机森林的结构，就可以直接优化随机森林中的斜坡单元划分算法。在机器领域，这个预测数据是十分具有代表性的，本文通过这组回归数据，假设了训练集的分布规律，将其与预测器联合在一起，划定了分类标准，由于预测之中有很多分类器的平均值，可以通过随机误差变量的边缘函数来计算随机树的总量，如公式（6）所示：

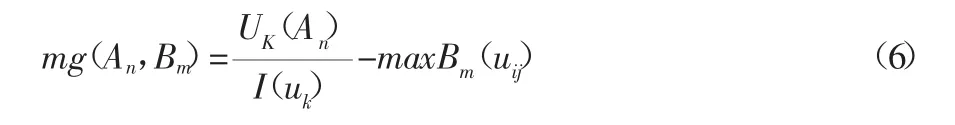
式（6）中，mg（An，Bm）为两棵随机树An、Bm的均方误差；UK（An）为随机向量An被分到正确票数的概率；Bm（uij）为在事件中随机向量Bm备份到正确票数的概率；I（uk）为指示函数的平均值。在求解边缘函数的过程中，可以通过构建回归分析的预测数据，计算线性回归的最小二乘法，将其与预测数值匹配，可以得到泛化的误差分析。在斜坡单元类型划分标准的构建中，通过随机森林算法可以直接提取影像的基本特征信息，由于每一个图像在细化到栅格中都具备极大地差别，因此其在应对光暗对比、影响旋转重叠等方面都具备极大地逻辑性，并具备一定的特征变换规律。可以通过建立已知信号的方式定义这种函数，如公式（7）所示：

式（7）中，an为斜坡单元类型划分过程中的第n个变换方向。在计算梯度值时，可以通过公式（8）设定图像的原始文本。

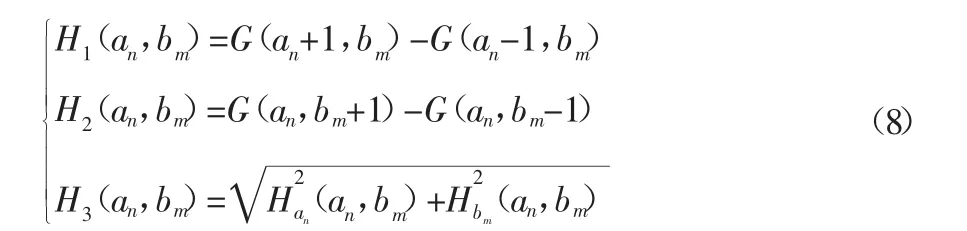
式（8）中，H1（an，bm）、H2（an，bm）、H3（an，bm）分别为在三种类型的像素中，水平梯度的变化规律；an和bm为x轴与y轴上的两个坐标点；Hbm为在垂直方向上像素点的坐标梯度；Han为在平行方向上，像素点的坐标梯度。结合以上公式，可以直接得到随机森林分类的路径（如图2所示）：

图2中，左边的树状图案是第一棵树中的节点，右边的树状图案是第n棵树中的节点。在分类的过程中，通过样本概率分类器计算第一棵树中的属性判定条件，可以通过公式（9）来计算：

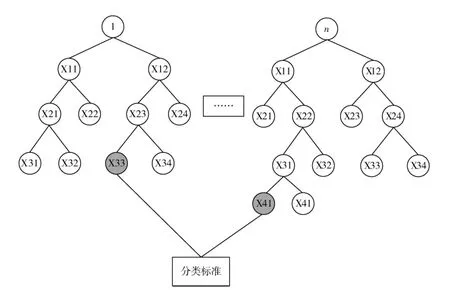
图2 随机森林算法分类路径

式（9）中，KH为位置类别的样本在划分坡度类型时斜坡单元类型划分的标准路径长度；ki为在第i个节点中的第一棵树的参数子集；xi为在第i个节点中的最后一颗树的参数子集。通过以上算法可以提高斜坡单元类型划分算法中斜坡密度的精确度，从而实现对划分方法的优化。

2.实验研究

2.1 实验准备

本文设计了一个斜坡单元类型划分的方法，将其与基于纹理分水岭的算法、尺度提取算法、利用Python ArcPy的地形最佳算法相对比，分别检测当沟谷斜坡密度的计算值与实际测量值相等时集水面积阈值的数值，将实验数据作为判断四种斜坡单元类型划分优劣的标准。通过ArcGIS进行卫星地图的编辑与分析，选取某市山区的地形图（如图3所示）：

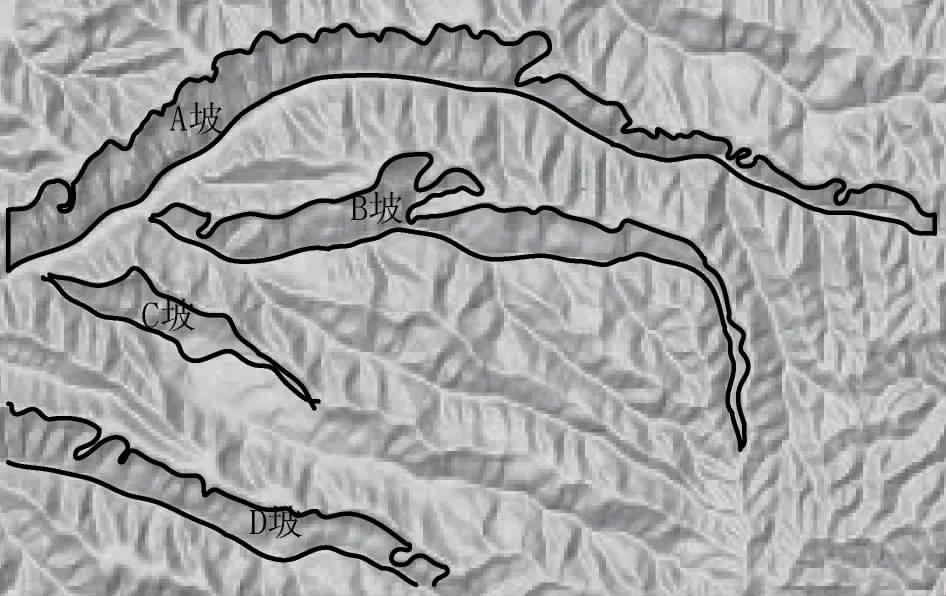
图3 沟谷斜坡勾绘

图3中，该卫星地图中斜坡资源十分丰富，为了得到更准确，更具代表性的实验数据，在图3中选择了四个高度不一的沟谷斜坡。其中，A坡的绝对高度为23.6m，B坡的绝对高度为30.8m，C坡的绝对高度为11.4m，D坡的绝对高度为14.6m。在ArcGIS上通过（如图4所示）的流程提取坡面单元。

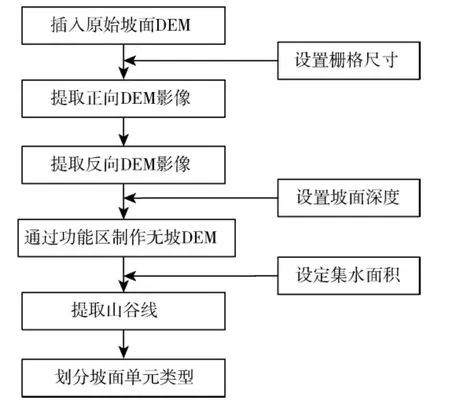
图4 提取坡面单元流程

在ArcGIS中建立一个坡面单元数据集，作为影像处理与记录的集合，设定初始坡面DEM的栅格尺寸为300m，通过“功能”模块提取正向与反向的坡面DEM影像，将提取得到的影像全部保存在数据集中。选择四个不同深度的坡面A、B、C、D，将其通过线条勾绘成单独的矢量模型。然后在设置坡面深度，从而提取无坡面的DEM影像，将无坡面DEM同样存储在数据集中。通过缓冲区叠加分析工具，结合集水面积数值，计算山谷线走向，并通过“工具”菜单得到山谷线的线形矢量图层。在计算不同集水面积阈值下的斜坡密度时，可以通过最小二乘法的观测最优估计来进行判定，如公式（10）所示：

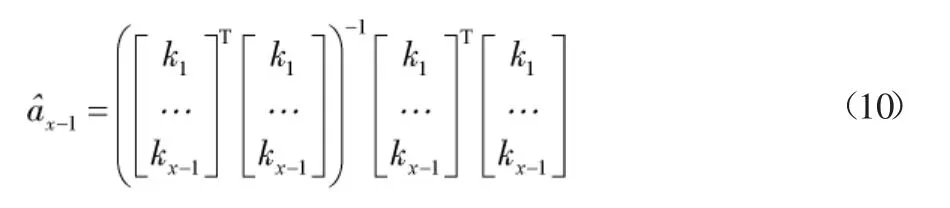
式（10）中，ax-1为通过最小二乘法获得的最优观测估计；k1、kx-1分别为集合中第1个和第x-1个观测对象。通过该最小二乘矩阵方程，可以得到最新的观测数据，如公式（11）所示：

式（11）中，hx为环境感知质点中通过三维压缩得到的单独观测数据；xi为第i个观测点的维度特性，也可以标示为正地形下的斜坡密度。更新观测对象，将其置换成负地形下的斜坡密度，如公式（12）所示：

式（12）中，各项参数如上。通过公式（11）和公式（12）可以得到不同集水面积阈值下沟谷斜坡的密度变化。

2.2 集水面积阈值测试

在通过四种方法计算沟谷斜坡密度前，首先需要通过实地勘测的方式得到单位面积内沟谷的长度，即沟谷密度的实际测量值。然后使用以上四种方法计算不同集水面积阈值下的沟谷斜坡密度，当集水面积阈值较小时，沟谷斜坡密度的计算值与实际测量值通常存在一定的差距，随着集水面积阈值的增长，二者之间的误差会逐渐减小。在该实验中，通过记录计算值与实际测量值重叠时，集水面积阈值的数值大小，判断该方法的有效性和优越性。集水面积阈值越小，则该方法斜坡类型划分的准确性越高。将通过以上实验得到的数据结果（如图5所示）：

在图5的四幅图像中，当集水面积阈值小于300时，四种方法计算得到的沟谷斜坡密度均没有与实际测量值相等。在斜坡A中，使用随机森林算法得到的沟谷斜坡密度，在集水面积阈值为700时，与实际测量值相等。使用纹理分水岭算法则是在集水面积阈值为900时得到与实际测量值相等的计算值，尺度提取算法和Python ArcPy的最终结果也为900。在斜坡B中，文中方法的数值为500，其他三种算法的数值分别为700、700、1100。斜坡C坡度较小，导致实验中的整体数值较小，在四种方法下的数值分别为500、700、700、700。斜坡D的四项数值分别为500、900、700、1100。综合以上实验数据，在四种斜坡单元类型划分方法的计算中，使用文中方法可以减小集水面积阈值的设定值，并提高单元类型划分的准确性。

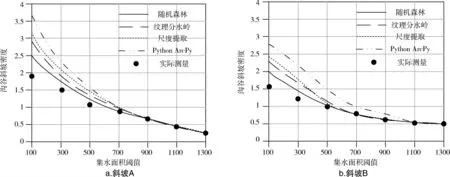
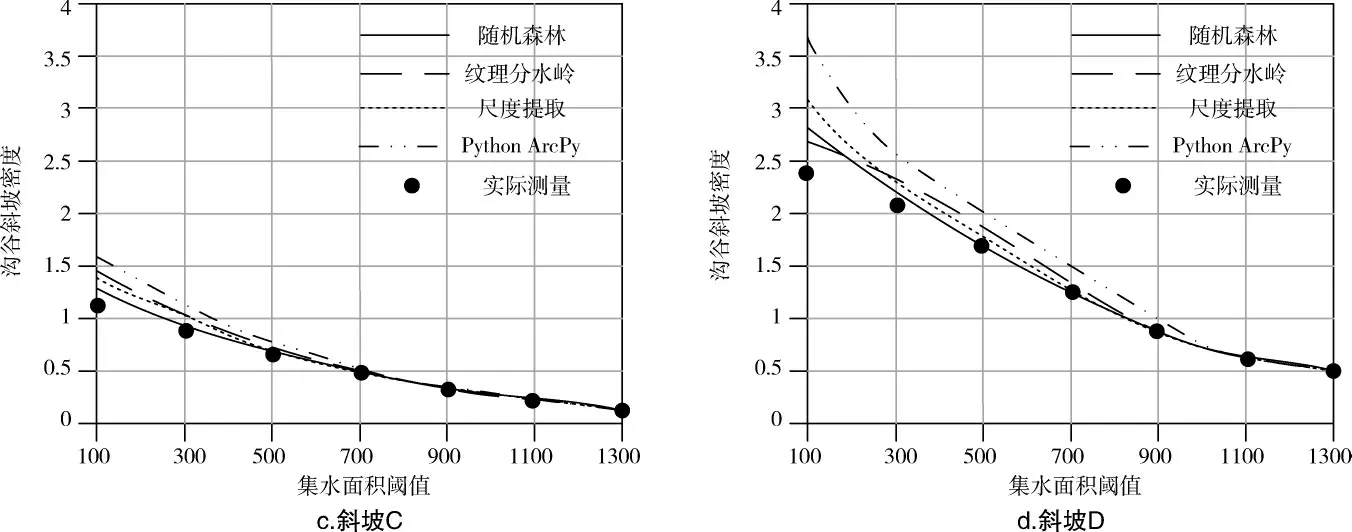
图5 集水面积阈值测试

3.结束语

通过ArcGIS与随机森林算法设计了一种斜坡单元类型的划分方法，然后通过算法的优化，提高了沟谷斜坡密度计算值的准确度，使其能够在更小的集水面积阈值中拥有与实际测量值相吻合的数据。又通过实验与现有的三种算法进行对比，验证了该算法的有效性和优越性。通过该研究成果，可以提高斜坡地质稳定预测的精准性，具备一定的推广价值。