高中数学解题中导数的应用
2021-09-27曾志超
曾志超
(江西省赣州市南康区第三中学 341400)
高中数学导数部分既可以单独命题,也可以与其他知识点结合起来进行命题.教学中为提高学生运用导数解题的灵活性,为其数学学习成绩的提升奠定基础,不仅要为学生认真讲解导数的基础知识,而且应通过讲解导数的应用,引导学生总结相关的应用技巧,使其在以后的解题中少走弯路.
一、用于解答数列问题

A.-38 B.38 C.-17 D.17
分析题目给出的a6和a8为函数f(x)的极值点,因此,需要先求出a6和a8,并根据公差d>0,求出a1的值,运用等差数列前n项和公式求S8的值.
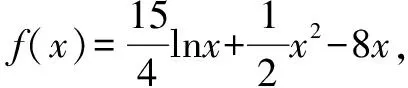
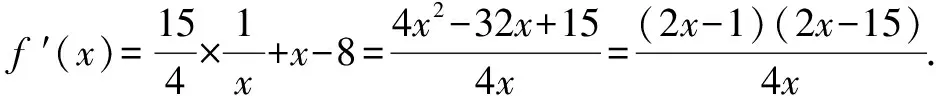
因此,函数的极值在f′(x)=0处取得.


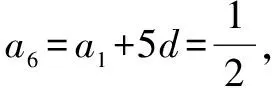

点评运用导数解答数列问题应结合已知条件,寻找数列项与函数极值之间的关系,尤其应注意函数在其导数为零处取得极值,如此便可很好地突破.同时,在判断数列项的大小时还应注重结合已知条件.
二、用于解答函数问题

A.1 B.2 C.3 D.4


因两条直线和y轴分别交于A,B两点,则容易求得A(0,1-lnx1),B(0,lnx2-1).则|AB|=|2-ln(x1x2)|.
点评运用导数解答函数问题应深刻理解导数表示的几何含义,尤其在求解函数图象上某一点的切线时应注重合理设出参数,运用导数知识写出切线方程,而后再利用已知条件找到参数之间的关系.
三、用于解答不等式问题
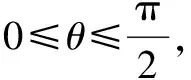

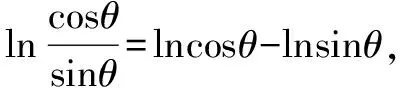
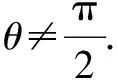

点评一些不等式习题难度较大,应注重认真观察给出的已知条件,通过对已知条件进行合理转化,构造出对应的函数,并注重运用导数知识研究构造函数的相关性质,实现顺利解题的目标.
四、用于解答方程问题
例4 已知实数a,b分别满足方程lnx+x-2=0,ex+x-2=0,则函数y=xln|x|+a+b的极大值为( ).
分析因为lnx+x-2=0,ex+x-2=0,所以lnx=2-x,ex=2-x.又因为y=lnx和y=ex互为反函数,图象关于y=x对称,则将y=x和y=2-x联立,解得x=y=1.
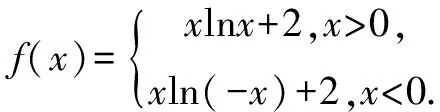
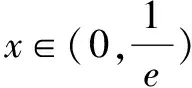

点评运用导数解答方程类的问题时应注重积极联系所学,通过转化求解出相关参数,运用导数知识通过探讨函数性质进行解答,尤其在研究分段函数性质时应注重在其定义域内进行探讨.
导数涉及很多的基础知识,主要有导数的定义、导数的几何意义以及各类函数的求导公式等,只有牢固掌握这些基础知识,才能在解题中灵活应用,因此在讲解基础知识时应注重灵活运用多种教学方法激发学生的学习兴趣,深化学生对导数知识的理解.同时,注重在课堂上优选精讲典型习题,使学生掌握不同题型的突破思路以及应用导数解题时的细节,促进其导数应用水平的明显提升.
