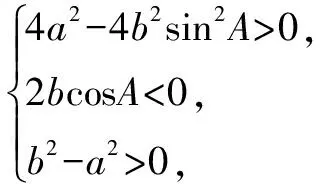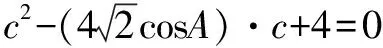判断三角形解的个数有妙招
2021-09-27廖永福
廖永福
(福建省厦门第二中学 361009)
解三角形有四种基本题型:(1)已知两边和它们的夹角;(2)已知三边;(3)已知两角和任一边;(4)已知两边和其中一边的对角.根据全等三角形的判定方法可知,前三种基本题型,三角形都有唯一解,最后一种题型,三角形可能无解、一个解或两个解.由于解的个数不易确定,因而成为教学的难点.笔者经过精心研究,归纳整理出判断三角形解的个数的四个妙招.
一、性质法
我们知道,三角形有许多性质,如“在△ABC中,A>B⟺a>b⟺sinA>sinB”“若α是三角形的内角,则0 例1 在△ABC中,角A,B,C的对边分别为a,b,c,满足以下条件的三角形解的个数为1的是( ). A.a=22,b=25,A=120° B.a=9,c=10,A=30° C.a=6,b=8,A=60° D.a=11,b=6,A=45° 分析从已知条件出发,利用正弦定理、大边对大角以及正弦函数的有界性,判断各个选项中三角形的个数,从而得出结论. 解析对于选项A,因为b>a,所以B>120°.所以满足题意的三角形不存在; 先根据已知条件画出三角形,再根据所画三角形的个数作出判断.三角形有几个,解就有几个. 画三角形的关键是确定三个顶点的位置,一般步骤是:(1)画角,确定第一个顶点;(2)画邻边,确定第二个顶点;(3)画对边,确定第三个顶点. 首先,分别根据三角形内角和定理和正弦定理求出另一已知边的对角的取值范围和正弦表达式;其次,构造相应的正弦函数和常数函数并画出它们的图象;最后,根据两个函数图象交点的个数作出判断, 交点有几个,三角形的解就有几个. 分析利用正弦定理,可用a表示sinA,结合C的大小,可知A∈(0°,120°).构造相应正弦函数和常数函数并画出其图象,结合存在两个三角形的条件,即可列出a满足的不等式,求得a的取值范围. 在△ABC中,已知边a,b和角A,则△ABC有几个解等价于关于边c的一元二次方程c2-(2bcosA)c+b2-a2=0(*)有几个不等的正根. 证明由余弦定理知,边c是方程(*)的根,△=(2bcosA)2-4(b2-a2) =4a2-4b2sin2A. 综上,△ABC有几个解等价于方程(*)有几个不等的正根. A.0° C.0° (*) 以上四招各有千秋,在具体的解题过程中,可以尝试用不同的方法去解同一道题,这样不仅能巩固所学的知识,而且还能更好地培养学生思维的广阔性,有利于创新意识的形成和发展.二、画图法



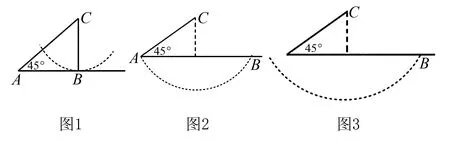
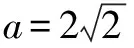
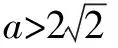
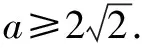
三、 图象法

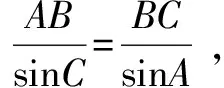
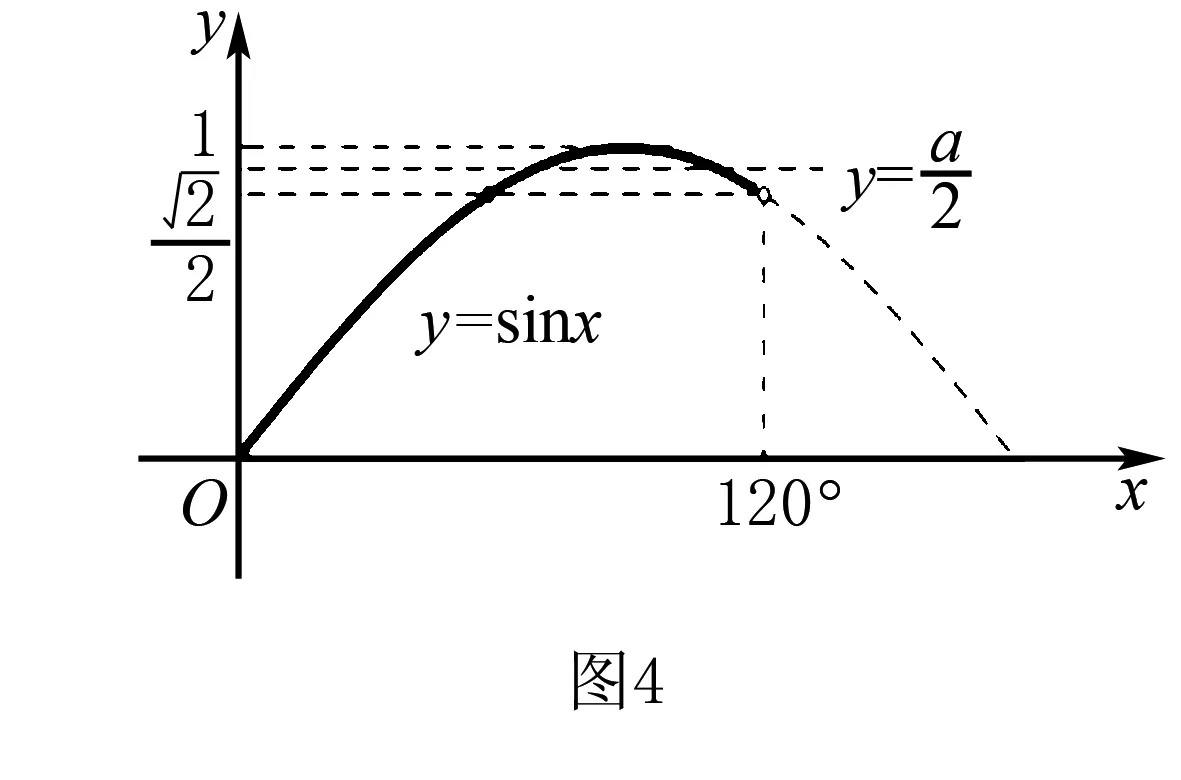
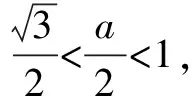
四、判别式法