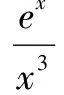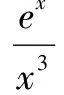同构换元法求解含指对数混合式的问题
2021-09-27杨苍洲
杨苍洲
(福建省泉州第五中学 362000)
有一类混合指对数式的函数导数压轴试题,常常可以通过指数与对数的互相转化,实现局部同构,并对同构部分的式子进行换元,从而化繁为简,并结合重要不等式进行求解,我们把此方法称为“局部同构换元法”.要掌握这种解题方法:
有了上述的两个基础知识,我们就可以应用“局部同构换元法”解决求函数的最值、不等式的证明、恒成立问题求参数等问题.
一、同构换元法求函数最值
利用重要的不等式进行放缩,是求函数最值的一种常见方法.因此,含有复杂的指对数函数问题,可以通过局部同构换元,并结合重要不等式进行放缩,把函数放缩至某常数,则该常数可能为函数的最值.此时,需注意在函数的定义域内是否存在对应的变量使得函数取得该最值.
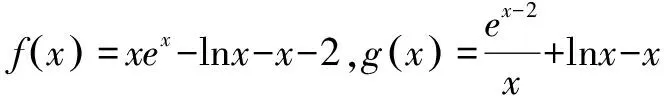
A.a=bB.a C.a>bD.a,b的大小关系不确定 解法1f(x)=xex-lnx-x-2=elnx+x-(lnx+x)-2,易知et-t≥1,当且仅当t=0时,等号成立. 所以elnx+x-(lnx+x)-2≥1-2 =-1. 所以当且仅当lnx+x=0时,f(x)取得最小值-1,即a=-1. 所以ex-lnx-2-(x-lnx-2)-2≥1-2 =-1. 所以当且仅当x-lnx-2=0时,g(x)取得最小值-1,即b=-1. 因此a=b,故选A. 解法2f(x)=xex-lnx-x-2=xex-ln(xex)-2,易知t-lnt≥1,当且仅当t=1时,等号成立. 所以xex-ln(xex)-2≥1-2=-1. 故当且仅当xex=1时,f(x)取得最小值-1,即a=-1. 因此a=b,故选A. 证明含有指对数式的不等式,可以尝试先对原不等式进行转化,从而构造出相同的式子,并进行换元,然后构造关于新元的函数,并求解含新元函数的最值,从而实现不等式的证明. 例2已知函数h(x)=(ax-1)·ex,a∈R. (1)讨论f(x)的单调性; (2)若a=1,求证:当x>-1时,h(x)≥exln(x+1)-x-1. 解法1 (1)略; (2)不等式(x-1)·ex≥exln(x+1)-x-1,等价于(x+1)·e-x-ln(x+1)+x-1≥0,等价于eln(x+1)-x-[ln(x+1)-x]-1≥0. 易知et-t-1≥0. 令t=ln(x+1)-x,故上式成立,不等式得证. 解法2 (1)略; (2)不等式(x-1)·ex≥exln(x+1)-x-1,等价于(x+1)·e-x-ln(x+1)+x-1≥0,等价于(x+1)·e-x-ln[(x+1)·e-x]-1≥0. 易知t-lnt-1≥0. 令t=(x+1)·e-x,故上式成立,不等式得证. 在含参不等式的恒成立问题中,若能构造出几个熟悉不等式的形式,那么就可以猜测参数的临界位置及其范围,并对其进行证明.如此可使得解题目标、方向更加明确. A.(-∞,1-e] B.(-∞,-3] C.(-∞,-2] D.(-∞,2-e2] ex·x-3-ln(ex·xa)-1≥0. (*) 易知t-lnt-1≥0,当且仅当t=1时,等号成立. (1)当a≤-3时,由x∈(1,+∞)知,xa≤x-3,ex·xa≤ex·x-3. 所以ex·x-3-ln(ex·xa)-1≥ex·x-3-ln(ex·x-3)-1≥0,故(*)恒成立,满足题意. (2)当a>-3时,由x∈(1,+∞)知,xa>x-3,ex·xa>ex·x-3. 所以ex·x-3-ln(ex·xa)-1 又因为当x=x0时,ex·x-3-ln(ex·x-3)-1=0,此时ex·x-3-ln(ex·xa)-1<0,不满足题意. 综上,a≤-3. (*) 易知et-t-1≥0,当且仅当t=1时,等号成立. 令t=x-3lnx,则ex-3lnx-(x-3lnx)-1≥0,当且仅当x=x0(其中x0满足x0-3lnx0=1)时,等号成立. (1)当a≤-3时,由x∈(1,+∞)知,lnx>0,alnx≤-3lnx,x-3lnx≥x+alnx. 所以ex-3lnx-(x+alnx)-1≥ex-3lnx-(x-3lnx)-1≥0,故(*)恒成立,满足题意. (2)当a>-3时,由x∈(1,+∞)知,lnx>0,alnx>-3lnx,x-3lnx 所以ex-3lnx-(x+alnx)-1 又因为当x=x0时,ex-3lnx-(x-3lnx)-1=0,此时ex-3lnx-(x+alnx)-1<0,不满足题意. 综上,a≤-3. 由上述三例可知,此方法的应用:一在于如何进行适当的恒等变形,从而得到相同的式子;二在于心中要有几个重要的不等式及其变式.此方法的应用一般都可以有两条途径,即,若能利用不等式t-lnt-1≥0解题,也应该能利用不等式et-t-1≥0解题.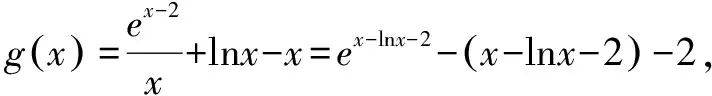

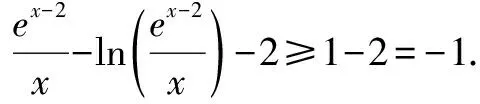
二、同构换元法证明不等式
三、同构换元法求参数范围