破解含参不等式恒成立问题的常见策略
2021-09-27许万成
许万成
(江苏省建湖县第二中学 224700)
不等式在实际生活中的应用非常广泛,因此它是历年高考考查的重点与热点,经常与其它数学知识比如函数、方程、解析几何等综合起来考查.在这类问题的考查中,同学们对于含参的问题处理起来都是比较头疼的,针对这种情况,笔者总结了三种常见的处理策略,现在以例题的形式呈现给同学们.
一、判别式法
有关含参数的一元二次不等式问题,若能把不等式转化成一元二次函数或者一元二次方程,通过根的判别式或者数形结合思想,可以使得问题得到顺利解决.
例1 对于x∈R,不等式x2-2x+3-m≥0恒成立,求实数m的取值范围.
思维点拨不等式x2-2x+3-m≥0对于一切实数恒成立等价于对应二次函数的图象恒在x轴的上方.
解析不妨设y=x2-2x+3-m,其函数图象是开口向上的抛物线,为了使y≥0(x∈R)恒成立,只需对应方程的Δ≤0,即(-2)2-4(3-m)≤0.
解得m≤2,故实数m的取值范围为(-∞,2]
评注对于在一切实数上恒成立的一元二次不等式问题,可以转化为对应二次函数图象的分布,利用判别式进行快速求解.
二、分离变量法
如果能够将参数分离出来,建立明确的参数和变量x的关系,那么可以利用函数最值求解.a>y恒成立⟺a>ymax,a 例2 已知函数y=x2-ax(a∈R)在x∈[1,+∞)时,y≥-x2-2恒成立,求a的取值范围. 故所求a的取值范围是(-∞,4]. 评注在二元不等式中,如果可以很容易地将参数与变量分离开来构造出两个函数,将求参数范围问题转化为求最值问题来处理,那么我们经常使用分离变量法来处理有关参数问题. 在有几个变量问题中,常有一个变元处于主要地位,我们称之为主元.在解含参不等式时,有时若能够换个角度,变参数为主元,可以得到意想不到的效果,使得问题可以快速解决. 例3 不等式t2-at≥0对所有的a∈[-1,1]都成立,则t的取值范围是____. 思维点拨看作关于a的一次函数,根据一次函数恒成立问题列出不等式组,求得t的范围. 故答案为:(-∞,-1]∪{0}∪[1,+∞). 评注在含参数不等式恒成立的问题中,参数和未知数是相互制约、相互依赖的关系.本题已知参数a的取值范围,求t的取值范围,若能够转换两者中的地位,则关于t的不等式就转化为关于a的不等式,问题既可以迎刃而解了.

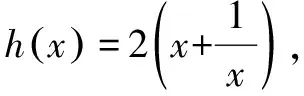
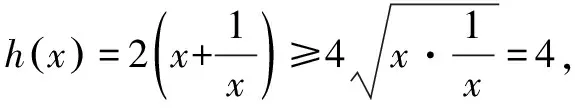
三、变更主元法

