“大道至简”：一道高考试题的解法思维层次分析

周如俊

(江苏省灌南中等专业学校 222500)

圆锥曲线上直线过定点问题是近几年高考命题的热点问题.此类试题常涉及对学生数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等核心素养的考查.

(1)求E的方程；(2)证明:直线CD过定点.

一、“普法”思维——“华山不止一条道”

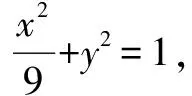
1.“直求法”——“精心运算”

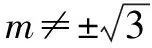
点评这种解题思维指向是设点P坐标，通过直线PA，PD与椭圆分别有两个交点特征，由韦达定理分别求出两点坐标，写出直线方程，完成定点证明.

2.“特值法”——“猜想论证”

由对称性知，直线CD所过定点必在x轴上，设定点为T(xT,0).

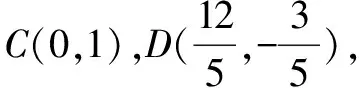
点评这种解题思维指向是从特殊情况猜想定点坐标结论，再证明猜想，体现解题思维的严谨性.

3.“代换法”——“设而不求”

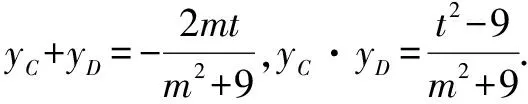
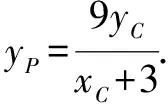
(m2+3)yCyD+m(t-3)(yC+yD)+(t-3)2=0.

点评这种解题思维指向是通过设而不求的策略，直接设直线CD方程x=my+t及C,D两点坐标，借助yC+yD,yC·yD整体代换，找到m，t满足的关系式，进而求出定点坐标.

4.“斜率法”——“对称转化”

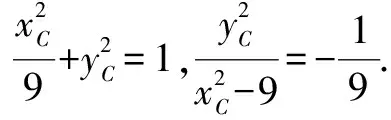
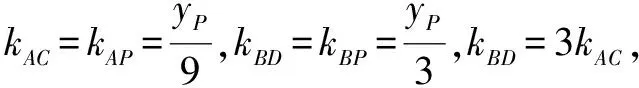
以下解法同“代换法”.

点评这种解题思维指向是利用椭圆上点与任意关于原点对称的两条连线的斜率乘积为定值的常用结论，避免了非对称式中因无法使用韦达定理解题被“卡住”的尴尬局面，体现了“对称转化”的简化策略.

5.“三角法”——“恒等变换”

由对称性知，直线CD所过定点必在x轴上.

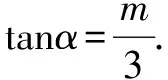
点评这种解题思维指向是利用椭圆的参数方程，引参设点求直线CD方程，借助三角恒等变换证得定点，体现了“多想少算”的优化策略.

6.“齐次法”——“平移转化”

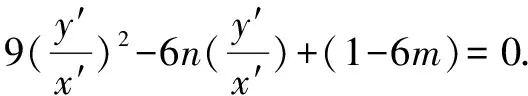
点评此解法利用过原点两条直线斜率之积为定值的简洁特性，快速求出直线mx′+ny′=1 中m，n之间关系，从而锁定定点坐标，有效降低运算的难度.

二、“通法”思维——“似曾相识燕归来”

1.“通法”化归

借鉴前述“齐次法”的研究，可将试题引申为“常态二次圆锥曲线(圆、椭圆、双曲线、抛物线)F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2≠0)上给定的点P与异于点P的动弦MN两端点之间斜率之和(之积)为定值时，求解(证)动弦过定点的问题”.

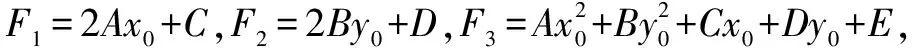
定理常态二次圆锥曲线F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2≠0)上有一定点P(x0,y0)与异于点P的动弦MN两端点.已知直线PM，PN的斜率存在，分别记为kPM，kPN.并记F1=2Ax0+C,F2=2By0+D.

若kPM+kPN=λ，则有：

若kPMkPN=λ，则有：

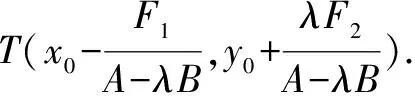
2.“通法”应用

上述定理是常态二次圆锥曲线动弦过定点(定向)问题的一类简捷、易记、便用的“通法”.

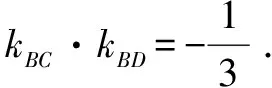
依托高考试题数据分析，是探索数学本质、关联和规律的重要研究手段，有利于增强学生基于数据表达现实问题的意识.文献大数据分析表明，2013年江西卷(理)第20题、2011年全国高中联赛第11题、2004年北京卷(理)第17题、2005年江西卷(理)第20题、2009年辽宁卷(理)第22题等高考(竞赛)试题都属于圆锥曲线上动弦过定点类问题.