网格模型的表面曲线生成方法
2021-09-27李志豪石志良
李志豪,石志良
(武汉理工大学 机电工程学院,湖北 武汉 430070)
网格模型的表面曲线是模型编辑的重要组成部分,在三维设计、网格分割、曲面几何计算、加工制造和计算机动画等领域都有所应用[1-2]。网格模型的表面曲线均要求其能够反映模型特征、具有一定美感、曲线分布均匀用以规划路径以及保持良好的平滑度。因此,研究网格模型的表面曲线生成技术,实现表面曲线的个性化编辑,具有理论和实际应用价值。
网格表面曲线的设计方法都聚焦于有特定性质的曲线,如测地线[3-4]、具有特殊曲率的曲线以及等平面曲线[5]。目前主要有参数曲线、曲线光顺以及曲线投影3种获得表面曲线的方法。在曲线参数化设计方法中,将流形曲面转换到欧式空间,使用曲线参数进行设计。韩林等[6]运用指数映射参数化的方法,提出一种离散指数映射的测地B样条曲线设计与复用方法,但这种生成方法在大规模网格区域上表现不佳。该方法通常采用单一参数化的方法,需要频繁地对参数域进行更新,同时也很少考虑到网格失真的影响。在曲线光顺方法中,首先定义初始曲线,依据不同的光顺策略对其进行平滑迭代处理。Chen等[7]提出一种优化驱动的三角网格测地路径计算方法,将目标函数表示为总长度,采用L-BFGS求解器使其最小化,解决了现有方法收敛速度慢、大规模网格模型上光顺效率不足的缺点。Jorge等[8]提出一种非线性表面曲线优化方法,该方法基于测地圆锥贝塞尔曲线的定义,代表了有理二次型下测地贝塞尔曲线在网格表面的自然扩散过程,实现了表面曲线的光顺。Kai等[9]提出一种基于测地线曲率局部约束的三角形曲面网格分段线性曲线光顺新方法,该方法使最终曲线与初始曲线保持一定的接近性。此外,用户可以调整贴近度,使用参数控制曲线的平滑过程,并通过实验验证算法的正确性与健壮性,但其受曲面的约束导致效率较低。在采用曲线投影的方法中,将定义的空间曲线进行投影映射,得到网格模型的表面曲线。Panozzo等[10]将网格嵌入到高维欧几里德空间中,通过广义加权平均和投影计算空间样条曲线,并将结果映射到曲面上,通过这种投影,曲线的平滑度得到了良好的保持。此外,Jin等[11]提出了一种基于壳空间约束的曲面网格曲线设计方法,该方法通过自适应地改变壳空间的厚度和流形能量的权重,综合了基于投影和基于平滑的方法的优点。
笔者针对网格模型表面曲线的生成方法进行研究,提出一种基于测地曲率的三角网格表面曲线生成方法。在最初定义的初始控制点上,使用最短路径确定初始曲线,通过曲率和邻域约束来逐步平滑原始曲线。这种方法控制初始曲线的平滑距离,使最终曲线与原曲线保持接近,同时避免其他方法出现的特殊顶点状态,有较高的稳定性。最后,将本文算法应用到医用外固定支具的网格模型上,结果显示,算法适应性好,能够满足工程应用的要求。
1 表面曲线的生成
1.1 算法目标及要求
表面曲线生成算法是从最初的锯齿状曲线获得光滑的表面曲线,最终应用于网格模型的切割。因此,算法的总体目标是基于初始曲线和底层曲面网格构建一条平滑曲线。通过曲线平滑,调整曲线在网格上的位置与形状,以此来获得较光滑的曲面曲线,同时还要尽可能与初始曲线接近。但是,由于初始曲线处理后形状和拓扑会发生改变,甚至超出可控范围,因此需要对平滑曲线的生成做一定要求:
(1)自适应性。在网格的局部区域上,网格拓扑较复杂,平滑曲线必须适应局部网格拓扑。因此,算法要求曲线在平滑阶段可以根据局部情况适当地改变拓扑,在保证表面曲线质量的同时保持适应性。
(2)曲面域。为便于后续的网格处理,平滑后的曲线必须位于曲面上,不能与初始曲线的形状差异过大。因此,需要对平滑范围适当控制,并且每个插入或合并的曲线点必须位于曲面上。
(3)稳健性。曲线平滑阶段需保持稳健性,避免因劣质面片和崎岖表面拓扑导致算法崩溃。
1.2 算法概述
表面曲线生成算法主要由3个部分组成:
(1)初始化。用户提供初始曲线、最终曲线的所需曲率及其到初始曲线的最大距离。
(2)平滑。在平滑过程中,曲线点在用户定义的区域内沿曲面边移动,这个过程可能需要对曲面点做局部调整,如分割和合并。
(3)求值。每个平滑步骤之后都会对曲线求值,以确定终止点并识别临界曲面顶点。这些临界顶点会限制曲线点的移动,当曲线点向这些顶点移动时,需要对其进行适当的处理。
1.3 初始化
算法的输入由初始曲线和期望曲率以及到初始曲线的最大距离组成。初始曲线由用户交互控制,用户在网格上添加控制顶点,然后由最短路径连接。该曲线是由一系列顶点线段组成,若3个相邻点位于一个三角形上,即这3个点都是该三角形的3个顶点,则进行简化操作,将这3个点的中间点删除,使第一个点直接与第三个点相连形成新的曲线段。此外,还有其他方法生成初始曲线,如基于特征的分割等方法,这种方法采用计算相邻两个面片曲率的方法,得到的曲线可以反映网格模型的特征,大多是模型上的锐边,但其灵活性较差。
图1为点pi的一环邻域,pi-1和pi+1分别为该点的上一个点与下一个点。
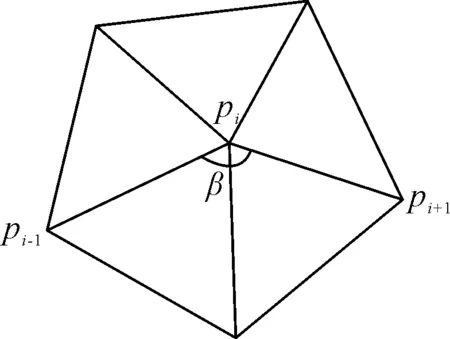
图1 点pi的一环邻域
曲线上的每个点定义的初始测地线曲率kg计算公式为:
(1)
式中:θ为该点的总角度,即以点pi为顶点的相邻三角形的角度和;β为曲线上该点的角度,即pipi-1和pipi+1的夹角。
对每个曲线点pi赋予一个期望的测地曲率kd(pi),目的是便于后续将曲线点移动到与其测地曲率相似的位置上。所需的测地曲率kd(pi)通过使用用户指定的值t在测地曲率kg和0之间执行线性插值来计算。
kd(pi)=t·kg(pi)t∈[0,1]
(2)
当t=1时,算法应返回初始曲线;t=0时,曲线为最短测地线,这种情况意味着曲线尽可能平滑,但可能与初始曲线有很大的偏差。
引入曲线点的最大移动距离约束,将曲线点的移动限制在一个允许的区域限制内,该区域由曲面上初始曲线的欧几里德距离定义。在实际应用中,使用初始曲线点的一环邻域,定义平滑允许区域。如果需要一条最直的测地线曲线,即上述的t=0的情况,则应允许曲线在整个网格上自由移动。
1.4 曲线平滑迭代
网格模型表面曲线生成算法的核心是初始化后的迭代平滑阶段。在此过程中,曲线上的点可以沿着网格模型的边自由移动,但需要保证每个曲线点都始终在某个面片的边上,并且每个顶点的平滑过程中不会移动到边的两端点上。该方法在对曲线点pi进行平滑时存在两种情况:pi在边上或者在顶点上。在第一种情况下,pi可以向两个方向移动,移动终点在该边的两顶点,或者在跨越边缘的一个顶点上。第二种情况需要分割:当点离开顶点时,需要新的曲线段,如图2所示。因此,pi必须被分割成多个曲线点,每个点都位于与顶点相关联的边上。迭代中的一个曲线平滑步骤包括所有曲线点的松弛。在对pi点进行平滑时,对pi的所在面片域进行提取,如图3所示,并将该区域以线段pi-1pi和pipi+1分成两部分,将这两部分分别展开,在两个区域内移动pi点,使得折线pi-1pipi+1最短,取最短长度的点作为调整后的pi点。如上所述,在pi位于某些特殊顶点处时,平滑过程中可能需要添加新的顶点,这就需要将原曲线分割为多段然后参与下一步迭代。
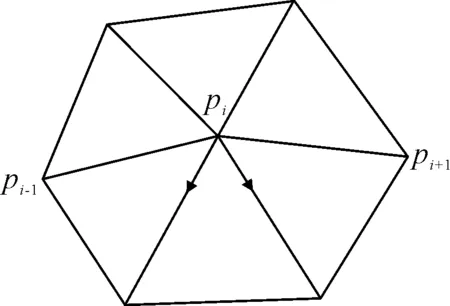
图2 点pi的分散平滑迭代
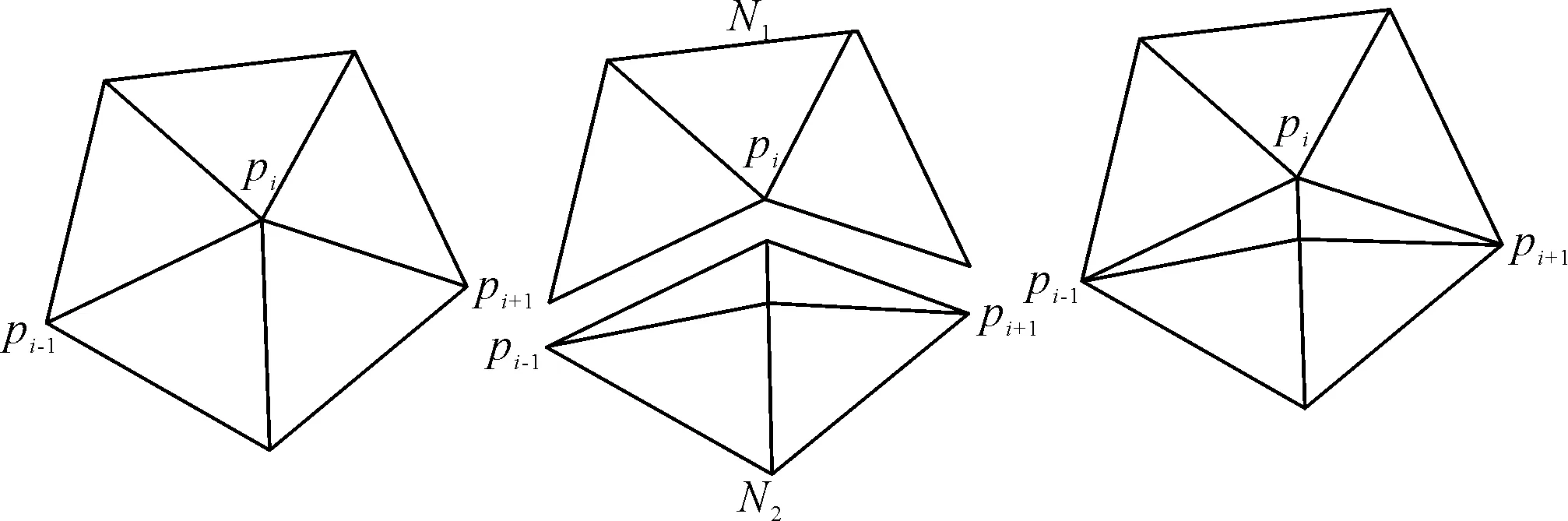
图3 点pi的平滑迭代
1.5 终止条件
在每次迭代之后,都需要对表面曲线上点的位置进行检查,检查其是否出现在合理的位置、曲线的曲率是否满足要求,以此来决定是否进行下一步迭代。因此,引入曲率限制与移动区域限制来实现算法的终止。除了平滑的迭代步数到达上限,额外采用两个评价标准来决定算法的终止。第一,平滑后的曲线不应该离初始曲线太远,因此引入了最大移动距离,将曲线点的移动限制在允许的区域内,这种距离限制可以作为第一种约束,当一个点超出这个区域时,迭代就停止了。第二,定义一个新的百分数τ来表示当前曲率与期望曲率的关系,如果每个当前测地曲率与理想的测地曲率相差的程度小于百分数τ时,就停止迭代。
2 算法流程
首先对算法进行初始化,然后计算预期曲率和计算允许区域来创建输入曲线,并计算所需的测地线曲率和最大基于距离的可行域,然后开始平滑迭代。在每次迭代中,对每个点pi应用以下操作:先计算点的邻域集合N1和N2(图3),然后根据展开的表面选择适当的集合。最后对pi的新位置求值,并且对特殊位置的顶点进行特殊处理,在每一次迭代后都需要判断算法是否满足终止条件。其算法流程如图4所示。
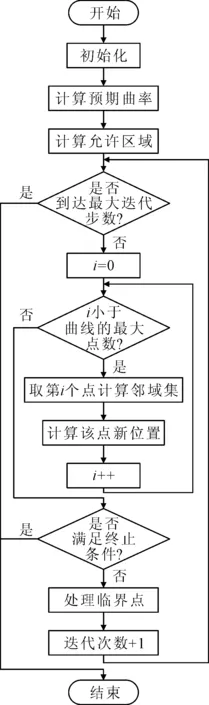
图4 算法流程图
3 应用与讨论
基于Windows平台、Visual Studio开发环境、QT和VTK开源工具,开发网格模型的表面曲线生成系统。系统要求CPU主频在2 GHz以上,内存2 G以上,显存1 G以上。所测试的网格模型是标准椭球模型以及医用外固定支具的关节扫描踝关节模型,该模型通过三维扫描仪获取原始网格数据,并对其进行光顺、简化和切割等预处理操作以保证网格质量。为了便于保存数据提高测试效率,将扫描到的网格模型数据存储为STL格式文件[12-13]。读取STL文件,得到网格模型的点和单元信息,将其转化为特定的数据结构后,使用VTK的内部渲染管线来实现模型的加载和渲染。
将本文算法应用到医用外固定支具网格模型上,如图5所示,分别为椭球模型和踝关节模型,顶点数为1 986和3 968,面片数为30 240和60 111,在定义初始曲线之后执行本算法,分别比较初始曲线和处理后的曲线,并使用网格切割算法进行切割测试。

图5 网格模型
图6和图7为椭球和踝关节网格模型的测试实例。图6(a)中,曲线l1为初始定义曲线,曲线l2为平滑后曲线。并使用网格切割算法进行分割编辑,得到局部分割后的网格模型,如图6(b)所示。由于椭球模型数据量较小,平滑算法对尖锐部分平滑较好,可以实现个性化的设计意图。图7(a)中,曲线l1为初始定义曲线,曲线l2为平滑后曲线。踝关节网格模型含6万余个单元面片,因此初始曲线没有出现明显的尖锐效果,同时,平滑效果较好,使光顺曲线与原始曲线保持接近,并使用网格分割算法完成模型的分割编辑,如图7(b)所示。

图6 椭球网格模型表面曲线
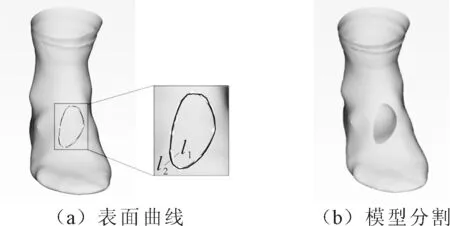
图7 踝关节网格模型表面曲线
本算法的计算消耗主要集中在平滑迭代过程,由于定义高效的数据结构,可快速根据网格拓扑访问邻接点和邻接面片,使顶点位置的搜索变得高效快捷。此外,网格模型的处理效率与其数据量关系密切,顶点数和面片数的增加会导致算法运行时间的几何级数式增长,因此需要控制网格模型的数据量。在外固定支具中,常见的网格模型的数据量在1~3万个顶点左右,本算法运行稳定,可得到光顺的表面曲线。对百万级数据量的网格模型缺乏实验验证,需要进一步研究。
4 结论
笔者以网格模型为对象,提出一种基于测地曲率的网格表面曲线生成方法,采用交互式的方法简化了操作,使用基于测地曲率的表面曲线平滑算法对原始曲线进行迭代平滑处理,引入曲率限制和最大移动距离限制,使最终曲线与初始曲线保持良好的接近度,避免由于过度平滑导致的曲线特征消失。同时,本算法结合医用外固定支具扫描网格模型进行实验验证,得到了较好的表面曲线平滑结果,降低网格编辑操作的难度,为操作人员提供便利的交互。
