平行式电驱桥的传动效率理论建模研究
2021-09-27潘运平吴昌权廖烈平
潘运平,周 恩,吴昌权,廖烈平
(1.武汉理工大学 机电工程学院,湖北 武汉430070;2.湖北车桥有限公司,湖北 荆州 434300)
目前市场上的新能源汽车主要是纯电动汽车和混合动力汽车[1],其中纯电动汽车是新能源汽车的最终目标。传动系统是纯电动车的核心系统,其效率直接影响整车的续航里程和功率密度。因此在传统燃油车的基础上,去掉离合器、变速箱和传动轴等部件,将电机集成到驱动桥上[2],这样可以有效收缩传动链的长度;同时电机相比内燃机有更大的转速范围,可以直接对电机进行控制来实现变速。这样使得传动系统都集成在电驱桥上,因此对电驱桥的效率研究非常重要。平行式电驱桥对整车的动力性、舒适性和燃油经济性都有较大影响,在获得电驱桥系统内部功率损耗的影响因素后,可以在此基础上提高传动系统的效率,减少能量损失,且为新型电驱桥的研发与设计提供理论支撑。
以某4.5 t纯电动物流车的平行式电驱桥传动系统为研究对象,分析从主减速器到半轴传动过程中的功率损失,建立总功率损失的理论模型,并且与试验结果进行对比。
1 平行式电驱桥传动系统结构
平行式电驱桥总成结构如图1所示,电机采用平行式布置,且集成到驱动桥上。传统燃油车驱动桥主减速器采用准双曲面齿轮副进行减速增扭,而平行式电驱桥由于集成了电机,因此采用两级斜齿圆柱齿轮副进行减速。其传动系统结构简图如图2所示,传动系统部分实物如图3所示。
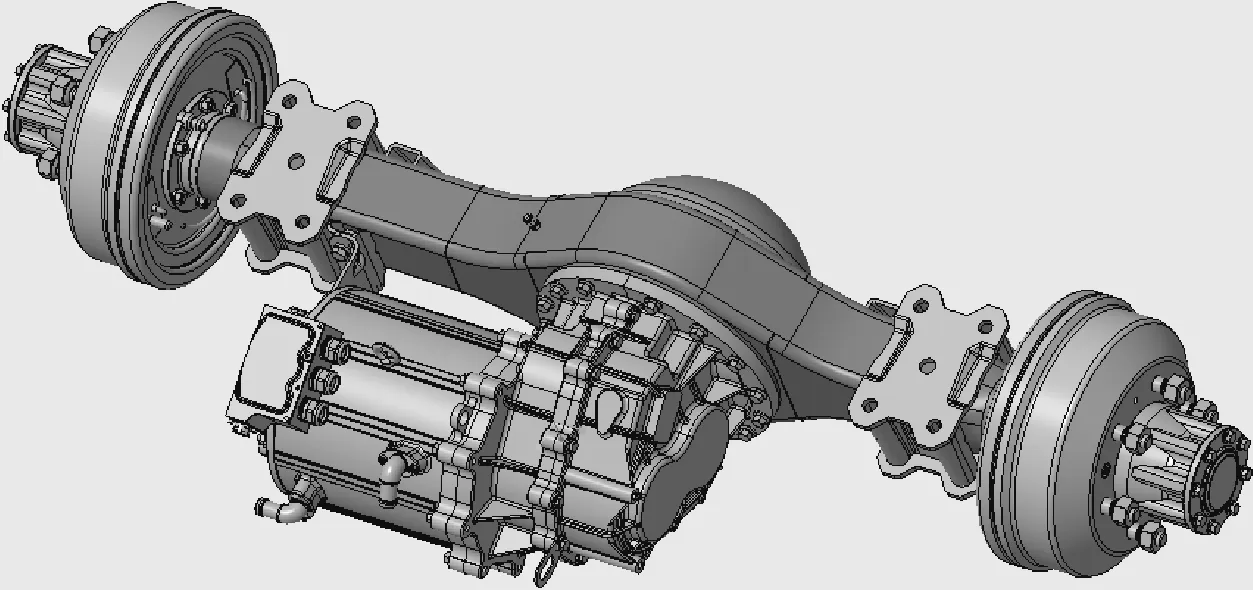
图1 平行式电驱桥总成结构

图2 传动系统简图

图3 传动系统实物图
汽车在行驶过程中,传动效率由传动系统各个部件的功率损失决定。在输入功率一定时,内部消耗的功率越少,传动效率越高,能量有效利用率越高。整体传动系统的功率损失包括齿轮啮合过程中轮齿之间相互摩擦造成的功率损失、滚动轴承摩擦功率损失以及旋转件(主要是齿轮)与润滑油和空气之间摩擦造成的功率损失。
2 齿轮啮合功率损失
齿轮传动过程中的一部分功率损失是齿轮啮合功率损失,齿轮啮合功率损失包括滑动摩擦功率损失和滚动摩擦功率损失。
2.1 斜齿轮平均滑动摩擦功率损失
图4为齿轮啮合时,从动齿轮在C处(此时实际啮合点C在节点K之前)的受力简图,其中N1N2为理论啮合线,AB为实际啮合线[3],T1、T2分别为输入、输出扭矩,α为分度圆压力角,Fn2为从动轮所受的法向力,f为滑动摩擦系数,i为传动化,w1、w2分别为主、从动轮的角速度。齿轮瞬时滑动摩擦损失功率为:
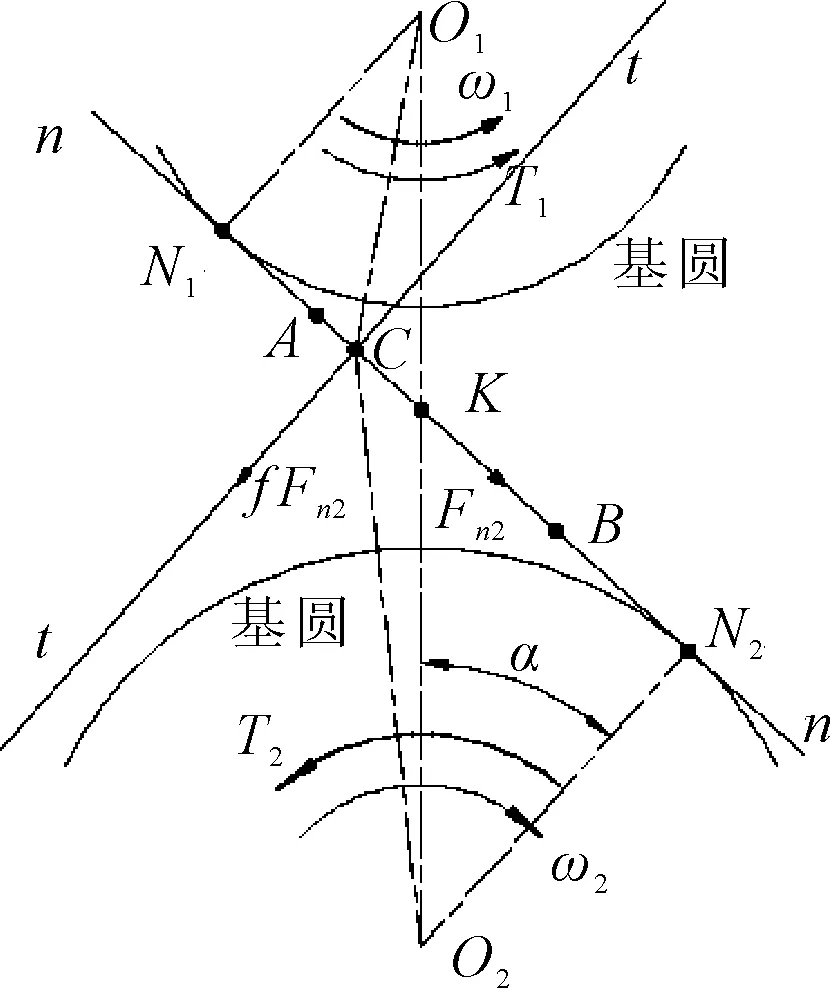
图4 从动齿轮受力简图(C在K之前)
Ps=P1ls
(1)
式中:P1为主动齿轮的输入功率;ls为瞬时滑动摩擦功率损失比[4]。ls计算公式为:
(2)
式中,P2为从动齿轮的输出功率(此处不考虑滚动摩擦)。
结合图4以及功率的计算公式可以得出:
P1=T1ω1=(Fn2|O1N1|-fFn2|N1C|)ω1
(3)
P2=T2ω2=(Fn2|O2N2|-fFn2|N2C|)ω2
(4)
式中:Fn2为从动轮的法向力;O1N1、O2N2分别为主动轮和从动轮轮心到理论啮合点N1、N2的距离;N1C、N2C分别为理论啮合点到实际啮合点C的距离。
结合传动比的定义、式(3)和(4)以及图4上面的几何关系可以对式(2)进行进一步的计算,并且对C在K之后的情况也作同样的计算,可以得到:
由式(2)和式(5)可知,滑动摩擦功率损失与输入功率、传动比、分度圆压力角、齿轮滑动摩擦系数以及实际啮合点位置有关。齿轮副的滑动摩擦系数与齿面间的润滑状态有关。齿面之间的润滑状态通常分为3类[5]:弹性流体动力润滑状态、边界润滑状态和混合润滑状态。这里的齿轮传动属于混合润滑状态,滑动摩擦系数f取平均值0.05。
进一步整理式(5),得到式(6),然后对x求导,在分析ls以及ls关于x的导数后,将第一对斜齿轮的相关参数代入(i=3.5),得出ls关于x的图像,如图5所示。根据式(6)可以知道ls在x=1前后均是关于x的类反比例函数,但是由于这里的值域范围太小,因此图5中的图像看起来是两条直线,实际上是两条类反比例函数图像。

图5 ls关于x的图像
(6)
单对齿轮平均滑动摩擦损失功率为:
(7)
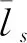
(8)
式中:x1为N1A和N1K长度的比值(也就是实际啮合点在极限点A时),x2为N1B和N1K长度的比值(也就是实际啮合点在极限点B时)。
2.2 斜齿轮滚动摩擦功率损失
闭式齿轮在传动时,润滑状态为混合润滑状态。此时,两齿面之间既有弹性流体动力润滑,又有干摩擦以及边界润滑。在齿面干摩擦区域,轮齿之间为固体接触,将齿面视作刚体,也就是这种区域只存在相对滑动速度,不存在相对滚动速度,即该润滑状态没有滚动摩擦功率损失。在弹性流体动力润滑以及边界润滑区域,由于齿廓之间弹性动力油膜的压力分布不均匀,导致油膜发生变形,从而产生相对滚动速度,由此产生滚动摩擦功率损失。圆柱齿轮滚动摩擦损失功率的经验公式[6]为:
(9)
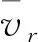
弹性动力油膜的厚度经验公式[7]为:
(10)
式中:ζ为润滑油的压粘系数,平行式电驱桥采用的牌号为GL-4 75W-90的多级齿轮油润滑,GL-4是美国API标准,对应的中国标准为中负荷车辆齿轮油CLD,基础油为精炼矿物油,加添加剂。一般矿物油的压粘系数为1~3×10-8m2/N;μ为润滑油常压下的动力粘度,取0.012 969 N·s/m2;ψ为接触线单位长度所承受的径向载荷的平均值;Ee为等效弹性模量;Rρ为斜齿轮齿廓的综合曲率半径,其计算公式如下:
(11)
式中:r1、r2分别为主、从动斜齿轮的分度圆半径;|AB|为实际啮合线的长度。
3 滚动轴承摩擦功率损失
在轴承工作过程中,其损失功率由摩擦力矩引起。轴承的摩擦力矩计算公式采用Harris提出的模型,将轴承工作过程中的总摩擦力矩分为由载荷引起的摩擦力矩和非载荷引起的摩擦力矩两部分[8]。
在计算滚动轴承摩擦功率损失时,首先需要对3根传动轴进行受力分析,得到6个轴承分别承受的轴向力和径向力,然后求出每个轴承的当量动载荷[9],进而求出轴承的摩擦力矩,最后得到每个轴承的摩擦损失功率。
轴承摩擦损失的功率可以表示为[10]:
(12)
式中:Pb为轴承摩擦损失的功率;M0为非载荷引起的摩擦力矩;M1为由载荷引起的摩擦力矩;nb为轴承转速。
M0与润滑油的运动学粘度、轴承类型以及轴承转速有关,其经验公式为:
(13)
式中:f0为综合润滑和轴承类型的系数;ν为润滑油的运动粘度,所采用的润滑油的运动粘度为14.41 mm2/s;dm为轴承节圆直径。
M1与轴承的当量动载荷有关,其经验公式为:
M1=f1Pdm/1 000
(14)
式中:f1是一个与轴承结构和载荷有关的系数;P为轴承的当量动载荷。
4 齿轮搅油以及风阻功率损失
4.1 齿轮搅油功率损失
搅油功率损失是由于齿轮或者其他旋转件的全部或者一部分浸没在润滑油里面,旋转搅动润滑油造成的功率损失。搅油功率损失属于无负荷功率损失。对于平行式电驱桥而言,搅油功率损失主要是斜齿轮造成的,由于空间布置和体积影响因素的影响,使得只有两个从动齿轮浸入在润滑油中,因此两个主动齿轮不存在搅油功率损失。对于齿轮搅油功率的计算,英国标准ISO/TR14179-1中给出了比较统一的计算公式,以一级从动斜齿轮为例,将齿轮搅油功率损失分为3部分,具体公式[11]如下:
与光滑轴外径有关的功率损失,如轴类部分,其功率损失为:
(15)
与光滑盘外径有关的功率损失,如齿轮侧面,其功率损失为:
(16)
与圆柱面有关的功率损失,如齿轮顶面,其功率损失为:
(17)
式(15)~式(17)中:fg为齿轮浸入润滑油的浸入系数,没有浸入取0,全部浸入取1,部分浸入时按照液面高度插值;n2为一级从动齿轮转速;da为齿轮的齿顶圆直径;L为齿轮的长度;Ag为配置系数,取0.2;Rf为齿轮齿面粗糙度系数。
一级从动齿轮总搅油损失功率为:
Pc=Pc1+Pc2+Pc3
(18)
同理,二级从动齿轮总搅油损失功率也做类似计算。
4.2 风阻功率损失
风阻功率损失与搅油损失功率类似,主要是由于齿轮在转动过程中与空气或者油气混合物之间摩擦引起的功率损失。由于传动轴以及轴承等旋转件的直径相对于齿轮的直径而言比较小,因此对风阻损失功率的计算主要考虑的旋转件是齿轮。威尔士大学的Lord对不同类型齿轮的风阻功率进行研究,根据试验数据,得到了不同模数下的风阻损失功率的经验公式。
当齿轮模数为1时,计算公式为:
(19)
当齿轮模数为1.25~4时,计算公式为:
(20)
当齿轮模数为5时,计算公式为:
(21)
式(19)~式(21)中:ρ为空气密度;ω为齿轮的角速度;mn为斜齿轮的法向模数;b为齿宽。
5 平行式电驱桥总功率损失理论模型
5.1 总功率损失仿真计算
以传动系统的齿轮啮合、搅油、轴承和风阻功率损失为基础,结合实际电驱桥的主减速器结构,对电驱桥传动系统进行总功率损失仿真计算,传动系统模型如图6所示。B1,B1,…,B6分别为输入轴、中间轴和输出轴轴承。由于两个主动齿轮G1、G3的体积和直径远小于两个从动齿轮G2、G4的体积和直径,因此只考虑G2、G4的风阻功率损失。可得总功率损失的计算流程如图7所示。
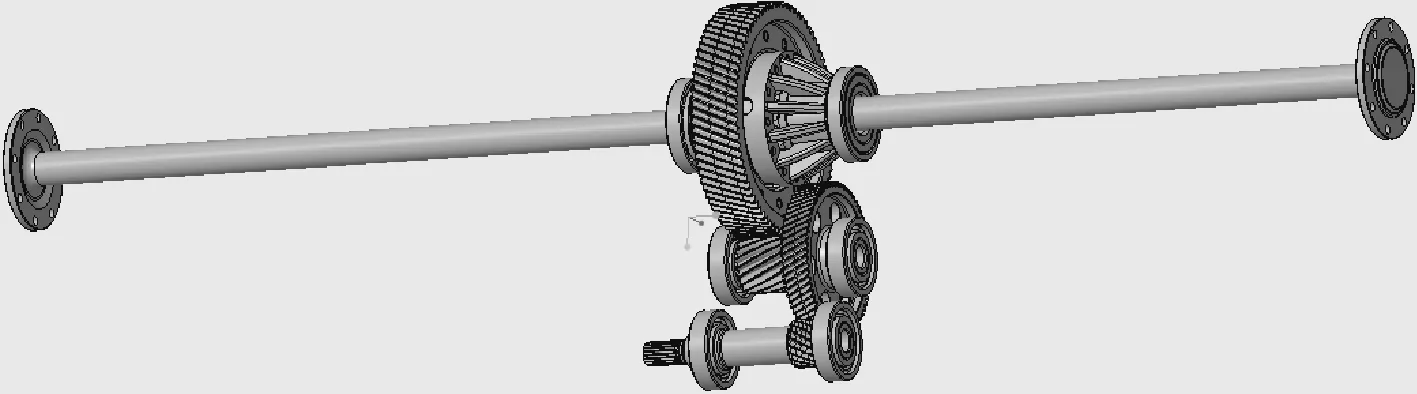
图6 传动系统模型
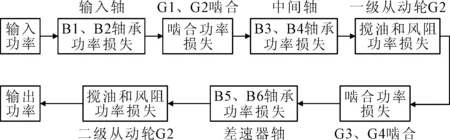
图7 总功率损失流程
根据所建立理论功率损失模型,结合电驱桥传动系统的相关参数,在Matlab软件的Simulink模块中对电驱桥传动系统总功率损失进行了仿真计算,首先在Matlab的命令行窗口输入转速和转矩数组,然后输入代码“t=linspace(0,64,256)’;A=[t,n,T];”,这里是为了定义时间变量,将每个转速以及转矩数据与时刻对应起来,方便后续输入变量文件。搭建如图8所示的仿真模型,将矩阵A的数据导入到Input中,设置仿真停止时间为64.0,示波器里面的采样时间间隔与前面的输入数据进行对应,设置为0.25,最后进行仿真。

图8 电驱桥功率损失仿真模型
仿真结果如图9所示,利用Scope模块对输出数据进行显示。由于电机峰值功率的限制,在其输出转速高于某个值后,其输出转矩的最大值会随着转速的上升而下降,因此图9(b)中转矩峰值在逐步下降。
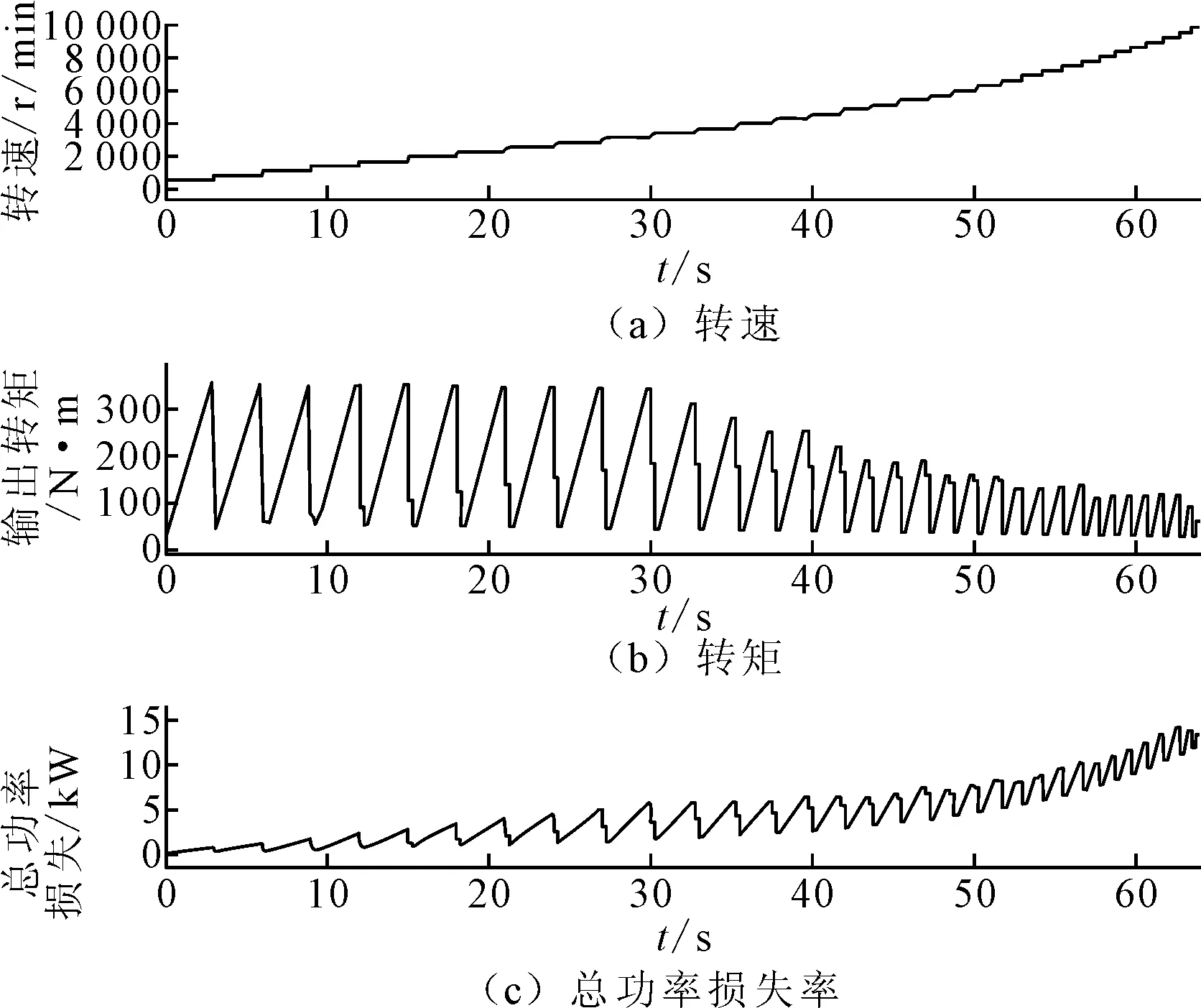
图9 仿真结果
5.2 仿真与试验对比
在得到了总损失功率的计算模型后,还需要与试验结果进行对比。试验值和理论计算值如表1所示,大部分总损失功率的计算值小于对应工况下的试验值,这是因为有部分功率损失没有考虑。功率损失的仿真计算值和对应工况下的试验值之间的最大相对误差为7.06%。由试验数据可知,平行式电驱桥传动系统的最大效率为93.6%,而传统后桥布置方案(与传统燃油车传动系统布置方案一致,只是将内燃机换成电动机)的效率最大为87.48%。平行式电驱桥最大效率相比于传统后桥布置方案提高了7%。
按照试验方案对电驱桥进行试验,其余未进行试验的测试点采用插值得到近似试验值,将试验值和理论值进行对比,得到如图10所示的结果,浅色为总功率损失的试验值,深色为总功率损失的仿真计算值。大部分试验结果都比计算值偏大,但最大误差小于1 kW。由图10和表1的结果可知,总功率损失的理论模型能够对定型电驱桥传动系统效率进行预测,这也为后续传动系统的优化设计(提升效率)提供了理论依据。
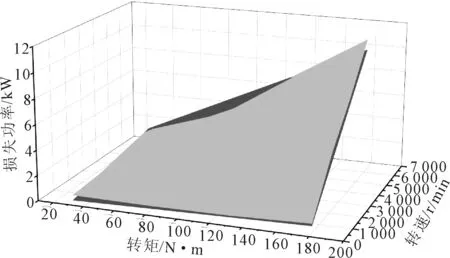
图10 总功率损失理论结果与试验结果对比图
6 结论
(1)以各部分损失功率的理论分析模型为基础,在Matlab中进行了平行式电驱桥传动系统总损失功率的理论计算,并与对应工况下的试验数据进行了对比,二者误差不超过8%,验证了仿真模型的有效性,该理论模型能够为传动部件的优化设计与效率提升提供理论上的支撑。
(2)平行式电驱桥的最大效率值为93.6%,相比于传统后桥布置方案提高了7%,提高了纯电动物流车的续航能力。
