基于零空间追踪的回转窑筒体故障检测研究
2021-09-27余炆哲
余炆哲,张 云
(武汉理工大学 机电工程学院,湖北 武汉 430070)
回转窑主要由筒体、轮带、托轮、大齿圈等组成。窑长期在高温、重载、多尘等恶劣条件下低速不间断运转,因运行和调整不当,窑经常发生故障[1]。据行业统计,回转窑主要故障是筒体弯曲形变和窑中心线发生偏移[2]。如果窑的弯曲和窑中心线偏移严重会对某些托轮造成异常超载,导致托轮轴瓦高温失效发生停产事故[3]。因此通过对托轮位移振动信号进行检测,早期发现故障和主动维护,减少窑停产事故,具有工程实际应用价值。
Zheng、赵晨等首次建立托轮振动模型并研究内在机理,通过测量的托轮位移信号可以判断筒体热弯曲故障与中心点水平偏移故障。他们采用集总经验模态分解(complete ensemble empirical mode decomposition, CEEMD)提取振动信号的特征谐波,取得了一定进展[3-4]。CEEMD本质上是一种噪声辅助算法,对第一类模态混叠有一定抑制作用,但其噪声幅值系数与集总次数设置较为困难。秦岭、卢振东采用双树复小波变换(dual tree complex wavelet transform, DTCWT)和变分模态分解(variational mode decomposition, VMD)对振动信号的特征信号提取取得了一定的效果[5-6]。然而上述信号分解方法存在一些缺点,DTCWT算法由于滤波器负频率通带的重叠所造成的混叠效应,导致滤波器的选择非常困难。VMD算法由于参数的选择差异性非常明显。
针对上述处理方法的不足,考虑工程应用要求简易可靠,笔者提出了一种基于零空间追踪(null space pursuit, NSP)的算法来提取筒体故障的特征信号。
1 托轮受力分析及其与窑故障的关系
在回转窑运转中,窑筒体的重量由托轮承受,回转窑发生故障时,托轮的受力也会发生变化,由于每挡托轮都是对称安装,理论上左右托轮的受力形式相同,将筒体与轮带看做一个整体,其受力关系如图1所示。
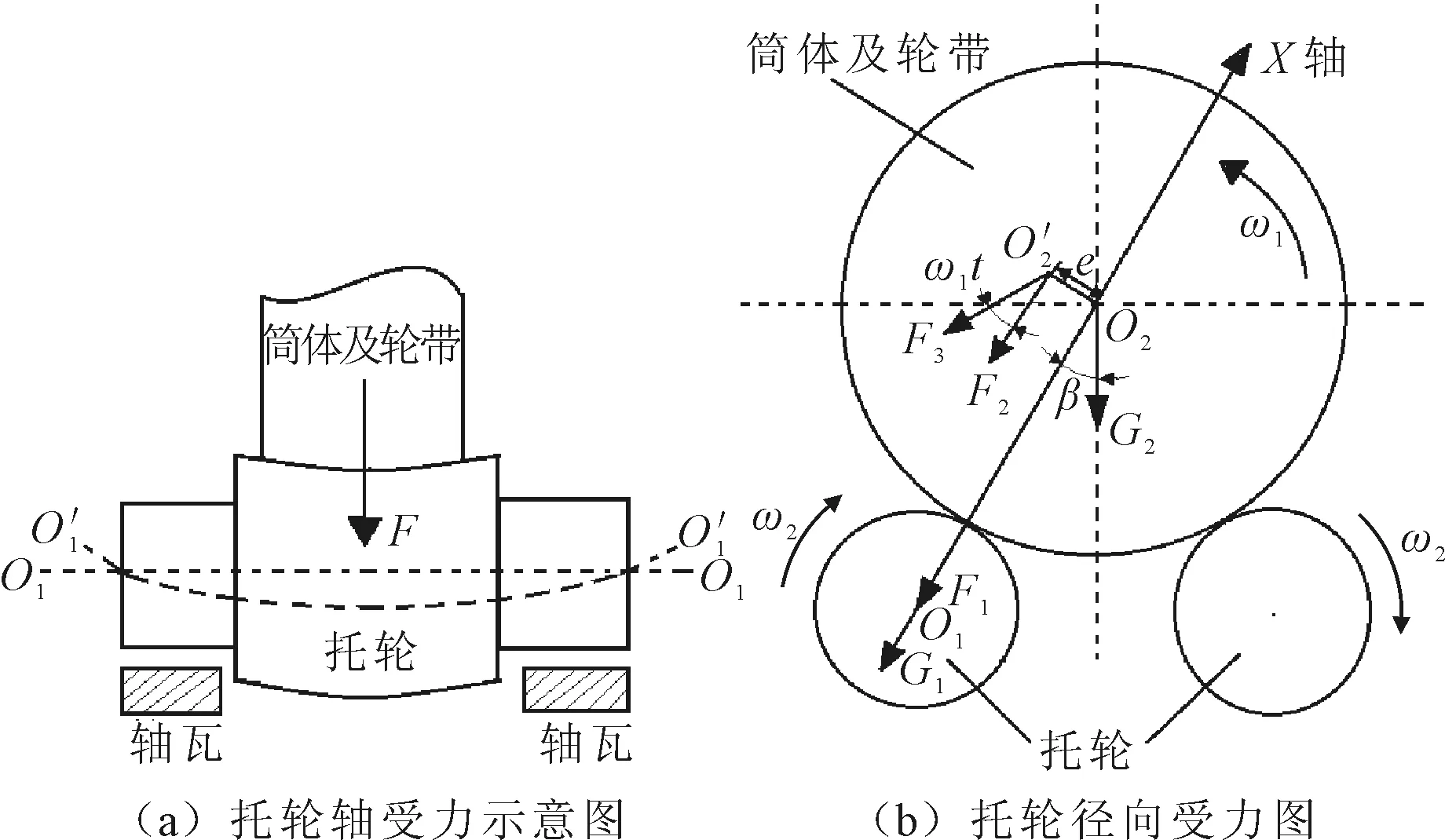
图1 托轮受力示意图
图1中,O1为托轮的旋转中心;O2为筒体的回转中心;O′2为筒体在截面处的几何中心;ω1为筒体的角速度;ω2为托轮的角速度;G1为托轮重力在接触方向上的分量;G2为筒体与轮带的等效重力;F为托轮的弯曲受力;F1为托轮受到筒体与轮带的等效压力;F2为托轮在X方向受到筒体的动载荷;F3为筒体产生的离心力。
取托轮中心与回转窑旋转中心连线为X轴,则在X轴上托轮所受到的力F为:
F=G1+F1+F2
(1)
该托轮受到的筒体压力为筒体重力的分量,m1为筒体与轮带的等效质量,β为筒体中心与托轮中心连线与竖直方向的夹角,一般为30°。则:
F1=m1gcosβ
(2)
如果筒体弯曲的偏心量为e,则筒体产生的离心力为:
(3)
离心力F3在X轴上的分量即为托轮受到冲击产生的动载荷为:
(4)
故F为:
(5)
根据材料力学,可将托轮轴看做简支梁模型,在筒体冲击压力的作用下,根据相关公式可得冲击产生的挠度为:
(6)
式中:a为托轮轴看做梁的等效长度;EI为托轮的刚度。
考虑筒体的压力导致托轮的变形,则由于托轮自身变形产生的挠度为:
s2=ζcos(ω2t+φ)
(7)
其中,ζ为筒体挤压冲击导致托轮和轴瓦之间产生的形变量;φ为托轮旋转的相位角。则托轮轴的挠度为:
s=s1+s2
(8)
计算得:
s=k1cos(ω1t)+ζcos(ω2t+φ)+k2
(9)
由受力分析可知,托轮位移振动信号中包含筒体的频率成分ω1和托轮的频率成分ω2,将其定义为KF(kiln frequency)谐波和RF(roller frequency)谐波。近期的研究成果表明,托轮位移信号的幅值与托轮故障之间存在着紧密联系[3-4],当筒体的弯曲程度增大时,KF谐波的幅值增大;当筒体的中心线偏移程度加深时,大载荷托轮的RF谐波幅值增大。因此可以用比较RF、KF谐波幅值的大小比值来反映回转窑的故障状况。
2 故障特征提取算法研究与适用性验证
由于托轮位移信号属于非平稳信号,其所参杂的噪声信号非常复杂。对于上述非平稳信号特征分量的提取问题,Peng等利用算子零空间的理论,提出了一种基于算子的信号分解方法[7],即零空间追踪算法NSP。
2.1 零空间追踪算法原理
零空间追踪算法是根据信号中的子成分按照窄带信号分量进行提取分解的算法。假设存在如下窄带信号模型:
S(t)=A(t)sin(ωt+φ(t))
(10)
式中:A(t)为信号S(t)的幅值,最大频率小于ω,φ(t)为相位变化函数。
对于S(t),假设T为局部线性算子[8]。对于在任意的时间t上存在,在其一定的邻域内满足条件:
T(S)(t)=0
(11)
那么认为S(t)存在于算子T的零空间之中。
假设一系列算子作用于S(t)上,则该算子零空间信号成分依次被消除,最终剩余分量不包含任何算子相关信息,即:
S(t)=U(t)+V(t)
(12)
式中:U(t)为算子T提取的零空间分量;V(t)为迭代后的S(t)的剩余分量。
采用最优化方法寻找U(t)。这里考虑存在信号S(t)和线性算子T。满足:
T(S)(t)=V(t)
(13)
U(t)是对应算子T的映射空间中的值为零的区间。为获得U(t),定义:
V(t)=min{‖T(S-V)‖2+λ‖D(V)‖2}
(14)
式中:λ为拉格朗日系数;D为正则运算。
U(t)如果由U(t)=S(t)-V(t)直接提取,则很难被准确的提取出来,根据参考文献[9],式(14)改写成:
V(t)=min{‖T(S-V)‖2+
λ1(‖V‖2+γ‖S-V‖2)+F(t)}
(15)
式中:λ1为拉格朗日系数;γ为泄露因子;F(t)为算子T的拉格朗日参数,将局部线性算子T采用二阶微分算子:
(16)
那么式(16)改写成:
λ1(‖V‖2+γ‖S-V‖2)+λ2‖DA(t)‖2}
(17)
式中:λ2为F(t)的拉格朗日系数;D为2阶微分算子。
为将信号分解成多个窄带信号,将式(17)进行多次迭代,算出每次迭代中信号分量V(t)和U(t)。
该算法根据信号的特征设定出特定的局部线性算子,并利用该算子将原始信号分解成局部窄带信号,经过多次分解,可得到若干属于算子零空间的局部窄带信号,将其作为基本信号即可得到原始信号的近似表示,窑振动信号的特征故障频率KF,RF可作为其基本信号的叠加,实现原信号的分解。
2.2 托轮位移信号仿真
回转窑在重载高温和恶劣环境下运转,考虑相关因素对托轮位移信号的影响,构造相应的仿真信号如下:
(18)
式中:x1为模拟与筒体旋转频率一致的特征谐波;x2为模拟与托轮旋转频率一致的特征谐波;x3为模拟托轮由于形变以及受力不均等故障等故障产生的高斯脉冲噪声信号;x4为所有信号的叠加,其时域波形如图2所示。
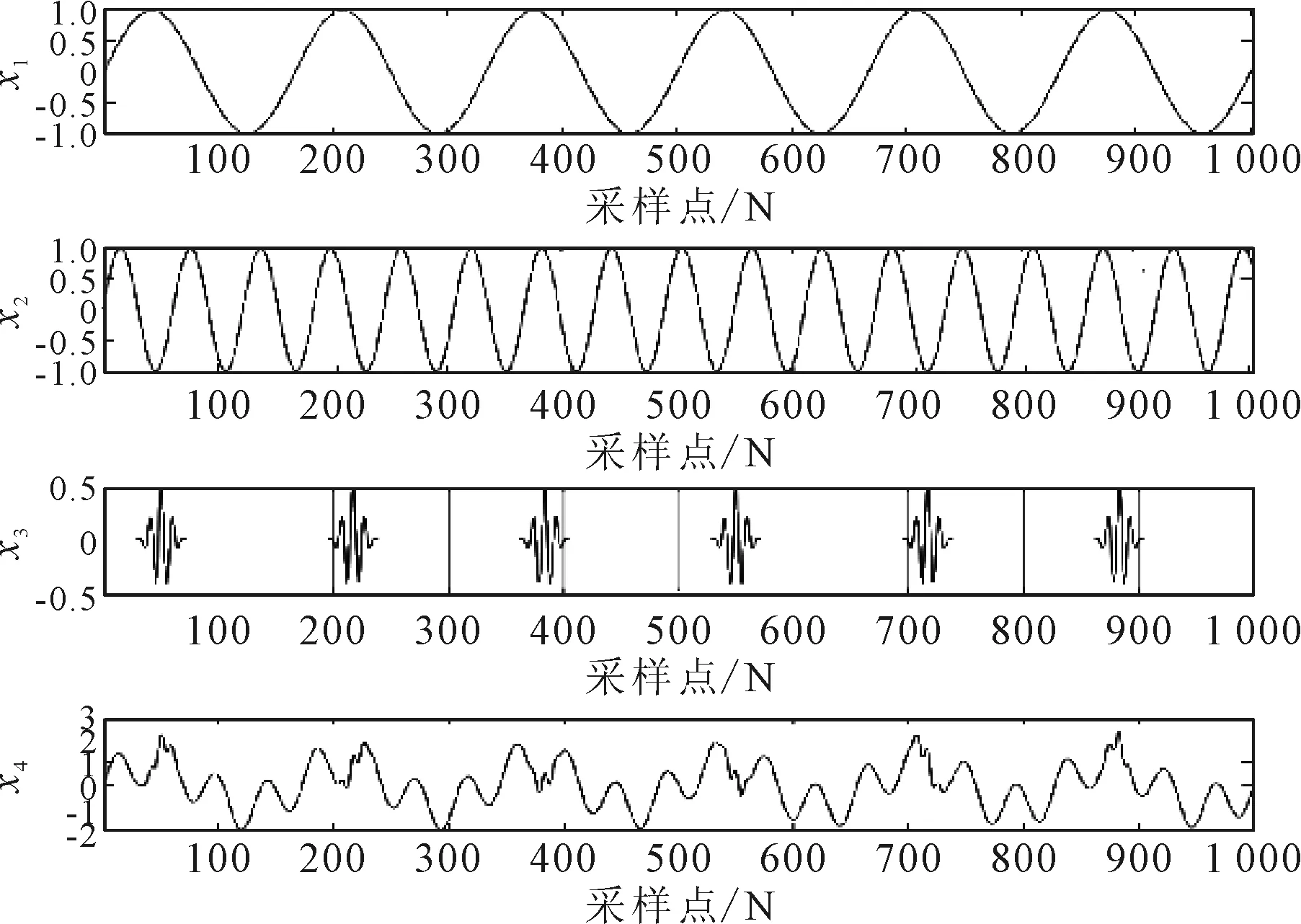
图2 仿真信号时域图

将仿真信号x4进行CEEMD分解,分解层数设置为5层,分解结果如图3(b)所示。把图3(b)与图3(a)对比可看出,CEEMD分解效果较差,其模态混叠情况严重,分解后信号分量与仿真信号x1和x2差异较大。NSP方法比CEEMD方法在特征提取上更具优越性。
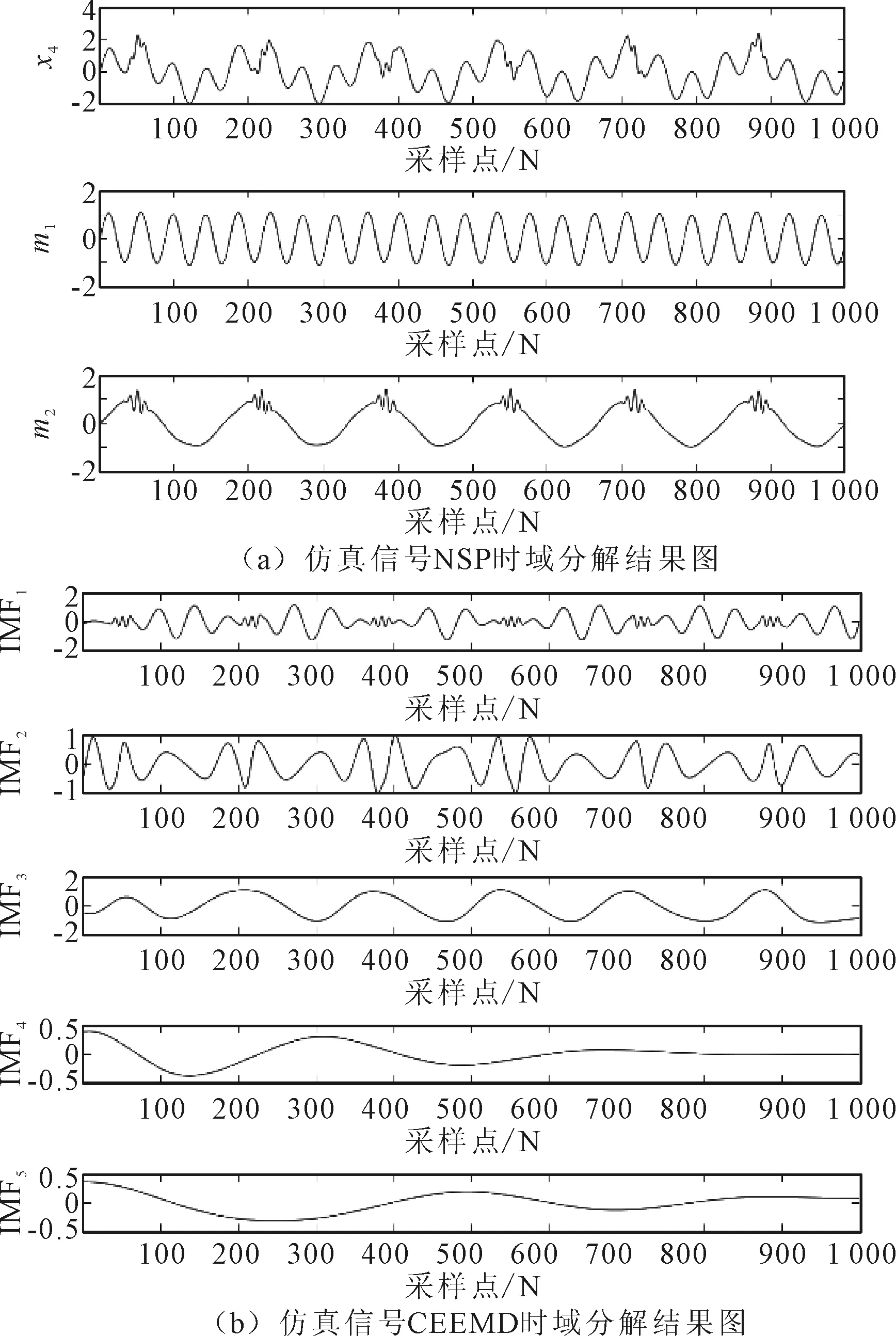
图3 仿真信号时域分解结果
3 实际托轮位移信号的NSP处理验证
3.1 实际托轮位移信号的NSP分解
选取某水泥集团5 000 t/d回转窑托轮位移实际测量数据进行故障诊断的验证。该窑筒体托轮的回转频率如表1所示。

表1 窑筒体与托轮的回转频率
测量仪器设定的采样频率为100 Hz,采样时间为80 s。对托轮位移测量信号进行NSP分解,其结果如图4所示。分解的迭代次数为3次,迭代参数如表2所示。

表2 零空间追踪相关参数表

图4 对托轮位移信号的NSP分解结果
从图4可知,对托轮位移信号进行3层NSP分解,其左侧为分解的IMF时域图,其右侧为IMF的频谱图。由各频谱图看出第一个IMF分量中明显反映出筒体特征频率KF;第二个IMF分量中明显反映出各托轮特征频率RF。
在提取的IMF1和IMF2分量中,均可以用故障特征谐波的平均能量来反映故障程度,计算式如下:
(19)
式中:xi为分解分量中信号的幅值;n为信号的样本容量。
为消除信号长度对结果的影响,提高计算精度取其能量的均值。其结果如表3所示。
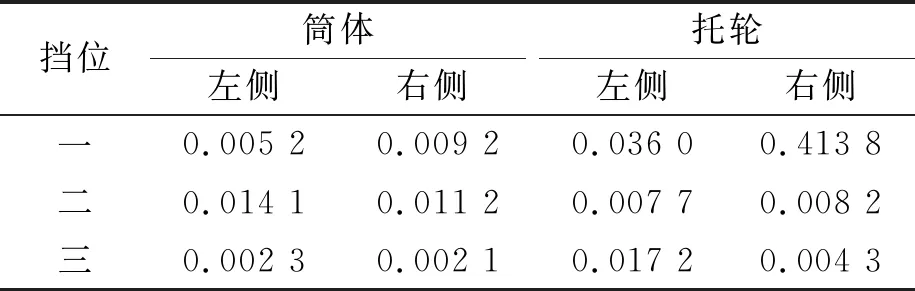
表3 某窑筒体与托轮分量的平均能量 mm2
3.2 窑筒体弯曲故障识别验证
通过窑弯曲激光测量仪[10]对该窑筒体弯曲变形进行检测,该筒体测量截面的偏心量结果如图5所示。由各挡左右托轮位移信号分解提取的筒体特征频率KF平均能量如图6所示。
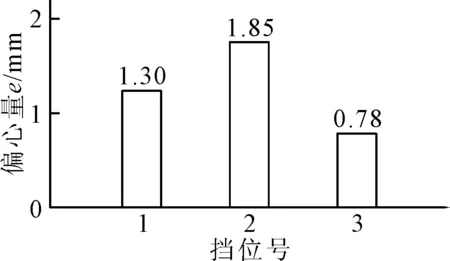
图5 某窑3个挡偏心结果

图6 某窑筒体KF信号平均能量
由图6可知,各挡筒体特征频率KF平均能量值排序为:2挡>1挡>3挡。其结果与图5实际窑弯曲偏心测量结果趋势一致,这些对比验证表明:由托轮位移信号提取的各挡筒体特征频率KF的平均能量值可以快速有效反映窑弯曲变形的故障程度。
3.3 托轮受力不均故障验证
使用筒体椭圆度专利测量仪对窑每挡轮带附近筒体的椭圆度进行测量,仪器随筒体旋转到左右两个托轮时筒体测点的弹性形变量即椭圆度曲线可以线性反映左右托轮受力的大小值。测得结果如图7所示。

图7 窑筒体各截面椭圆测量曲线图
在图7(b)所示的曲线中,椭圆仪随筒体依次经过左托轮、窑最低点、右托轮。根据各条曲线左右峰值大小比例,可计算每个截面的右托轮与左托轮R/L的相对受力比值,其结果如图8所示。
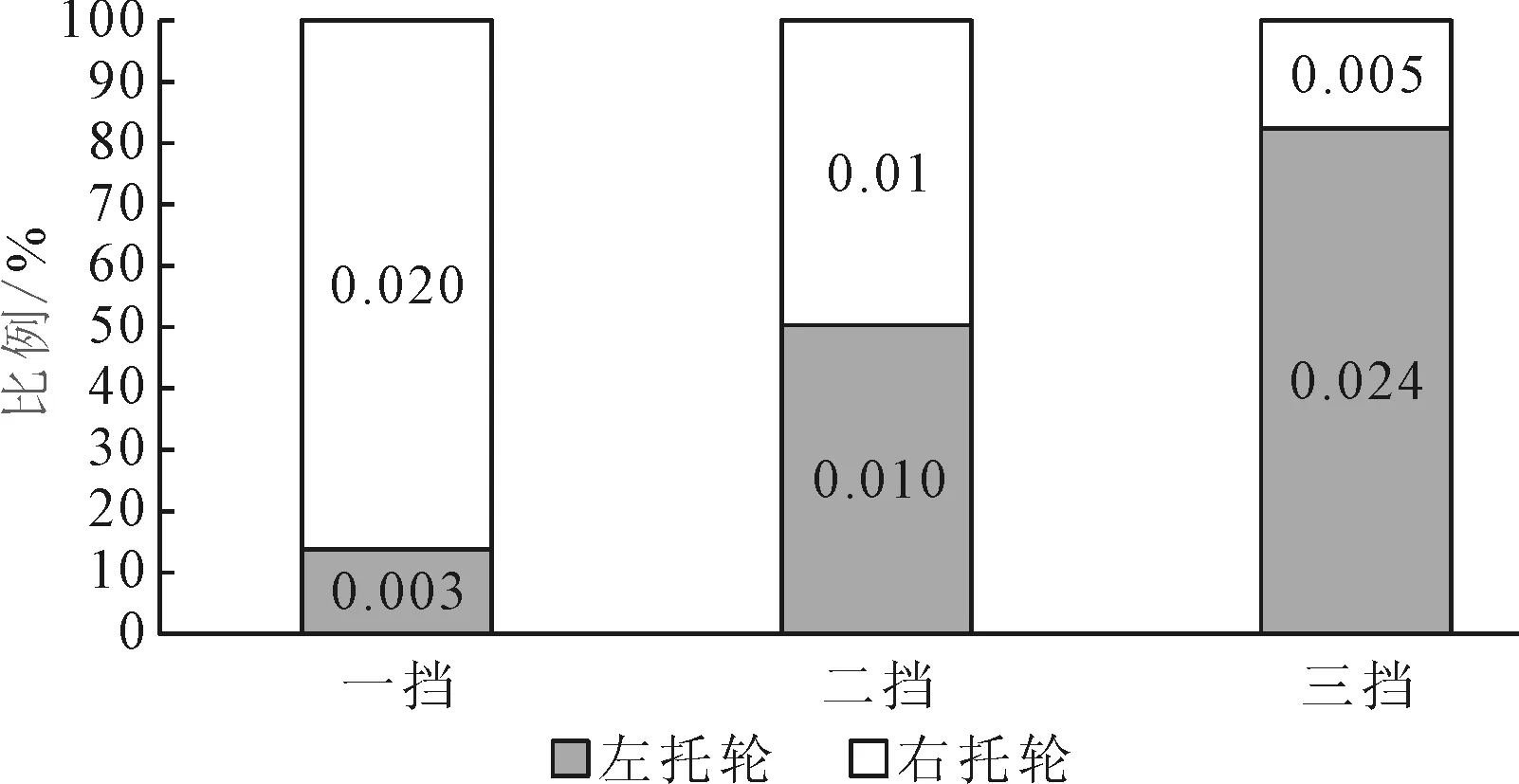
图8 各挡左右托轮受力比例示意图
经过NSP分解提取后,各托轮的特征频率RF的平均能量比例值如图9所示。
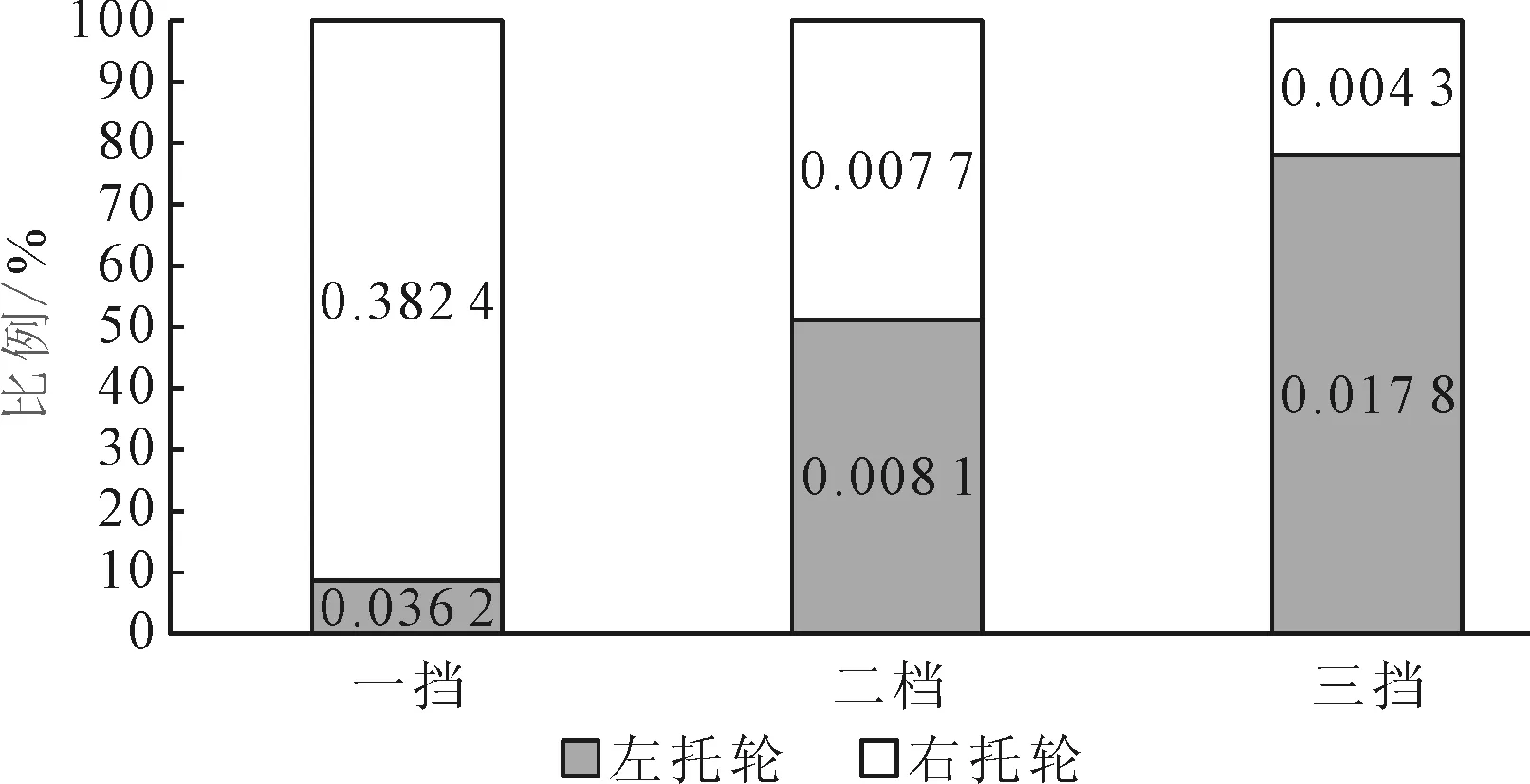
图9 各托轮特征频率RF的平均能量比例示意图
对比图9与图8可知,各托轮特征频率RF的平均能量与椭圆仪测得的各挡左右托轮受力比值结果基本一致。这些对比验证表明:通过托轮特征频率RF平均能量可以简单有效反映各挡左右托轮受力状况。
4 结论
针对目前对回转窑故障特征信号提取方法的不足,笔者提出了一种基于零空间追踪NSP的回转窑故障特征信号的提取方法,该方法运用最优化方程对测量信号进行自适应分解,选取适当的算子在迭代过程中不断更新,使分解与提取窑故障特征频率信号更加准确和高效。该方法对托轮位移实际测量信号的处理结果表明:
(1)使用筒体特征频率KF的平均能量作为评价故障参数,可以有效反映回转窑各挡筒体弯曲故障程度。
(2)使用托轮特征频RF的平均能量作为评价故障参数,可以有效反映回转窑每挡左托轮和右托轮受力状况及超载故障程度。
该方法为检测回转窑的故障识别提出了一种新思路。
