一种分析具有局部非线性动力系统的二次降维方法

杨雄民 陈可轩 闫志勇

(1.杭州汽轮机股份有限公司工业透平研究院；2.浙江省工业汽轮机转子动力学研究重点实验室）

0 引言

对于转子-轴承耦合系统以及其他一些具有非线性结合面的局部非线性动力系统，其系统维数较高,可以达到103以上，虽然非线性自由度只占系统自由度的很少一部分，但却决定着系统的动力特性。直接利用数值方法求解上述系统固有值问题和非线性动力特性，不仅计算量巨大，而且由于舍入误差、求解精度不协调等造成迭代不收敛、轴颈碰擦等迫使计算中断。

围绕系统的降维，众多学者进行了大量的研究，其主要思想是利用模态综合方法降低系统维数，进而通过求解降阶方程来讨论原系统的固有值问题和非线性动力特性。Neleson 等首先引入了模态综合思想，用于复杂转子系统的稳定性分析和瞬态响应分析[1]。Rouch和Kao 利用Guyan 直接缩聚方法来降低转子有限元模型的自由度规模[2]。进一步地，张家忠等提出局部非线性力之作用在系统的个别节点上，把系统的自由度分为线性自由度和非线性自由度，利用模态缩聚方法缩减线性自由度而把非线性自由度完全保留在物理空间中[3,4]。对于局部非线性动力系统，通常关心其静平衡位置的扰动周期解及其分岔，然而上述模态变换方法模态变换矩阵仅仅与结构的质量矩阵、阻尼矩阵和刚度矩阵有关，而没有考虑局部非线性力的影响。由于局部非线性力一般为系统在静平衡位置上扰动位移和扰动速度的函数，与系统的各固有特性矩阵相耦合，共同决定着系统的运动模态形态。郑铁生等首先通过变分原理计算非线性油膜力及其Jacobin 矩阵，在形成系统的阻尼矩阵，刚度矩阵时考虑油膜力的影响，形成系统的模态变换矩阵，进而对原系统进行降阶[5]。考虑局部非线性力的影响，系统质量矩阵一般为对称矩阵，而刚度矩阵和阻尼矩阵为非对称大型带状稀疏矩阵。传统的QR方法势必破坏系统矩阵的上述特点，花费大量的机时和存储空间。Meirovitch方法针对无阻尼回转系统K，M 矩阵对称，D 矩阵反对称情况，无法推广到一般系统[6]。非对称型的Lanczos方法数值稳定性差，而对称性广义Lanczos 方法势必引入大量的复数运算[7]。郑铁生等提出了一种非对称矩阵结构系统固有值分析的广义逆迭代方法，不需要把系统改写为一个2n阶线性问题，直接在原n阶规模上进行反迭代，从而把高维系统固有值问题降阶为一个小型线性标准特征值问题[8]。郑兆昌等把阻尼陀螺系统运动方程转化为一阶状态方程，利用Arnoldi方法对系统进行降阶，进而通过Schur分解把系数矩阵转化为上三角矩阵来求解系统的特征值及动力响应[9]。王陶提出了针对局部非线性问题的混合坐标自由界面子结构模态综合方法[10]。

由于截断误差以及降阶模型阶数选择不合理等因素，使得降阶后系统特征值出现伪根，在利用数值方法计算降维后，系统方程长期动力特性时发散。本文基于广义反迭代思想，提出一种可以用于求解局部非对称非线性系统动力特性的二次降维方法。通过二次降维，把原高维局部非线性动力系统降阶为一个等价的低维系统。针对降维系统周期解的求解，给出其配套打靶法算法。最后以滑动轴承-转子动力系统为例，运用本文算法求解其非线性动力响应。

2 局部非线性动力系统的二次降维

不失一般性，令局部非线性动力系统方程为

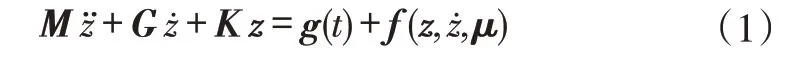
其中，M为系统的质量矩阵，G为系统的阻尼矩阵(陀螺矩阵)，K为系统的刚度矩阵，g(t)为线性激励力，f为系统的非线性力项，只作用在系统的某些局部自由度上，可以表示为

考虑到系统的静平衡方程

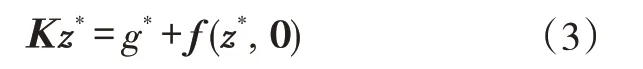
其中，g*为静态线性力，系统运动方程可以简化为

取变换矩阵P和Q满足代入方程（5），可以得到，

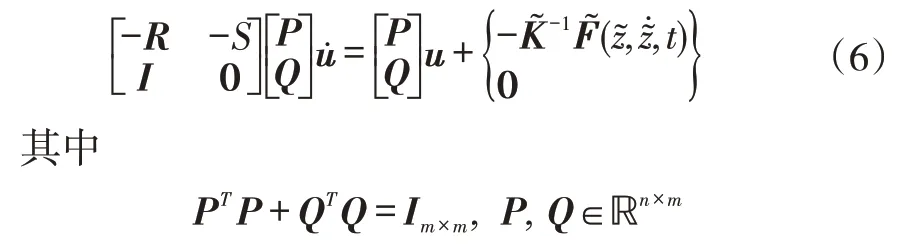
存在上Hessenberg矩阵H∈ℝm×m满足[8]

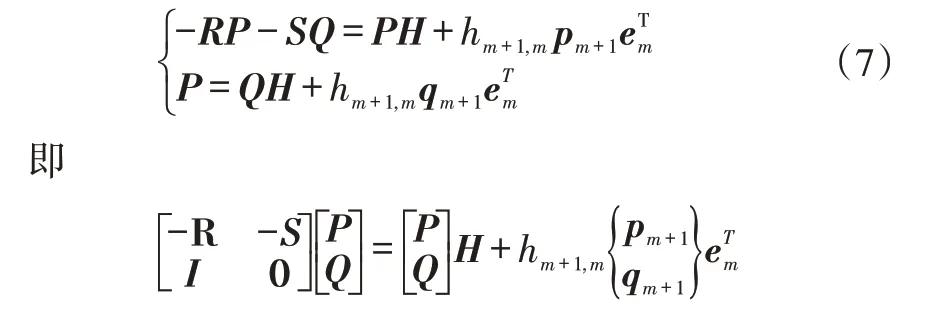
结合方程(6)和方程(7)可得

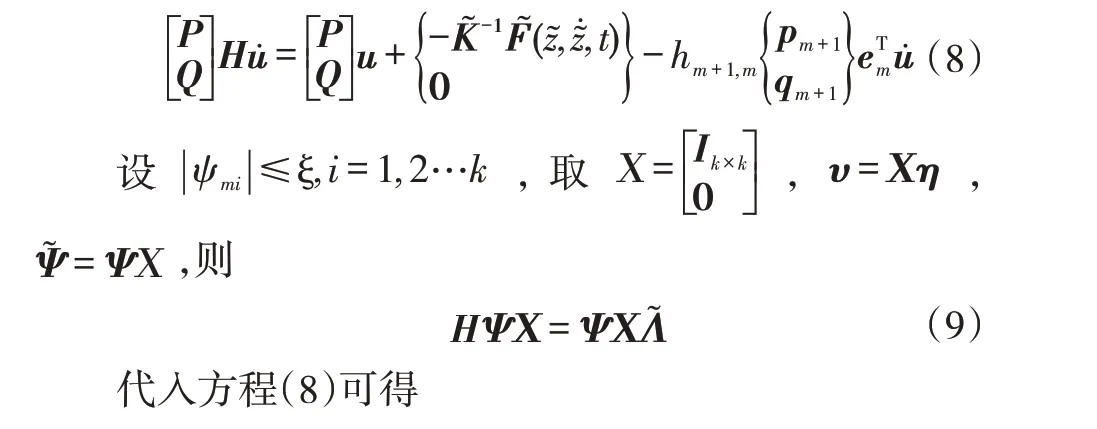
根据方程(11)可以发现，二次降维后系统自由度的维数为k，远小于原系统(1)的自由度n，可以利用直接数值方法如Runge-Kutta法等来研究降维后系统的动力特性。

3 非线性动力特性求解及算法

研究系统平衡位置的周期解及其稳定性具有重要的工程和理论意义。直接采用基于Poincaré点映射的数值积分方法，由于求解局部非线性力及其Jacobin 矩阵如转子-轴承系统需要求解Reynolds 方程，往往要花费大量的机时。构建合适的算法来求解降维系统的周期解，则成为本文算法能否用于工程实际的关键点。二次降维系统非线性动力方程简记为

一般满足非自治系统G(η,t)=G(η,t+T0)。在不引起混淆的前提下定义P为Poincaré 映射，设ηj为系统周期l解在Poincaré 截面上的不动点，则满足

利用Newton-Raphson方法构造如下的迭代格式

对于迭代格式(12)中DηP(ηj)的计算，根据Poincaré映射定义可以按照式（15）进行计算

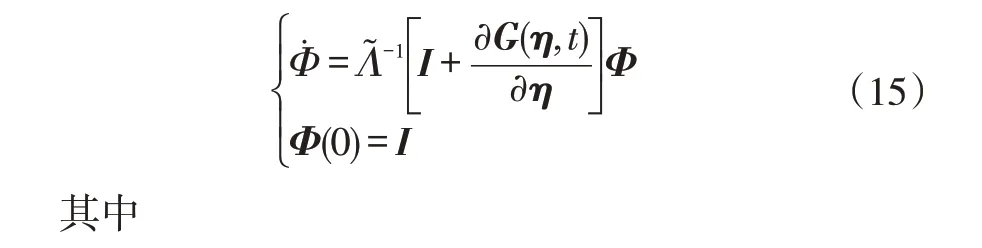
在t=T0时，Φ(T0)=DηP(ηj)即为Poincaré 映射在ηj处的Jacobin矩阵，可以根据Φ(T0)来判断周期解的稳定性。二次降维系统方程（11）和方程（15）同时迭代计算，进而可以根据式（14）打靶得到系统的周期解。

4 数值算例

转子-轴承系统为一典型的局部非线性动力系统。为了验证本文算法，对某一工程实际转子进行非线性动力特性分析。图1某工程轴承-转子系统动力学模型，转子各段长度及其外径如表1 所示，由两个相同的椭圆瓦轴承支承（B1 和B2，轴颈直径140mm，瓦块包角为150°，长径比为1.0，间隙比为0.0025，瓦块预负载系数为0.3，润滑油粘度为0.022N·Sec/m2），附加叶轮（D1-D5）质量及转动惯量如表2 所示。不平衡量施加在圆盘D2 和D4 处，相位分别为0°和180°，大小为3000g·mm。

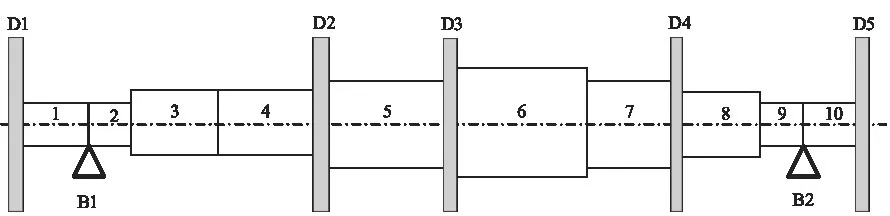
图1 某工程轴承-转子系统动力学模型Fig.1 Dynamic model of rotor-bearing system

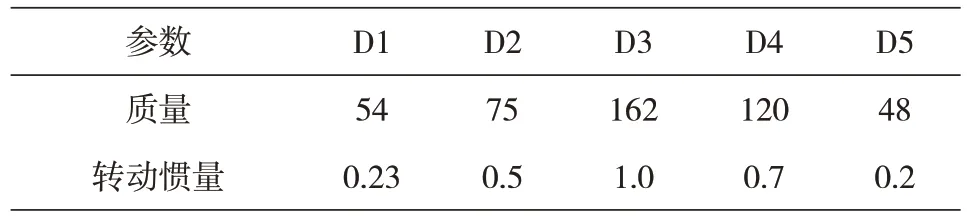
表1 叶轮质量及转动惯量Tab.1 Impeller mass and moment

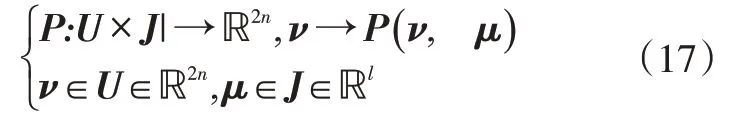
取转速ω=3919rpm 和零初始条件计算其周期解残差，表2 给出了部分降阶模型误差结果对比，可以发现本文算法通过二次降维，避免了因降维阶数m设置不合理而出现伪根，具有较高的计算精度。表3 为ω=3000rpm时利用打靶法求解系统周期解的迭代过程，其中第一次打靶初始条件为η=00，可以发现本文周期解打靶收敛速度极快。

表2 不同降阶模型计算响应的误差Tab.2 Calculated response errors of different reduced order model

表3 打靶法求解周期解误差Tab.3 Periodic relative errors calculated of shooting method

图2为以转速为参数系统分岔图，其中横轴转速从2000rpm 到20000rpm，纵轴为B1 点x方向位移。从图2可以看出，转速小于3919rpm时，为周期1解；到转速大于3919rpm 时，Floquent 乘子在-1处通过复平面上的单位圆，周期1 解失稳而发生倍周期分岔，分岔后系统由不稳定的周期解变为稳定的倍周期解。当转速增至4400rpm 时，倍周期解的一对共轭Floquent 乘子通过复平面上的单位圆，发生准周期分岔。随着转速的增加，系统基本呈现为准周期解。从图2可以看出，在某些转速下仍有一些周期窗口出现，即出现各种亚谐振动（模态锁定现象）。图3为转速6869rpm时系统B1点的轴心轨迹和Poincaré 图。由图3 可以看出，Poincaré 截面上的不动点已突变为环面集，系统为准周期运动。图4为转速18809rpm 系统的1/7 亚谐运动。图6 为转速14000rpm 系统B1 点的轴心轨迹、时间历程曲线、Poincaré 图和功率谱图，可以发现其吸引子已呈现明显的分数维特征，响应曲线包含了丰富的低频特征，系统已进入混沌运动。

图2 B1点分岔图Fig.2 Bifurcation of Point B1

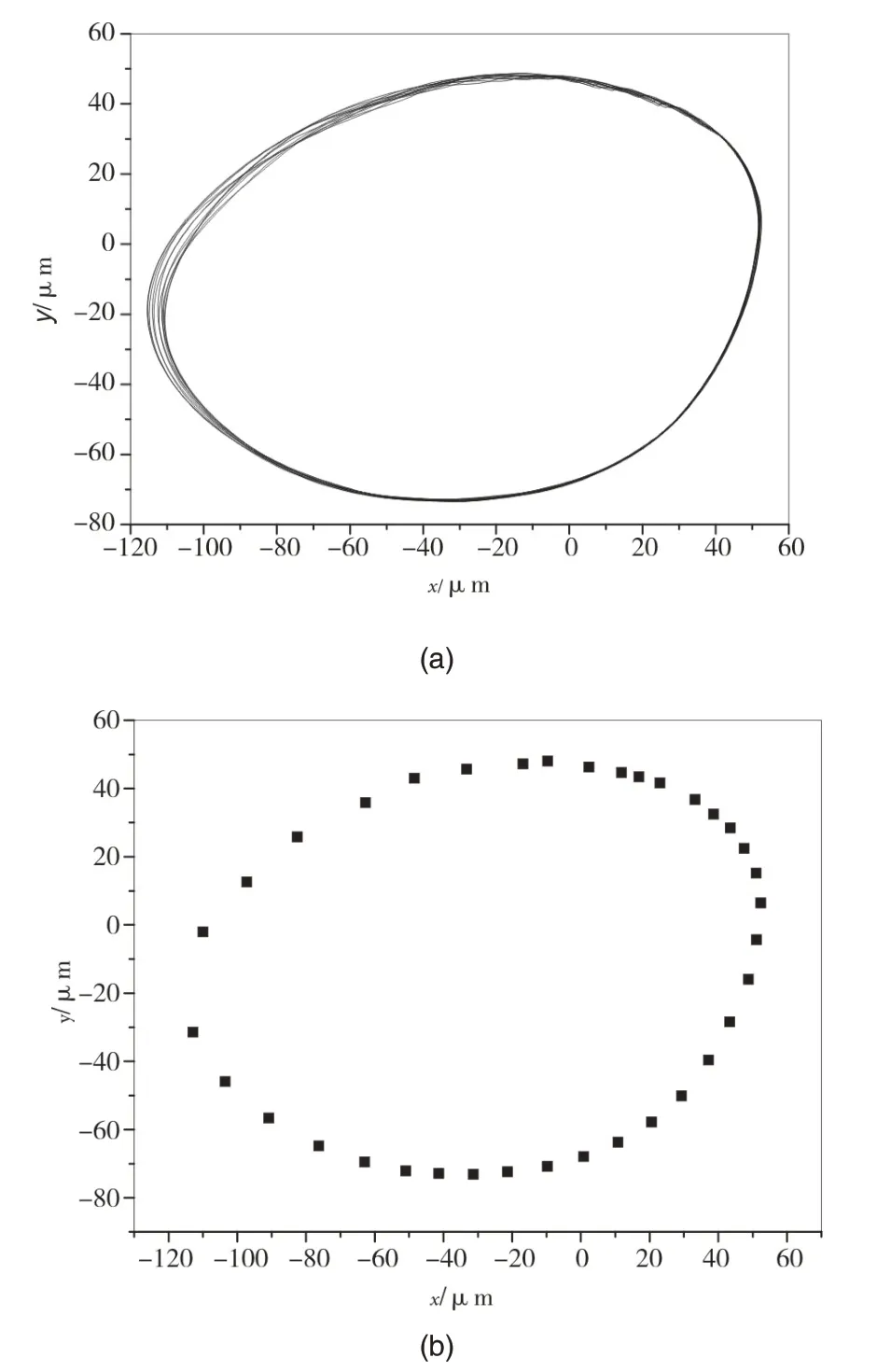
图3 准周期运动Fig.3 Quasi-periodic motion

图4 1/7亚谐运动Fig.4 1/7 sub harmonic motion

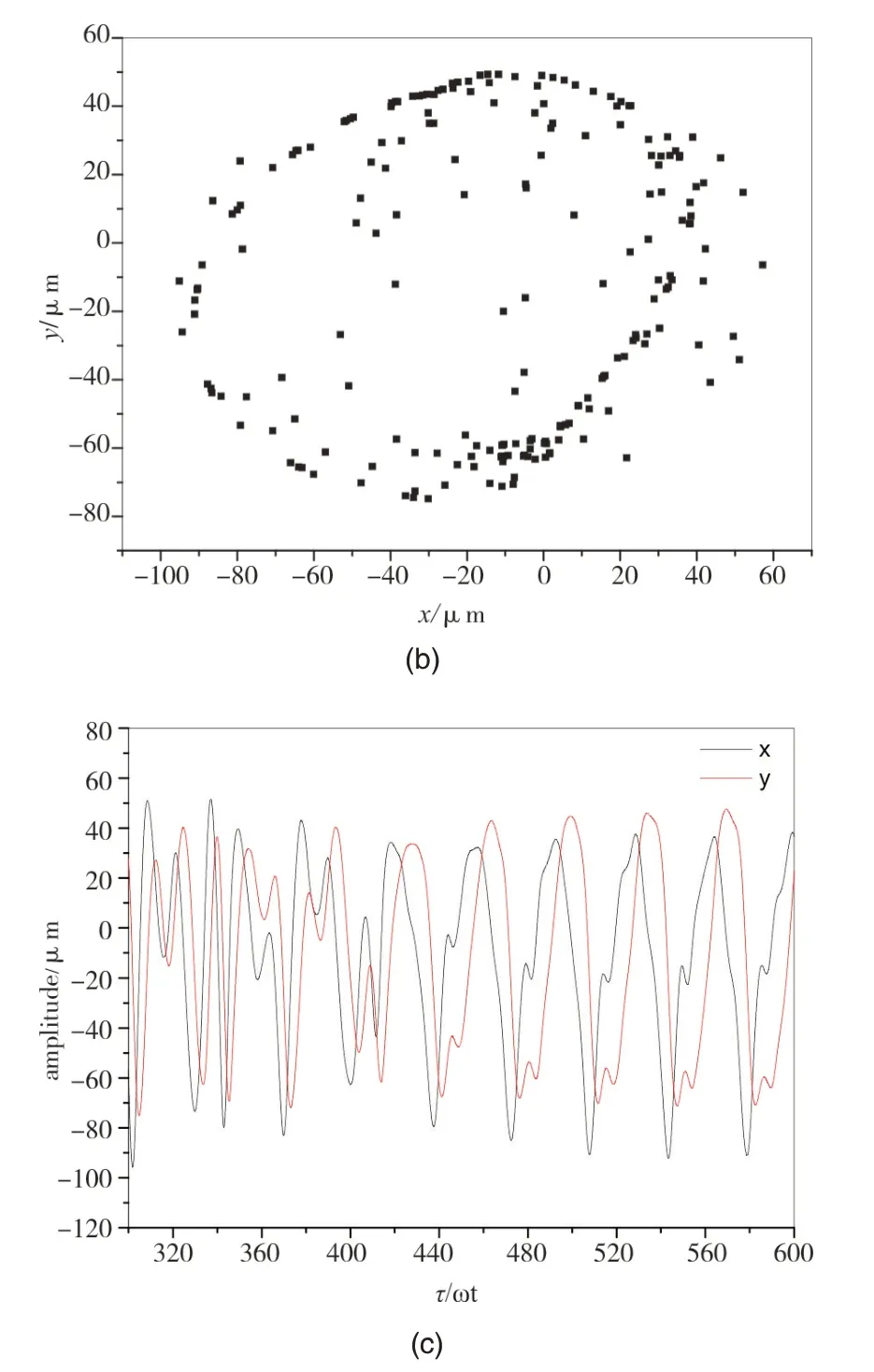
图5 混沌运动Fig.5 Chaotic motion

5 结论

本文针对局部非线性动力系统质量、阻尼和刚度矩阵大型稀疏非对称特点，充分考虑局部非线性力、截断误差等因素，提出了一种二次降维方法及其配套的周期解求解方法，把原高维系统降阶为等价的低维系统，使得系统的维数得到大大降低。整个降阶过程仅在n维系统上进行，第一次降阶不涉及复数运算，第二次降维只需要求解一个低维特征值问题。数值试验表明，本文算法具有比较高的数值精度和收敛精度，有利于认识透平机械非正常工况亚谐和超谐非线性振动。