Research on the Relationship Between Dynamic Behavior of Active Magnetic Bearing System And the Performance of the Auxiliary Bearing*

Zhe Sun Guo-jun Yang Jing-jing Zhao Xun-shi Yan Zhen-gang Shi

（1.Institute of Nuclear and New Energy Technology,Tsinghua University;2.Collaborative Innovation Center of Advanced Nuclear Energy Technology;3.The Key Laboratory of Advanced Reactor Engineering and Safety,Ministry of Education)

Abstract：Auxiliary bearings(ABs)are important backup and safety components in active magnetic bearing(AMB)systems.The performance of ABs significantly affects the reliability,safety,and serviceability of the AMB system and the rotating equipment.Research on the dynamic behavior during the touchdown process is crucial for analyzing the severity of the touchdown and the behavior is closely related to the performance of the AB.In this paper,a friction torque coefficient is introduced to evaluate the performance of AB and the touchdown process is simulated and evaluated with various values of this coefficient with a detailed rotor-AB model of a vertical AMB system.The results show that large friction torque coefficient will result in undesired backward whirl of the rotor and catastrophic large load on the AB.Based on these results, this paper suggests that large friction torque coefficient of AB should be avoided in practice..

Keywords：Active Magnetic Bearing System;Auxiliary Bearing;Rotor Touchdown;Dynamic Behavior;Friction Torque Coefficient

Nomenclature

cTfFriction torque coefficient between inner and outer rings of AB

diInner diameter of ABIR

dRDiameter of the rotor

Fx,FyForces on the rotor inx-andy-direction

Fa,FrAxial and radial forces between rotor and ABIR

Ff,R,Ff,ZRadial and axial friction forces between rotor and ABIR

Fn,RNormal force between the rotor and the AB in the radial plane

Fz,R,Fz,ZAxial forces between the rotor and the AB due to radial friction and axial contact

Jd,JpEquator and polar moment of inertia of the rotor

Ja,JrAxial and radial load integral of the AB

lDistance between the AB and the center of the rotor

mMass of the rotor

qLoad distribution function of the AB

rEccentricity of the rotor

SGDifference between the diameter of the ball and the radii of the raceways

T,TIEFriction torque between the inner and outer rings of the AB,values by empirical formula and actual value

TRRFriction torque between the rotor and the ABIR

TtTransient time

x0,y0,zPosition of the center of the rotor

x,yPosition of the rotor in the radial plane of the AB

αRevolution angle of the rotor

αc,α'cInitial and loaded contact angle of the AB

βRevolution angle of the ABIR

δa,δrAxial and radial deflection of the AB

δmaxMaximal deflection among all balls of the AB

ΔvRelative linear velocity between the rotor and ABIR

εLoad distribution factor of the AB

θSpin angel of the rotor

μFriction coefficient between the rotor and the ABIR

ψx,ψyAngular deflection between the rotor and the axis

Ω Angular speed of rotor spin

sgn Signum function

∗,∗ First and second order derivative of ∗w.r.t time

0 Introduction

Magnetic bearings are widely applied in High Temperature Gas-cooled Reactor(HTGR)[1],where the rotating machineries are running under high purely helium environment.Compared with conventional bearings,Active Magnetic Bearings (AMBs) possess several attractive advantages,such as no friction,no need for lubrication,and the ability of longterm high speed running.Some essential rotating equipments in HTGR are supported by AMBs,e.g.the main helium circulator and the helium blower in the fuel circulation system.The reliability of these equipments,especially in accident condition,plays crucial role in the safety of the whole nuclear plant.At present,the application of AMBs has expanded from special fields such as nuclear power to general industrial fields,especially in the field of fluid machinery [2-4].A thorough summary of applications of AMB in compressors and blowers can be found in Yin et al(2019)[5].

In an AMB system,the rotating rotor is suspended by electromagnetic forces and there is no contact between the rotor and the stator.An AMB system is a complex mechatronic system and consists a large number of structural,electronic components and sophisticated control software.Some abnormal operation condition,for example long-term overload,unexpected impact,slight failure of components,are sustainable and can hardly affect the suspension.However,in the worst case the magnetic suspension might fail and the rotor might touch down.To avoid damage to the rotor and stator during the touchdown process,the so-called "Auxiliary Bearings" (ABs) are necessary in AMB systems.The ABs bears the rotating rotor during the touchdown process.They are important backup and safety components in AMB systems and can be regarded as the "last stand" for the safety of an AMB system.

Research on the dynamic behavior during the touchdown process is crucial for analyzing the severity of the touchdown.Evaluating the contact forces between the rotor and the ABs plays a central role of dynamic analysis of a touchdown process.These forces can hardly be measured directly and should be estimated from the acceleration and velocity of the rotor.

Many remarkable achievements have been accomplished in the literature to estimate the highly nonlinear dynamic process associated with rotor touchdown.In 1991,Ishii and Kirk (1991) [6] built the touchdown model of the Jeffcott rotor,gaining the transient response of the touchdown process by numerical method and obtained the optimal damping to reduce the displacement and contact force.Fumagali and Schweitzer (1996)[7] analyzed the influence of the air gap,friction coefficient,supporting damping and stiffness on the dynamic behavior of rotor’s touchdown process.Fang and Barrett (1996)[8] added the Coulomb friction to Kirk’s mathematical model and gain the transient response using the Newmark-βmethod.In 2003,Zeng (2003)[9]studied dynamic behavior of the rotor drop on to the auxiliary bearing with different supporting condition,found out the critical friction coefficient causing the backward whirling and claimed the low friction coefficient and soft support can reduce the contact force and the possibility of occurring backward whirl.Sun et al(2004),Sun(2006),Lee and Palazzolo(2012)[10-12]considered rotor drop simulation of a flywheel energy storage system,numerically and experimentally.The results suggested therefore that the life of the auxiliary bearing can be extended by reducing auxiliary bearing clearance,dropping velocity,contact friction and support stiffness,applying static side-loads and increasing support.Keogh and Yong (2007) [13] indicated that the rotor drop procedure can be treated as a combination of bounce and rub.They simulated transient thermal response for a series of contact conditions.Moreover,an active recovery strategy was also obtained to make the rotor return from a persistent contact state back to a contact-free state [14].The majority of reported researches involves horizontal rotor drop.However,in vertical rotor drop tests forward whirl is prevalent.Tan et al (2008) [15] built a finite element model of vertical arranged rotor drop on to the auxiliary bearings and got the equivalent stress distribution of the rotor and auxiliary bearings.Zhao et al (2012) [16] used ABAQUS to analyze stress and deformation in auxiliary bearing,however,this paper lacks consideration of the dynamic behavior of the rotor.Xiao et al (2013) [17] analyzed the load character of the ceramic ball auxiliary bearing and established a finite element model in ANSYS applied in transient response of the dropped rotor.However,this work did not consider the friction between the rotor and auxiliary bearing.Sun et al(2014)et al[18]estimated the displacements,velocities and accelerations of the rotor during touchdown from both the dynamic model and noisy data,the dynamic model of the rotor is introduced and Kalman filtering technique is applied,and this result is extended in [19] by incorporating machine learning technique.

Previous theoretical analysis,simulation studies and experimental studies have shown that a vertical rotor system that uses rolling bearings as ABs may exhibit two motion states after touchdown:forward whirl in the same direction as the rotor's rotation and backward whirl in the direction opposite to the rotor's rotation.Under the influence of the gyroscopic effect,the radial support force of the AB on the rotor causes the rotor to make forward whirl;and when the rotor contacts the AB,the rotor receives the tangential friction force opposite to the direction of rotation,which causes the rotor to backward whirl.

In these two whirl states,the relative linear velocity of the contact surface between the rotor and the inner ring of AB (denoted as Δv,see the nomenclature) is zero at steady state,and the friction torque between the two (denoted asTRR) is generated by the static friction force.In the forward whirl state,the two rotate at the same speed.The static friction torque received by the rotor drives the rotor to decelerate.The amplitude of the static friction torque received by the inner ring (ABIR) is slightly smaller than the friction torque between the inner and outer rings (denoted asTIE),which dissipate the overall rotor-ABIR kinetic energy.The two gradually slowed down until they stopped.In the backward whir state,the static friction torque drives the rotor to accelerate,and the ABIR decelerates until its speed is zero.The rotor whirls backwards at high speed in the state of a planetary gear.Because the steady state backward whirl speed is extremely high (about three orders of magnitude higher than the rotor spin speed [20]),in fact,before reaching the steady state,the force between the rotor and the bearing will far exceeded the maximum load limit of the bearing and damages the bearing.

Consider two extreme cases:1)if the friction torque between the inner and outer rings of the bearing (denoted asTIE)is zero,the rotor will permanently maintain whirl of constant speed.2)IfTIE=∞,then the AB is equivalent to a sliding bearing,and the rotor will whirl backwards (assuming that the sliding friction coefficient between the rotor and the inner ring is sufficiently large).Therefore,the friction torque between the inner and outer rings of the bearingTIEis a major factor that determines the state of motion of the rotor after touchdown.In this paper,the friction torque coefficientcTfis used to describe the magnitude of the friction torque,and the influence of the friction torque coefficientcTfon the rotor motion state is mainly investigated.

In this paper,a vertical arranged AMB system with ABs is modelled,the motion equation of the rotor and the load-deflection relationship of the ball bearing are considered.The friction torque coefficientcTfis introduced to evaluate the friction torque between the inner and outer rings of the AB.The motion state of the rotor and the contact force between the rotor and AB are simulated with various values of friction torque coefficientcTf.The results show that forward whirl and acceptable force can be assured with a smallcTfand largecTfwill result in backward whirl with catastrophically large contact force.

1 Analysis model

There are many published works Sun et al (2014)[18],Kang et al (2014) [21] of the vertical dynamic modeling of the touchdown process of AMB systems.The main differences between this paper and the models in these publications are:

1)This paper uses a three-degree-of-freedom model,ignoring the effect of the lower AB,but considering the effect of the gyroscopic effect.According to previous simulations and experimental studies,the contact force between the lower AB and the rotor is relatively small,which has a secondary effect on the rotor's motion state.The radial and axial contact between the rotors and the upper AB is mainly discussed.In the experimental study,it was found that the form of motion after the touchdown is mainly the forward whirl in the same direction as the rotation.The papers [22,20] use cross stiffness to describe the force driving the rotor forward whirl.This paper believes that the main driving force for generating forward whirl is the gyroscopic force,and the AB exerts a normal force on the rotor pointing to the axis of revolution,which causes the rotor to produce forward whirl.

2) In this paper,the internal load analysis of the rolling bearing is used to calculate the relationship between the force between the rotor and the AB and the deflection of the AB,and the coupling of the radial and axial loads is considered.Most of the references use simple elastic contact models.In general application scenarios,the purpose of calculation is to calculate the contact state of the inner and outer rings and rolling elements based on the bearing load,and then to obtain the deflection of the bearing and the stress of each part [23,24].In this paper,the calculation process is reversed.The force between the bearing and the rotor needs to be calculated based on the deflection of the AB.Specifically,the purpose of this article is to simulate the motion state of the rotor.In the simulation process,the calculation process at each step is as follows:the rotor position and speed are known,the contact force between the rotor and the AB is obtained,and the rotor acceleration and angular acceleration are obtained according to the motion equation,and then integrate to attain the rotor position and speed in the next step.The specific calculation process will be given in the next section.

3)This paper considers the motion of the ABIR,and also considers the friction between the rotor-inner ring and the inner ring-outer ring.The ABIR acts as an intermediary part between the rotor and the stator,and its motion state has a great influence on the contact force between the AB and rotor.This paper considers the rotating state of the inner ring,and determines the friction force by the relative motion relationship between the ABIR and the rotor,and between the inner and the outer rings.

4) In this paper,the friction torque coefficient the inner and the outer rings is used as the most important indicator to measure the performance of the bearing.The friction torque between the inner and outer rings of the rolling bearing can usually be calculated by an empirical formula [24,25].The empirical formula is mainly based on the data of the longterm running of the rolling bearing.During the touchdown process,the actual torque may differ greatly from the empirical formula.The possible influencing factors are:1) The cumulative running time of the protective bearing is short,and the state is different from the long-term running bearing.2)The lubrication state is different.3) Repeated touchdowns may cause damage to the ABs and increase the friction torque.For the above reasons,this paper revises the empirical formula,keeping the form of the empirical formula unchanged,but multiplying by a coefficientcTf,and uses this coefficient as the most important indicator to measure the performance of the AB.

The schematic diagram of the analysis objects in this paper is shown in Fig.1.

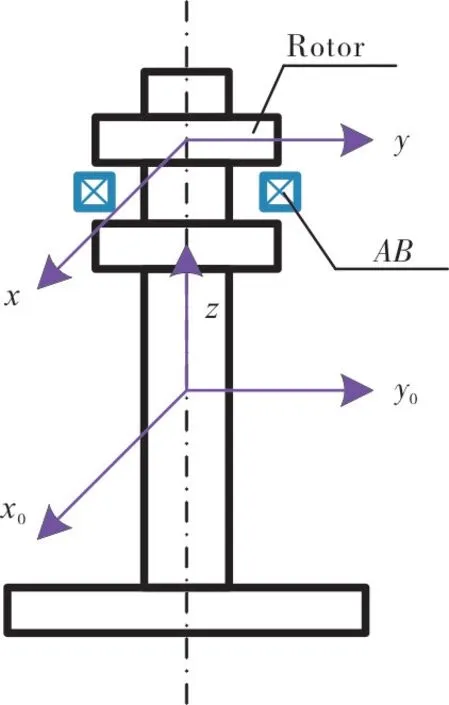
Fig.1 Diagram of the AMB system with ABs

The forces on the rotor and the ABIR are demonstrated in Fig.2.

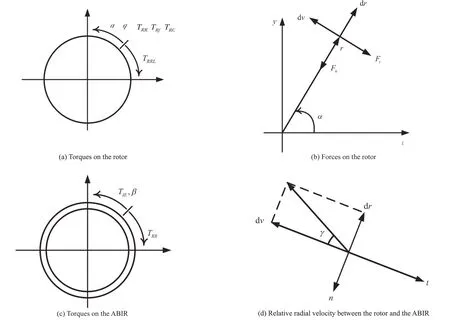
Fig.2 Forces and torques on the rotor and the ABIR

The force on the rotor includes centrifugal force and contact force with the bearing[18].The centrifugal force can be calculated easily and this paper mainly consider the contact force.The rotor motion equation and rotor-bearing interaction equation are as follows:

1) Rotor motion equation:The rotor model considering the gyroscopic effect is as follows:

2)Contact forces between the rotor and the AB

The contact forces are trivially zero when no contact occurs.In the following the case of contact is discussed.

2.1)Counterforce due to deflection of the AB

In the following algorithm the contact forcesFr,Faare calculated with known deflectionsδrand structural parameters of the AB.

a) Solve the loaded contact angleby the following equation[23Chapter 3]

b) Calculate the load distribution factorεby Eq.(10-3)in Okamoto(2003)[23].

c)Calculate the load distribution function and load integralsq,Ja,Jrby Eq.(10-13)～(10-12) in Okamoto (2003)[23].

d)Calculate contact forcesFr,Faby Eqs.(10-35)and(10-37)in Okamoto(2003)[23].

2.2)Damping force

Calculated as by Sopanen(2003)[25].

2.3)Friction forces

The relative velocity between the rotor and the ABIR is

The axial friction force due to cylindrical contact surface friction is

If sliding friction between the rotor and the ABIR occurs,the tangential friction force due to cylindrical contact surface frictionFf,Ris calculated as:

And if the rotor rotates synchronously with the ABIR,there is no relative sliding,and the maximum static friction force in this case is

The actual friction forces should be calculated considering the motion state of the rotor-ABIR combination.

The friction force due to friction in the end plane is

Its direction is opposite to Δv.

3）The friction torque between the inner and outer rings of the AB is

whereTis the friction torque calculated by empirical formula[25,24].

Based on the above equations,the motion of the rotor and the ABIR is simulated by the RK4(5) method [26].In this paper,the model of the AMB system in helium circulator of the 10 MW high temperature gas-cooled reactor is used in the simulations.The detailed descriptions and parameters of this system can be found in[27,1].

Because the rotor has a large rotation speed and a large centrifugal force when the backward whirl occurs,the deflection of the AB actually exceeds the calculation range of the formulas in Okamoto (2003) [23],and further calculation is meaningless.Therefore,the following strategy is adopted:if the rotor makes backward whirl after 0.5s from the touchdown,the simulation is stopped;otherwise,the simulation is performed for 20s.This paper mainly examines the influence of the parametercTfand analyzes the different values ofcTf.The range of value ofcTfis 0.1～ 2,the simulation found that the system shows complex characteristics when it is aroundcTf=0.4,so many values aroundcTf=0.4 are simulated.The initial value of the rotor rotation speed is 5000 r/min=524rad/ s,and the initial values of the remaining state quantities are all 0.

2 Simulation Results and Disscusions

2.1 Direction of whirl

The revolution speed of rotoris the key indicator of the whirl direction.The relationship betweenandcTfis shown in Figure 3.The revolution speedof the whole simulation process and the forward whirl steady (if any) state process is plotted.The whole process and steady state were analyzed separately in the figure.Take the revolution speedas the main variable to measure the state of the rotor.If the forward whirl occurs,the start time of the speed fluctuation range less than 0.02 times its steady state value is defined as the transition timeTt;for backward whirl the transition time and steady data are not defined.The following figure uses "All" to indicate the result statistics of the entire simulation process (0.5s or 20s,depending on the whirl state);"Steady" indicates the result statistics of the steady state(t ≥Tt).

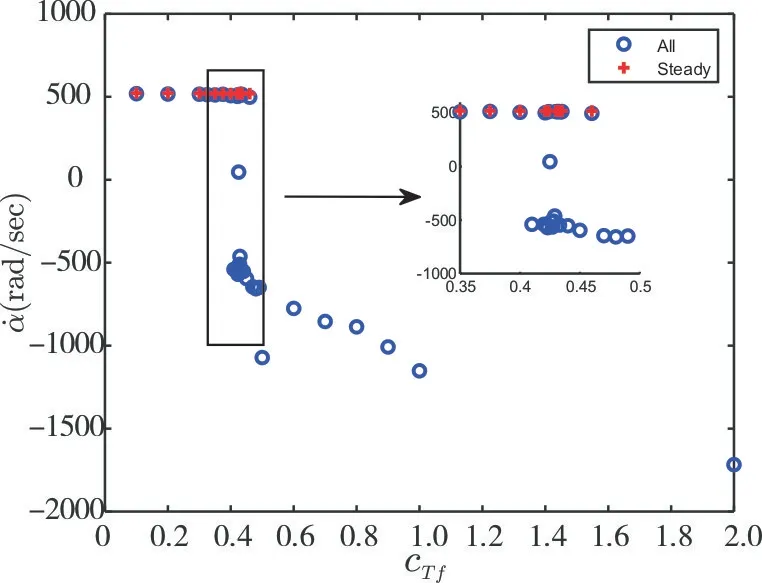
Fig.3 Revolution speed vs.friction torque coefficient cTf

It can be seen from the figure that when the forward whirl occurs,the whirl speedis basically constant,regardless of the coefficientcTf.When backward whirl occurs,increases withcTf.It shows that the forward whirl speed is mainly related to the rotor spin speed,while the reverse whirl speed is closely related to the friction torque.

Forward whirl will occurs whencTf <0.35 and backward whirl occurs whencTf >0.5.For 0.35 ≤cTf≤0.5,there is no definite relationship between the whirl direction andcTf(see upper right small diagram in Figure 3).It shows that in this range,it is in the critical state of forward and backward whirl.At this time,there is a certain randomness in the touchdown process,and the final whirl state may be related to the initial value of the position and velocity at the moment of touchdown.

The orbits of the rotor in the cases ofcTf=0.1 andcTf=2 are shown in the Figure 4,and the unit is mm.In both cases,the orbits of 0.05s after the touchdown are plotted,the steady-state(19.95～20s)orbit is plotted in the casecTf=0.1,and the 0.45-0.5s orbit is plotted in the casecTf=2.The red dotted line at 0.19mm represents the measured gap between the rotor and the AB.When the orbit exceeds the red dotted line,the rotor invades the AB.The red arrow indicates the direction of rotor whirl.It can be seen that with different values ofcTf,the orbits within 0.05s after the touchdown are basically the same,and several rub-impact have occurred.But after entering the steady state,the whirl directions of the two are obviously different.In the case ofcTf=2,the deflection of AB has reached more than 0.3mm,which may actually cause damage to the bearing.

2.2 Normal forces on the AB

The varying processes w.r.t time of the normal force on the AB with variouscTfare illustrated in Figure 5.

As shown in the figure,the largercTfis bearing normal force.WhencTf >0.5,the bearing normal force increases rapidly w.r.t time,because whencTfis very large,the rotor quickly enters the backward whirl state,and the magnitude of the revolution angular velocity increases rapidly as well.ForcTf=2 the bearing normal force has exceeded 800kN at 0.5s,and the bearing is likely to be damaged.

It can also be seen from the figure that when forward whirl occurs with smallcTf,the bearing normal force is large within a few seconds after the touchdown,and then decreases significantly.The reason is that after the touchdown,the rotor first repeatedly rubs and impacts the ABIR.During this period,the contact force is large.After a few seconds,the rotor and the ABIR are relatively stationary.The two jointly make a forward whirl,and the normal force is equal to the centrifugal force and has a relatively small amplitude.Therefore,the time after the touchdown is divided into three sections of 0～0.5s,0.5～5s,and 5～20s,and the maximum bearing normal force in the three periods is plotted as shown in the Figure 6.Note that for the cases with backward whirl,only 0.5s is simulated,so there is no data in the last two segments.

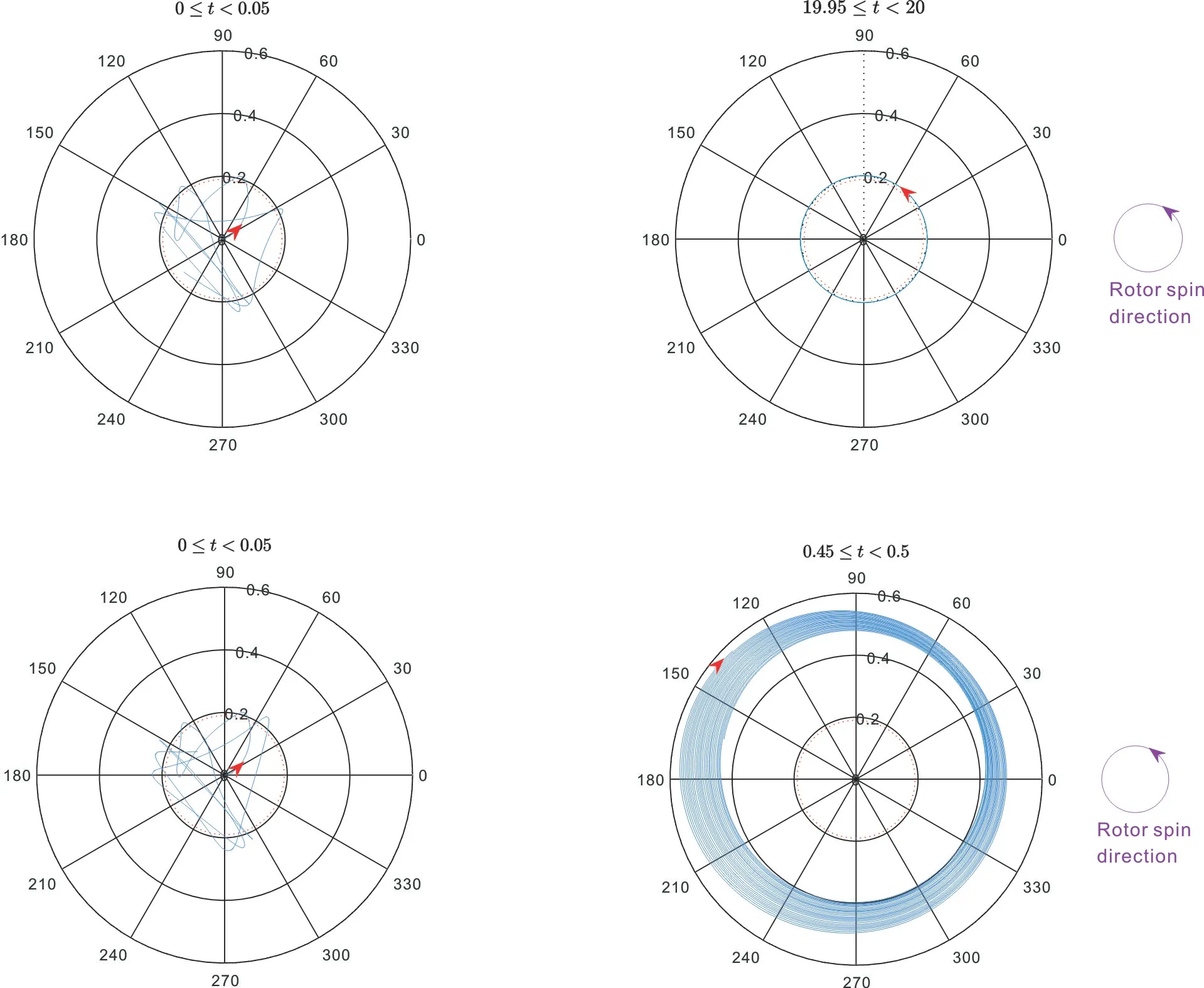
Fig.4 Orbits after touchdown with cTf=0.1 and cTf=2

Fig.5 Normal force on the AB w.r.t time and cTf

Fig.6 Maximal normal force in various time interval with various cTf

The red dotted line in the figure indicates the rated dynamic load of the AB.The figure also shows again that whencTfis small,the maximum normal force appears within the first 0.5s after the touchdown.WhencTfis large,the maximum normal force has already exceeded the rated dynamic load of the AB,which may cause AB damage within a very short time.According to the simulation results,whencTf <0.325 the maximum normal force does not exceed the rated dynamic load,the AB can withstand multiple touchdowns;whencTf >0.5 the maximum normal force exceeds the rated dynamic load,the AB may be damaged in a short time.At that situation with 0.325 ≤cTf≤0.5,the system characteristics are more complicated and may be affected by other factors.In some cases,the rotor will make chaotic irregular motion for a long time without entering a steady state.The change trend of the tangential force and axial force of the bearing is similar to the normal force,but the tangential force and axial force are relatively small and will not be discussed here.

2.3 Axial motion of the rotor

The axial motion of the rotor withcTf=0.1 andcTf=2 is illustrated in Figure 7.

Fig.7 Axial motion of the rotor with cTf=0.1 and cTf=2

It can be seen that with variouscTf,the trajectories of first few bounces (within 0.05s) are basically the same,and the radial contact between the rotor and the AB has not yet dominated.When the radial contact force between the rotor and the ABIR is large,the radial contact affects the axial motion.Specifically,whencTf=2 the rotor's radial contact force is large,a huge axial friction is generated,which limits the rotor's axial bounce,so the number of the axial bounce with is less;the axial force is reduced due to the radial friction,thus the steady-state axial position withcTf=2 is slightly higher than the casecTf=0.1.

2.4 Discussions on simulation results

To sum up,for the simulation model in this paper,forcTf <0.325 forward whirl occurs and the normal force on the AB does not exceeding the rated dynamic load;when 0.325 ≤cTf <0.35 the forward whirl occurs as well.In the first 0.5s after the touchdown the normal force is slightly greater than the rated dynamic load of the bearing;whencTf >0.5 backward whirl occurs,the normal force of the bearing will quickly exceed the rated load of within a very short time after the touchdown,causing damage to the bearing;There is no definite relationship between the direction of movement andcTfwhen 0.35 ≤cTf≤0.5,indicating the critical state of forward and backward whirl.The specific motion state is affected by other factors.Depending on the state,when the backward whirl or chaotic motion occurs,the bearing force will exceed the rated load.

3 Conclusions

In this paper,the touchdown process of vertical AMB system is simulated,the effect of the AB performance on the dynamic behavior is investigated.Compared with the previous works,the modeling method in this paper has the following characteristics:1) The gyroscopic effect of the rotor is considered;2) The internal model of the AB is used to analyze the relationship between the external bearing load and the deflection of the protective bearing;3)The motion of the ABIR is considered,and the friction relationship between the rotor-inner ring and the inner ring-outer ring is considered;4)The friction torque coefficient between the inner ring-outer ringcTfis used as the most important indicator to measure the performance of the bearing.

This paper verifies again through analysis and simulation that the form of whirl after the rotor touchdown is the most important factor in determining the load of the AB.The analysis in this paper points out that for vertical rotors,the gyroscopic effect is the main factor that causes forward whirl after touchdown.Through the simulation of various value of friction torque coefficientscTf,it is found that whencTf <0.35 the forward whirl occurs,the bearing normal force is within the acceptable range;whencTf >0.5 the backward whirl occurs,the bearing normal force far exceeds the rated load.The case with 0.35 ≤cTf≤0.5 is a critical state,the rotor motion state and bearing force are related to other factors.

The research in this paper shows that for the vertical AMB system,under the conditions that other structures are determined,reducing the coefficient of friction torque of the AB is the main means to prevent the catastrophic backward whirl of the rotor.For the actual AMB system,it is very necessary to dismantle and examine the AB in daily maintenance.The friction torque coefficient can be used as an important reference index to determine whether the AB needs to be replaced.In addition,the estimation of the friction torque coefficient based on the touchdown data is also an important part of the monitoring of the health status of the AB system.The modeling and analysis in this paper can provide a basis for the estimation of the friction torque coefficient.

The research of this paper has an important reference value for the deep understanding of its quantitative relationship and internal mechanism of the effect of AB performance on the touchdown process and has an important guidance for the design,monitoring and maintenance of the actual AMB system.The future works of this paper include:1) adding a complete five-degree-of-freedom analysis,and considering the different contact states of the rotor and the ABIR[27];2)considering the effect of the defect state of the internal parts of the rolling bearing on the friction torque coefficient;3)modeling and simulation of other forms of ABs.