角接触球轴承的罚函数粒子群算法优化设计

胡启国，杜春超，吴明钦，杨学蛟，曹历杰

(1. 重庆交通大学，机电与车辆工程学院，重庆 400074； 2. 川庆钻探工程公司 安全环保质量监督检测研究院， 四川 广汉 618300)

0 引 言

双列角接触球轴承被广泛运用于旋转机械中，高效、安全运行能直接保障系统的正常运行，因此开展双列角接触球轴承优化研究具有一定的意义。

目前，很多学者对轴承进行了研究，分别从轴承的结构、失效机理和可靠性[1]等方面出发，考虑不同因素对轴承性能的影响。轴承结构复杂，优化参数能使轴承具有更好的性能。黄鹏等[2]以单位承载能力下总功率损失最小作为优化目标函数，采用粒子群优化算法对磨床砂轮主轴静压轴承进行优化，明显改善了轴承的综合性能；冯吉路等[3]提出以轴承最小生热率为优化目标函数，采用Kriging算法和粒子群算法(particle swarm optimization，PSO)相结合的混合算法对轴承的结构参数进行优化，取得了较好的设计结果，提高了设计效率；考虑粒子群算法在目标函数比较复杂时，其容易陷入局部最优解，尤其是当目标函数存在多峰极值时，更易陷入局部最优的情况，徐向阳等[4]提出了一种改进自适应权重PSO算法，并利用惩罚函数处理约束问题，对行星齿轮传动系统进行多目标优化设计，结构参数优化后具有更高的传动效率；李奇等[5]提出多目标优化方法，采用改进粒子群算法对混合动力系统重量和体积的多目标优化参数匹配计算，得到了最优解；罗天宇等[6]推导了角接触球轴承的轴向刚度计算公式，并以轴承刚度为目标函数进行优化，结果表明，在满足寿命的前提下，适当增加滚珠直径减少滚珠数量；程超等[7]建立了双列角接触球轴承结构优化的数学模型，采用免疫算法对其主要结构参数进行优化设计，并通过遗传算法对比分析，其优化结果优于遗传算法。利用传统粒子群算法进行结构参数优化，粒子向个体最优位置、全局最优位置移动的速度较缓慢，影响寻优效率，且当存在多目标优化问题时，传统粒子群优化算法易陷入局部最优解等问题。

因此，笔者采用罚函数改进粒子群算法，以轴承额定动载荷和额定静载荷多目标函数，对双列角接触球轴承结构主要参数进行优化设计。首先，建立轴承多目标优化数学模型，采用线性加权和法，解决粒子群算法在处理多目标优化问题上的缺陷；其次，在PSO中引入粒子随机衰减因子，加快收敛速度，提高算法的全局搜索能力。最后，引入罚函数来处理约束问题，较好地实现了轴承优化设计，使额定动载荷和额定静载荷得到了较大提高。

1 轴承优化数学模型的建立

在滚动轴承服役过程中，高额定静载荷能改善轴承的承载能力和运行平稳性，能有利于延长轴承的疲劳寿命。因此，寻求轴承最优结构参数过程中，不仅要考虑轴承的动载荷疲劳失效，还需要考虑静载荷不足引起的塑形变形失效，提高轴承承载能力和抗冲击载荷的能力。

1.1 目标函数

轴承的优化设计是在不改变轴承装配尺寸下，建立优化目标函数，通过求解目标函数，得到最优的轴承参数组合。笔者以基本额定动载荷和基本额定静载荷为轴承优化设计的目标函数。

轴承的额定动载荷公式[8]如式(1)：

(1)

式中：bmov为动载系数；轴承列数l=2；接触角α=30°；Z为单列滚珠数；dg为滚珠直径；fc为其它相关系数(轴承类型、几何参数等)，其一般表达式[9]为：

(2)

式中：γ为几何参数，γ=dgcosα/Dgp；Dgp为滚珠的节圆直径；fi、fe分别为内、外滚道沟曲率半径系数。

当轴承滚珠直径大于25.4 mm时，式(1)不再适用于计算轴承的额定动载荷。根据美国国家标准协会(ANSI)的推荐，球径dg的幂指数由1.8改为1.4。而本研究中的球径均未超过25.4 mm，根据式(1)计算是合理的。

由轴承设计理论和相关经验可知，轴承内滚道和滚珠的接触应力通常大于轴承外滚道和滚珠的接触应力。因而以内圈和滚动体的接触应力来确定球轴承额定静载荷，轴承的基本额定静载荷计算公式[9]如式(3)：

(3)

轴承在使用时对轴承的额定动载荷和额定静载荷均有要求，只是在具体实际问题中所占的权重各不一样。因此以C1为优化对象，其表示额定动、静载荷的加权和，表达式为：

C1=β1C+β2Co

(4)

式中：β1、β2分别为C和Co的加权系数，满足β1+β2=1。

滚动体和内圈的曲率差[9]计算如式(5)：

(5)

式中：ρⅠ1表示滚动体表面接触点的第Ⅰ主曲面曲率；ρⅠ2表示内圈滚道表面接触点的第Ⅰ主曲面曲率；ρⅡ1表示滚动体表面接触点的第Ⅱ主曲面曲率；ρⅡ2表示内圈滚道表面接触点的第Ⅱ主曲面曲率；∑ρ表示曲率和。曲率和∑ρ计算公式如式(6)：

(6)

在多目标优化问题中，各优化目标之间往往会相互矛盾。由式(1)～(3)可以看出，滚珠直径和个数对轴承的额定动载荷和额定静载荷影响各不相同，滚珠直径对于轴承的额定动载荷影响较大，而滚珠个数对于轴承的额定静载荷影响较明显。因此，为了同时提高轴承的额定动载荷和额定静载荷，必须要在滚珠的大小和个数之间作出折中。

1.2 设计变量

轴承的结构参数主要包括fi、fe、Z、dg和Dgp，将上述参数作为优化设计变量，如式(7)：

X=[x1,x2,x3,x4,x5]=[fi,fe, Z,dg,Dgp]

(7)

1.3 约束条件

轴承的主要参数优化变量应该满足如下条件：

1)滚道沟曲率半径约束

滚道沟曲率半径系数与轴承轴径向刚度、游隙、接触角、摩擦力矩和保持架滑动率等密切相关，是影响轴承动态性能的重要结构参数。文献[10]指出，曲率半径取值应满足小于0.535dg的条件。所以，约束条件如式(8)：

(8)

对于沟曲率半径小于0.515dg的轴承设计，通常只要对其它4个结构参数进行优化设计即可。

2)滚珠直径约束

Kg,min(D-d)/2≤dg≤Kg,max(D-d)/2

(9)

式中：Kg,min为直径约束最小值；Kg,max为直径约束最大值；D为外径；d为内径。滚珠直径约束条件为：

(10)

3)保持架力学性能约束

为了使轴承具有较好的力学性能，应保证轴承内部滚珠数量，但保持数量充足的同时会造成保持架过梁宽度之间的矛盾。因此，对保持架进行约束条件如式(11)[10]：

u5(X)=πDgp-1.05dgZ-Zbmin≥0

(11)

4)滚珠组节圆直径约束

为了保证轴承运行过程的旋转灵活度，滚珠组节圆直径与轴承平均直径的差值不宜过大。因此，进行优化设计时，节圆直径应大于轴承平均直径，约束条件为：

(12)

5)外圈壁厚约束

参考轴承设计标准，轴承外圈沟底壁厚度应大于ξdg，其中，ξ为常数。约束条件如式(13)：

u8(X)=(D-Dgp-dg)/2-ξdg≥0

(13)

综合以上分析及约束，可以得出角接触球轴承主要参数设计多目标优化模型：

(14)

式中：f1(X)、f2(X)为第一、第二优化目标。

2 计算方法和程序

2.1 粒子群优化算法

标准PSO算法在每次迭代过程中，粒子个体和群体之间的位置和速度按照式(15)进行更新：

(15)

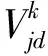
在PSO中，惯性权重ω为关键参数，较大的ω全局搜索能力增强，局部搜索能力降低，反之亦然，通过控制ω可以调整全局和局部搜索能力。在自适应粒子群算法中，ω为变量，是进化代数的减函数，ω随着进化代数的增加而线性递减，即：

(16)

式中：Tmax为最大迭代次数；t为当前迭代次数。

通过对PSO算法进行改进，增加随迭代次数改变的粒子随机衰减因子α、表示收敛速度快慢的参数β和表达更新常数μ，同时赋予其初始状态参数值[5]，其中α可以表示为：

αk+1=αk·μ,α∈[0,1]

(17)

即每次迭代过程的α值满足μ倍等比关系。

改进粒子位置的更新过程为：

(18)

式中：r为随机数；S为取值区间大小。

2.2 惩罚函数

惩罚函数作为目前主要的约束优化处理方法之一，其核心思想是将约束优化问题转化为无约束问题来求解，对不符合约束条件和试图穿越约束边界的非可行点予以惩罚，使其往可行域靠近。其构造思想是在原目标函数中加入惩罚项，从而得到一个增广目标函数，由此将约束优化问题转化为无约束优化问题。

对于优化问题〈A，f〉中，A为约束条件的可行解，f:A→Rn为目标优化对象，所以得出目标对象minf(x)求解表达式：

(19)

式中：Gj(x)≥0(j=1,2,…,m)为约束条件，其中，约束Gj(x)≥0与min[0,Gj(x)]=0等价。所以，可进行约束问题的等价替换，得出：

minf(x),x∈Rn

(20)

s.t. min[0,gj(x)]=0,j=1,2,…,m

(21)

(22)

式中：F(x,M)为惩罚函数；M为惩罚因子，是非负常数；Mp(x)为惩罚项；p(x)为惩罚函数。只要M值较大，则F(x,M)的最优解与约束问题的最优解相近。因此，将求解约束极值的问题转化为求解无约束极值问题。

2.3 罚函数粒子群算法基本步骤

根据标准粒子群算法原理，采用惩罚函数处理角接触球轴承优化设计中的约束条件，确保其目标函数的解在合理区间内，提高求解精度，罚函数粒子群算法的优化流程如图1。

图1 PSO算法求解流程Fig. 1 PSO algorithm solution flow chart

具体步骤如下：

Step 1粒子群初始化：粒子数N，学习因子c1和c2，最大权重ωmax，最小权重ωmin，最大迭代次数Tmax，罚因子M等，随机生成粒子种群。

Step 2根据惩罚函数惩罚，用随机性衰减因子α增加粒子在边界区间的随机性。

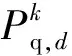
Step 4根据式(16)更新惯性权重ω，采用新的惯性权重ω得到当前粒子位置和速度。

Step 5判断更新后粒子的位置是否满足约束条件，若不满足要求则返回Step 2，反之则以更新后的位置作为全局最优。

Step 6运行至设定的最大循环次数Tmax，得到全局最优结果。

3 算例分析

3.1 罚函数粒子群算法求解

为了验证笔者提出的罚函数改进粒子群算法的可行性，选取型号为3210的角接触球轴承，开展以额定动、静载荷为目标函数的优化分析。轴承内、外径分别为50、90 mm。约束条件相关系数为bmin=0.1dg,Kg,min=0.45，Kg,max=0.6，ε=0.55，ξ=0.3。

罚函数粒子群算法的控制参数有粒子群大小N=20，学习因子采用标准值c1=c2=2，最大权重ωmax=0.9，最小权重ωmin=0.4，且最大迭代次数Tmax=150，α=0.2，β=0.2，μ=0.95，惩罚因子M=1015。图2 为3210轴承基于罚函数粒子群优化算法的适应值优化曲线。

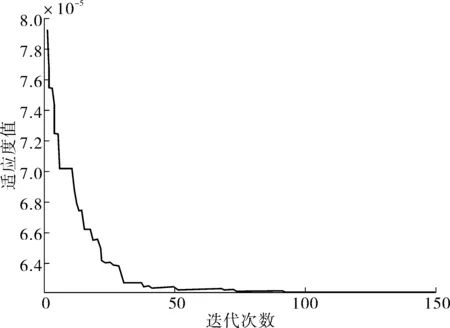
图2 3210轴承适应度优化结果Fig. 2 3210 bearing fitness optimization results

笔者采用迭代次数为程序终止条件。由图2可知，当迭代次数达到50次时，优化结果曲线开始收敛并逐渐趋于稳定，算法程序还未迭代到给定的迭代次数，优化设计结果曲线就已经收敛。由图2还可以看出，其收敛速度快且稳定，体现了该算法的优越性。优化后的轴承设计变量参数如表2。

表2 罚函数粒子群算法优化后设计变量值Table 2 Design variable values after penalized function particle swarmoptimization algorithm

从表2可以看出，经PSO优化后的设计参数满足轴承设计标准，轴承内、外径均满足标准化系列推荐值，同时也满足约束条件，符合轴承设计要求。

将优化后所得的结构参数带入式(2)，得到：

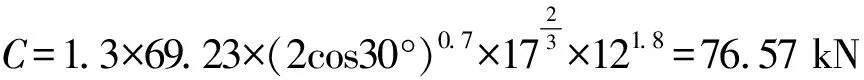
将结构参数带入式(5)，得到：

通过查阅滚动轴承设计手册，3210轴承的额定动载荷为46 kN，额定静载荷为46.8 kN。显然，经过改进粒子群算法优化后的轴承的额定动载荷和额定静载荷显著提高，额定动载荷提高了66.46%，额定静载荷提高了70.60%。

3.2 遗传算法和免疫算法求解

为了进一步验证所提出的罚函数粒子群算法的优化效果，分别采用遗传算法[14]和免疫算法[7]对3210角接触球轴承进行优化验证，最终得出优化结果如表3。

表3 遗传算法和免疫算法优化后设计变量值Table 3 Design variable values after genetic algorithm and immunealgorithm optimization

将这两种算法所得的优化设计参数代入式(1)和式(3)，经计算可到得到轴承的额定动载荷和额定静载荷，表4列出了3种算法的优化计算结果。

由表4可知，经过罚函数粒子群算法优化后的结果显著提高，其中相较于遗传算法，分别提高了2.081、0.17 kN；相较于免疫算法，额定静载荷提高了3.14 kN。经过优化对比，结果表明，罚函数粒子群优化算法的优化效果优于两种算法。

表4 各优化算法目标函数值结果对比Table 4 Comparison of objective function values ofvarious optimization algorithms kN

4 结 论

1)综合考虑影响轴承性能的多种因素，以轴承几何结构参数为优化设计变量，综合考虑设计变量约束条件，建立了轴承优化数学模型。

2)提出了一种用于提高角接触球轴承性能的罚函数粒子群算法，针对传统粒子群算法易于陷入局部最优解和无法处理带复杂约束条件的缺点，以3210角接触球轴承为例，以其额定动载荷和额定静载荷为目标进行优化设计。结果表明，优化后的的额定动、静载荷分别提高了66.46%和70.60%。

3)采用遗传算法和免疫算法对3210角接触球轴承进行了优化设计，验证了所提出的罚函数粒子群算法的优化效果。结果表明，采用罚函数粒子群算法能较好地提高角接触球轴承的性能。