动态环境下的移动机器人避障策略研究

余腾伟，刘昌力

(1. 重庆交通大学 交通工程应用机器人重庆市工程实验室，重庆 400041；2. 重庆嘉陵华光光电科技有限公司 技术开发部，重庆 400700)

0 引 言

移动机器人的路径规划是指在给定的地图环境或者根据不断探测到的障碍物信息下找到一条从起始点到目标点的一条无碰撞的安全行进路线，其本质是在几个约束条件下得到最优或者可行解的问题[1]。根据移动机器人对环境信息的不同获取情况，路径规划算法主要划分为全局路径规划和局部路径规划两类算法[2]。全局路径规划算法一般在环境信息大部分已知的情况下得到广泛应用。近年来的研究中全局的路径规划算法包括蜂群算法、遗传算法、快速随机搜索树算法、拓扑法等。局部路径规划一般应用于移动机器人对环境信息局部未知或完全未知的情况下，其大部分情况下只能在短时间内有效。根据适用情况的不同，局部路径规划算法大部分采用了人工势场法、A*算法和模糊算法等[3]。

基于大部分移动机器人的工作环境，全局、局部路径规划算法的融合是目前研究的一个重点方向。在不同情况下常见的融合方法有两个大的分类：基于行为的混合路径规划方法与基于全局引导的混合式路径规划方法[4]。前者主要将路径规划看作两个并列的模块，在进行全局路径规划和局部路径规划时交替使用，是两个并列的模块；后一种方法则是在先验地图上使用全局路径规划算法求出一条可行的路径，然后移动机器人在该路径上进行实时的动态避障。

目前现有的每个路径规划算法均有不同的缺点，在实际环境下的使用中适用性并不高。笔者针对人工势场法所存在的缺陷对其进行改进。

人工势场法是一种局部路径规划算法，具有计算量小、响应迅速、适用性高等优点，但在实际问题的应用中，易陷入局部最小值导致移动机器人无法抵达目标点的问题。针对该算法的缺陷，国内外许多学者提出了数种解决方案。汪首坤等[5]运用几何法与人工势场法相结合来解决传统人工势场法的局部极小值问题，但该种方法在路径规划时运用了逆运动的方法，需从8组解中进行筛选，计算效率较低；姬伟等[6]引入了虚拟目标点的概念，建立新的移动向量将移动机器人从局部最小点引导出去，从而解决了该问题。但利用几何的方法确定虚拟目标点在较为复杂的环境中适用性较差。

基于各种分析与归纳，目前针对人工势场法的主要改进思路为建立虚拟目标点作为引导、增加虚拟障碍物、建立等势线等方法[7]。因此，笔者参考了各种改进方法的缺点，从建立虚拟目标点的思路出发，结合改进快速扩展随机树算法，使移动机器人能够适应动态环境变化并更好地解决了人工势场法中的局部极小值问题，让移动机器人满足路径规划的要求。

1 人工势场法

1.1 传统人工势场法

人工势场法的本质是对移动机器人工作环境的一种抽象描述，该方法将移动机器人、目标点、障碍物看做质点，进而在移动机器人的工作空间中人为构造一种虚拟势场[8]。虚拟势场由两种势场组成，一种是目标点产生的引力势场，另一种是由障碍物产生的斥力势场。引力势场具有负势能，移动机器人具有向低势能方向移动的趋势；斥力势场具有高势能，移动机器人会优先向低势能方向移动而避开高势能区域。移动机器人的路径规划是进行二维平面空间下的路径规划，但人工势场是表现为三维的，由引力势场所引起，这也是移动机器人在路径规划中的主要驱动力。在图1中目标点所代表的“低谷”具有低势能，对移动机器人产生吸引力；而每个障碍物均会构成一座“高山”，在这些区域中具有高势能，移动机器人所具有的动能无法靠近这些高斥力势能区域，使得移动机器人在进行路径规划时会避开这些障碍物。这种避障策略的思路非常巧妙且具有实用性。

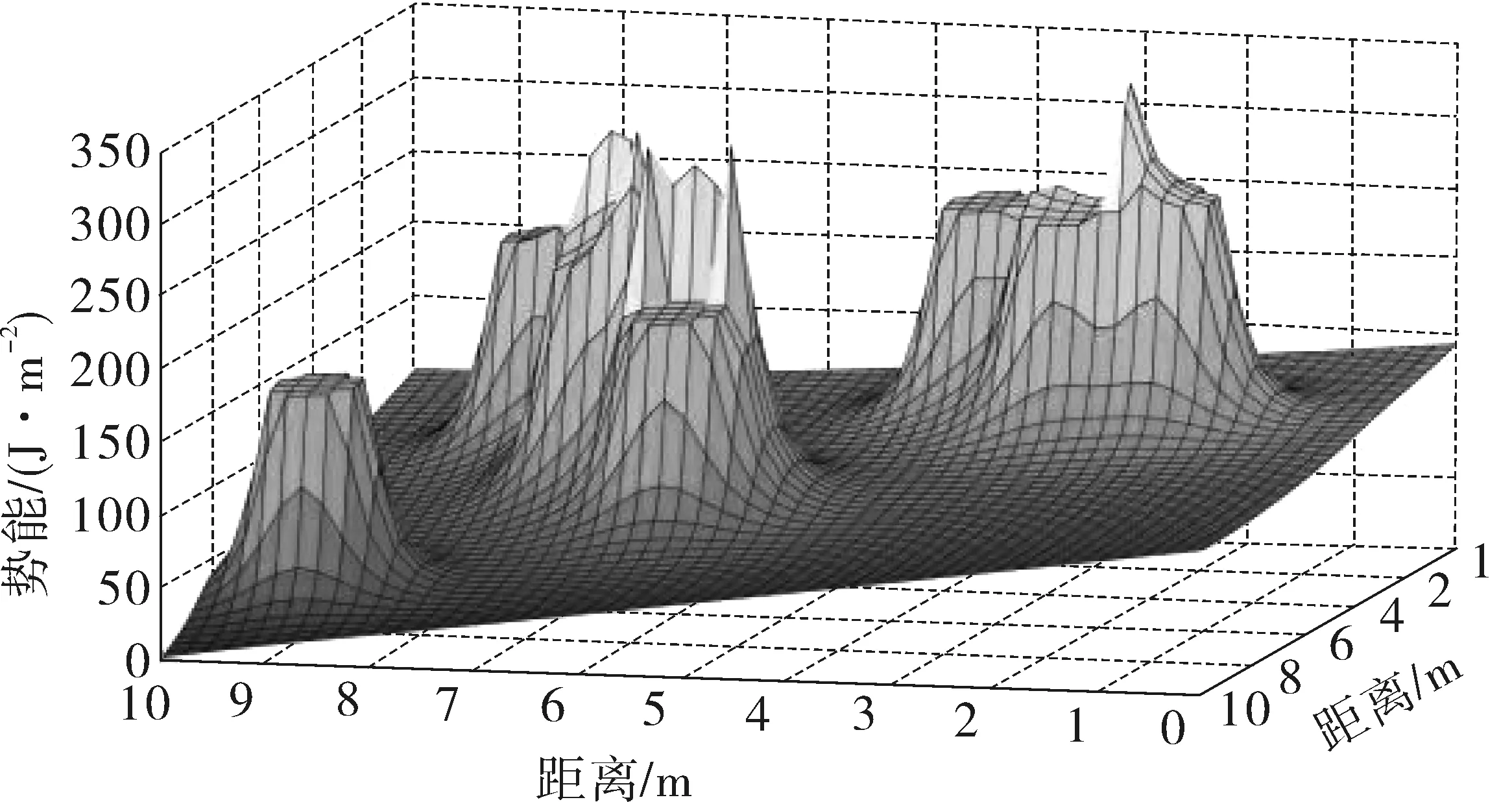
图1 人工势场法三维模型Fig. 1 3D Model of artificial potential field algorithm

传统的人工势场法中只会考虑到移动机器人与障碍物、目标点之间的距离因数。移动机器人与目标点所产生的引力势场与两者之间的距离成正比，与目标点越远，目标点对移动机器人产生的引力越强。引导移动机器人到达目标点，目标点所产生的引力势场作用于全局域。障碍物与移动机器人之间的斥力势场成反比关系，这些障碍物所组成的势场仅作用于局部域，只有在移动机器人进入斥力势场作用域内后才会对规划路径产生影响，规避掉障碍物来达到避障的目的。移动机器人与障碍物、目标点之间的引力斥力关系如式(1)、式(2)：

(1)

(2)

式中：k为引力势场增益系数；m为斥力势场增益系数，通常m≥2；‖pr-pg‖为机器人的实时位置相对于最终目标点的欧几里得距离；p=‖pr-po‖为移动机器人相对于障碍物的欧几里得距离；po为势力场中障碍物对移动机器人产生斥力的距离条件，即当移动机器人与障碍物的距离大于po时不受障碍物产生的斥力势场影响，反之则受到斥力影响。引力Fatt与斥力Frep可由相对应的势场函数求得，分别为：

Fatt(p)=-grad[Uatt(p)]=-k‖pr-pg‖

(3)

Frep(p)=-grad[Urep(p)]=f(x)

(4)

(5)

Ftotal=-∇U=Fatt+Frep

(6)

人工势场法具有计算量小、路径规划轨迹平滑、实时性高等优点，但也存在易使移动机器人陷入局部极小值点的问题，在复杂环境下的实际应用受到较大的局限，动态规划也受到一定影响。

1.2 传统人工势场法的改进思路

动态障碍物的分布存在不确定性和实时性，部分特定的静态障碍物分布情况也会使移动机器人在进行路径规划时遇到某些区域，如图2。区域内障碍物对移动机器人产生斥力Frep与目标点产生吸引力Fatt大小趋近于0，方向相反，此区域被称为局部极小值区域。当移动机器人陷入该区域内时将无法脱离出去，导致路径规划失败[9]；当存在复杂的障碍物，如U型障碍物时，移动机器人被障碍物环绕无法逃出，亦将导致路径规划失败[10]。

图2 局部极小值点问题Fig. 2 Local minimum point problem

国内外学者对如何解决局部极小值问题提出了多种改良方法，比如改进势场函数减少局部极小值点；添加启发式搜索算法等方法。笔者针对这一问题，提出了结合快速扩展随机树算法的方法，在起始点至目标点之间的可行路径上增加临时目标点，解决路径规划对象在局部极小值点附近徘徊震动的问题。

人工势场法在解决路径规划问题时由于缺少全局信息，且移动机器人所面临的环境是未知、动态且复杂的，引入快速扩展随机树算法为其增加数个虚拟目标点的改进方法可在不过多增加计算量的前提下有效提高移动机器人使用人工势场法进行动态路径规划的适用性。

2 快速扩展随机树算法

2.1 快速扩展随机树算法

快速扩展随机树算法最早由La Valle于1998年提出，是一个有效的树类数据结构和随机采样方案，如图3。该算法结合了随机路径规划理论，设定移动机器人的起始点为根节点出发，通过在可行自由空间内生长出一颗扩展随机树的方法来选定一条路径。在生长过程中，随机选取新的节点，直至到达目标点。基本的快速扩展随机树算法包括两个阶段：

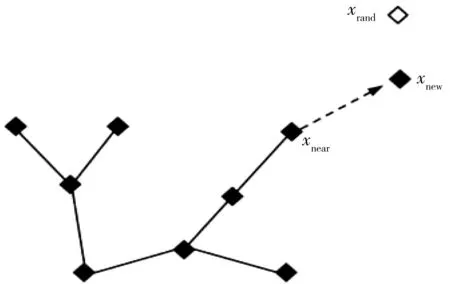
图3 快速扩展随机树扩展示意Fig. 3 Expansion schematic of rapidly exploring random tree

1)构建扩展随机树阶段。在工作空间中通过迭代的方式，每一次均在空间中随机选取一个不属于扩展树的随机节点xrand，随后在扩展树中找出一个与xrand度量最近的节点xnear，再在xnear与xrand的连线上寻求一个新的状态节点xnew，xnew与xnear间的距离满足扩展随机树的扩展步长条件。在此过程中，度量最近的节点xnear向随机节点xrand的方向递增了一个扩展步长的距离，同时需要保证xnew不与障碍物发生碰撞。重复上述的过程直到新的节点包含于目标点内后，结束迭代并构成完整的扩展随机树。

2)路径查询阶段。在完成扩展随机树的构建后，停止再添加进新的节点。根据上一阶段所构造出的扩展随机树，从目标节点开始，逆向搜索整个随机树，层层迭代至起始根节点，计算出一条包含起始根节点与目标节点的路径，且该路径不与障碍物发生碰撞，满足全局路径规划要求。

2.2 改进的快速扩展随机树算法

快速扩展随机树的具体扩展类似于不断生长向四周发散的树，由于其随机性，不可避免的存在扩展太过平均，导致所得到的路径质量不高的问题。笔者针对此问题，提出了一种改进的扩展随机树算法，使随机树的生长朝向目标点，以提高搜索的效率。

改良后具体的算法描述如下：

Step 1在自由空间中确定起始根节点xpstart和随机选取的节点xprand，并判断起始根节点不在障碍物内且随机选取的节点不在扩展随机树内。

Step 2在扩展树中找到xpnear，节点xpnear是扩展树中距离xprand最近的一个点。

Step 3在xpnear与xprand的连线上求解出xpnew，xpnew必须在路径规划区域的自由空间内且与xpnear的距离为扩展随机树的扩展步长。如果xpnew存在且不在障碍物内，将该点添加至随机扩展树中；否则退回Step 1，重新随机选取节点xprand。

Step 4判断新增的节点xpnew是否是目标节点xpgoal，如果是则求解成功，结束算法；否则重新进行Step 1。

在此迭代过程中，扩展随机树共有Tk个节点，新增节点xpnew的求解可由式(7)～式(9)求出：

xpnew=xpnear+

(7)

ypnew=ypnear+

(8)

zpnew=zpnear+

(9)

在扩展随机树的扩展过程中，prand为其随机生成的局部目标点。区别于其构造方式的不同，随机扩展树的形状亦会随之改变。笔者为提高扩展随机树的搜索效率，改进了prand的构造方式，引入了随机函数与参数pgoal-Possibility相结合共同生成局部目标点的方式。人工设定参数pgoal-Possibility表示了算法选取目标点pgoal为prand的可能性，如果pgoal-Possibility的值大于算法产生的随机数时自动选取pgoal作为局部目标点prand，否则随机生成局部目标点。该构造方式能够有效引导快速扩展随机树向着目标点pgoal方向进行生长，提高生长速度，优化算法的搜索效率。

RRT算法的扩展流程类似树枝的生长过程，原理明确构造简单，通过相同的算法不断随机采样新的状态节点，反复迭代递增生成扩展随机树。在引入参数pgoal-Possibility对扩展阶段进行优化后，扩展随机树的生长方向更具一致性，逆向查询出的路径更加平滑。

根据笔者的实际需求，改进的快速扩展随机树算法用于为移动机器人在路径中搜索临时目标点。因此适度增大扩展随机树的扩展步长γ，增大步长可以降低移动机器人调整位置姿态的频率，提高搜索效率，降低运动的时间，且移动机器人在进行实时路径规划时利用人工势场法可对障碍物进行有效的躲避，有效避免了增大步长后产生的与障碍物碰撞几率增加的问题，因此在APF-RRT融合算法的基础上增大扩展步长γ可有效改善路径的平顺性。

3 APF-RRT融合算法

3.1 融合算法的必要性

路径规划算法可以根据规划出的路径分为完备的路径规划算法和概率完备的路径规划算法。第一类算法在进行路径规划时如果起始点与目标点之间有路径规划的解存在，那么就一定可以计算并得出该解。此类算法为完备的路径规划算法，其优势为对路径是否可得问题的答案是肯定的，但随之亦会存在算法计算量大、算法结构复杂的问题，在环境信息较为复杂的情况下适用性很低。第二类算法如基于采样的路径规划算法，运行速度较快且其得到的路径规划解的集合概率完备，在高维空间下依旧适用；其缺点是此类算法可能会出现无法求出解的情况，且其生成路径的代价相较于第一类算法太高。

人工势场法在解决移动机器人路径规划问题时由于缺乏全局信息，在复杂环境中经常陷入局部最小值点，无法完成路径规划；快速扩展随机树算法作为一种概率完备的路径规划算法，在环境信息已知下的静态路径规划能力十分突出，但缺乏面对动态环境下实时避障的能力。笔者根据此两种算法的优缺点进行融合，在移动机器人使用人工势场法进行动态路径规划之前，使用优化的快速扩展随机树算法对静态已知环境中障碍物的分布情况提前进行预搜索；设置每个新状态节点为数个临时子目标点，对之后移动机器人使用人工势场法进行动态路径规划进行路径干涉与引导；通过优化的快速扩展随机树算法解决了人工势场法的局部最小值问题，并使得移动机器人在动态环境中亦具有很强的避障性能。

3.2 APF-RRT融合算法设计

在已知环境信息的静态地图上，先行使用RRT算法在先验地图上规划出一条可行的路径。该路径的起点和终点亦为移动机器人路径规划的起点和终点。再选取此条路径上的每一个新状态节点xpnew作为临时目标点，当移动机器人沿该条路径行驶时，使用人工势场法把初始路径上的每一个xpnew依次作为目标点；当移动机器人抵达第一个点后随即切换第二个点为目标点，依次类推直至抵达最终的目标点。APF-RRT算法流程如图4。

图4 APF-RRT算法流程Fig. 4 APF-RRT algorithm flow chart

APF-RRT算法具体步骤如下：

1)获取当前移动机器人初始位置xpstart，并检测该点是否处于障碍物内。

2)在空间中随机选取xprand作为临时目标点，判断人工设定参数pgoal-Possibility是否大于算法产生的随机数，是则选取最终目标点作为临时目标点，否则继续随机选取。

3)RRT算法规划完成后，选取路径上每一个xpnew依次作为移动机器人使用人工势场法进行路径规划时的临时目标点，引导移动机器人在该路径上行驶。

4)计算移动机器人与各障碍物间的欧几里得距离，求解障碍物对移动机器人产生的斥力与临时目标点产生的吸引力，得到斥力势能与引力势能之和。

5)计算障碍物与移动机器人间的向量与角度，并进行角度弧度转换，依次在各虚拟目标点间进行避障。

6)判断移动机器人是否抵达最终目标点。

4 仿真验证

笔者主要针对移动机器人在动态环境下的路径规划进行研究。为验证APF-RRT融合算法的必要性以及适用性，使用MATLAB平台进行仿真验证。移动机器人从起始点出发，成功到达目标点且过程中未与障碍物及地图边界发生碰撞，说明移动机器人避障成功。单独对传统的人工势场法进行仿真验证，与APF-RRT融合算法进行仿真对比。移动机器人运动控制参数如表1，仿真结果如图5～图8。

图5 人工势场法仿真示意Fig. 5 Schematic diagram of artificial potentialfield algorithm simulation

表1 移动机器人运动控制参数Table 1 Parameter of moblie robot motion control

在障碍物环境中设置L型障碍物、多个黑色静态障碍物与紫色动态障碍物。为测试移动机器人使用APF-RRT算法进行避障时不会陷入局部最小值点，并在路径规划过程中能够躲避动态障碍物，能够应对较为复杂的障碍物环境，在验证中加入道路约束。仿真结果显示，在10 m宽(y)、50 m长(x)的障碍物环境下，该算法能成功生成动态避障路径，而且能够保证移动机器人在低俗环境下的安全行进。在仿真验证进行的同时笔者将对移动机器人进行碰撞检测，如果移动机器人撞上地图边界或预先设置的障碍物，仿真过程将停止并表示路径规划失败。

图5表明，使用传统人工势场法的移动机器人在L型障碍物前、数个点状静态障碍物和一个动态障碍物附近陷入局部最小值区域且陷入震荡工况，移动机器人无法逃离该区域，路径规划失败。

图6 快速扩展随机树扩展过程Fig. 6 Expansion process of rapidly exploring random tree

图7的快速扩展随机树算法成功在静态障碍物地图上实现扩展随机树生长，并成功从最终目标点逆向迭代搜索出一条合理的路径。在该路径上存在的数个临时目标点引导下，移动机器人顺利地利用人工势场法规避掉移动障碍物，并最终到达目标点，路径规划成功。

图7 快速扩展随机树的路径查询Fig. 7 Path query for rapidly exploring random tree

图8 APF-RRT算法的路径规划Fig. 8 Path planning of APF-RRT algorithm

仿真结果表明，与快速扩展随机树算法融合之后，在利用该算法预先获得了部分的全局地图信息的情况下，成功解决了人工势场法中移动机器人易陷入局部极小值点的问题，在预规划路径上存在的数个临时目标点可以引导移动机器人进行路径规划。

5 结 语

在动态障碍物地图中，单一的路径规划算法难以满足复杂的环境情况，目前提出的路径规划算法或多或少均存在各自的优缺点。笔者提出的利用人工势场法与快速扩展随机树相融合的算法结合了两种算法的优点并互补了缺点，能够在动态环境中进行稳定的路径规划，生成清晰合理的避障路径，同时具有很高的适用性，概率完备，路径平顺性较好，能够确保移动机器人不与障碍物之间发生碰撞且有效减少了算法的计算量。仿真结果表明，笔者所研究的路径规划方法，在动态障碍物环境下能够进行有效的避障，同时具有较好的平顺性。在后续的研究中笔者将继续提高路径规划的舒适性、安全性。