结合改进角点检测的优化核相关滤波方法
2021-09-26景庆阳
景庆阳,李 波
辽宁工业大学 电子与信息工程学院,辽宁 锦州121001
作为计算机视觉的重要组成部分,目标跟踪集图像处理、模式识别及机器学习等于一身,在军事谋划、医疗诊治,乃至日常生活等领域发挥着越来越重要的作用[1]。近年来,相关滤波类的方法因其速度优势逐渐成为研究热点[2],将目标跟踪技术推向新的高度,得到广泛认可与应用。
该研究起步于国外,Bolm提出最小平方误差和输出(Minimum Output Sum of Squared Error,MOSSE)算法,应用快速傅里叶变换(Fast Fourier Transform,FFT)实现对目标的快速跟踪,至此Bolm成为将相关滤波器引入到目标跟踪的第一人[3]。基于MOSSE算法,Henriques等提出基于核循环结构的检测跟踪(Circulant Structure of tracking-by-detection with Kernel,CSK)算法,运用循环结构的密度采样方法,通过正则化最小二乘分类器来判别目标[4]。为更好地实现目标跟踪,将CSK的灰度特征用方向梯度直方图(Histogram of Oriented Gradient,HOG)特征代替[5],提出了具有多通道特征的KCF算法[6]。国内学者在KCF算法原有基础上层层递进,文献[7]引入了粒子滤波模型。尽管这种方法优于标准滤波算法[8],但依然无法完好地应对复杂多变的跟踪场景。文献[9]阐述了提升KCF算法速度的判别式相关滤波器在精确度方面未能达到理想效果。针对目标在不断运动的过程中难免出现尺度不确定等问题[10],为使目标中心位置估计值更为准确,本文针对分块KCF算法进行优化。
角点涵盖了图像重要的结构信息[11],是平面图像亮度发生剧烈变化的点或边缘曲线的曲率局部极大值点,是图像稳定的稀疏特征,应用于图像处理等诸多领域[12]。角点检测分为基于灰度强度检测和基于边缘轮廓检测[13]。本文主要研究前者,该方法通过图像局部灰度值变化的情况进而检测角点[14]。Morave首先发现不同区域灰度变化的模式存在明显差异:同质区域无论是何种方向,灰度变化都较小,但在边缘处仅有垂直于边缘脊方向时灰度的变化较大,角点处则为在多个方向拥有较大的灰度变化[15]。为对图像局部的灰度变化进行多尺度多方向的刻画,小波变换的运用将获取的结构信息完整地嵌入Harris框架中,便于实现角点检测[16]。为在提取图像灰度变化信息的同时减少运算量,Gabor小波应用于角点检测算法中[17],其性能有进一步的提升。由于Harris检测算子在光照变化等问题上有一定的不变性[18],可用Harris角点代替用广义霍夫算法提取的边缘点,从而实现目标位置的预测。
综上,本文的研究创新性在以下方面得以体现:
(1)采用Harris角点代替广义霍夫的边缘点,减小了因光照变化边缘点提取不完整而导致的误差。此外,数量适宜的角点还抑制了冗余边缘点导致的速度陡降问题。引入自适应阈值法,削弱噪声对角点提取过程的影响。
(2)当目标尺度发生较大变化时,KCF算法易丢失跟踪目标。本文将目标分块并利用子块间相对位置关系找到目标的中心点,用以提升KCF算法的准确度。
(3)当目标存在遮挡时,KCF算法的学习率无法随实际检测场景发生相应的变化。本文引入了学习率参数对其自适应更新,以降低学习率从而减少模型更新的误差。
(4)当目标快速运动时,KCF算法因结果易偏移而导致跟踪偏差。本文用交并比(Intersection Over Union,IOU)与匈牙利算法将多目标一一对应,取出相应的中心点坐标,再用Harris改进的广义霍夫算法得出的目标位置校正优化KCF算法的结果,抑制跟踪框的漂移现象,防止结果偏移的蔓延,提高目标跟踪的普适性与可靠性。
1 改进的角点检测算法
1.1 Harris角点检测
角点检测算法的核心思想:用一个固定窗口在图像上滑动,比较滑动前与滑动后窗口中像素灰度值的变化程度。若任意方向滑动,都发生较大的灰度变化,则窗口中存在角点。由于标准的角点检测有噪声等情况的干扰[19],Harris角点检测算法应运而生。当窗口的偏移量为[j,q]时,计算灰度变化值[20],将特征点和非特征点分离,滑动前后窗口中的灰度变化为:
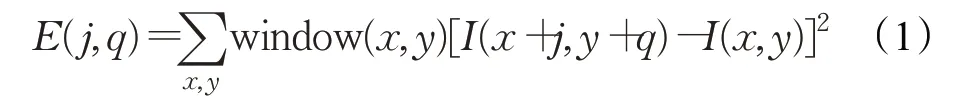
其中,I为图像的灰度,window(x,y)是高斯窗函数。由泰勒公式可知:

其中,Ix和Iy分别为x,y方向的偏导数,反映每个像素点图像灰度变化方向。可将式(1)写成矩阵形式:

角点响应函数R可判断像素点是否为角点:

其中,ε取[0.04,0.06],determinant(M)=λ1×λ2,trM=λ1+λ2,determinant(M)为矩阵M的行列式,trM为矩阵M的迹,λ1和λ2为矩阵M的特征值。由此可知,角点的判断只与特征值有关[21]。根据特征值大小,像素点可按照图1方式划分。

图1 角点判定方法Fig.1 Method of judging corner point
1.2 自适应阈值法
通常,只有给出合理的阈值才能提取出准确的角点[22]。若阈值选取过大,像素点的灰度值变化较大时,该点才能成为角点,从而易导致应有角点的丢失;若阈值选取过小,即使灰度值变化较小,该像素点亦可能成为角点,导致出现大量的伪角点。同时,某一特定阈值未必在各种图像中都能得到理想效果,普适性较差。只有找到每一图像的最佳阈值,Harris角点检测算法才能得到理想的角点。由于目前人为改变阈值的效率较低,故本文用自适应阈值来改进Harris角点检测算法。
通过观察并记录大量图像的R值找出每一图像的Rmax,其分布情况如图2所示,经分析得出:Rmax=u×108,其中u>0。定义Harris角点检测阈值T=k×Rmax,经大量实验可得:当0
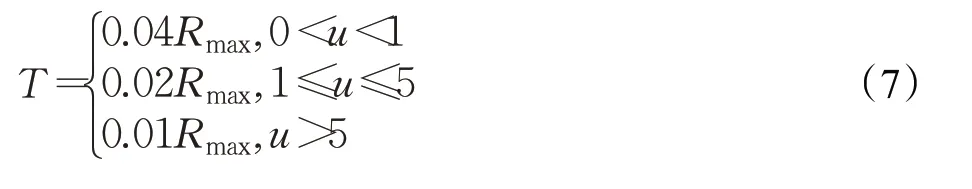
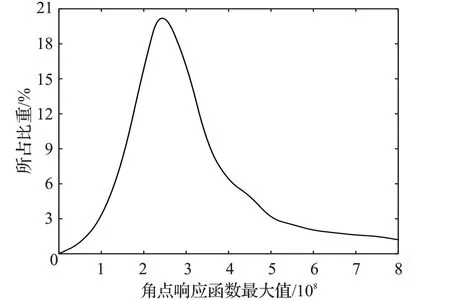
图2 最大值分布情况Fig.2 Distribution of maximum value
1.3 广义霍夫边缘点提取
目标边缘是特征突变的分水岭,包含着丰富的信息且不确定性较强。当目标形状不规则且无固定表达式时,广义霍夫算法可通过提取边缘点、生成特征向量来描绘目标形状,即找出相应的转换矩阵并确定参数,使目标边缘轮廓与其在场景中出现的位置匹配并构建参考点与边缘点间的位置关系,最终确定目标中心位置。
对于实际检测场景来说,边缘点较为冗余,易导致后续R-table表及累加器建立时间较长、实时性较差。由于实时性是评价算法能否应用于实际的重要前提,故本文用改进的Harris角点代替广义霍夫边缘点满足准确性与实时性的双重要求,该方法能根据图像的情况,自适应计算阈值并找到目标角点。
此外,边缘轮廓的描绘是广义霍夫算法的步骤之一。当目标检测场景发生光照变化或存在噪声时,截取的帧图像中像素点发生不同程度的变化,目标边缘与背景的区分度也随之变化,对边缘点的提取造成一定干扰,导致目标中心位置偏差。Harris角点的替换可大幅降低在光照及噪声变化条件下边缘点不完整提取或重复提取对目标中心位置的影响。结合自适应阈值描绘真实目标的形态学与动力学特性,弱化孤立噪声点与干扰点的影响,增强目标边缘点以平滑目标边缘轮廓,再现目标真实形状,免去繁琐的手动校调阈值工作。
2 优化KCF算法
2.1 标准KCF算法
KCF算法运用核化判别分类器[23],跟踪过程即为训练目标检测器的过程,用目标检测器来检测下一帧预测位置是否是目标中心位置,然后用新的检测结果来更新训练集,进而更新目标检测器。训练目标检测器时用循环移位操作构造更多的样本[24]。该训练过程是一脊回归过程,设训练样本集为(xp,yp),训练目的就是找到一个线性回归函数:f(z)=wTz,使误差函数Y最小。

其中,ξ可控制系统结构的复杂性,w为列向量,表示权重系数,通过最小二乘法可求解。将上述误差函数写成矩阵形式为:
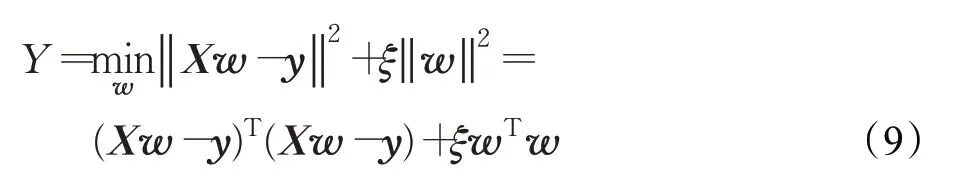
其中,X=[x1,x2,…,xn]T,y为列向量,每一元素对应一样本标签,F为离散傅里叶变换矩阵,FH为其复共轭转置矩阵。于是,可求得:

由于目标大多为非线性,引入核函数在将低维空间的x和y由φ(⋅)函数映射到高维核空间得到φ(x)和φ(y),高维数据的点积转换为低维空间核函数的运算。

这时权重向量w可表示为:
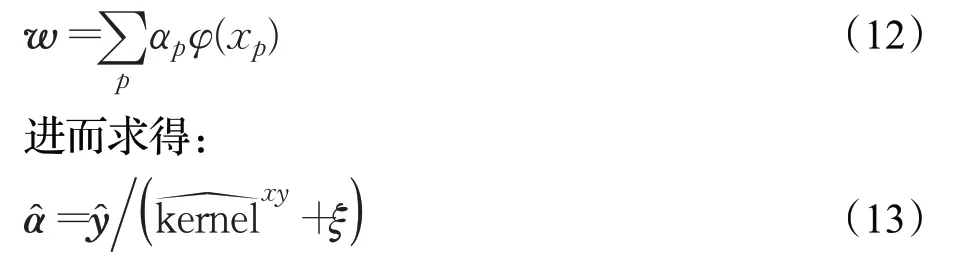
其中,符号“∧”表示向量FFT变换,kernel表示核输出:kernelxy=kernel(x,y)=φT(x)φ(y)。将求w的过程转化为求α,可降低计算的复杂度,使算法高效的进行。此时,样本的响应为:

其中,F-1表示傅里叶逆变换,f(z)中最大值对应的位置即为目标所在的位置。
2.2 目标分块
当跟踪过程中目标尺度发生变化时[25],KCF算法因模板框的尺寸固定而无法精准描述目标[26],导致跟踪结果精确度的降低。若第t+1帧目标尺度大于第t帧,此时KCF算法因模板框过小而导致跟踪结果不完整;若第t+1帧目标尺度小于第t帧,则因模板框过大易混入其他目标,使目标中心位置存在明显偏差。
本文针对以上不足做出相应改进:将目标按照外观特性分块,对每一目标子块进行单独跟踪,根据各子块间位置的约束关系进而得到目标整体的中心位置。虽然采用该方法子块的模板框尺寸也固定,但子块间的相对位置会随着目标大小的变化而变化。若目标变小,各子块间距离也变小而使子块重叠;若目标变大,各子块间距离也随之变大。因此,该方法可提高KCF算法的鲁棒性,解决由尺度变化而导致的准确度下降问题。
分块的方式及数量与目标实际的尺寸、被遮挡的位置及面积大小等因素息息相关。若子块数量过多,不但会增加计算量、影响算法的实时性,而且每一子块的覆盖面积过小、所含特征信息较少,易导致跟踪受到干扰使跟踪框漂移;子块数量过少,由于确定目标整体的中心位置存在偶然性,风险性较大,易引起算法跟踪性能的下降。经大量实验统计,当子块跟踪框大小为目标尺寸的1/4~1/6时,跟踪得到的中心位置与实际位置最为接近。此外,目标子块间应存在一定的区分性,若相似度过高,追踪器易被引导至相似的目标子块。
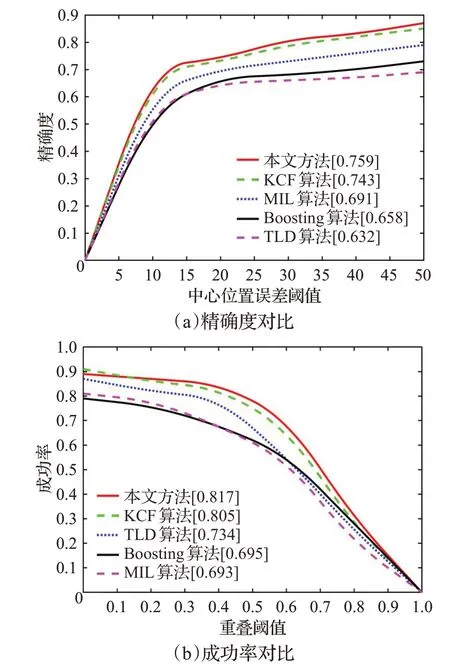
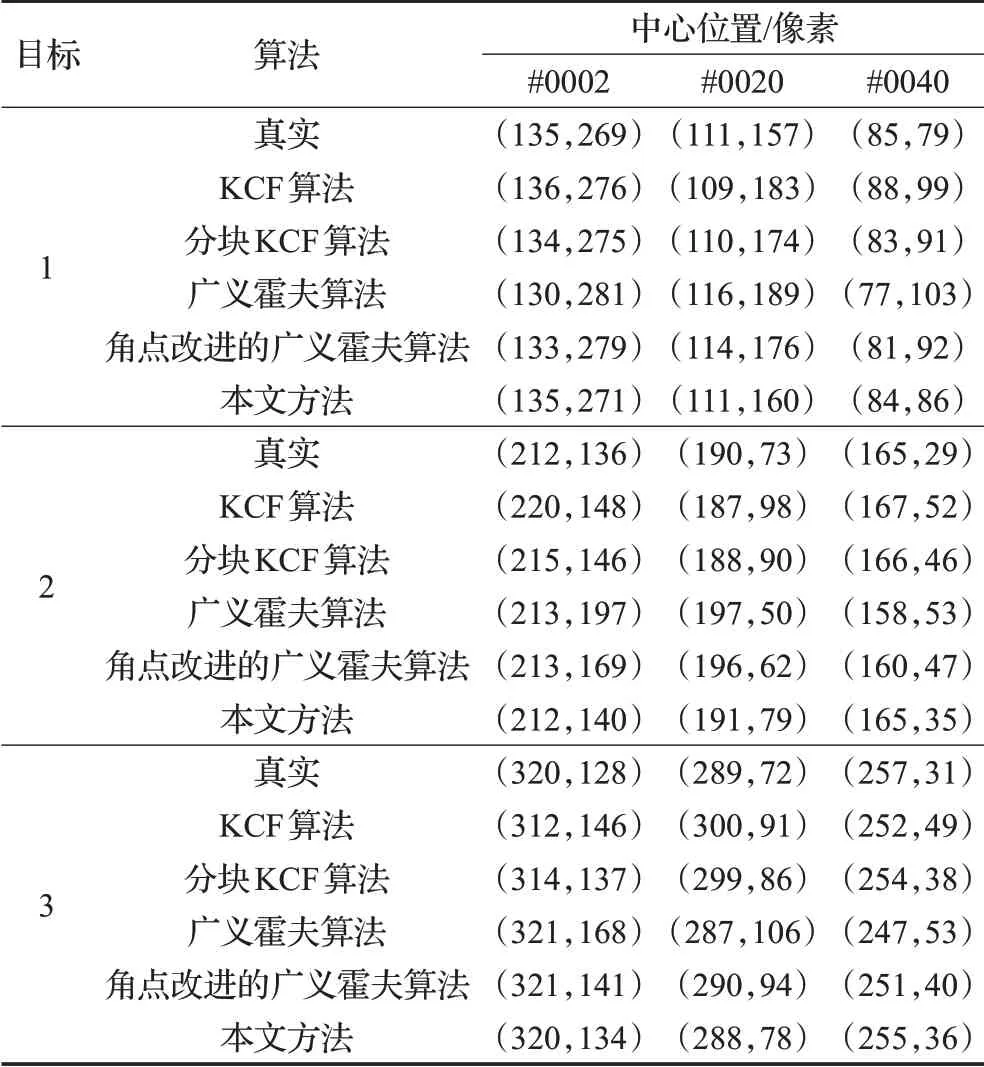
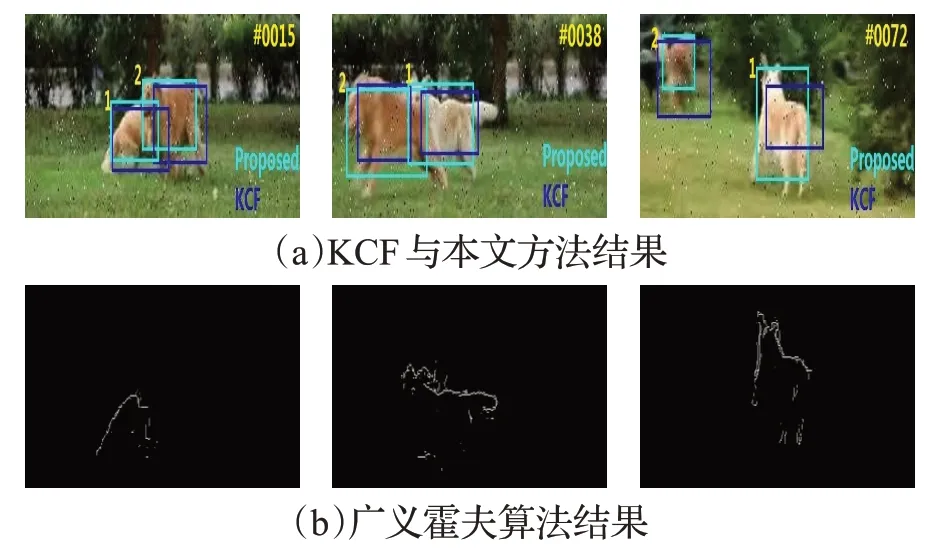
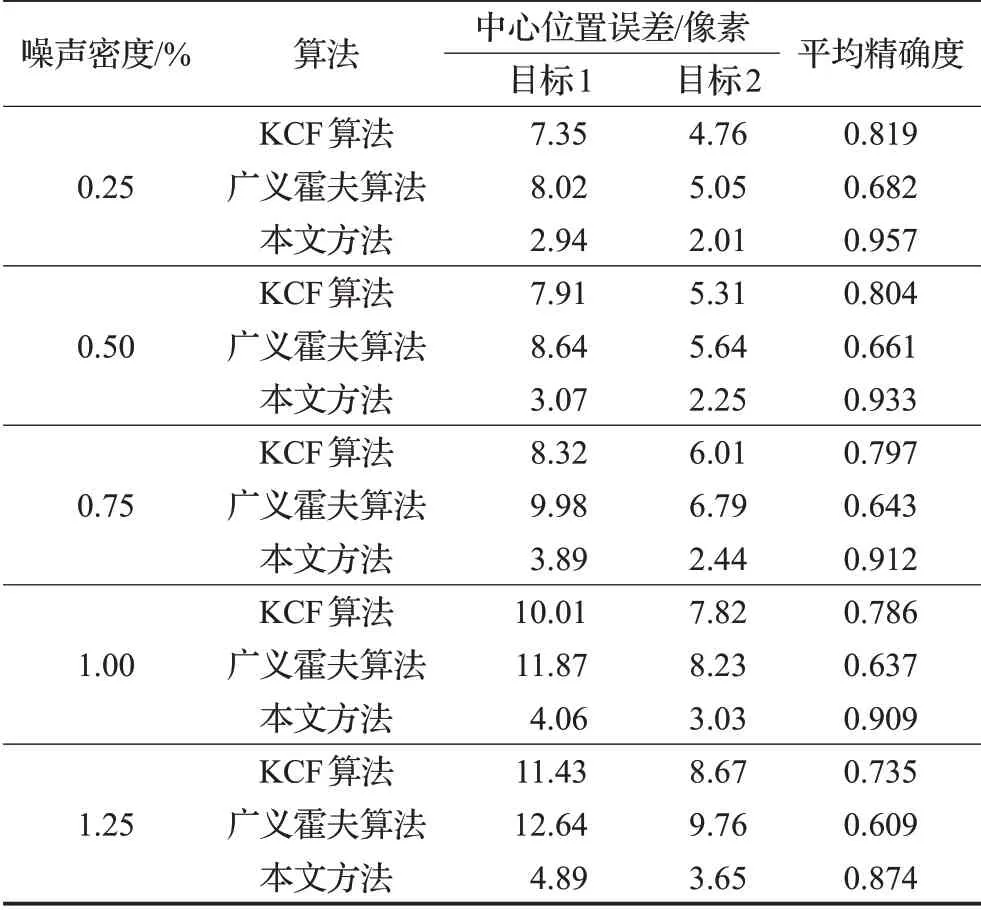
具体分块方式如下:首先计算目标纵横比,据此对目标进行分块处理。当目标的纵横比较阈值T1大时,将目标水平等分;当目标的纵横比较阈值T2小时,将目标竖直等分;当T2<目标纵横比 将目标分成均匀的m个子块后,找出每一滑动窗口与目标子块间特征向量相似度的最大值,该最大值对应的目标子块构成候选块。 峰值旁瓣比(Peak Sidelobe Ratio,PSR)可用来检测跟踪结果的置信度[27]。PSR值越大,响应图的相关峰就越尖锐,当前帧和前一帧的匹配程度就越高。PSR值越低,目标子块的遮挡情况就越严重[28]。本文剔除PSR值较低的子块对模型更新,具体如下: 其中,ψi为第i个子块的权重。 当目标存在遮挡时,降低学习率可减少模型更新的误差。但KCF算法中该参数无法随周围场景自适应变化,目标模型只在当前帧更新,导致跟踪结果不理想。对此,本文采用自适应更新学习率参数的方法,通过系数θ的引入降低学习率,解决目标被遮挡时跟踪结果不准确的问题,其更新方式如下: 用Harris角点建立R-table表来获取目标位置,具体步骤如下: (1)确定参考点。参考点为前一帧的跟踪点,若为首帧,则参考点为最初跟踪点。 (2)计算角点梯度角。获取目标Harris角点并计算每个角点当前帧的梯度角φs与其对应的行索引s,建立如表1所示R-table表。其中,φs为梯度角,a为参考点,r为Harris角点与参考点的相对矢量,B为角点集合,Δφ的选取与R-table表的行数和梯度角的范围有关。 表1 R-table表Table 1 R-table table (3)计算参考点坐标。当下一帧来临时,找到Harris角点的坐标并计算其梯度角,对应到R-table表中的相应行,求出与每个角点相对应参考点的坐标。计算累加器Acc,最大值对应的坐标为该帧跟踪点即参考点坐标。 (4)重复步骤(1)~(3),直到最后一帧为止。 在第t帧KCF跟踪器追踪到a͂个目标得到a͂个预测框。在第t+1帧追踪到c͂个目标得到c͂个真实框,构建一个大小为c͂×a͂的IOU矩阵,求法如公式(23)所示: 其中,∂1,∂2为目标框,Area为目标框的面积。 每一元素都表示两个目标框的重叠率。鉴于后续算法的需求该矩阵需为一方阵,若该矩阵行数与列数不相同需要用零补齐。采用匈牙利算法对该矩阵求最优解,找到第t帧与第t+1帧每个目标间的最优关联。由于目标框之间重叠部分越大越优与匈牙利标准算法中越小越优具有一定的冲突,因此先对矩阵中的每一元素取反,再运用匈牙利算法进行计算,可得KCF算法对应目标的序号,步骤如下: (1)对矩阵的每一行减去该行元素的最小值。 (2)对矩阵的每一列减去该列元素的最小值。 (3)在所用行数或列数最少的同时覆盖所有的零元素。若所用行列数总和小于该矩阵的大小,则继续步骤(4);若所用行列数总和等于该矩阵的大小,则此时即为最佳匹配,匈牙利算法终止。 (4)找到矩阵中没被覆盖的最小元素,在所有没被覆盖元素的基础上减去该值,在所有被覆盖两次元素的基础上加上该值,返回步骤(3)。 将用改进的Harris角点检测算法与用优化的KCF算法得到的目标位置进行相互校正:设在某一时刻最终得到的1号目标位置O的坐标为(x,y),经改进的Harris角点检测算法与改进的KCF算法得到的n组1号目标坐标分别为(x1,y1),(x2,y2),…,(xn,yn)。且与O点距离分别为e1,e2,…,en,如图3所示。 图3 目标位置示意图Fig.3 Schematic diagram of target position 然后,取出用两种算法得到的2号目标在不同采样时刻的位置,并用上诉方法计算其最终位置,依次类推。最后,结合各个目标的中心位置与其用广义霍夫算法描绘出的轮廓再次进行跟踪,以阻止快速运动时目标框偏移现象的发生。 本次实验采用Windows7 64bit PC操作系统,在主频为1.50 GHz,4 GB内存的配置环境下实现。其中,车的采集场景帧宽为1 280像素,帧高为720像素,速率为28帧/s。为准确分析并验证结合改进角点检测的优化核相关滤波方法的性能,采用MATLAB将多样例学习(Multiple Instance Learning,MIL)算法,跟踪学习检测(Tracking Learning Detection,TLD)算法,Boosting与KCF算法进行比较,具体参数设置如下:阈值T1=1.4,T2=0.6,学习率η=0.025,调节系数μ=0.85,面积因子ζ=0.3,遮挡阈值λc=0.8。这里,分块KCF算法的分块数量及方式随检测场景与目标纵横比的不同而变化。 精确度可用来衡量被跟踪目标的位置是否准确,中心位置误差(Center Location Error,CLE)的大小体现了结果精确的程度。在帧图像中,CLE为跟踪得到的目标中心坐标与真实位置之间的欧氏距离: 若CLE大于所设精确度阈值,则当前帧的跟踪结果不准确;若CLE小于该阈值,则当前帧的跟踪结果较为准确,且CLE值越小结果就越为精确。通常,精确度图横轴是CLE阈值,纵轴是CLE值小于该阈值的帧数占总帧数的比值(即精确度),由此可得随着阈值的变化精确度的波动情况。 成功率是衡量跟踪结果准确与否的另一标准,通过边界框重叠率(Overlap Rate,OR)来体现。OR为跟踪得到的目标框区域与真实标注目标框的重叠的程度: 其中,Ut为第t帧经跟踪获得的目标框的区域为该帧标注的目标框的区域。 若OR大于所设成功率阈值,则当前帧对目标的跟踪较为成功;若OR小于该阈值,则当前帧跟踪存在失误。通常,成功率图横轴为OR阈值,纵轴为OR值大于该阈值的帧数占总帧数的比值(成功率),由此可得随着阈值的变化成功率的浮动情况。OTB数据集中的视频序列有11种属性,代表了视觉跟踪的不同挑战场景,现用一遍过评测(One-Pass Evaluation,OPE)方式对比本文算法与多种当前流行算法的精确度、成功率等性能。 图4为在光照变化、尺度变化、遮挡、快速运动四种属性中,不同算法精确度和成功率曲线的整体性能对比。可以看出,当CLE的阈值取不同值时精确度的变化及当OR的阈值发生不同程度的变化时成功率的变化。当CLE的阈值为20,OR的阈值为0.5时,KCF算法的精确度和成功率分别为0.743和0.805,MIL为0.691和0.693,Boosting为0.658和0.695,TLD为0.632和0.734。本文方法由于角点的引入、目标的分块、学习率的降低及中心位置的校正,精确度和成功率分别为0.759和0.817。由此,本文方法无论是从精确度还是成功率方面来说较其他跟踪算法都有较为明显优势。 图4 精确度与成功率对比结果Fig.4 Comparison results of precision and success rate 为深入研究本文方法的优越性,分别在OTB数据集和实际检测场景中对跟踪算法性能进行测试。 图5为从OTB100中选取的具有代表性的帧图像与其用各种算法进行实验的结果。图5(a)是KCF与本文方法的跟踪结果,图5(b)是广义霍夫算法描绘出的目标轮廓。较其他算法而言,本文方法在兼有光照变化、尺度变化及遮挡属性的数据集中跟踪准确度较高。 图5 单目标跟踪结果Fig.5 Tracking results of single target 图6为采用各种跟踪算法图5中的目标在x和y方向的位置,可以看出无论是x方向还是y方向,代表本文方法的线离目标实际位置的线更近。由于光照变化广义霍夫算法只能描绘目标的部分形状,本文方法用Harris角点代替边缘点而使中心坐标更为精准。本文因学习率参数及分块方法的引入将手的遮挡及目标大小的变化对KCF算法的影响降为最低。由图可知,本文方法的跟踪结果比其他算法更接近目标真实位置。 图6 单目标中心位置对比Fig.6 Center position comparison of single target 图7为在实际检测场景中第2帧、第20帧与第40帧各种算法的跟踪结果。图7(a)是该场景中采用KCF算法与本文方法得出的结果,图7(b)是2号目标用广义霍夫算法检测的结果。当目标尺度发生变化时,KCF算法跟踪框的位置稍有偏差,但本文采用的分块方法能够根据目标尺度调整跟踪框的大小及位置。同时由于图中存在快速运动,广义霍夫算法不能完整地描绘出目标轮廓。由实验结果可知,本文方法由于多种算法的融合而不受快速运动的影响。 图7 多目标跟踪结果Fig.7 Tracking results of multiple targets 如表2所示,与广义霍夫算法相比,经Harris角点改进的广义霍夫算法离目标真实位置更近。本文所提方法在分别对KCF与广义霍夫算法改进的基础上,运用智能算法约束两者的位置关系,达到输入端相互校正目的,该方法比其他改进算法更接近真实位置。经分析发现,结合改进角点检测的优化核相关滤波方法在遮挡等尤为复杂的环境中能够突破常见跟踪算法有效性与可靠性之间的相互制约关系,获得较为理想的跟踪效果。 表2 多目标中心位置对比Table 2 Center position comparison of multiple targets 表3为各种跟踪算法在图7所示场景中的速度。由表可知,KCF算法速度最优为96.88帧/s,本文方法速度为32.95帧/s。该方法由于融合了广义霍夫、Harris角点检测等算法而不可避免地导致所需的时间较长,但能够大幅提升算法的跟踪精度。Boosting、TLD、MIL算法由于跟踪器存在不足而导致速度一般。广义霍夫算法由于提取的边缘点冗余,速度不到1帧/s,而用Harris角点代替边缘点后效果较为明显,速度有了大幅提升。 表3 多种算法速度对比Table 3 Speed comparison of multiple algorithms 由于实际场景中有时存在测量噪声,图8的信噪比(Signal to Noise Ratio,SNR)为51 dB,本文在该场景中进行鲁棒性测试,检测跟踪性能。由于天气原因,目标在快速运动过程中检测场景亦存在光照变化,广义霍夫算法轮廓的完整度有待提升。随着目标由远及近的变化,KCF算法的跟踪框不能随目标尺度变化而自适应调整。在第4帧图像中,目标2被目标3遮挡,此时KCF算法的跟踪偏差较为明显,但本文方法在复杂的环境中,能够有效跟踪目标,保证跟踪的精确度。 图8 鲁棒性测试Fig.8 Robustness test 由表4可知,用Harris角点代替边缘点,在光照变化、尺度变化、遮挡、快速运动四种属性中,都能够提升广义霍夫算法的精确度,其中光照变化条件下对精确度的提升最为明显。用自适应阈值法优化角点,可在原有基础上进一步提升算法精确度。因此,该阈值设置适用于大多数检测场景,普适性较强。 表4 广义霍夫算法改进前后精确度对比Table 4 Precision comparison of generalized Hough algorithm before and after improvement 不同信噪比下的平均精确度如图9所示。随着信噪比的上升,鲁棒性测试结果的平均精确度也越来越高。经统计,当信噪比为55 dB时,精确度仍高于0.95。实验表明,本文方法有较强的鲁棒性。 图9 不同信噪比下精确度对比Fig.9 Precision comparison under different SNR 图10给出了当椒盐噪声的密度为1%时多种算法的跟踪结果,图10(a)为用KCF算法与本文方法跟踪的结果,图10(b)进一步描绘出采用广义霍夫算法时目标1的轮廓。可以看出,在第15帧及38帧时,目标1被遮挡严重,广义霍夫算法无法准确描绘目标,KCF算法中心位置偏移。在第72帧处光照发生明显变化,对广义霍夫算法影响较大。即使没有出现遮挡,但所描绘的目标轮廓仍不完整。随着图中的目标与镜头间距离的改变,目标发生尺度变化,但KCF算法的跟踪框无法随目标的大小自适应调节。目标在快速运动的过程中亦发生形变,其余算法得到的中心位置均出现较明显误差。由本实验可知,当目标处于兼有遮挡、光照变化、尺度变化、快速运动等属性的复杂检测场景时,跟踪结果仍有较高的可靠性。 图10 椒盐噪声下的结果Fig.10 Results under salt-and-pepper noise 跟踪算法目标框的中心坐标与真实坐标间的欧式距离平均值为衡量跟踪准确程度的又一评估标准。表5所示中心位置的误差越小,跟踪算法的平均精确度越高。随着噪声密度的增加,各算法的跟踪误差呈上升趋势,但本文方法由于采用自适应阈值对Harris角点进行改进,弱化了孤立噪声点的干扰,增强了目标边缘轮廓。在所列不同强度噪声的干扰下,处理目标跟踪问题的能力始终优于其他算法。由实验数据可知,在图10所示复杂检测场景中,较KCF算法而言,广义霍夫算法在光照变化等多种属性的影响下,中心位置误差偏大,平均精确度偏低。 表5 不同强度噪声对算法性能的影响Table 5 Influence of noise with different intensity on algorithm performance 结合改进角点检测的优化核相关滤波方法,用自适应阈值准确找到帧图像的目标角点并有效去噪,同时降低光照变化条件下边缘点提取不完整对跟踪结果的影响。针对目标尺度变化引起的结果偏移问题,文中对目标进行分块处理、子块进行单独跟踪,根据各子块的中心坐标获得整体的位置。通过调整学习率参数降低KCF算法的学习率,解决目标存在遮挡时模型更新的误差问题。用已知的Harris角点建立R-table表得到目标位置,由匈牙利算法确定IOU数据间的最优关联,并综合两种方法得到的位置坐标与广义霍夫算法描绘的轮廓得到目标快速运动时的最优结果。实验结果表明,该方法可解决KCF算法在光照变化、尺度变化、遮挡、快速运动等属性中目标漂移与跟踪丢失的问题,大幅提升跟踪结果的精确度。 当非刚性物体遮挡较为严重时,本文方法跟踪速度稍显逊色。因此,如何在保证精确度和成功率的同时提高跟踪的实时性是接下来研究的重点。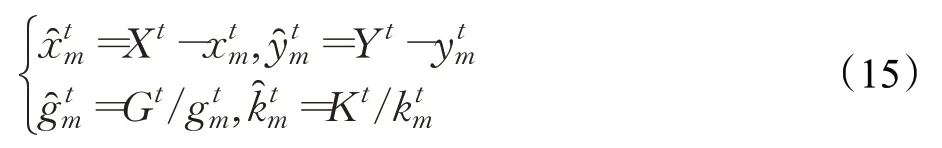

2.3 模型更新



3 信息融合方法

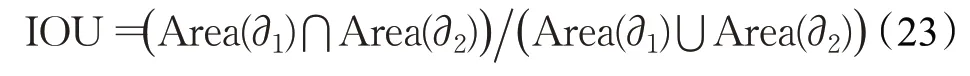


4 实验分析
4.1 实验环境
4.2 评估标准与定量分析


4.3 实验数据与仿真分析







5 结语
