摆锤摆臂受力分析

卢镇海，车江龙

（广东金马游乐股份有限公司，广东中山 528400）

0 引言

游乐设备在国外已有100 多年的发展历史，而中国的游乐设施起源于20 世纪80年代，起步相对较晚，各方面相对不完善［1］。游乐设备之所以吸引人，关键在于其能在确保安全的前提下，使乘客体验到惊险刺激，获得愉悦，享受快乐。正是由于游乐设备速度快、加速度大的特点，乘客体验惊险刺激的同时，也承担较大的风险。随着经济的发展，游乐设施越来越广泛地存在于人民的日常生活中，但游乐设备事故时有发生，这不但损害了国家的经济发展，更重要的是严重危害了人民的生命安全［2］。这是由于中国的游乐设施发展还不够充分，游乐设施安全仍然需要长久的积累与进步。

摆锤游艺机为由倾斜柱组成的支承架上装有支承轴，摆动吊臂绕支承轴来回摆动或旋转，吊臂下端装有座舱，座舱绕摆动吊臂旋转，或与吊臂固定的观览车类游乐设施［3－4］。刘海生等［5］对摆锤的三维设计做了研究；陈朝阳等［6］对摆锤的加速度做了分析；宋伟科等［7］对摆锤驱动头做了研究；薛真等［8］对含裂纹的摆锤减速器行星齿轮做了疲劳寿命分析；马栋联等［9］基于Solid Works对大摆锤机身做了有限元分析，但都没有对摆臂进行详细的理论计算。

本文在摆锤进行详细运动过程的分析下，对摆臂任一截面受力做了详细的理论计算［10－12］，可作为安全校核和新设计的参考。

1 受力分析

在驱动作用下，摆锤设备的摆臂绕支承轴旋转，来回摆动，摆臂下端装有座舱，一般座舱为圆盘结构，乘客沿圆周线均匀分布，有些摆锤设备的座舱可绕摆臂轴线旋转。摆臂运动过程中的荷载包括转盘对摆臂的荷载、摆臂重力荷载、摆臂运动产生的荷载。

摆臂整体做圆周运动，运动中产生荷载又包括离心力和加速旋转的荷载，分别计算这些荷载。从摆臂中取任一截面，对截取出来的一段摆臂运用刚体平面运动微分方程，计算得到运动过程中摆臂任一截面的荷载。

按由简到繁的规律，本文忽略了转盘自转带来的荷载，仅计算摆臂在平面内摆动时的情况，转盘自转的情况将在最后做出说明。任一时刻摆锤整体运动如图1 所示。

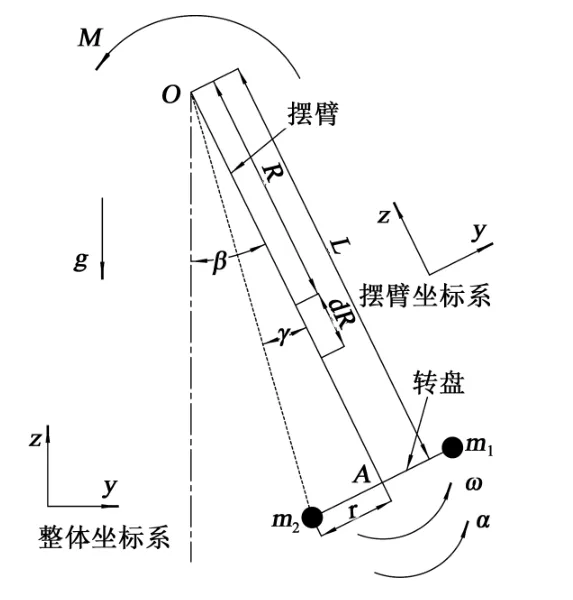
图1 摆锤整体运动

在重力和驱动力矩M作用下，摆锤的摆臂与转盘部分绕点O旋转。摆臂总长度为L，摆臂下端的圆形转盘半径为r，轻质转盘上有两个质量均为m的乘客m1和m2，m1、m2与点O的连线与摆臂轴线的夹角固定为γ。

对于转盘，由于粗略计算时，将转盘简化为质点计算转盘对摆臂的荷载，故本文重点关注角度γ带来的影响，简化转盘质量的影响，认为转盘质量为0，且让乘客只存在于转盘的两端，即转盘上只有图1 中位置的两位乘客m1和m2。

在摆臂与转盘运动过程中，由详细的动力学分析可知，当摆臂轴线与竖直方向夹角为β 时，运动部分的角速度为ω，角加速度为α。

整体坐标系与摆臂坐标系如图1 所示，整体坐标系z轴为竖直方向，摆臂坐标系z轴与摆臂轴线平行，随摆臂绕点O旋转，本文多采用摆臂坐标系。

1.1 整体动力学分析

摆臂与转盘是摆锤的运动部分，运动过程中运动部分所受的外力只有驱动力矩M和重力G，整体动力学分析如图2 所示。

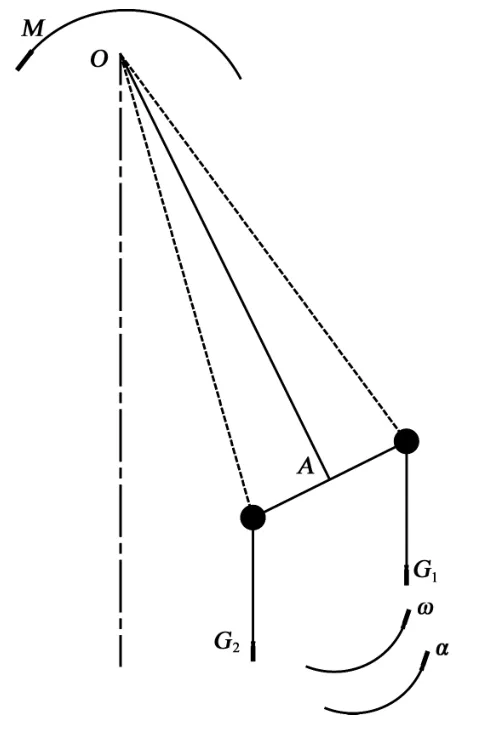
图2 转盘所受外力

设摆臂线密度为ρ，则摆臂部件对旋转中心点O的转动惯量为：

转盘上的两个乘客（质量均为m的质点）对旋转中心点O的转动惯量为：

转盘上的乘客对点A的转动惯量为：

对于摆臂与转盘整体列刚体绕定轴转动的微分方程有：

式中：MG，臂为摆臂的重力对点O的力矩；MG，盘为转盘的重力对点O的力矩。

当忽略γ角度，将转盘作为质点计算时，转盘的重力对点O的力矩为：

可以看出，忽略γ角度，转盘的重力对点O力矩计算出现一定的误差，计及γ角度时，计算复杂了很多。

1.2 转盘对摆臂的荷载

运动过程中，转盘部分在自身重力和摆臂对转盘的荷载作用下，绕点O旋转，建立转盘绕点O转动的动力学方程，求解摆臂对转盘的荷载，再取反力，得到转盘对摆臂的荷载。转盘的受力分析如图3 所示。

图3 转盘的受力分析

乘客的重力分为3 个分量，例如G1先沿径向与切向分解为G1τ和G1n，G1n再沿摆臂坐标系分解为G1n，y和G1n，z。其中G1τ与G2τ作为运动部件的动力之一，影响运动部分的加速度，此部分已在整体动力学分析中计算。G1n，y、G1n，z、G2n，y和G2n，z则作为结构荷载，经由转盘至摆臂，最终传递至基础。

乘客的离心力F1n和F2n由乘客的圆周运动产生，由于乘客运动的角速度和运动半径相同，故乘客的离心力大小相同，方向为分别沿两个乘客运动曲线的方向。容易判断，在摆臂坐标系下，两个乘客离心力在y向的分量互相平衡。

1.2.1 摆臂坐标系下转盘对摆臂的z向荷载

在摆臂坐标系下，转盘在z向无运动，故转盘所受的所有z向力平衡，设摆臂对转盘z向力为F′Az，转盘对摆臂z向力为FAz。

在摆臂坐标系下，乘客重力分量G1n，z和G2n，z的z向（摆臂轴线方向）分量为：

在摆臂坐标系下，两个乘客离心力的z向分量分别为：

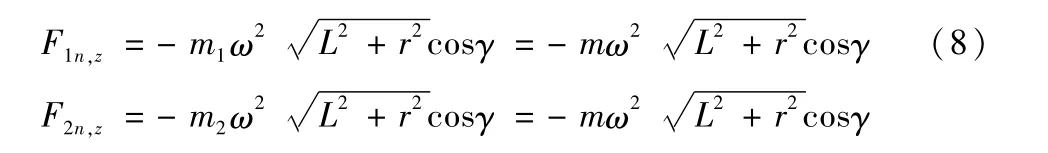
在摆臂坐标系下，建立转盘z向的平衡方程，求解转盘对摆臂对的z向力：

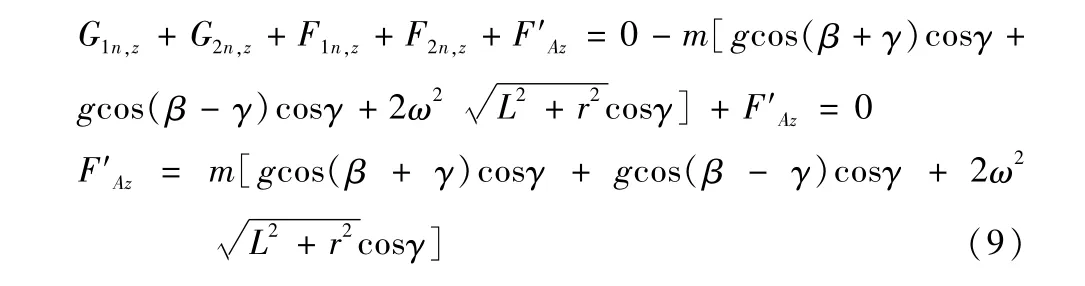
故转盘对摆臂的z向力为：

当忽略γ角度，将转盘作为质点计算时，乘客重力的z向（摆臂轴线方向）分量为：

乘客重力的z向（摆臂轴线方向）分量为：

转盘对摆臂的z向力为：

可以看出，当忽略γ 角度时，转盘对摆臂的z向力计算大为简化，但在乘客质量或转盘质量较大以及γ角度较大时，将引起较大的误差。在分析转盘对摆臂的y向力以及x向力矩时，也会因忽略γ角度而带来一定的误差，不再赘述。

1.2.2 摆臂坐标系下转盘对摆臂的y向荷载

在摆臂坐标系下，乘客重力分量G1n，y和G2n，y的y向分量为：

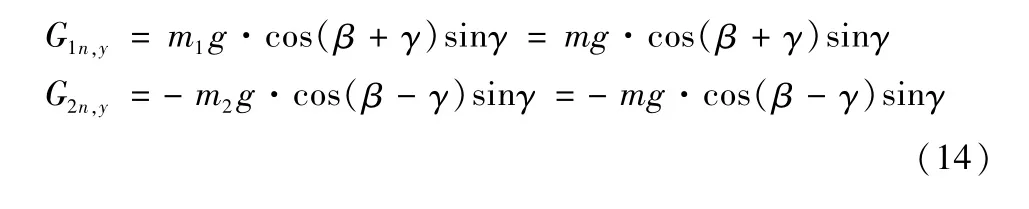
在摆臂坐标系下，乘客离心力的y向分量为：

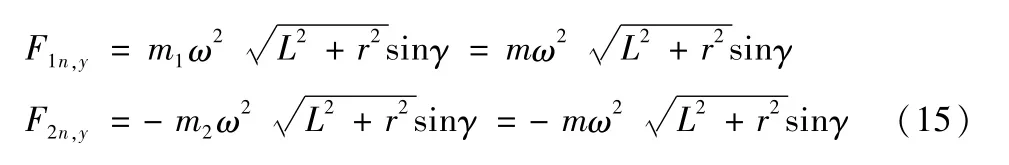
在摆臂坐标系下，设摆臂对转盘的y向力为F′Ay，由质心运动定理可得：

在摆臂坐标系下，转盘对摆臂的y向力为：

1.2.3 摆臂坐标系下转盘对摆臂的x向力矩荷载

在摆臂坐标系下，乘客重力分量G1n，z和G1n，z对转盘质心点A的x向力矩为：

在摆臂坐标系下，乘客离心力对转盘质心A的x向力矩为：

在摆臂坐标系下，设摆臂对转盘的x向力矩为M′Ax，由质点系对质心的动量矩定理可得：

在摆臂坐标系下，转盘对摆臂的x向力矩为：

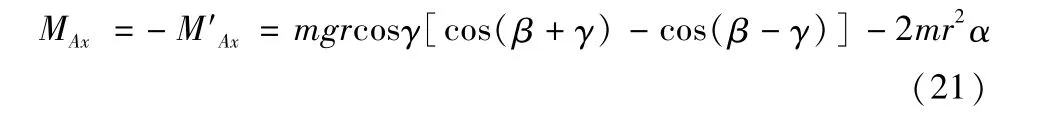
1.3 摆臂截面荷载

摆臂任一截面荷载的受力分析如图4 所示。

图4 摆臂任一截面荷载的受力分析

取距离点O为R的e段进行分析，其中A为转盘与摆臂连接面，B为摆臂任一截面，A截面的荷载即为转盘对摆臂的荷载，计算B截面的荷载即可得到摆臂截面荷载。由于摆臂不存在径向运动，故径向荷载互相平衡。

在摆臂坐标系下，转盘对摆臂的荷载为：

1.3.1 摆臂坐标系下摆臂截面的z向力

摆臂坐标系下，e段重力在z向的分量为：

摆臂坐标系下，e段离心力为：

摆臂坐标系下，摆臂在重力、离心力与截面荷载下z向的平衡方程为：

摆臂坐标系下，截面B的z向力为：

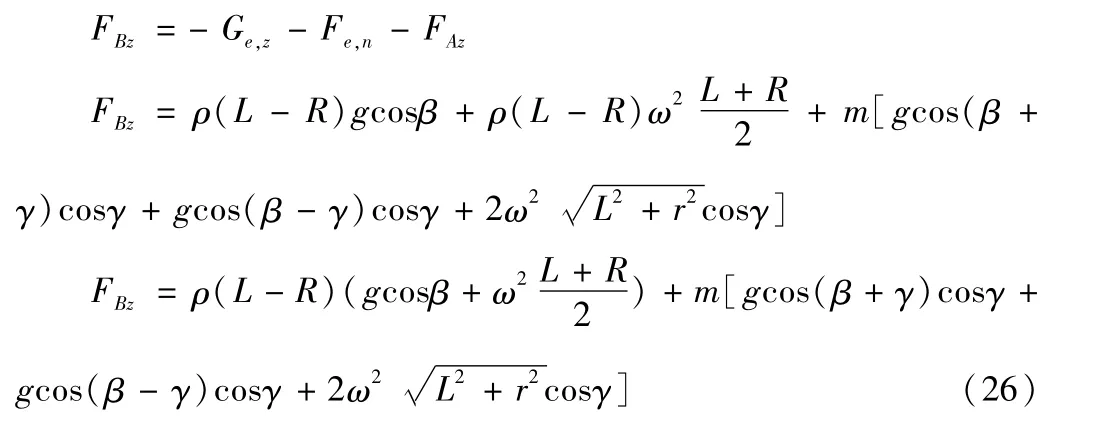
1.3.2 摆臂坐标系下摆臂截面的y向力

e段对其质心的转动惯量为：

摆臂坐标系下，e段重力在y向的分量为：

由质心运动定理可得，e段沿y向平动的运动方程为：

摆臂坐标系下，截面B的y向力为：

1.3.3 摆臂坐标系下摆臂截面的x向力矩

e段对其质心的转动惯量为：

由质点系对于质心的动量矩定理可得，e段绕质心转动的运动方程为：

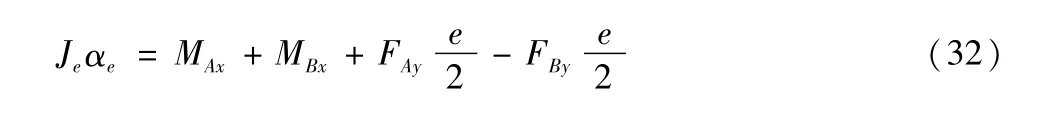
则摆臂截面的x向力矩为：

以上计算了摆臂做平面运动时，任一截面的荷载，先汇总如下：

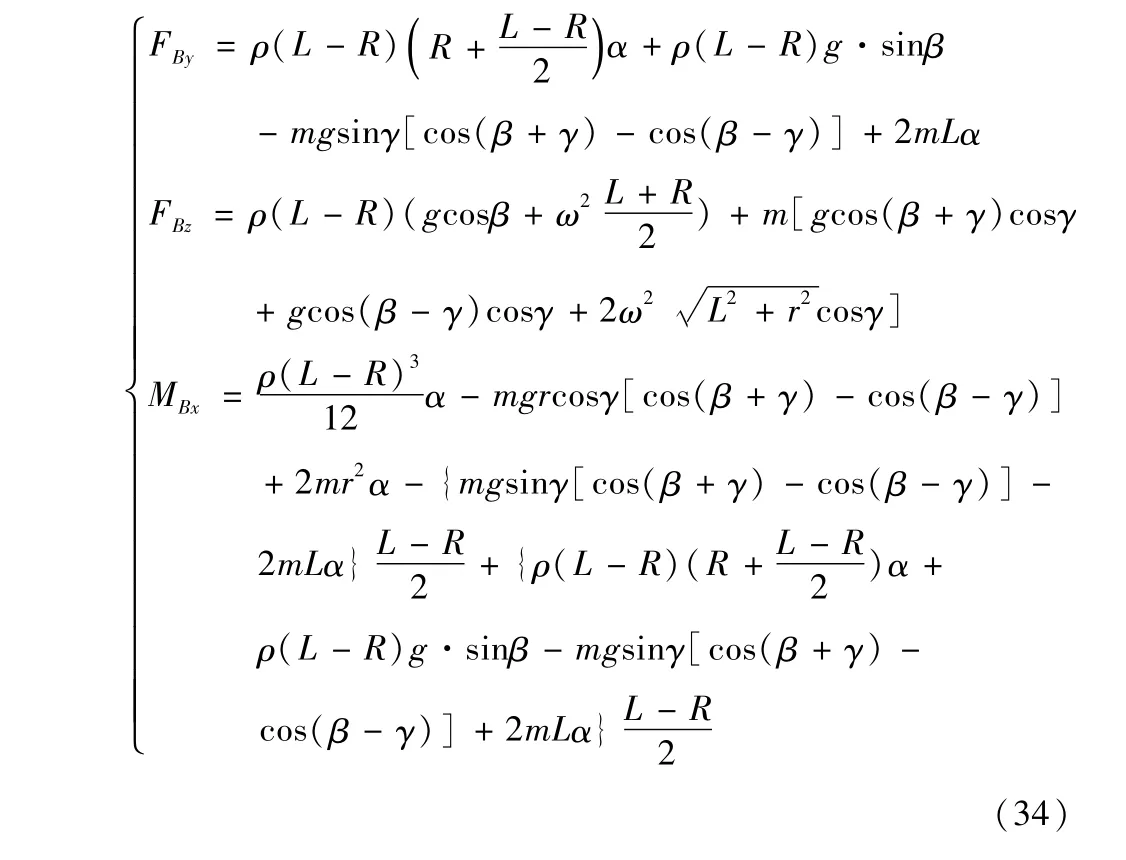
2 结束语

本文通过理论分析的方法推导出了摆锤设备摆臂任一截面荷载的详细计算公式，并给出了2 质点转盘模型对摆臂根部的荷载，此转盘模型虽然较为简化，但仍可说明转盘对摆臂荷载的所有要素。例如，以往计算转盘对摆臂荷载时，粗略地将转盘重力直接按摆臂径向与切向分解，而当γ较大时，将引起较大的误差。实际中转盘一般乘客较多，但仍可用本文的方法进行计算。当考虑主盘自转时，转盘对摆臂有科氏力作用，一般将满载转盘作为均质圆盘计算，所有的科氏力将合称为一个y向力矩，将此力矩添加到摆臂的计算方程中，即可得到满载情况下摆臂任一截面的荷载。当转盘乘客为偏载情况时，还应计算偏载导致的荷载，将此荷载添加到摆臂的计算方程中，即可得到偏载情况下摆臂任一截面的荷载。本文的计算结果可以为摆锤的摆臂设计提供更详细的计算参考，提高设计的安全性。