一种水平机器人动力学模型辨识方法

彭云春，曾 钰

（广州智能装备研究院有限公司， 广州 510530）

0 引言

在机器人的运动控制中，往往需考虑机器人的关节在工作作业时的电机扭矩范围，既要满足关节的伺服电机在最大扭矩范围内，又要满足超额定扭矩的占比在某个数值范围内，这就少不了对动力学模型的计算。传统的对于动力学模型的参数辨识，往往将动力学模型进行符号转换合并，化为最小参数矩阵来辨识连杆本体和摩擦相关的参数，此过程涉及变量相对多，过程也相对繁琐、复杂[1-3]。由于目前机械加工精度的逐渐提高，水平机器人Scara 本体的机械惯量参数，通常理论和实际相差甚小，同批次不同本体的差异，往往只是由于生产和安装工艺的差异，在摩擦/转子惯量相关的参数会有明显的区别。鉴于此，采取理论的机械惯量参数+摩擦/转子惯量系数的辨识来建立水平机器人Scara动力学模型，方法相对简单清晰、实现难度低、辨识流程短、可操作性强，可以满足轨迹规划中电机扭矩的估算。

1 动力学模型的建立

水平机器人Scara 主要有基座、大臂、小臂、丝杆4 个部分，其动力学模型分析的结构模型如图1所示。其中大臂、小臂的运动平面与重力方向垂直，由矢量叉积可推得第1、2轴运动中的电机出力与重力无关，丝杆包含上下运动（第3轴）和旋转运动（第4轴），上下运动方向同重力方向同线，旋转运动平面同重力方向平行，也可由矢量叉积得到第4轴运动中电机的出力与重力项无关。采用传统的拉格朗日方法建立的通用机器人的动力学模型[4-8]如下：

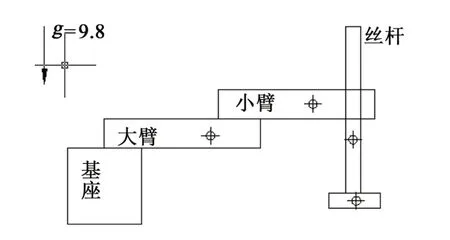
图1 Scara结构模型Fig.1 Scara structure model

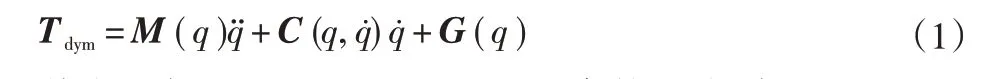
其中，每个连杆包含10 个惯性参数，分别是质量、质心 、 惯性张量， 可用惯性参数集表示为p＝[Ixx,Ixy,Ixz,Iyy,Iyz,Izz,Mx,My,Mz]。如机构为n连杆结构，则为10n个惯性参数，水平机器人为4连杆机构，按此方法为40个惯性参数。

根据水平机器人Scara 的结构特点， M (q) 为惯性矩阵；C (q,) 为科里奥利力和离心力；G(q)为重力项； Tfric为摩擦力项[9-10]； Tj为传动转子惯量项。考虑摩擦力项、转子惯量项，可获得水平机器人Scara 具体完整的动力学方程T（式5），其中每个连杆的摩擦力项Tfric关联2个参数[B,τf]，转子惯量项Tj关联1个参数[J]。

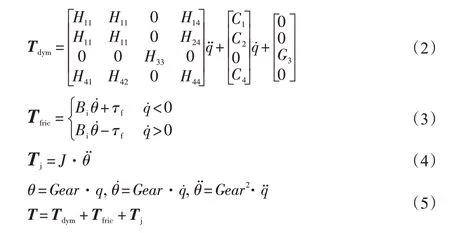
式中：θ为伺服电机旋转角度，与q存在减速比Gear对应关系，将Tfric和Tj两部分合并为Tfj如下：

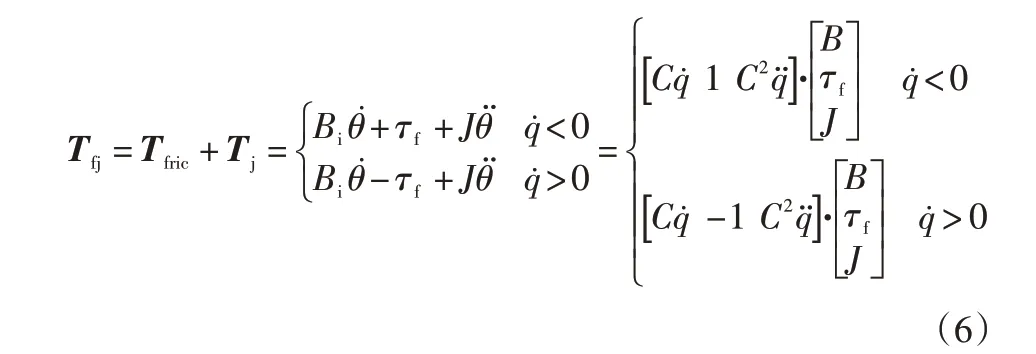
得到：

由式（7）可以看出，考虑到每个轴的摩擦力项和转子惯量项参数，动力学参数有40+3×4=52 个参数变量，而由于机构的运动因素，有些参数项是不会影响运动中电机出力的，是无法得到有效辨识的。因此，传统辨识过程的方法是先对这些参数项作简化处理，化简为最小惯量参数集后再来进行辨识。最小惯性参数集计算公式[8]为：

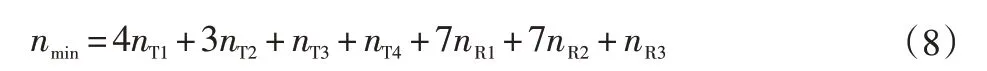
其中，水平机器人第1 轴为R3 型，第2 轴为R2 型，第3轴为T3型，第4轴为R2型，那么水平机器人可得到最小惯性参数为16 个。考虑到每个轴的摩擦力项和转子惯量项参数，动力学参数仍有16+3×4=28 个参数变量，辨识过程仍计算复杂，且多为矩阵计算，也容易造成矩阵奇异，影响辨识的正确性。

鉴于水平机器人本体的结构和制造工艺，其本体制造引入的机械惯量参数偏差很小，机械的理论惯量参数在本体设计时就已明确，而摩擦因数和减速机电机转子惯量在本体设计无法给出。基于此，可不作最小惯量参数化简，直接采用水平机器人本体理论惯性参数计算，只进行摩擦/转子惯量的参数辨识，从而有效把辨识参数减少到12个参数，便于控制应用。

2 摩擦/转子惯量的参数辨识

由式（7）得：

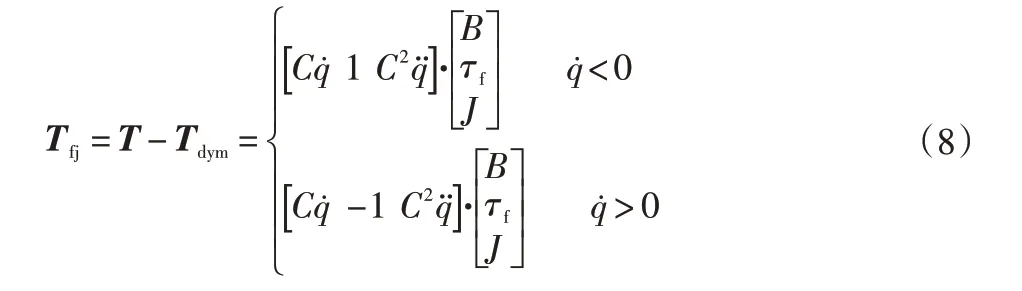
令：

则可得：

通过工业总线的方式，运行轨迹以1 ms 的周期采样伺服驱动对应编码器数据、实时电流数据，经滤波处理后，转换为对应关节角度q、关节速度、关节加速度、关节力矩T。将采集的若干组数据关节角度q、关节速度q、关节加速度，通过式（2）可计算得到Tdym，从而式（10）左边可得；通过将该组数据的关节速度、关节加速度代入式（9）中，可得到矩阵A；对矩阵A 按行进行关节轴1～4 分类，可计算得到各轴的摩擦/转子惯量参数。根据式（10），最终可得到如下矩阵等式：

依次采用最小二乘方法可求得各轴的摩擦/转子惯量参数[Bj,τf,Jj]数据。

3 实验验证

采用本公司自主研发的驱控一体控制器、水平机器人Scara 本体，本体的惯量参数通过Solidworks 获取。如图2～3所示的惯性张量（由输出坐标系决定）。

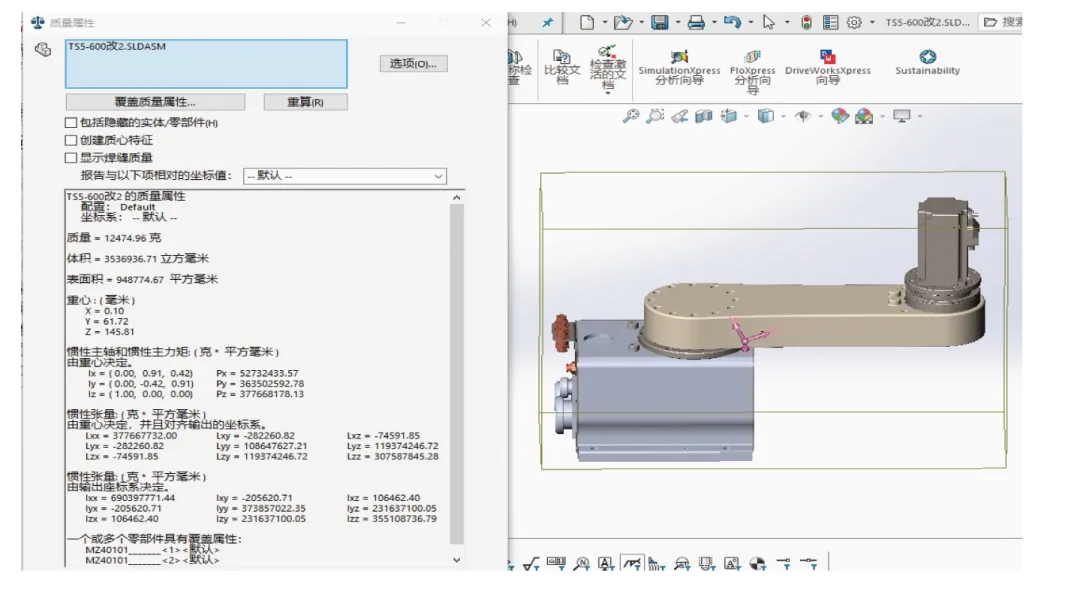
图2 Scara本体大臂惯量信息Fig.2 Inertia information of Scara main body arm

对轨迹运行的数据实时进行电机编码位置、电流进行1 ms采样存储，对位置、电流数据进行FFT 变换，进行频域分析，设计滤波器滤波后，其中位置、电流波形如图4～6 所示。对采样数据通过第2 节的摩擦/转子惯量的参数辨识处理，可分别求得第1～4 轴对应的[B,τf,J]，分别如表1 所示。根据辨识的参数，验证不同轨迹下的理论计算电机力矩和实际电机力矩的峰值对比，如图7所示。从图中可以看出，力矩曲线间会存在一些差异，这部分差异主要是由于本体惯量参数造成，但对于轨迹规划中电机扭矩的估算，该差异可近似忽略。

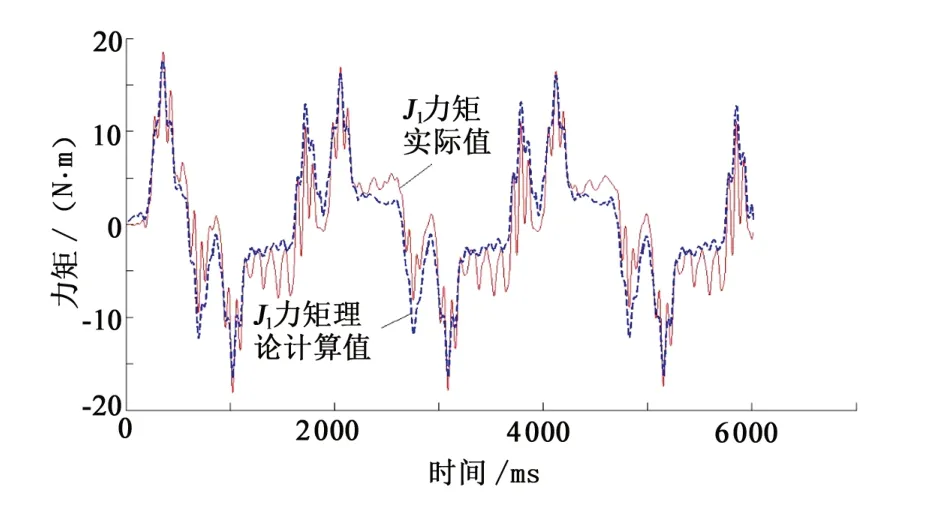
图7 第1轴的采样力矩和计算力矩Fig.7 Sampling torque and calculated torque of the first axis

表1 第1轴～第4轴辨识的摩擦/转子惯量系数[B, τf , J]Tab.1 Friction / rotor inertia coefficients identified for the first and fourth shafts [B, τf , J]

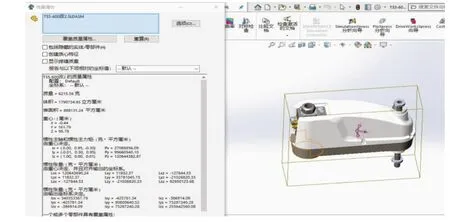
图3 Scara本体小臂惯量信息Fig.3 Inertia information of SCARA body small arm

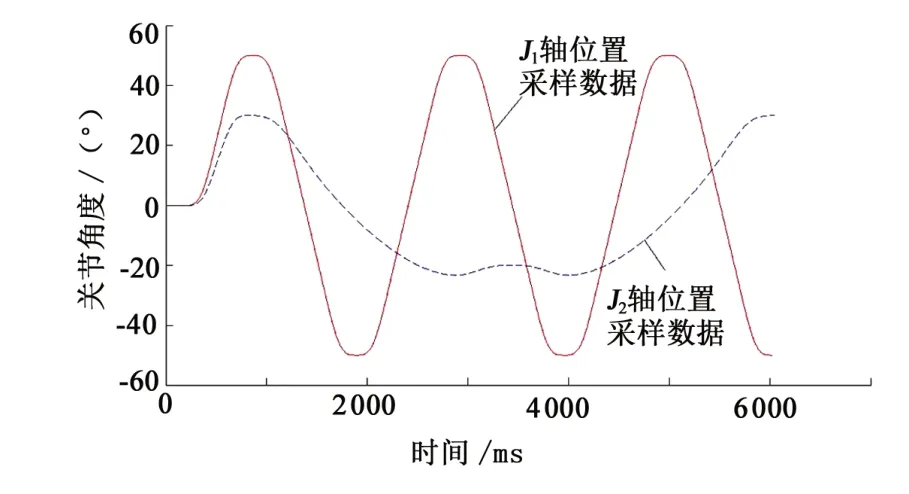
图4 J1轴、J2轴位置-采样数据Fig.4 Position of axis J1 and J2-sampling data

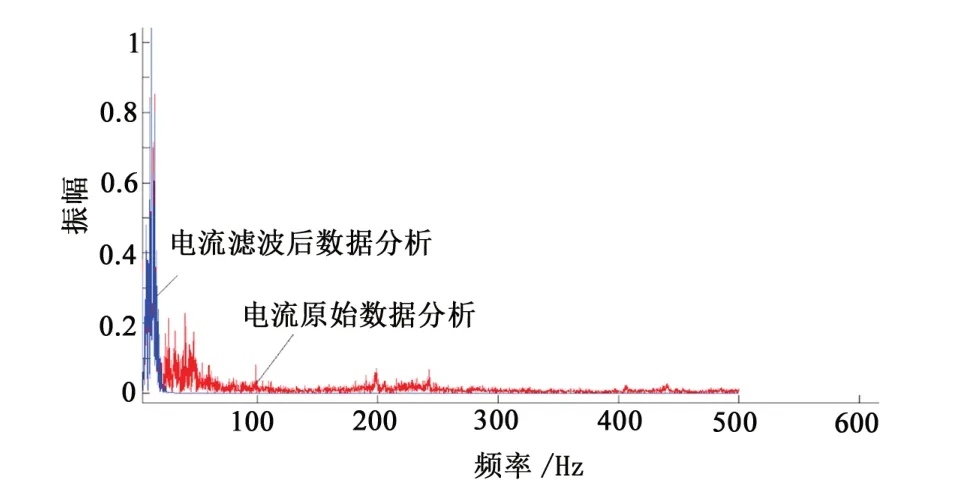
图5 J1轴电流数据原始/滤波后振幅谱Fig.5 Amplitude spectrum of original / filtered current data of J1 axis

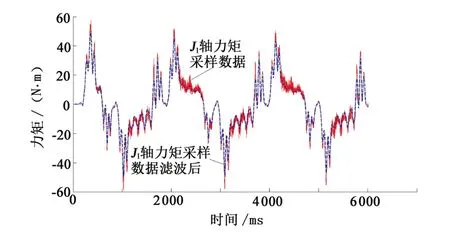
图6 J1轴力矩采样数据和滤波曲线Fig.6 Torque sampling data and filtering curve of J1 axis

4 结束语

在机器人控制系统中，应用动力学技术时，传统模型辨识关联过多的参数变量，易造成的数据采集处理步骤繁琐、计算量大，从而不便于在产品中应用。基于此，本文提出一种水平机器人动力学模型简化辨识的方法。该方法基于拉格朗日的动力学模型，通过采集本体轨迹和电流实时数据，用最小二乘法来辨识摩擦/转子惯量系数。从实验效果来看，采用该方法辨识的参数，理论计算的力矩同实际电流采样力矩轨迹曲线近似相同，误差较小，可满足轨迹规划中电机扭矩的估算要求。本文的方法相对简单清晰、实现难度低、辨识流程短、可操作性强，易于在产品中应用。