循环冲击下节理表面粗糙度对其法向刚度与形貌的影响
2021-09-26石竟成李建春李星何磊
石竟成,李建春,李星,何磊
(1.东南大学土木工程学院,未来地下空间研究院,江苏南京,211189;2.上海市政工程设计研究总院(集团)有限公司,上海,200092)
随着我国基础建设水平的不断提高,资源开发、交通运输、与国防建设等领域均有向地球深部发展的趋势。不同于浅表地层,深部地层主要由成因和完整程度不同的岩体构成。岩体是岩石材料和其结构面的总称。岩体结构面包括原生结构面、构造结构面和次生结构面,其中以构造结构面分布最广[1]。构造结构面是岩体在构造运动中形成的破裂面,根据成因和构造特点的不同,构造结构面分为层理、断层、劈理和节理,其中节理是分布最广的一种构造面。由于节理的存在,节理岩体表现出不均匀性、不连续性、各向异性和非线弹性的复杂性质[2]。因此,对于节理岩体力学特性的研究在岩石工程中具有重要意义。
目前,关于节理岩体在静态或拟静态荷载作用下的力学特征的研究已较为成熟。GOODMAN等[3]最早提出了法向刚度与切向刚度的概念。BANDIS 等[4]在前人的基础上通过大量的单轴压缩、循环加载和直接剪切试验建立了应力与节理闭合量之间的静态Bandis-Barton(B-B)模型。在动力学的研究范畴中,应力以应力波的形式作用在岩体上。应力波在传播过程中会在节理面上发生透射、反射和折射。在多次透反射后,应力波的波速、幅值和能量均会发生衰减[5]。根据节理和应力波的相互作用,ZHAO 等[6]在静态“B-B”模型的基础上提出了动态“B-B”模型。LI等[7−8]提出了一种时域递归法的分析方法(time domain recursive method),此方法可通过建立应力波在节理中的传播方程从而计算出应力波在节理处的传播情况。
节理表面的几何特征是影响节理岩体力学特征的关键因素。描绘节理表面几何特征的常用参数有节理粗糙度系数(JRC)[9],节理吻合度系数(JMC)[10]、节理表面形貌特征和节理厚度等。目前,有关岩石动力学的试验研究主要采用一维霍普金森压杆和三维霍普金森压杆试验技术[11]。刘婷婷等[12]采用一维分离式霍普金森压杆试验技术研究了节理接触面积对节理动态力学特征的影响,发现节理刚度随接触面积增加产生的规律性变化。CHEN等[13]采用改进霍普金森花岗岩杆建立了节理吻合度、节理厚度和节理聚合程度对节理动态力学特性影响的规律性曲线。LI等[14]将分离式霍普金森杆试验技术与3D打印技术相结合,深入研究了应力波通过不同几何特征的节理面时应力波幅值的衰减规律。为研究应力波作用于节理面时能量的衰减与耗散规律,LI 等[15]利用品质因子Qs衡量应力波的能量耗散,发现随着节理粗糙度系数JRC的增大,应力波通过节理面时耗散的能量也随之增大的规律。
目前,大多数对于节理岩体动力学特征的研究仅建立在一次冲击且节理试样未发生损伤破坏的前提下。然而,岩体在自然情况下受到的地震或爆破产生的应力波影响,其承受的动态荷载往往是多次或循环的[16]。当岩体受到此类荷载的影响时,大多会产生一定程度的损伤。谢和平等[17]在拟静态的条件下对岩石进行循环压缩试验,并建立了岩体单元在循环压缩荷载下的整体破坏准则。SHU 等[18]采用分离式霍普金森压杆试验技术研究了热处理后的花岗岩在循环冲击荷载作用下的能量衰减规律。而有关不同节理表面形貌特征的岩体在循环冲击荷载作用下的动态力学特征和破损规律还有待研究。为了开展定量的研究,本文作者采用浇筑成具有不同节理粗糙度的类岩石试样,即采用水泥−花岗岩颗粒混合浆液现浇试样模拟天然状态下的节理岩体,开展霍普金森压杆(split hopkinson pressure bar,SHPB)试验,研究循环冲击下节理的法向刚度以及应力波能量耗损规律与节理粗糙度之间的关系。另外,采用三维形貌扫描技术计算试样实际节理粗糙度系数,并对比循环冲击前后节理面的几何特征变化。
1 试样准备和试验技术
1.1 试样制备
试验采用水泥−花岗岩颗粒混合浆浇筑而成的类岩石试样模拟节理岩体,试样为长×宽×高为35 mm×35 mm×40 mm的长方体。浇筑试样时,利用3D打印技术制作的模具形成不同粗糙度的锯齿状节理。试样节理粗糙度系数采用YANG等[19]改进的Tse经验公式进行计算:

其中:

式中:CJR为试样节理粗糙度系数;L为节理宽度。
设计节理粗糙度系数分别为0(光滑),1.6,7.3,11.4,14.5,17.1和19.3 共7 种试样,每个试样分为完全吻合的2 部分,节理试样示意图如图1所示。
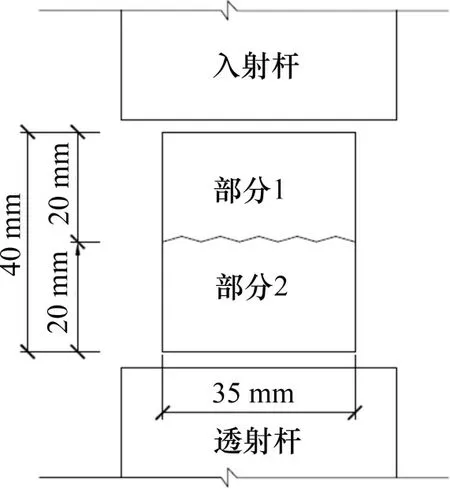
图1 水泥−花岗岩颗粒混合浆浇筑的节理试样示意图Fig.1 Specimens with artificial joints poured by cement−granite particle mixture
试样在浇筑过程中受众多因素影响,节理表面几何形貌的实际值与设计值往往存在差异。利用三维形貌扫描技术,得到试样的实际节理面轮廓线,再由式(1)可得试样的实际节理粗糙度系数,如表1所示。
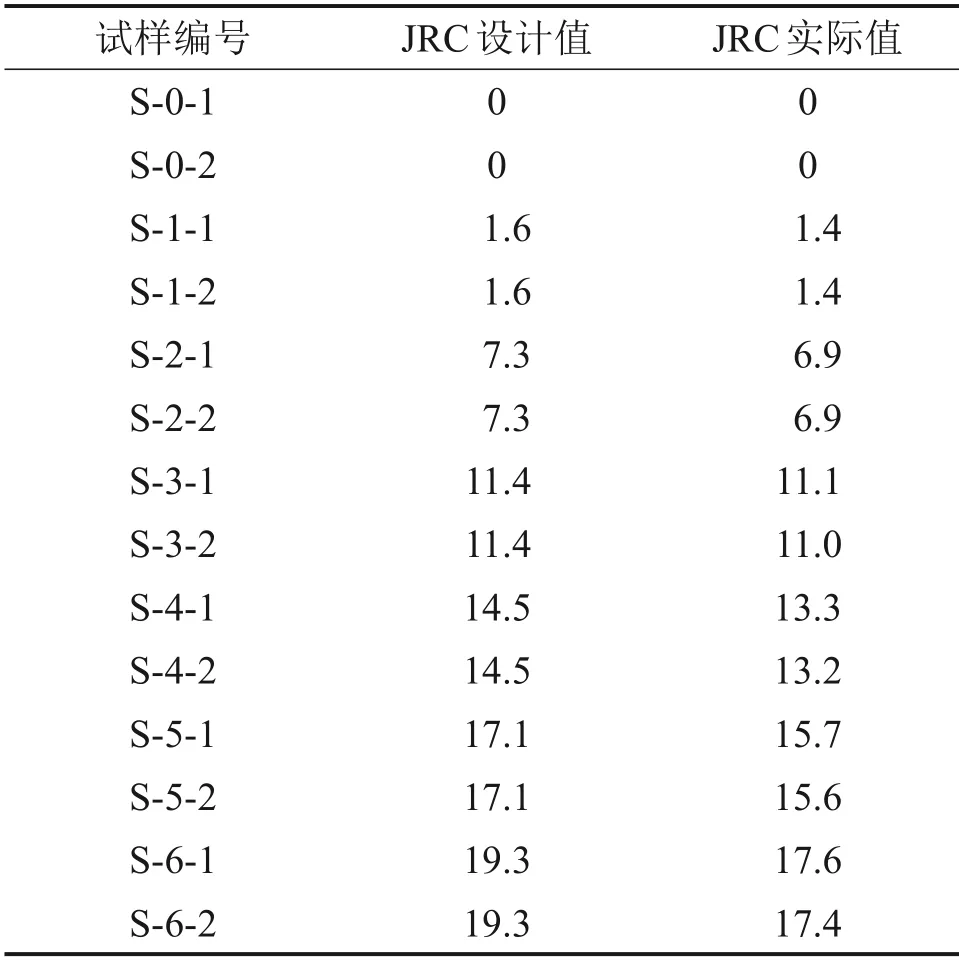
表1 试样节理粗糙度系数实际值Table 1 Actual JRC of samples
水泥−花岗岩颗粒混合浆中,水泥为52.2硅酸盐水泥,花岗岩颗粒粒径为0.5~1.0 mm。水泥、花岗岩颗粒、水质量比为1:0.5:0.3。为测定材料的静力学参数,浇筑3个标准圆柱体试样,试样底面直径为50 mm,长径比为2:1。3个圆柱体试样的平均静力学参数如下:28 d平均抗压强度为71 MPa,平均密度为2 270 kg/m3,平均弹性模量为22 GPa,平均泊松比约为0.3,纵波的平均波速为3 774 m/s。3组试样单轴压缩试验的应力−应变曲线见图2。可见:本试验采用的类岩石材料与天然岩体的静态力学参数接近,可用来模拟天然岩体的相关力学特征。
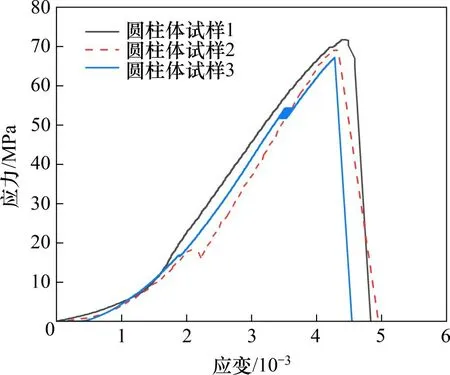
图2 单轴压缩试验应力−应变曲线Fig.2 Stress−strain curves of uniaxial compression test
1.2 SHPB试验
本试验采用东南大学−蒙纳士大学苏州联合研究生院的常规一维SHPB 试验装置。SHPB 系统主要包括加载设备、入射钢杆、透射钢杆、吸收钢杆、阻尼器和数据采集系统,其示意图如图3所示,其中,加载设备为摆锤,摆锤摆长为1.5 m,铜锤的截面直径为50 mm。摆锤在配合量角器使用时可产生小速度冲击波,且冲击速度较为稳定。
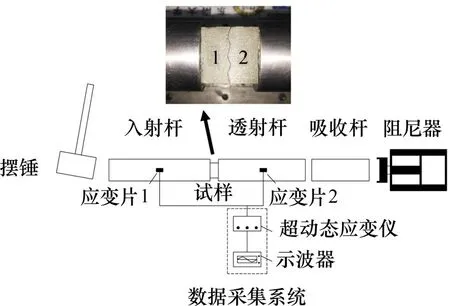
图3 SHPB系统示意图Fig.3 Sketch of SHPB system
试验系统的钢杆均为高强弹簧钢,其材料参数为:密度7 800 kg/m3,弹性模量210 GPa,纵波波速5 189 m/s。入射杆、透射杆与吸收杆截面直径均为50 mm,其长度分别为2.5,2.0和1.0 m。阻尼器位于透射杆的末端,起到限制吸收杆运动与吸收能量的作用。
数据采集设备为与惠斯通电桥配合使用的超动态应变仪与示波器。入射杆的应变片1粘贴于入射杆表面距离杆端1.25 m处;透射杆应变片2粘贴于透射杆表面距离杆端1 m 处,均由对称粘贴的2个应变片组成,应变片的桥路均采用双应变片半桥接法,桥路可将应变信号转化为电压信号,显示并储存在示波器上。
1.3 三维节理形貌扫描技术
采用3D System 公司生产的3D Capture扫描系统研究节理形貌,该系统由相机、支架、转台和校准板组成(图4),转台可自动旋转360°,并由相机拍摄不同角度的数字影像。数字影像经Geomagic Control软件计算并合成三维数字影像。

图4 3D Capture扫描系统实物图Fig.4 3D Capture scanning system
1.4 试验方法
试验采用摆锤加载的SHPB。为滤掉入射波中的高频波,减小波弥散造成的实验误差,同时保证试样中的应力−应变在试验中达到均匀,试验采用入射波整形技术。经反复尝试,将紫铜片作为整形器粘贴在入射杆杆端。试验前,先将试样进行三维节理形貌扫描,然后在试样两端及试样上下两部分之间涂抹少量黄油,使之紧密接触。试验时,为使得反复冲击后,仅节理面发生破损而非岩体完全破坏或粉碎,摆锤采用小角度反复冲击节理试样。经反复尝试,角度为25°(速度约为1.3 m/s)时,试验效果最为理想。每个试样均采用冲击速率为1.3 m/s 反复冲击若干次,直至试样表面出现贯通裂纹,记录冲击的入射波、透射波和反射波波形,并对冲击后的试样进行三维节理形貌扫描。
2 试验结果及分析
2.1 试验所测波形图
图5所示为相同冲击速度循环冲击下入射波和透射波的典型波形图。经整形片整形后的入射波上升沿持续时间约为500 μs,应力波在试样中的传播速度为2 800 m/s,波在试样中传播一次的时间为14.3 μs,入射波上升沿的持续时间足够其在试样中来回传播2~3次,故试验满足一维霍普金森杆应力−应变均匀性假定[20]。

图5 相同冲击速度循环冲击的典型波形图Fig.5 Typical waveform of cyclic impact at the same impact speed
由图5可看出:当应力波作用在类岩石试样上时,应力波的幅值发生明显衰减。结果表明:应力波幅值的衰减程度与类岩石试样的节理表面粗糙度及作用在试样上的循环冲击次数均有关。在冲击速率保持稳定的前提下,入射波的幅值大致相同,透射波的幅值随节理粗糙度系数的增大而减小。对于同一个试样,前几次冲击得到的透射波波形和幅值变化不大,而最后一次冲击时,试样产生贯通裂纹,且透射波幅值明显比前2~3次冲击的小。
2.2 试样的应力−节理闭合量关系分析
得到的结果均采用三波法[21]进行处理,最终得到试样所受的应力和应变。在试验中,由于冲击速率较小,可假设节理试样的主体部分在完全接触时仅发生线弹性变形。此时,节理闭合量可根据胡克定律,由式(2)计算:

式中:Δuj为节理闭合量;σ为试样所受的应力;ε为试样所受的应变;l0为试样总长;li为节理长度;Er为完整试样的弹性模量。
由于前三次冲击未对节理试样产生明显影响,为描述方便,将前三次冲击称为初次冲击,最后一次冲击称为最终冲击。试样S-0~S-6初次冲击和最终冲击的应力−节理闭合量曲线如图6所示。定义曲线顶点与原点连线的斜率为节理法向刚度kn。从图6可见:试样S-0~S-6 初次冲击的平均节理刚度分别为1 380,1 090,824,682,610,527和516 MPa/mm;最终冲击的节理刚度分别为954,899,652,548,510,457和434 MPa/mm,冲击至节理面破坏后,节理法向刚度减小约20%。图7所示为循环冲击下节理法向刚度与JRC 的关系曲线。从图7可以看出:当冲击速率一定时,节理粗糙度越大,节理刚度越小,且同一试样在出现贯通裂纹时的节理刚度明显小于试样未破损时的节理刚度。
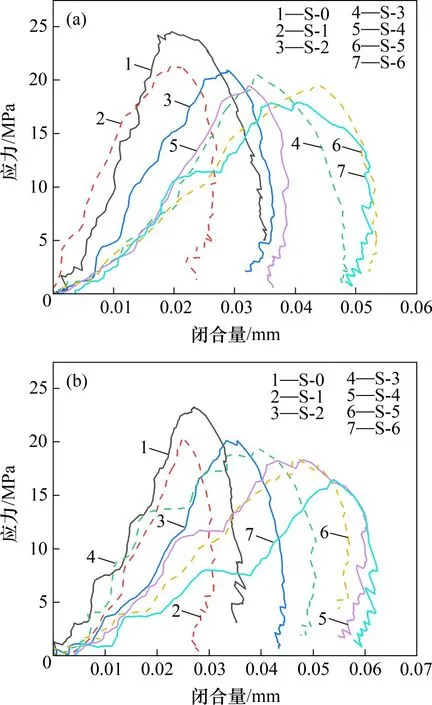
图6 节理试样冲击应力−节理闭合量曲线Fig.6 Stress−joint closure curve of samples

图7 节理法向刚度与JRC关系曲线Fig.7 Relationship between joint normal stiffness and JRC
2.3 循环冲击下的应力波能量耗损
在霍普金森杆试验中,当应力以应力波的形式作用于类岩石试样上时,应力波的能量会产生耗损。在干燥岩体中,应力波耗损的能量主要包括岩石部分的颗粒摩擦耗能和节理部分耗能[14],其中,节理部分耗损的能量又由节理面摩擦耗能和节理面损伤耗能组成。本文主要讨论由于节理面损伤而产生的应力波能量耗损。
钢杆系统的能量可分为入射能Wi(t)、反射能Wr(t)、透射能Wt(t)和变形能Ws(t)。由于每次试验所需时间较短,可认为钢杆系统不与外界发生能量交换。在系统内,当应力波穿过节理试样时,杆件对试样做的功记为U(t),且U(t)=Wi(t)−Wr(t)−Wt(t)。根据热力学第一定律,杆件做的功均转化为变形能Ws(t),故试样的变形能可由式(3)计算[14]:
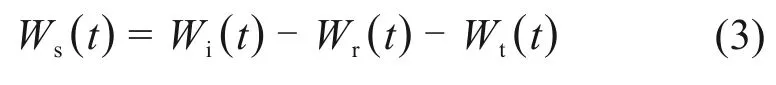
式中:
图8所示为完整试样和试样S-1 在冲击过程中的能量变化。从图8可见:入射能量、透射能量和反射能量均在冲击后从0 开始增大,直到最大值。变形能在起初试样发生变形时开始增大,这是由入射杆对试样做功引起的。当变形达到最大时,部分变形恢复,变形能开始减小,最终稳定。由于试样端部涂抹润滑黄油,故忽略节理面摩擦产生的能量耗损。最终试样的变形能并未恢复到0,其主要原因为:1)岩石部分由于颗粒摩擦而消耗了少量能量,记为Ws0(t0);2)节理部分由于节理面破损而产生了能量耗损,记为Wsj(t0)。其中,Ws0(t0)由完整试样冲击试验测得。本试验中测得Ws0(t0)为2 J,由于冲击速度稳定,每次冲击的入射能变化较小,因此可认为Ws0(t0)为固定值。本研究用变形能Wsj(t0)衡量每次冲击由于节理面损伤而消耗的能量,用衡量因节理面损伤而消耗的总能量,其中,t0为变形能达到终值时的时间,j为冲击次序,n为该试样的冲击至产生贯通裂纹所需的冲击总数。为消除入射波幅值和能量对损伤耗能的影响,由于每个类岩石试样破坏所需的冲击次数不同,采用损伤总耗能与入射能平均值的比值分析损伤总耗能与节理粗糙度系数JRC之间的关系。

图8 试样冲击过程中能量时程曲线Fig.8 Energy time history curves of samples in process of impact
图9所示为不同粗糙度的节理试样冲击至破损所需的总能量。在相同的冲击速率下,当试样的节理粗糙度从0(光滑)增加到17.6 时,由节理面破损而耗损的总能量分别为126.9,54.1,38.7,29.0,26.9,16.7和15.6 J,由节理面破损而耗损的能量比值分别为6.68,2.77,2.10,1.52,1.42,0.93和0.83。这是因为,随着节理粗糙度系数JRC 增加,节理表面形貌越来越复杂,节理表面出现应力集中的点也越来越多,节理刚度下降,在循环冲击的过程中,节理试样发生破坏的难度也随之下降。也就是说,节理粗糙度系数越大,节理试样破坏所需的总能量越小。
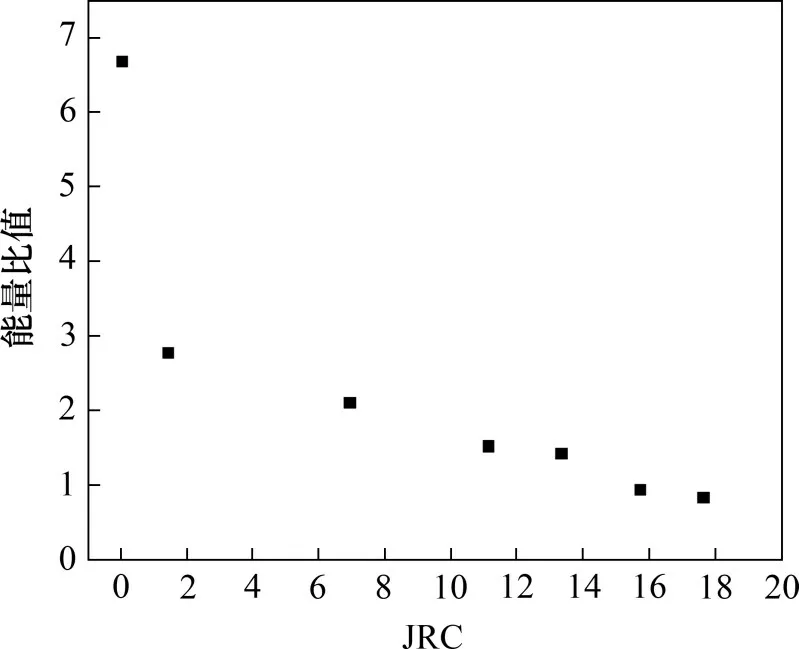
图9 节理粗糙度与能量比值Wsj(t0)/(t0)关系Fig.9 Relationship between JRC andWsj(t0)/(t0)
2.4 循环冲击对节理面几何形貌的影响
为了将循环冲击下节理试样的动态力学特征与节理表面形貌变化相结合,每次冲击后,均对节理试样进行三维节理形貌扫描,然后采用配套软件Geomagic Control对冲击前后的节理表面形貌进行比较。图10所示为试样S-1第3次冲击前后以及最后一次冲击前后的节理表面形貌的三维对比图,冲击前后节理形貌的高程差越大表示节理形貌变化越大。

图10 试样S-1冲击试验前后节理表面形貌对比Fig.10 Comparison of morphology of joint surface before and after impact test
表2所示为不同粗糙度的节理试样破坏所需的冲击次数及冲击前后节理面的最大高程差。由表2可见:试样S-1第:3次冲击前后节理表面最大高程差约为0.250 8 mm,最终冲击前后的最大高程差约为0.714 0 mm;试样S-2 第3 次冲击前后节理表面最大高程差约为0.328 6 mm,最终冲击前后的最大高程差约为0.882 8 mm。可知,在试样未破坏时,冲击前后节理表面最大高程差均不超过0.5 mm,即前几次冲击并未对节理面产生明显影响。随着冲击次数的增加,节理表面的损伤不断累积,在最后一次冲击时,节理面最大高程差明显增大,节理表面出现明显的裂纹,即该节理试样破坏。另外,节理试样破坏所需的冲击次数随节理粗糙度的增加而减少。这是因为,循环荷载的冲击速率保持稳定,每次冲击产生的入射能大致相同,冲击次数可在宏观上反映入射波的总能量。由于变形能与入射能的比值波动范围不大,因此,类岩石试样破坏所需的冲击次数与试样破坏所需的总能量保持正相关关系。从表2还可以看出:无论在试样破坏前还是破坏后,随着JRC 的增大,冲击前后节理表面高程差都有所增加。
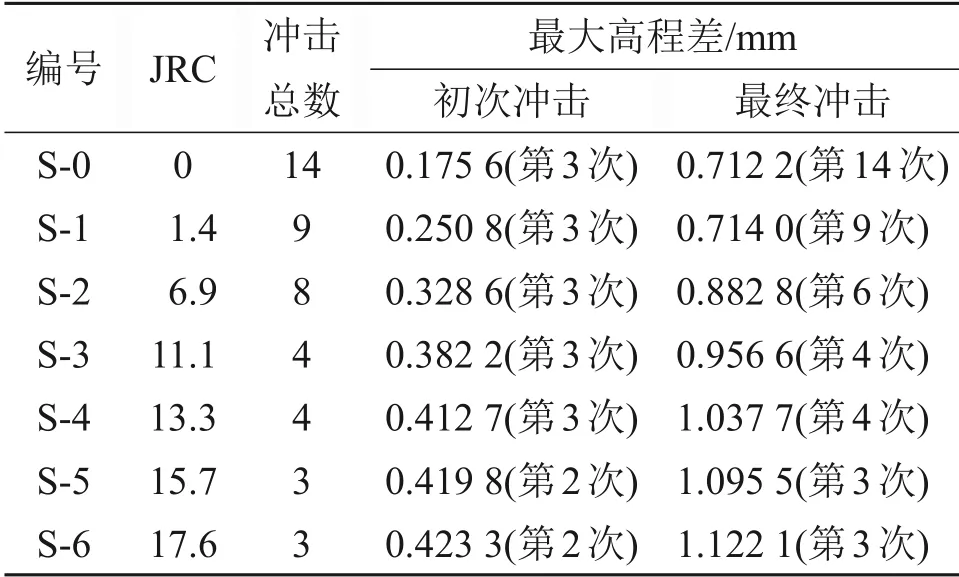
表2 试样冲击总数与冲击前后高程差Table 2 Impact number and elevation difference
3 结论
1)在循环冲击荷载作用下,当冲击次数不多且节理试样没有破坏前,节理法向刚度保持稳定,当冲击至节理面破坏然后出现裂纹时节理法向刚度减小约20%。
2)在循环荷载作用的初期与末期,节理粗糙度系数JRC与节理法向刚度均呈现负相关关系。节理法向刚度随节理粗糙度系数增加而降低。
3)节理试样破坏所需消耗的总能量随节理粗糙度系数的增加而减少。
4)当冲击次数较少时,冲击前后的节理表面形貌的变化很小,当冲击至节理试样破坏时,冲击前后的节理表面形貌发生明显变化。另外,随着JRC 的增大,冲击前后节理形貌的变化也有所增加。
需要指出的是,由于试验条件和节理面制作工艺的限制,此处的节理均为规则的锯齿状节理,但真实节理的表面形貌更为复杂。本文有关节理试样破坏的耗能分析较为理想,对于在冲击荷载作用下节理面上能量消耗的微观机理需要进一步的研究。
