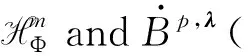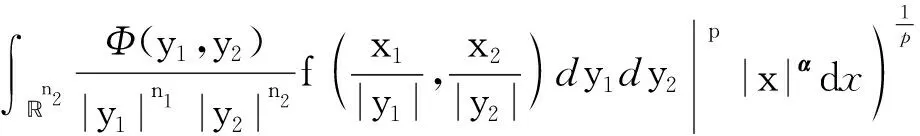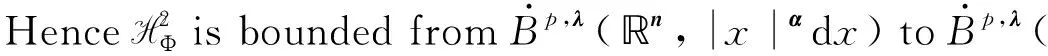Sharp bound of Hausdorff operators on Morrey spaces with power weights*
2021-09-26ZHANGXingsongWEIMingquanYANDunyan
ZHANG Xingsong, WEI Mingquan, YAN Dunyan
(1 School of Mathematical Sciences, University of Chinese Academy of Sciences,Beijing 100049, China;2 School of Mathematics and Statistics, Xinyang Normal University,Xinyang 464000, Henan, China)(Received 23 December 2019; Revised 2 March 2020)
Abstract In this paper, we calculate the norm of the Hausdorff operator HΦ defined on the Morrey space with power weights Lp,λ(n,|x|αdx) and the homogeneous central Morrey space with power weights n,|x|αdx), respectively. We also extend our results to the product Hausdorff operator
Keywords Hausdorff operator; product Hausdorff operator; Morrey space
Hausdorff operator[1]was first introduced in 1917. As is well known, the Hausdorff operator includes many famous operators such as Hardy operator, adjoint Hardy operator, Cesaro operator and Hardy-Littlewood-Polya operator (see the examples below). Especially, Hardy operator as a kind of very important average operator is widely studied by many mathematicians. Researchers have built a relatively complete and mature theory about Hardy operator. Naturally, an in-depth study on Hausdorff operator is of great significance. In the recent years, Hausdorff operator and its variations have been widely studied by many researchers. For example, Chen et al.[2-3]considered the boundedness properties of Hausdorff operator on Euclidean spaces, such as the Lebesgue spacesLp, the Hardy spacesHpand the Herz type spaces. For the sake of convenience, one can refer to Refs. [4-8] for more details of the recent progress on Hausdorff operators. In 2015, Gao et al.[9]studied the boundness properties of the (fractional) Hausdorff operators on the Lebesgue spacesLpwith powers. It is the starting point of our research.
1 Preliminaries and main results
We first recall the classical one-dimensional Hausdorff operator. For a function φ defined on+=(0,∞), the one-dimensional Hausdorff operator is defined by
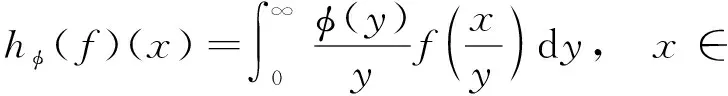
It is worth mentioning that if we choose differentφ, then we will get different operators. Here we present several important examples that have been extensively studied.
hφ(f)(x)=
Here, with the different choice ofφ,hφrepresents the famous Hardy operator, adjoint Hardy operator, Cesaro operator and Hardy-Littlewood-Polya operator, respectively.
High-dimensional Hausdorff operators have several versions (see Refs. [2,4,6]). In 2003, Anderson[10]studied then-dimensonal Hausdorff operator
where Φ is a function defined onn. In 2015, Gao et al.[9]studied the boundedness ofHΦon Lebesgue spaces with power weights and gave the sufficient conditions for the boundedness of the (fractional) Hausdorff operatorsHΦon the Lebesgue spaces with power weights. For some special cases, these conditions are sufficient and necessary.
In this paper we will consider the followingn-dimensional Hausdorff operator. Give a nonnegative function Φ defined onn. Then-dimensional Hausdorff operator is defined by
Our main purpose of this paper is to study the sharp bound of the Hausdorff operators HΦon the Morrey spaces with power weights.
Before stating our main results, we give some ordinary notations as follows. Fora∈nandR>0,Q(a,R) denotes the cube centered atawith side lengthRandB(a,R) denotes the ball centered atawith radiusR. For a nonnegative functionω,ω(A) denoteswherex∈n,Ais a measurable subset ofnand dxis the Lebesgue measure ofn.
Definition1.1Let 1≤p<∞,-1/p≤λ<0,ω=ω(x)=|x|αandα≥0. The Morrey space with power weightsLp,λ(n,|x|αdx) is defined by
Lp,λ(n,|x|αdx)
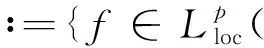
‖f‖Lp,λ(n,|x|αdx)<+∞},
where
‖f‖Lp,λ(n,|x|αdx)=
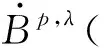
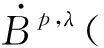
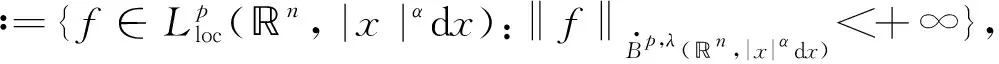
Now we formulate our two main results about HΦ.
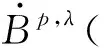
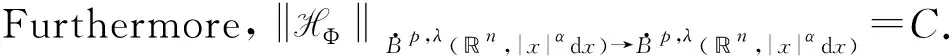
However, when we consider the boundedness of HΦonLp,λ(n,|x|αdx), we can only give a sufficient condition. Because of the appearance of power weights, the usual rotation method is not enough for us to get the necessary condition. Hence we state our partial result as follows.
Theorem1.2Let 1≤p<∞,-1/p≤λ<0 andα≥0. Then HΦis bounded fromLp,λ(n,|x|αdx) toLp,λ(n,|x|αdx), provided that
Proposition1.1Let 1≤p<∞ and -1/p≤λ<0. Then HΦis bounded fromLp,λ(n,dx) toLp,λ(n,dx) iff
Furthermore, ‖HΦ‖Lp,λ(n,dx)→Lp,λ(n,dx)=C.
Our results can be extended to product spaces. Letm,ni∈+,1≤i≤m.Φ(y1,…,ym) is a nonnegative function defined onn1×…×nm.The product Hausdorff operator is defined by
wherex=(x1,…,xm)∈n1×…×nmandy=(y1,…,ym)∈n1×…×nm.
For the sake of convenience, we use the following notations.
Letn=(n1,…,nm),n∶=(n1,…,nm).α=(α1,…,αm),|x|α=∣x1|α1…|xm|αm.
Correspondingly, we define the product Morrey spaces with power weights.
Definition1.3Let 1≤p<∞,m∈+,-1/p≤λi<0,λ=(λ1,…,λm),ωi(xi)=|xi|αi,αi≥0 and 1≤i≤m. The product Morrey space with power weightsLp,λ(n,∣x∣αdx) is defined by
Lp,λ(n,∣x∣αdx)

<+∞},
where
Definition1.4Let 1≤p<∞,m∈+,-1/p≤λi<0,λ=(λ1,…,λm),ωi(xi)=|xi|αiαi≥0 and 1≤i≤m. The product homogeneous central Morrey space with power weightsn,|x|αdx) is defined by
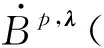
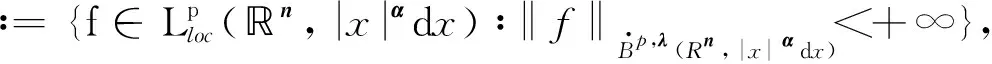
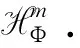
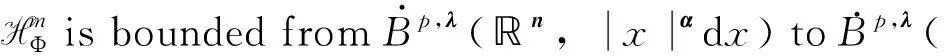
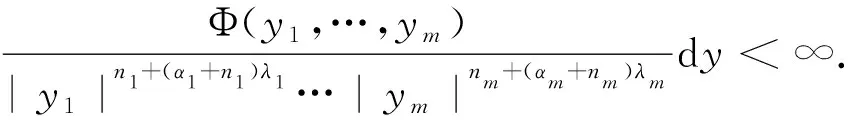
2 Proof of main results
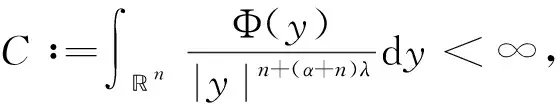

(1)
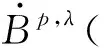
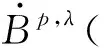
From (1), we can get that
(2)
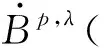
HΦ(g)(x)=Cg(x).
(3)
In fact, we have that
It follows that
It implies from (3) that
(4)
Combining (2) with (4) yields that
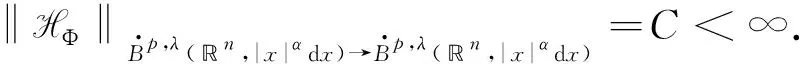
ProofofTheorem1.2Since
it follows from Minkowski inequality that
‖HΦ(f)‖Lp,λ(n,|x|αdx)
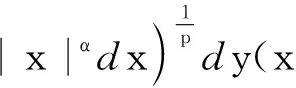
Hence HΦis bounded fromLp,λ(n,|x|αdx) toLp,λ(n,|x|αdx).
□
ProofofProposition1.1By Theorem 1.2 we merely need to prove the necessity. More precisely, we need to find a functiong∈Lp,λ(n,dx) such that
Takingg(x)=|x|nλ, by Ref.[11], we can easily checkg∈Lp,λ(n,dx). For the sake of completeness, we give the specific proof. We consider two cases:
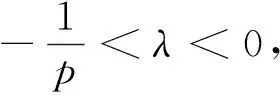
Case 2: if |a| <+∞. Hence,g∈Lp,λ(n,dx). Since HΦ(g)(x)=Cg(x), the proof is finished. □ ProofofTheorem1.3We just prove the theorem form=2. Form>3, the method is similar. We first prove the sufficiency. Then we get Next we prove the necessity. Take g(x1,x2)=|x1|(α1+n1)λ1|x2|(α2+n2)λ2. By the similar consideration and computation of the necessity of Theorem 1.1, we can obtain our conclusion immediately. □ ProofofTheorem1.4The proof of Theorem 1.4 is similar to the proof of Theorem 1.2, so we omit the details. □