近断层脉冲型地震动作用下黏滞阻尼器和双调谐质量阻尼器对曲线高墩刚构桥减震控制

肖 波，郑永瑞，王洪国，许维炳*，陈彦江，王少剑

(1.北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124；2.长春市市政工程设计研究院，长春 130012；3.山东高速临枣至枣木公路有限公司，枣庄 277100)

随着减隔震(振)技术理论不断发展，减震(振)控制研究不断深入，从航空航天、车辆机械、建筑结构、桥梁结构等领域不断丰富拓展。为了减小地震对桥梁结构的损坏，桥梁的减震(振)控制研究得到越来越多的学者关注，越来越多的减震控制措施应用到桥梁结构。山区高烈度高墩刚构桥设计复杂，易产生严重的震害[1]，且针对曲线高墩刚构桥的减震措施较少，既有减隔震措施对曲线高墩刚构桥的减震控制效果及参数影响规律尚不明晰。

黏滞阻尼器在桥梁结构中已有较多应用，诸多学者也通过数值模拟，试验研究方面对连续梁桥[2]、斜拉桥[3]、悬索桥[4-5]等进行了研究。王浩等[2]建立了某三跨隔震曲线连续梁桥的有限元模型，分析了黏滞阻尼器的参数变化对地震作用下结构动力响应的影响规律。李建中等[3]研究了黏滞阻尼器对千米级斜拉桥纵向减震效果，进行了某斜拉桥的1∶35相似比的全桥振动台试验模型，纵向采用黏滞阻尼器的减震体系可以显著减小结构动力响应，输入地震动的特性也会影响黏滞阻尼器的减震效果。陈彦江等[4]使用黏滞阻尼器对某自锚式悬索桥进行减震控制，阻尼器合理参数下，梁端、塔顶位移反应减小，主塔底部应力有所减小，证明黏滞阻尼器对悬索桥具有较好的减震效果。郭志明等[5]对使用柔性中央扣和黏滞阻尼器的悬索桥的组合试验的减震方式进行研究，认为黏滞阻尼器的减震效果远好于柔性中央扣，黏滞阻尼器的参数应综合考虑静力和地震响应优化确定。Liang等[6]研究了黏滞阻尼器和速度锁定装置等4种减震装置。对黏滞阻尼器的参数和安装位置进行了优化。现阶段研究成果表明黏滞阻尼器对直线桥梁具有较好的减震效果，但其对曲线桥梁的减震控制效果及参数影响规律研究仍十分有限，也缺少相关的应用案例。

调谐质量阻尼器时是另外一种在桥梁结构减震(振)控制中常用的减震装置。从调谐质量阻尼器(tuned mass damper，TMD)到多重调谐质量阻尼器(multiple tuned mass damper，MTMD)，再到调谐颗粒阻尼器(tuned particle damper，TPD)，调谐质量阻尼器在桥梁结构减震(振)控制中的理论研究和工程实践不断深入。Miguel等[7]将TMD和MTMD系统应用于车桥耦合振动中，在考虑路面不平整度及车辆变化等参数随机变化时，减振系统鲁棒性更优，减振效果较好。樊健生等[8]将人行荷载的功率谱密度转化为均方根加速度，将其作为目标函数，引入MTMD系统，基于理论计算进行系统优化，可有效提高人-桥-MTMD系统减振效率的鲁棒性，且同时满足了人行桥的舒适度要求。Zahrai等[9]对某斜拉桥通过OpenSees模拟，对减震系统的TMD基于遗传算法优化，并通过模糊逻辑控制确定最优减震效果，有效减小了跨中最大位移。某双层曲线斜拉桥的上层人行桥人致振动响应显著，华旭刚等[10]将上下两层引入连杆提高结构刚度，布置TMD减震装置，取得了较好减震效果。倪铭等[11]建立了简谐激励作用下DTMD控制体系(DTMD-SDOF)的运动方程，推导其动力反应放大系数，提出了针对DTMD的调优策略及优化评价函数，对不同参数对DTMD系统的共振峰值和调频宽度进行研究，认为DTMD比TMD和MTMD更具工程适用性。许维炳等[12]、Yan等[13]对大跨度的直线梁桥和曲线梁桥进行1∶10相似比的振动台模型试验，使用调谐型颗粒阻尼器(tuned particle damper，TPD)的不同参数变化进行了减震控制研究。将TPD力学模型简化DTMD，通过试验和理论计算认为颗粒阻尼器对桥梁具有一定的减震效果。对于曲线梁桥，TPD沿顺桥向和横桥向均能发挥一定的减震控制效果，对曲线梁桥动力响应的抑制具有良好的方向适应性。现阶段研究成果表明，调谐阻尼器可用于桥梁振动控制中，但传统单TMD对桥梁结构的地震响应控制效果不佳，而MTMD以及TPD等阻尼器的参数优化及设计方法复杂，其实际应用方法仍处于探索阶段。DTMD具有更优的鲁棒性，参数优化和设计方法相对简单，因此DTMD对曲线高墩刚构桥的减震效果值得进一步研究。

鉴于此，现基于OpenSees软件建立典型曲线高墩刚构桥的非线性分析模型，选取3条近断层脉冲型地震波作为输入，设计和优化几种较优参数的VD和DTMD，开展设置VD和DTMD前后的曲线高墩刚构桥时程分析。重点开展VD和DTMD减震设计参数对其减震控制效果的影响。相关成果可为VD和DTMD在曲线高墩刚构桥减震控制应用提供借鉴。

1 工程概况

1.1 工程概况

以夏沙高速沙溪大桥为例，沙溪大桥为高墩曲线刚构桥，跨径为(66+120+66)m，曲线半径为650 m，0#墩和5#墩高45 m，1#墩～4#墩高60 m，两道系梁分别编号X1、X2，设计荷载为公路-Ⅰ级。主梁截面为变截面连续刚构箱梁，采用C55混凝土。主墩为双肢薄壁，边墩为矩形空心截面，桥墩和系梁均采用C40混凝土。边墩与主梁之间的支座为单向盆式橡胶支座。图1(a)为全桥模型示意图，紫色为主梁部分，绿色为双肢薄壁主墩，蓝色为两墩之间的系梁，位于桥墩1/2处，红色为边墩。图1(b)为曲线高墩刚构桥的实桥照片。

1.2 基于OpenSees非线性模型建立

混凝土采用OpenSees材料库Concrete01本构。钢筋采用steel02本构。考虑到主梁在动力分析中一般不进入塑性状态，因此采用弹性梁单元elasticBeamColumn模拟。支座为橡胶盆式支座，采用零长度单元ZeroLength结合双线性滞回模型Hardening Material进行模拟。OpenSees模型中主梁以直代曲共80个节点，79个单元。桥墩采用考虑弹塑性的非线性梁柱纤维单元nonlinearBeamColumn，同时考虑P-Delta效应。桥墩、系梁由非约束混凝土、约束混凝土、钢筋3种纤维构成，桥墩和系梁纤维数分别含有186、206个。

图1 典型曲线高墩刚构桥Fig.1 Typical curved high pier rigid frame bridge

1.3 模型验证

为验证曲线高墩刚构桥模型的准确，分别在OpenSees、Midas中建立全桥模型，两者在结构整体参数大体保持一致。在Midas中使用PSC建模助手建模，主梁按照设计采用变截面组。OpenSees没有变截面单元，简化主要是以直代曲，现在取其前五阶模态进行对比，结果如表1所示。

由表1可知，两种模型频率在第一阶相差较大，在8.23%左右，但是在后几阶模态频率差别不大，都在10%以内，两者误差较小。分析产生误差的原因为：两者的截面单元不同，OpenSees在变截面单元处刚度存在变化，变截面处的节点质量与Midas相比发生了变化，单纯地认为两者模型节点的节点质量相同或许会对结果造成一定影响。

表1 模型前五阶模态对比Table 1 Comparison of the first five modes of the model

2 近断层地震动选取

由于高墩桥梁主要修建于山区，而近断层脉冲型地震动是山区地震中常见的地震动形式。因此，依据桥梁的桥址处场地条件和设防烈度(8度)，选取了3条近断层脉冲地震波TCU052、TCU065、TCU068作为输入。图2为选取近断层地震波的时程曲线(天然地震波加速度最大峰值)，加速度反应谱、速度反应谱和位移反应谱。

图2 3条地震波时程曲线Fig.2 Three seismic wave time history curves

3 黏滞阻尼器(VD)减震控制效果

3.1 VD参数

黏滞阻尼器一般由缸体、导杆、活塞、阻尼孔和黏滞阻尼流体材料等部分组成，利用Maxwell模型来模拟黏滞阻尼器。为了有效控制曲线高墩刚构桥边墩位移过大及边墩的碰撞影响，改善桥梁的受力，在边墩沿切向方向布置各2个，全桥共4个阻尼器。研究了阻尼器的黏滞阻尼系数c和速度指数a对曲线高墩刚构桥的地震响应的影响。其中黏滞阻尼系数c取值为500、1 500、2 500、3 500、5 000、7 000、9 000 MN·(m/s)-a，速度指数a取值为0.3、0.5、0.7、0.9。

对于黏滞阻尼器来说，其减震控制方向主要为单向，故主要对曲线高墩刚构桥进行单向激励以研究不同黏滞阻尼系数c和速度指数a参数变化下结构的动力响应规律。图3～图8分别为X向、Y向0#墩及1#墩的墩顶位移和加速度响应、墩底剪力和弯矩变化、系梁剪力弯矩变化等。

由图3可知，分析0#边墩X向结果得，相同c时，随着a的增加加速度逐渐减小，减震效果逐渐增大。a=0.3、0.5时，c逐渐增大，加速度增大；a=0.7时，加速度先减小后增大；a=0.9时，加速度未呈现明显变化。随着c逐渐增大，相同a时，位移逐渐增大，减震效果变弱。随着a增大，位移逐渐变小，当a=0.9时位移变化不大，结构位移基本呈线性变化。由图4可知，分析0#边墩Y向结果得，相同c时，随着a的增加加速度逐渐增大，减震效果逐渐变弱；a=0.7时，随着c的变化，加速度变化明显，a=0.3时，减震效果较好，但随着c的变化，加速度变化不明显。相同c时，随着a的增加位移逐渐增大，减震效果变弱；相同a时，随着c的增加位移逐渐减小，减震效果增强。

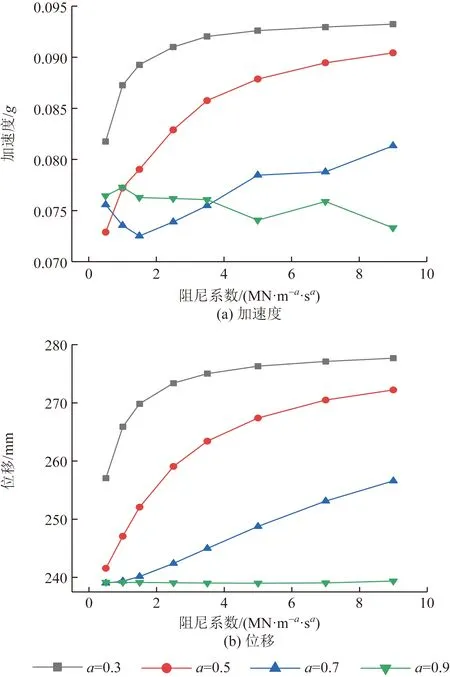
图3 0#墩X向加速度位移Fig.3 0# pier X acceleration displacement

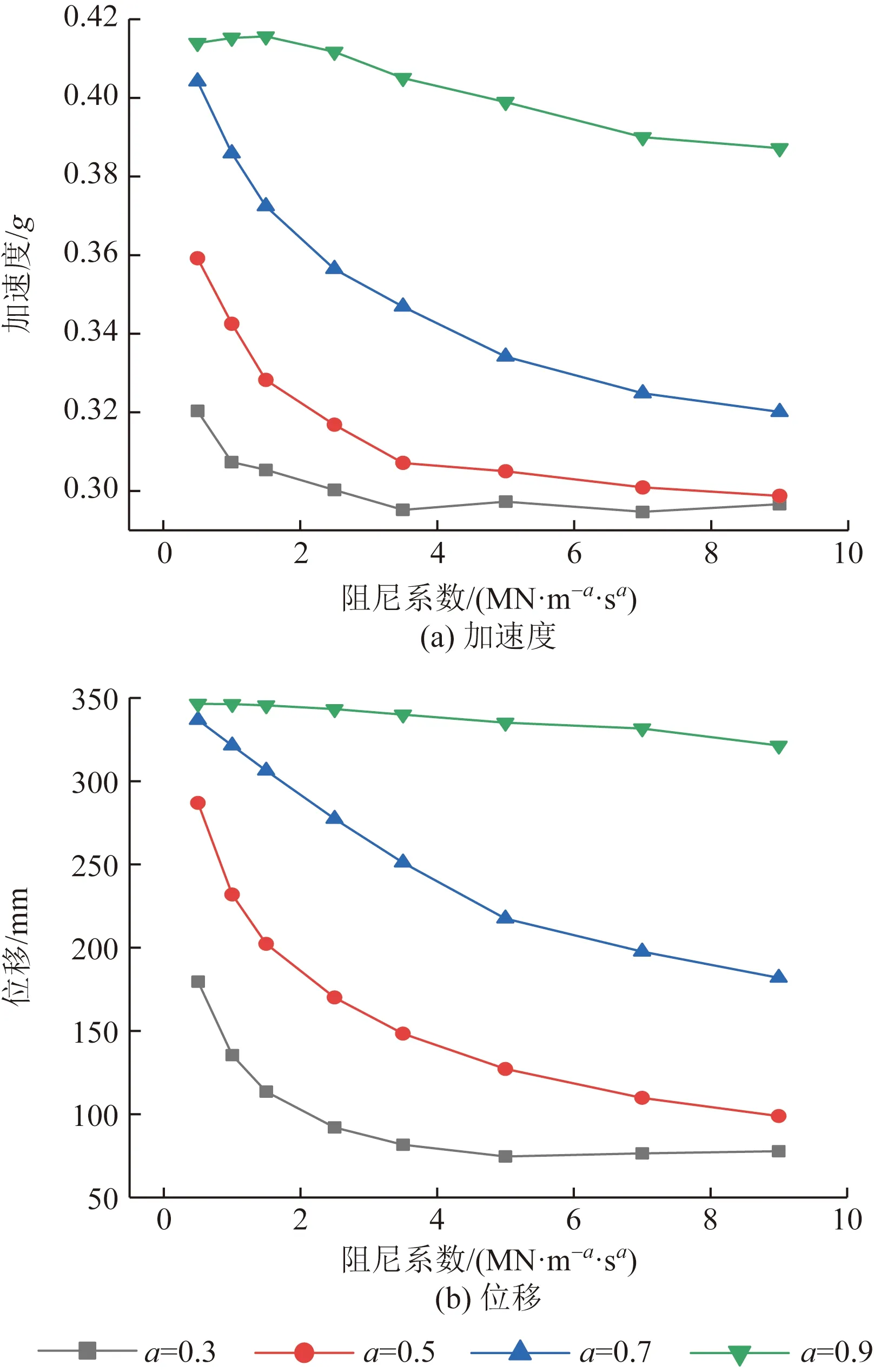
图4 0#墩Y向加速度位移Fig.4 0# pier Y acceleration displacement

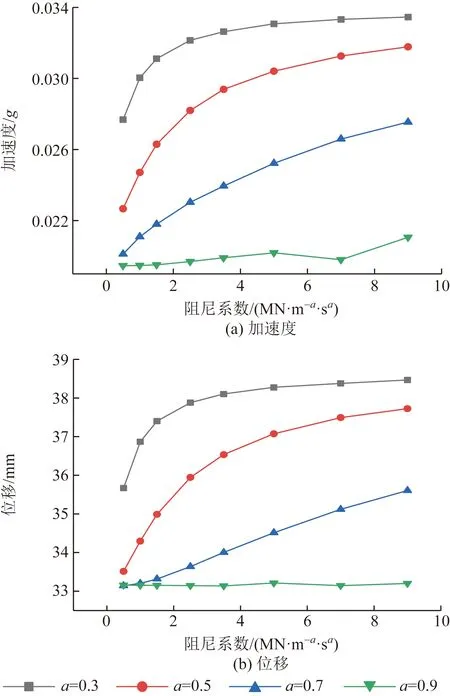
图5 1#墩X向加速度位移Fig.5 1# pier X acceleration displacement

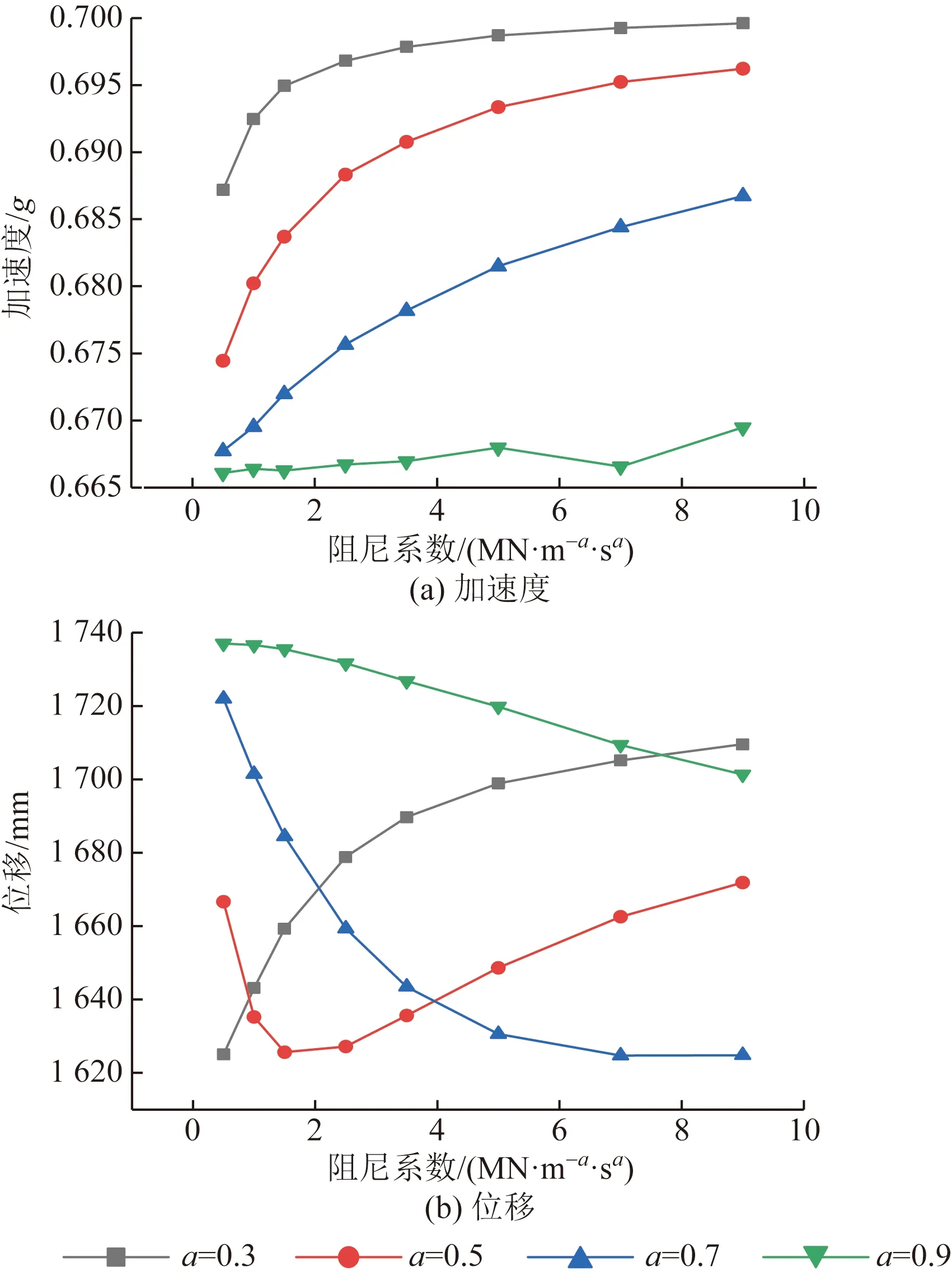
图6 1#墩Y向加速度位移Fig.6 1# pier Y acceleration displacement

由图5可知，1#中墩X向结果，相同c时，随着a的增加加速度逐渐减小，减震效果逐渐增大。a=0.3、0.5、0.7时，c逐渐增大，加速度增大，后逐渐趋于平缓；a=0.9时，加速度未呈现明显变化。由1#中墩X向的位移变化可知，随着c逐渐增大，相同a时，位移逐渐增大，减震效果变弱。随着a增大，位移逐渐变小，当a=0.9时位移变化不大，结构位移呈线性变化。由图6可知，1#中墩Y向结果，相同c时，随着a的增加加速度逐渐减小，减震效果逐渐增大。a=0.3、0.5、0.7时，c逐渐增大，加速度增大，后逐渐趋于平缓；a=0.9时，加速度未呈现明显变化。由1#中墩Y向的位移变化可知，a=0.3时，位移随c的增大而逐渐变大；a=0.5时，位移随c的增大先减小后逐渐变大；a=0.7、0.9时，c逐渐增大，位移减小，后逐渐趋于平缓。

由图7可知，对于墩底剪力、弯矩而言，相同c时，随着a的增加剪力逐渐增大，减震效果逐渐减弱。a=0.3、0.5、0.7时，c逐渐增大，墩底剪力减小；a=0.9时，墩底剪力未呈现明显变化。墩底弯矩与墩底剪力变化趋势大致相反，随着c逐渐增大，相同a时，墩底弯矩逐渐增大，减震效果变弱。随着a增大，弯矩逐渐变小，当a=0.9时弯矩变化不大，墩底弯矩呈线性变化。由图8可知，对于系梁剪力、弯矩而言，相同c时，随着a的增加系梁剪力逐渐增大，减震效果逐渐变弱；随着c的增加，系梁剪力逐渐减小，后逐渐趋于平缓，减震效果减弱；a=0.9时，减震效果随着c的变化，系梁剪力变化不明显。由系梁弯矩变化图可知，相同c时，随着a的增加弯矩逐渐增大，减震效果变弱；相同a时，随着c的增加，系梁弯矩逐渐减小，后逐渐趋于平缓。

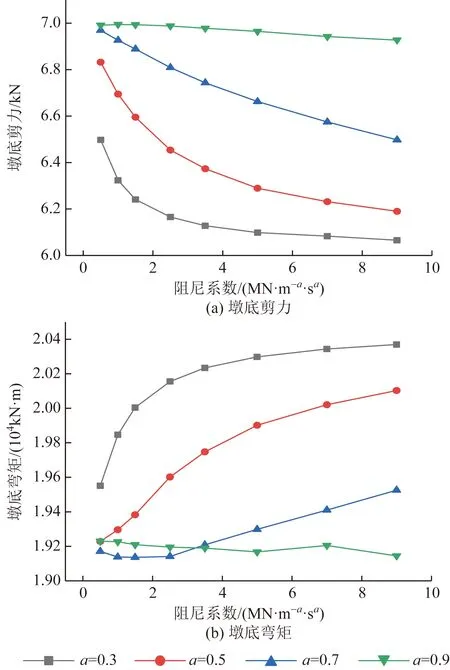
图7 墩底剪力与弯矩对比Fig.7 Comparison of shear bending moments at pier bottoms

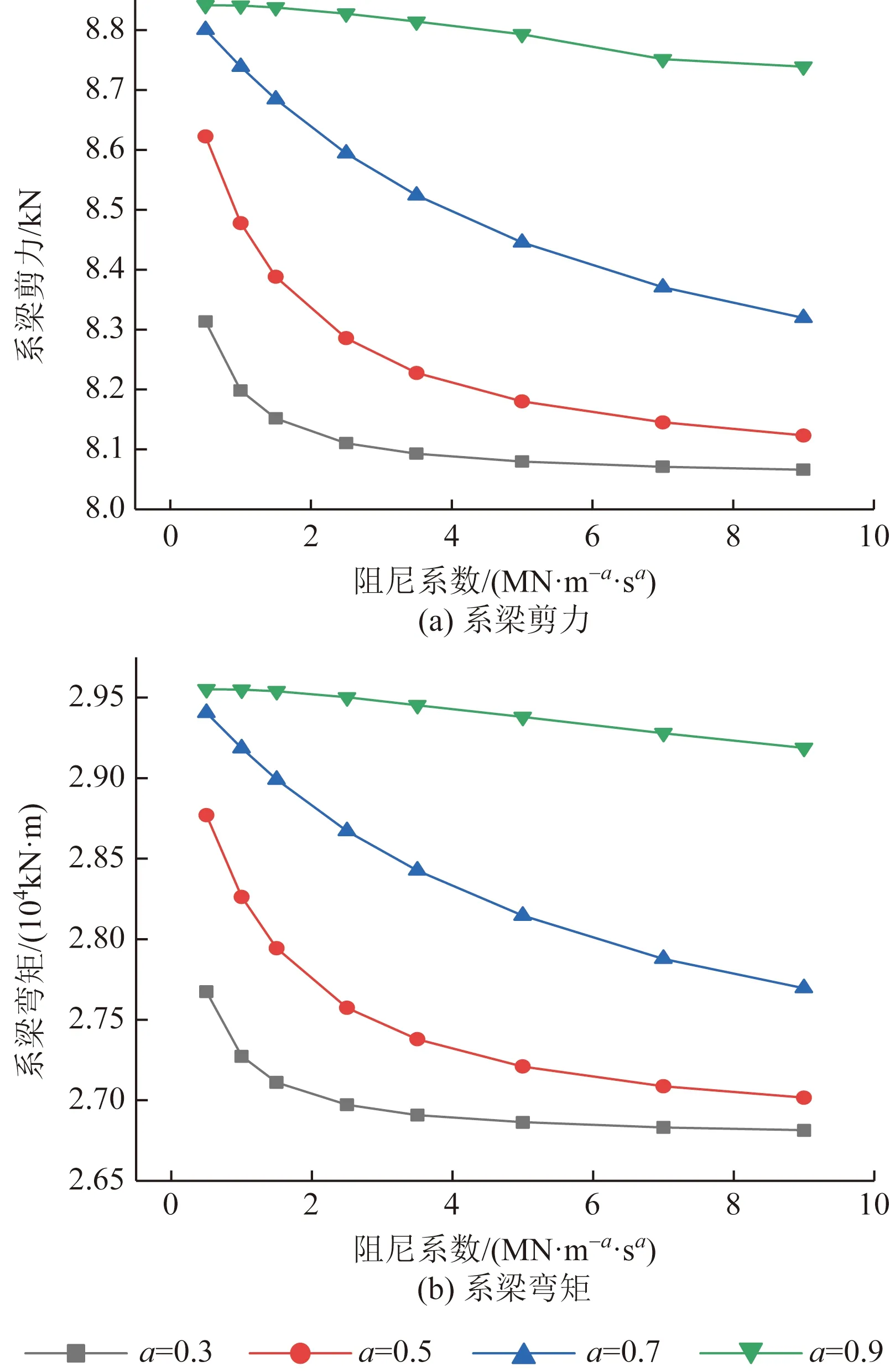
图8 系梁剪力与弯矩对比Fig.8 Comparison of bending moment and shear force of tie beams

3.2 减震效果分析

计算跨中墩顶位移的峰值位移的减震率，得出结构的最优参数，表2为不同阻尼系数和阻尼指数的减震率进行对比。

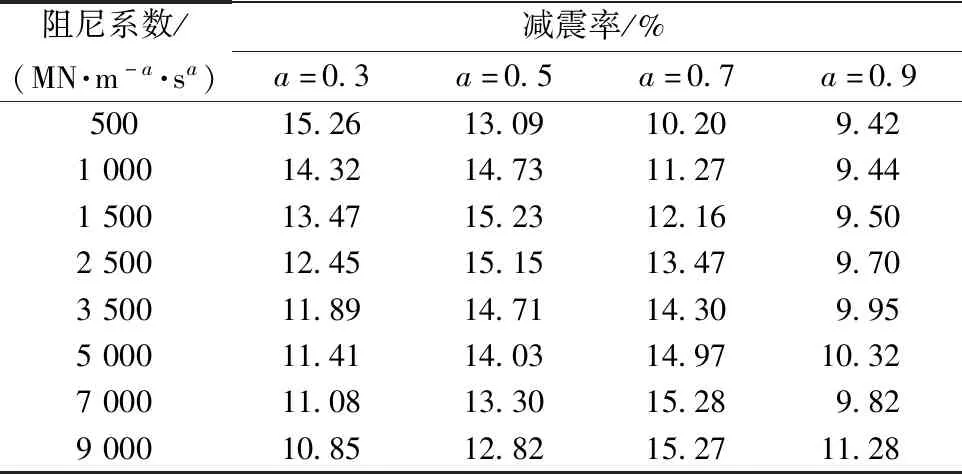
表2 不同参数减震率对比Table 2 Comparison of shock absorption rates of different parameters

由表2可知，随着阻尼系数的增加，对于不同的阻尼指数，结构墩顶位移的减震效果并不完全相同。相同c时，当a=0.3时，c越小减震效果越明显，最大为15.26%；当a=0.5时，减震率先增加后逐渐减小，最大为15.23%；当a=0.7时，减震率先增加后逐渐减小，最大为15.28%；当a=0.9时，为线性阻尼器，结构减震率逐渐增大。阻尼系数和阻尼指数变化时，结构减震率在9.42%～15.28%。近断层脉冲型地震动作用下，黏滞阻尼器对曲线高墩刚构桥的减震效果并不明显。分析原因可能是因为黏滞阻尼器为速度型阻尼器，近断层脉冲地震动具有很大的速度脉冲，而速度脉冲作用下黏滞阻尼器可能会出现锁定(lock-up)的现象，进而降低其减振控制效果。且曲线桥梁在单向地震作用下也表现出多向运动的特点，仅在边墩位置的切向方向设置黏滞阻尼器，具有一定的控制效果方向局限性。

4 双调谐质量阻尼器(DTMD)减震控制效果

DTMD由两个TMD串联而成，图9为DTMD的理论模型(主结构为单自由度结构时)。

4.1 DTMD减震原理

DTMD的动力方程为

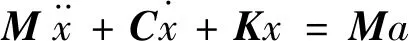
(1)

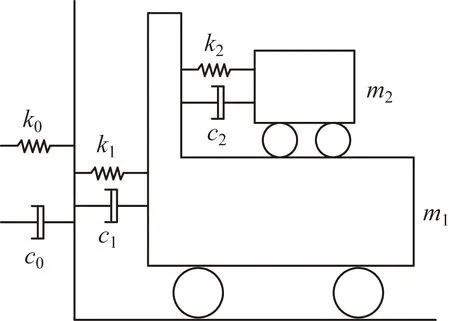
m1、k1、c1分别为上层子结构质量、刚度和阻尼；m2、k2、c2分别为下层子结构质量、刚度和阻尼图9 DTMD理论模型Fig.9 DTMD theoretical model

以单自由度为例可以得到受控结构在简谐激励作用下的结构位移放大系数(displacement magnification factor，DMF)，参数包含：

(2)

4.2 DTMD参数

文献[11]中给出了结构阻尼比ζ0=0.02，总质量比μ=0.05的最优参数，利用程序探索得到了DTMD的全局最优参数：μ′=0.13，ζ1=0，ζ2=0.24，λ1=1.01，λ2=0.89，P=4.415 3。并对ζ1、ζ2、μ′、λ1、λ2等参数进行寻优处理，得出不同参数的条件最优参数。采用结构阻尼比ζ0=0.05，总质量比μ=0.05，得出的全局最优参数为μ′=0.16，ζ1=0，ζ2=0.27，λ1=1.00，λ2=0.85，P=3.458 9。

通过4.1节公式利用MATLAB进行对MTMD参数寻找最优解，图10为DTMD系统不同参数变化下DMF与调节频率之间的关系。结构DMF主要与子结构质量比、子结构频率比、子结构阻尼比有关，同时还与最值及时间间隔有关系。

4.3 减震效果分析

为研究双调谐质量阻尼器对曲线高墩刚构桥的减震效果进行分析，分别给出了4个参数ζ2、μ′、λ1、λ2，共9组工况的减震结果。在两桥墩上方布置2个DTMD，桥墩上方空间大，可灵活布置阻尼器。计算了阻尼器的各设计参数，在OpenSees中选取合适的材料及单元。DTMD的单元长度设定较小，便于计算收敛，单元采用简单的非线性梁柱单元，阻尼器材料仍然使用Maxwell阻尼材料，可提供刚度及阻尼材料，收敛性能较好，且当c为零时，设定一个较小值可以满足要求。速度指数为1，设定为线性阻尼器。

表3为不同工况阻尼器计算参数，为从图10选取的几组计算的DTMD参数。图11为DTMD几种参数变化的工况(9组工况为计算的参数，分别编号C1～C9，第10种为相同质量比的TMD，编号C10)在近断层地震波激励时墩底剪力、系梁剪力弯矩，X向、Y向的墩顶加速度、墩顶位移响应结果。

图10 DTMD系统参数分析Fig.10 DTMD system parameter analysis

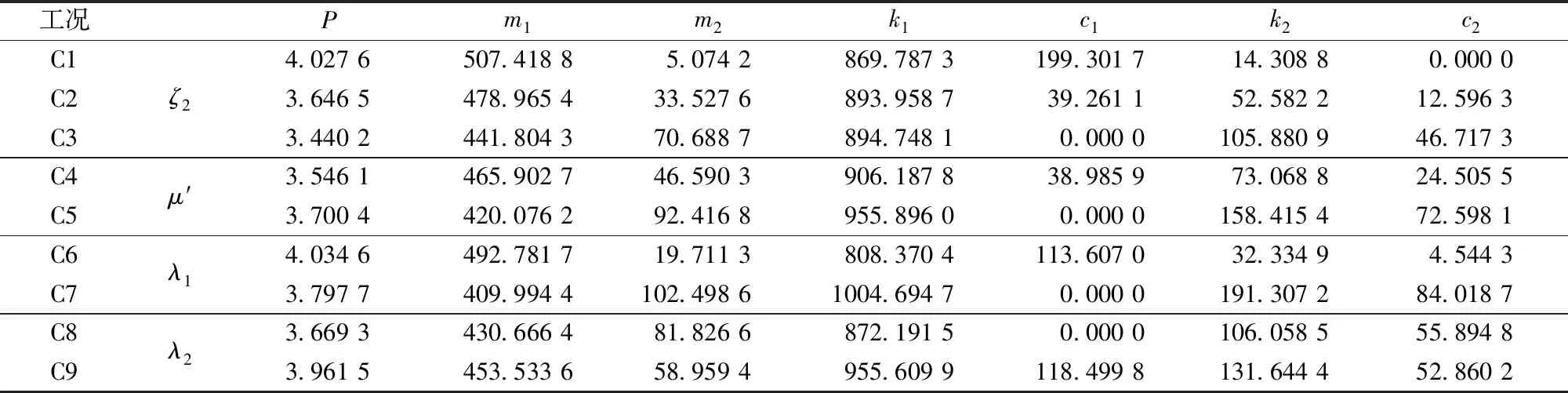
表3 不同工况阻尼器计算参数Table 3 Calculation parameters of damper in different working conditions

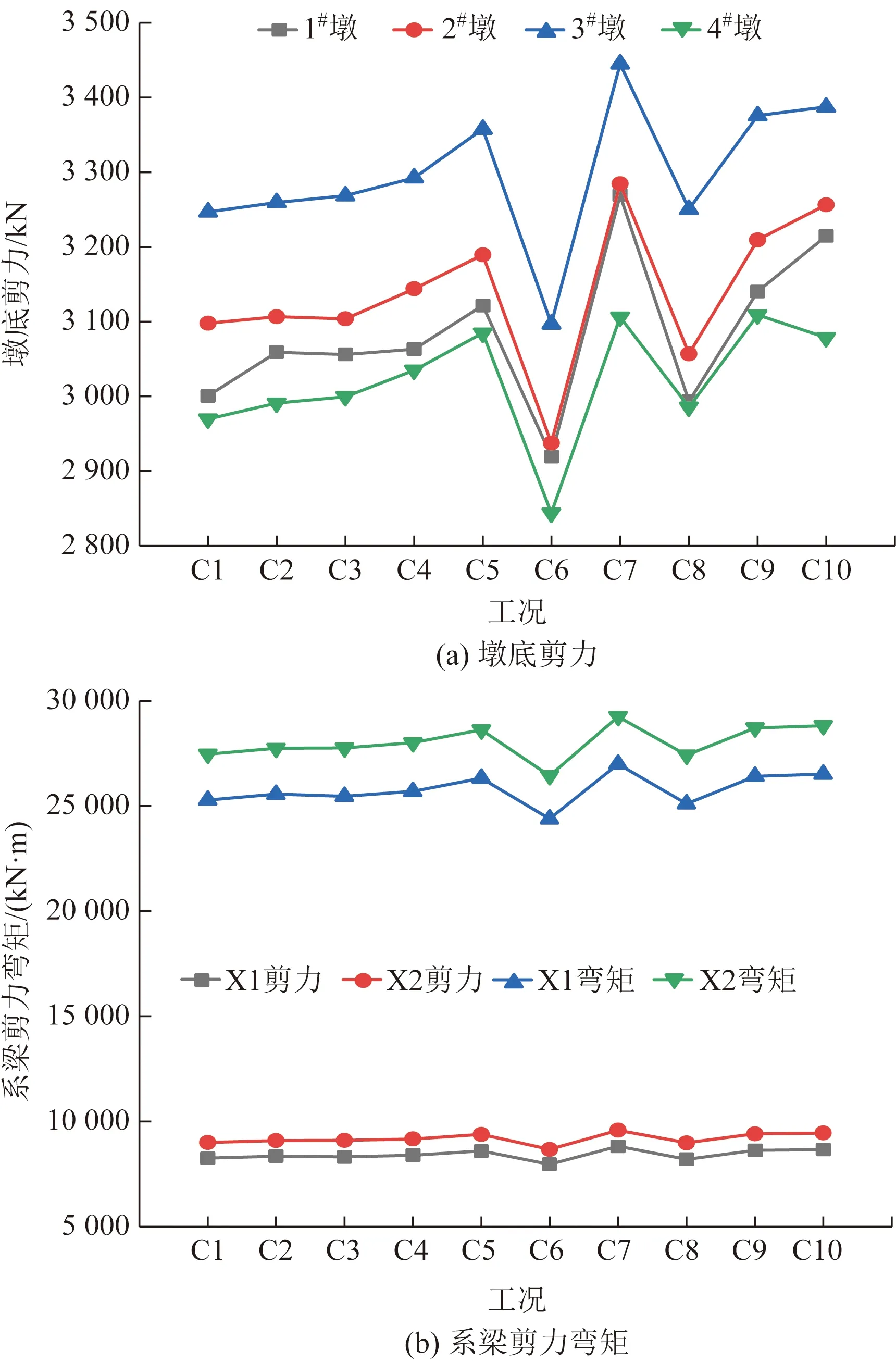
图11 DTMD控制下结构内力Fig.11 Structural internal force under DTMD control

由图11(a)可知，DTMD对墩底剪力减震效果明显高于相同附加质量比下的TMD，而相对无减震条件下的墩底剪力(约7 400 kN),DTMD的减震率高达45%左右。由图11(b)可知，系梁剪力弯矩与墩底剪力的变化趋势相同。相对未减震时的墩底内力(剪力22 505 kN，弯矩69 190 kN·m),DTMD的减震率在40%左右，减震效果较好。

由图12(a)可知，DTMD墩顶加速度减震效果部分高于相同质量比的TMD，而相对无减震条件下的墩顶加速度响应(X向0#墩0.58g、X向1#墩中0.59g、Y向0#墩0.49g、Y向1#墩0.51g),DTMD的减震率大多在55%左右。由图11(b)可知，DTMD控制下墩顶加速度与墩顶位移的变化趋势相同。相对未减震时的墩顶位移峰值(X向0#墩2 005 mm、X向1#墩2 094 mm、Y向0#墩519 mm、Y向1#墩1 614 mm),DTMD的墩顶位移减震率大多在75%左右，减震效果较好。

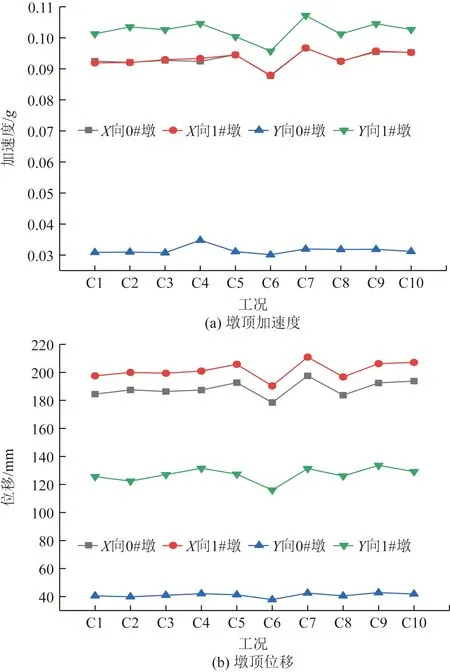
图12 DTMD控制下结构加速度和位移Fig.12 Structural acceleration and displacement under DTMD control

由图11、图12可知，DTMD具有较好的减震效果，结构内力减震率在45%左右，结构位移、加速度响应减震率在55%～75%范围内，DTMD对曲线高墩刚构桥减震控制效果较好。需要指出的是数值分析结果与理论分析结果存在一定的差异，分析原因是DTMD的布置位置、分布数量等对其减震控制效果存在影响。

5 结论

以近断层脉冲型地震动作为输入，通过数值仿真分析探究了黏滞阻尼器(VD)和双调谐质量阻尼器(DTMD)对曲线高墩刚构桥地震响应的减震控制效果。主要结论如下。

(1)明晰了黏滞阻尼系数和速度指数对VD控制下曲线高墩刚构桥近断层地震响应的影响。在选取的黏滞阻尼器参数范围内，以墩顶位移为例，黏滞阻尼器的阻尼系数、速度指数对结构的减震控制规律如下：当a=0.3时，c越小减震效果越明显，最大减震率为15.26%；当a=0.5时，减震率先增加后逐渐减小，最大为15.23%；当a=0.7时，减震率先增加后逐渐减小，最大为15.28%；当a=0.9时，最优减震率仅在9.42%左右。

(2)揭示了阻尼比、质量比、频率比等参数对DTMD控制下曲线高墩刚构桥近断层地震响应的影响。较优设计参数条件下的DTMD对曲线高墩刚构桥的地震响应具有良好的控制效果(结构内力减震率达45%，加速度和位移减震率在55%～75%)，且与TMD相比，DTMD的鲁棒性更优，减震控制效果更好。DTMD系统可用于曲线高墩刚构桥减震控制中。