基于自适应神经网络的云资源预测模型

王悦悦，谢晓兰，郭 杨，覃承友，陈超泉

(桂林理工大学信息科学与工程学院，桂林 541006)

目前，以Docker和Kubernetes为主流的容器云平台因其运维自动化、部署简单方便和资源动态调度的特点而广受好评。作为云平台中重要的容器编排工具，Kubernetes需要将各种云资源合理均衡地分配给各个容器，以保证容器中的虚拟机可以及时地对云用户申请的云服务请求作出响应。可当云平台在短时间内需要响应大量服务请求时，Kubernetes内部的资源分配策略无法均衡准确地调度云资源，容易产生过度供应或者供应不足的情况，从而导致资源利用率差、请求响应不及时等问题[1]。

为了能更好地解决以上问题，需要让Kubernetes在提前知道资源需求的情况下进行更精准均衡的调度和分配云资源，从而可以让容器中的虚拟机能够及时、准确地对任务请求做出响应。所以，资源预测是让Kubernetes合理均衡地调度和分配资源的关键方法。

近年来也有不少学者关于资源预测提出了有效的实现方法和预测模型。传统的预测模型多采用神经网络和机器学习等方法[2]。Li等[3]将执行时间分成动态的和静态的，然后使用反向传播(back propagation，BP)神经网络从历史数据中预测未来时刻的动态执行时间；Mason等[4]利用智能算法全局寻优的特点去优化递归神经网络，经试验证明，优化模型可在短时间内甚至极端变化情况下预测CPU使用率；徐翔燕等[5]提出通过赋权值构建基于GM(1,1)和支持向量机(support vector machine，SVM)的组合预测模型，使用标准差法确定两种单一模型的权值，实验表明组合模型的预测效果优于单一模型。

有学者表明，云资源的数据序列和时间有着一定的关系[6]，也有不少学者使用时间序列模型进行处理。Chen等[7]提出先对历史数据进行了一种预处理，即通过经验模态分解法将不同频率的数据分离开来，然后将分解后的趋势项和残差项分别使用差分自回归移动平均模型(autoregressive integrated moving average mode，ARIMA)进行预测；Kumar等[8]考虑到中长期时间序列数据，使用了长短期记忆(long short-term memory，LSTM)网络模型对云系统的负载资源进行预测，并取得了一定的效果；韩朋等[9]为长短期记忆网络加入注意力机制，不仅能够处理时间序列变量，还可以对长短期记忆网络的权重进行优化，提高模型的准确度。

为了能够及时准确地对大任务量的请求作出响应，同时避免因资源供应不均衡而造成的资源浪费和服务水平协议(service-level agreement，SLA)违约情况，一个合理且效果良好的资源预测模型是非常有必要的[10]。针对以上情况，现提出一种基于改进卷积神经网络和长短期记忆网络的云资源预测模型，使用融合卷积神经网络(convolutional neural network，CNN)和长短期记忆网络特点的联合模型去预测容器云资源未来时刻的情况，同时自适应调整模型学习率的变化情况，使其适应模型需要，提高模型的预测精度。

1 卷积神经网络

卷积神经网络是一种可以同时学习众多特征的深度神经网络，目前已被广泛应用到图像处理、语音识别和资源预测等方面。一个卷积神经网络可由一个或多个卷积层、池化层、全连接层组成[11]。一般使用一维CNN处理时间序列数据和自然语言任务就能得到很好的效果，二维CNN多用于图像处理方面，能很好地提取图像特征。因此，选择一维卷积神经网络，其结构如图1所示，其中，sample指输入数据的样本数，step指数据的维度。

CNN的一大特点就是其内部的卷积层与池化层的共同配合作用，这种配合使得CNN能充分地学习总结历史数据内部的抽象特征信息。从图1中可以看到，一组时间序列数据需要先转化成卷积神经网络易处理的矩阵形式再传入卷积层；卷积层中，使用事先指定类型的卷积核对输入信息进行卷积计算，激活时序数据的特征，根据卷积核的数量可以提取时序数据的多层特征信息；紧接着，将提取的特征信息传入池化层进行信息的再采样，此时每层信息经池化层的“总结”转为序列更短更精细的信息数据；最后，数据进入全连接层，将多维的输入一维化。根据不同的需求将此操作反复不同的次数，即可实现对数据的充分学习。对于特征信息的提取可由式(1)计算得到，即

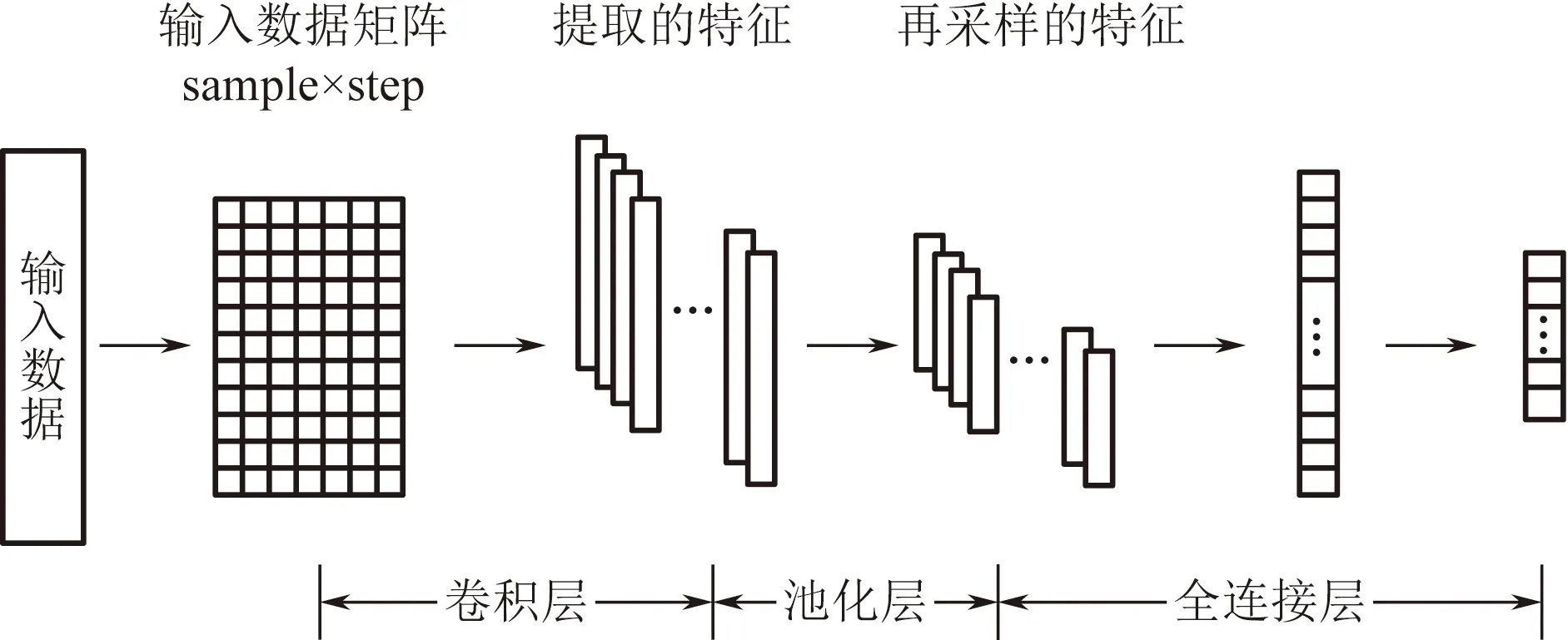
图1 一维CNN结构Fig.1 One dimensional CNN structure

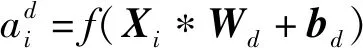
(1)

除了特殊的网络结构之外，CNN还具有权值共享的特点。不同的神经元之间共享同一个卷积滤波器的参数，可选择多种滤波器进行多种特征的并行卷积学习，可以极大地减少网络中冗杂的参数，避免模型的过拟合现象。

2 长短期记忆网络

长短期记忆网络可以对云资源的历史时间序列进行长短期相关性的学习[12]。相比传统的循环神经网络，其内部增加的“门”结构可避免对中长期时间序列学习所造成的梯度消失或者梯度爆炸现象。LSTM网络的一个记忆单元包括遗忘门、输入门、输出门和单元状态4个关键元素[13]，其网络结构如图2所示。

图2 LSTM网络的记忆单元结构Fig.2 Memory unit structure of LSTM network

当历史序列x(t)与上一时刻的输出h(t-1)组合进入LSTM网络中时，网络中记忆单元开始对数据进行学习，各“门”结构开始展开工作。计算新进入的序列信息是否有用，只有符合规则的信息 才会被留下，不符合算法规则的信息就会被遗忘门遗忘。留下的有用信息和输入门的信息进行规则组合，并且与这一时刻输出门所计算得到的输出O(t)共同作用得到了此时刻记忆网络的输出信息h(t)。众多神经元如此反复进行学习，LSTM网络便可以“记住”时间序列上的有用信息，从单元状态中丢弃部分无用信息[14]。其学习过程中各关键元素的计算公式如式(2)～式(7)所示。

ft=σ(Wf[ht-1,xt]+bf)

(2)

it=σ(Wi[ht-1,xt]+bi)

(3)

ot=σ(Wo[ht-1,xt]+bo)

(4)

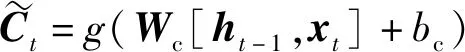
(5)

ht=ot*g(Ct)

(6)

(7)

式中：Wf、Wi、Wo、Wc分别为遗忘门、输入门、输出门和单元状态的权重矩阵；bf、bi、bo、bc分别为遗忘门、输入门、输出门和单元状态的偏置值；σ、g为两种激活函数，可根据需要选择效果较好的函数；·为点乘运算；*为卷积运算。

3 基于自适应神经网络的云资源预测模型

3.1 模型设计

传统的组合预测模型多采用权重赋值的方法，对不同的单一模型根据其预测情况赋权值[15]，然后对两个或多个单一模型进行组合预测，虽然取得一定的效果，但是每个模型在整个数据上的学习能力不断变化，使用固定的权重会影响模型整体的效果，而且选择一个合适的权重也是一个具有挑战性的问题。虽然后来有众多学者针对权重的选取做了一些研究，但是总体工作量较大，也无法保证固定的权重在整个模型训练中能表现出同样的优势。

因此，选择为LSTM网络增加卷积层的方式来进行时序数据的学习，通过融合两个不同的神经网络的特点，让模型充分挖掘历史时间数据中的特征信息，从而达到更好的效果。

传统的LSTM网络虽然可以学习中长期时间序列的数据特征，但是大规模的数据在长期的时序学习中会导致遗忘门“遗忘”部分有用的信息，造成网络学习效果退化。而卷积神经网络中特殊的卷积层可以对历史数据挖掘更多更深层次的特征信息。因此，在数据进入LSTM网络之前，先利用卷积神经网络中的卷积层对数据信息进行充分的挖掘和学习，使时序数据中的特征充分显现，然后再传入LSTM层进行时间相关性的学习，使模型能够更加准确的预测未来某一时刻的数据。融合CNN和LSTM网络特点的联合模型(convolutional neural network and long short-term memory network，CNN-LSTM)的网络结构如图3所示。

图3 联合模型网络结构图Fig.3 Network structure of union model

从图3可以看到，选择两个卷积层进行前期的特征学习，充分学习到数据的特征信息后进入池化层进行特征总结，flatten层用于将池化层的输出降维至一维，以此来适应LSTM层的输入格式。最后将卷积神经网络处理后的输出数据再作为LSTM网络的输入，进行时间相关性的学习。因为前期CNN已经利用卷积层和池化层输出了更多复杂特征的激活映射，所以LSTM网络便能够学习到时序数据上更为隐蔽的信息，从而提升模型效果，增加模型预测精度。

3.2 自适应学习率

学习率(learning rate，lr)是神经网络中影响较大的一个超参数，极小的变化都能够影响神经网络的学习效果[16]。自适应学习率可以让神经网络在训练过程中根据网络的训练情况对学习率进行调整，使其能够达到更好地训练目标。以损失函数作为参照函数：当损失函数的下降率趋于稳定，可以减小学习率衰减的速度，让网络进行全局范围内寻优；当损失函数值下降逐步降低，甚至开始出现震荡，可以不断减小学习率，使用较小的学习率进行探索，提高网络整体的收敛性。

针对学习率的以上特点，以损失函数值是否出现震荡为指标将神经网络的训练期分为两段：训练前期，损失函数值没有震荡情况，此时指标flag为0，这时根据损失函数值的变化量来适当加快或减慢学习率的衰减速度，保证神经网络的收敛速度；当损失函数值出现震荡，此时flag为1，训练进入后期，模型趋于收敛，使用较小的学习率并逐步递减，提高模型的预测精度。

考虑到训练前期损失函数值稳定下降，其变化量对于学习率的衰减速度具备有效的影响，因此训练前期，以损失函数值的变化量为自变量给出学习率的衰减系数，利用损失函数值的变化量判断模型的学习状态，使学习率呈现先快速减小再缓慢减小的趋势，从而让模型可以在不同的状态中具有不同的学习能力。但是训练后期的时候，损失函数出现震荡情况，其变化量不具备有效影响，通过让学习率根据世代(epoch)的变化动态调整为较小的值，可更大地满足模型的需求。综上，学习率计算公式为

(8)

式(8)中：ΔL为损失函数值的变化量；e为自然常数；∂为一个常数，代表了模型训练后期学习率下降的初始值，根据模型实际训练情况调整数值，令其为0.001。

为了更直观地体现出学习率在整个训练期的自适应调整情况，以其中一次的学习率变化为例，如图4所示。

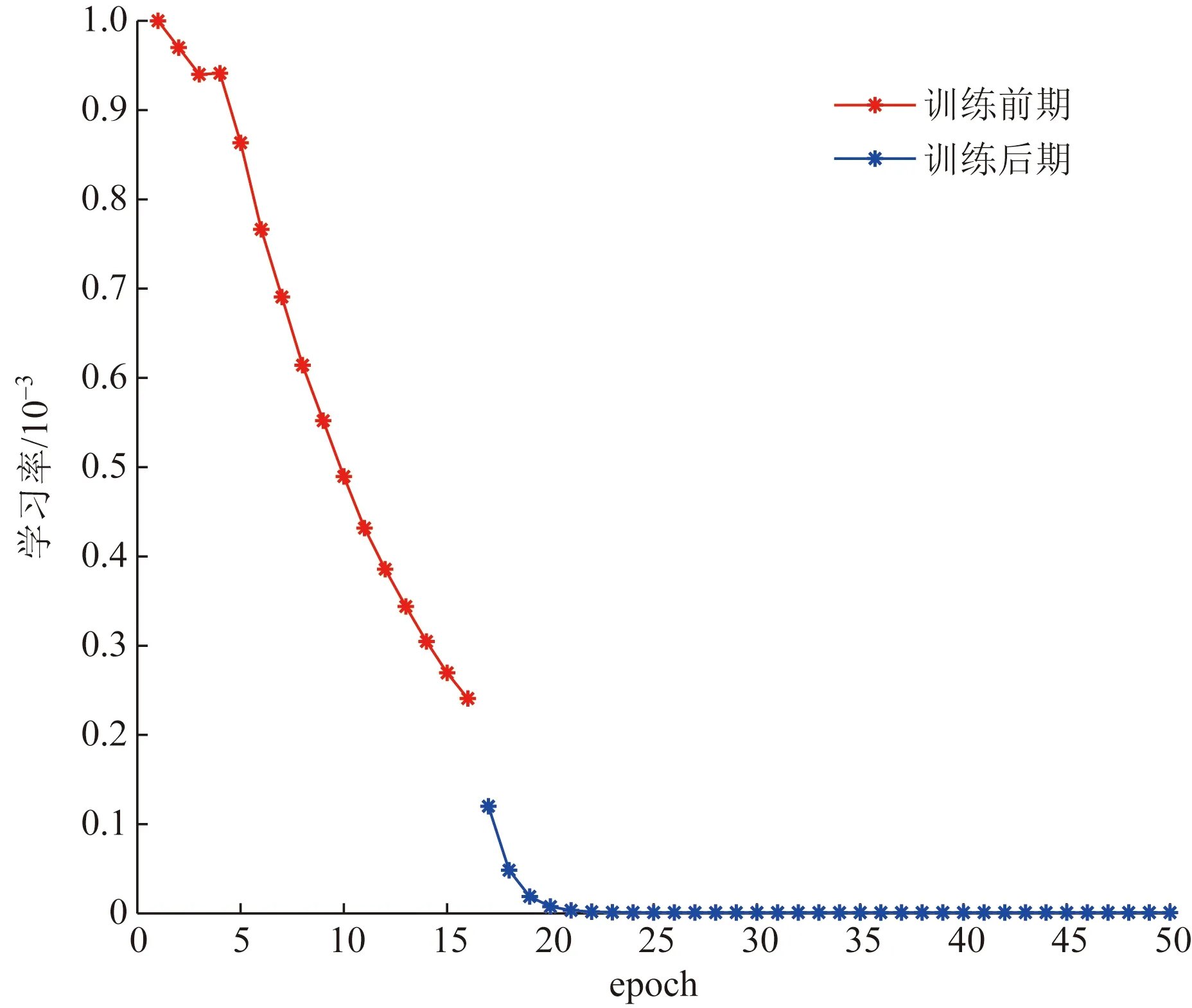
图4 训练期的学习率变化情况Fig.4 Changes of learning rate during training period

从图4中可以看到，学习率在训练前期稳定下降，衰减速度相对稳定，神经网络持续全局寻优来优化模型；大概第17个世代时，模型出现震荡，神经网络转为局部寻优，此时学习率骤减，并使用较小的学习率缓慢减小以保证模型寻得更优值，达到更高预测精度的要求。

4 实验结果及分析

实验使用Win10操作系统，Intel(R)Core(TM)i7-9750H CPU @2.60 GHz 2.59 GHz,8 GB内存，深度学习调用以Tensorflow1.2.1为后端的Keras模块。

为了检验所提模型的效果，选取传统的单一模型CNN、考虑时间相关性的单一模型LSTM、以文献[5]方法为基础进行赋权值的组合模型和未进行学习率改进的联合模型(CNN-LSTM)作为对比，将以上4种模型与所提模型(ICNN-LSTM)进行比较试验。考虑到模型权值随机，预测结果具有偶然性的可能，对比实验对每个模型独立测试10次，分别记录模型预测数据，根据模型测试数据，计算10次所得到的平均值作为最终结果进行对比分析。

4.1 实验数据和参数设置

实验数据集选取Microsoft Azure跟踪的公开发行版，内容是2017年的某一服务中的虚拟机工作负载跟踪，记录时间为30 d，记录间隔为5 min。因为需要分配的资源中CPU资源对资源调度和请求响应效果的影响较大，故以CPU使用率的变化情况为例进行测试，选取数据集的前25 d进行训练，最后5 d进行测试。在使用神经网络学习之前，需要先对实验数据进行缺失值处理和重复时间戳处理，以保证完整的时间序列数据。同时为了避免不同的量纲对测试实验造成任何消极的影响，统一对数据进行了归一化处理。

对神经网络的参数进行多次实验调整选取较优的一组参数，同时为保证对比实验的有效性，实验对所有对比模型的固定参数采用相同的值进行测试：卷积层的filters为32，kernel size为3，LSTM层的单元数为50，批处理数为32，激活函数使用RELU函数，并且统一使用Adam优化器进行模型处理。

4.2 预测结果分析

首先将5种模型的预测值与实际值进行对比，观察模型的总体预测情况，如图5所示。选取数据集的间隔时间为横坐标，CPU使用率的值为纵坐标，而且为了避免模型预测结果的偶然性造成的误差，每个模型单独测试10次之后的平均值作为最终的预测结果。

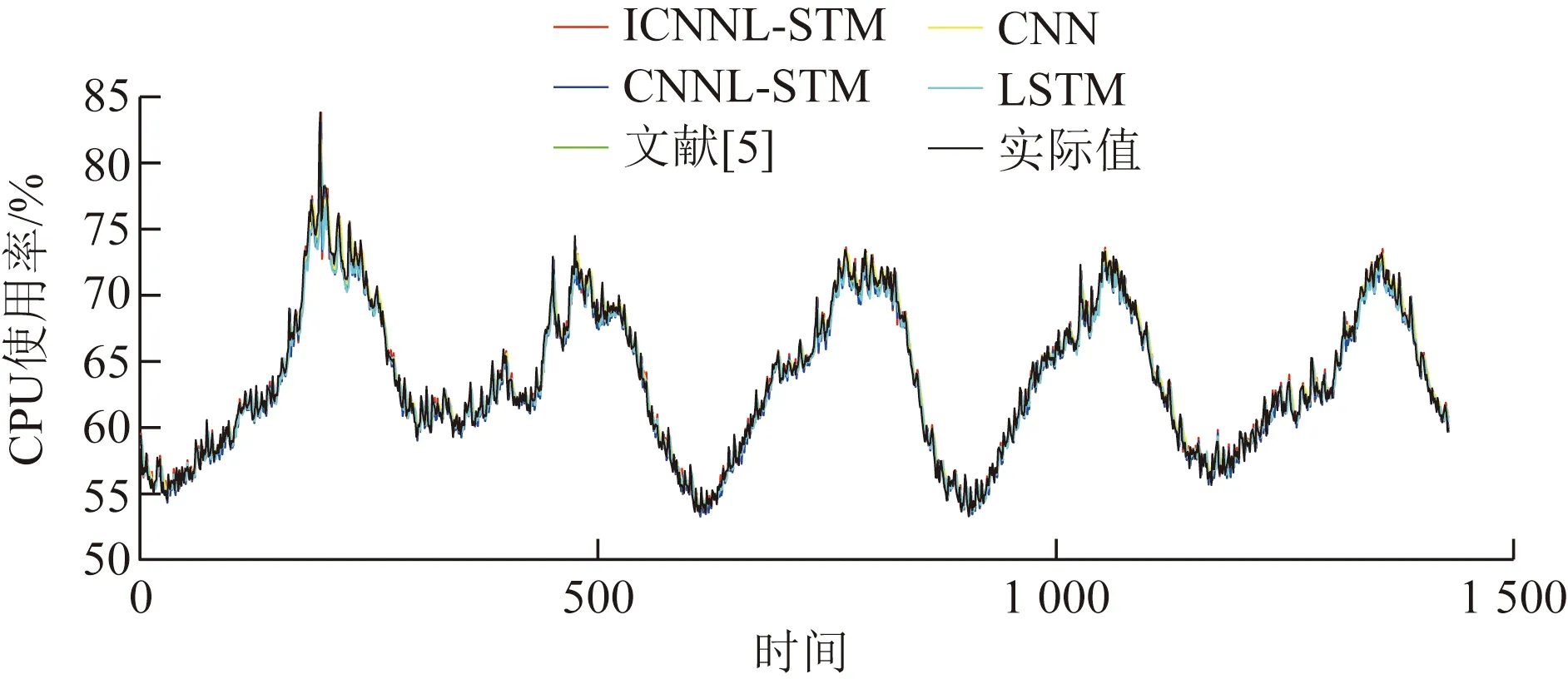
图5 5种模型的预测值与实际值对比图Fig.5 Comparison of predicted value and actual value of five models

如图5所示，5种模型都大致预测出时间序列未来一段时间的变化情况。LSTM、CNN和文献[5]的预测模型都能大致预测出数据的走向，但是在大部分峰值处的表现较差。以极端情况第197个时间采样点为例，实际CPU使用率为83.81%，LSTM、CNN和文献[5]的预测结果在78%左右，而CNN-LSTM和ICNN-LSTM模型的预测结果均为82%左右，由此可以看出融合了CNN和LSTM的特点的联合模型在极端峰值处也有较好的拟合情况，具有较好的稳定性。另外，在数据频繁抖动的时间采样点处，ICNN-LSTM模型比CNN-LSTM模型的预测结果更加接近于真实值，这也证实了加入自适应学习率的ICNN-LSTM模型在一定程度上提高了模型的预测精度。

4.3 预测误差分析

为了进一步验证所提模型的性能，使用4种评价指标对误差进行分析，从而比较模型的预测精度：评价值越小，则模型误差越小，模型准确度越高。这4种指标分别是均方根误差(root mean square error，RMSE)、平均绝对值百分比误差(mean absolute percentage error，MAPE)、平均均方误差(mean square error，MSE)和平均绝对误差(mean absolute error，MAE)，其值可通过式(9)～式(12)计算求得。

(9)

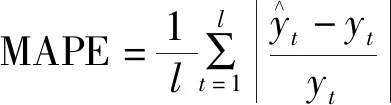
(10)

(11)

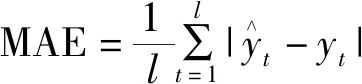
(12)

表1列出了5种模型的模型评价值，通过比较3种不同的模型的模型评价值来去更直接地对比3种模型的预测精度情况，其结果如表1所示。

对于数据量较大的预测情况，LSTM在考虑时间相关性较容易出现梯度爆炸情况。从表1可以看出，拥有较大特征学习能力的CNN和考虑时间相关性的LSTM的表现相差不大，而文献[5]提出的组合模型方法对单一模型的预测精度的提高也是有限的。以均方根误差为例，CNN、LSTM和文献[5]方法的预测误差最优仅为0.934 9，下降了2.63%。CNN-LSTM模型表现较好，预测误差为0.834 9，下降了13.04%。而ICNN-LSTM模型的预测误差仅为0.784 8，下降了18.27%模型的预测精度有了显著提高。

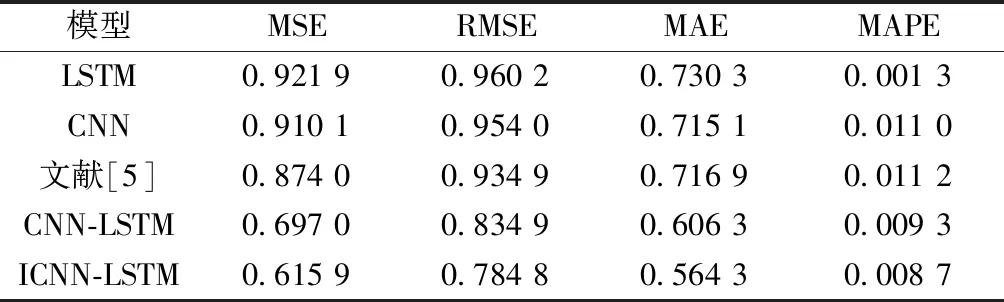
表1 5种模型的模型评价值结果Table 1 Evaluation results of five models

除此之外，对5种模型的训练时间进行对比，其结果如表2所示。

表2 5种模型的训练时间情况Table 2 Training time of five models

从表2可以看出，LSTM模型在考虑时间相关性的情况下花费了大量时间，训练时间较久。同是单一模型，相比LSTM，CNN因其卷积层的特征提取和网络的并行性学习等特点在花费时间上占据较大优势。而联合模型融合CNN和LSTM网络的特点，虽然较CNN模型训练时间有所增长，但是增长量不大，尤其是本文提出的加入自适应学习率的联合模型ICNN-LSTM，在较大幅度提高模型精度的情况下，训练时间也仅多花费0.1 s，可以看出，提出的模型在模型性能方面得到了一定的优化。

5 结论

提出一种基于自适应神经网络的云资源预测模型，可以提前了解未来的资源需求情况，从而做到更及时准确地对云资源进行调度和分配，避免了资源供求不均衡等问题。该模型将CNN和LSTM网络进行联合，让CNN先对数据进行特征激活提取学习后再让LSTM网络进行时序学习，增强了模型的学习效果和预测性能；同时让模型的学习率依据sigmoid函数变化在训练过程中遵循先大后小的特点，从而让模型在不同的学习阶段具有不同的学习能力，提高了模型最终的预测精度。在训练时间仅为25.178 1 s的情况下，所提模型的均方根误差相较于单一模型CNN、LSTM、文献[5]的组合模型和未加入自适应学习率的CNN-LSTM模型分别下降了17.74%、18.27%、16.01%和6%，从而证明所提模型的预测性能有了明显提高，具有实际应用价值。