工业管道内壁损伤重建与检测
2021-09-26张莉华
赵 谦,张莉华,钱 渠
(1.西安科技大学通信与信息工程学院,西安 710054;2.南通智能感知研究院智能遥感事业部,南通 226400)
微细管道广泛应用于石油、能源、化工、医疗、生物等诸多领域[1]。然而,在使用过程中管道受如介质腐蚀、机械震动、高温、高压等因素影响[2-3],会出现结垢、裂纹、剥落和穿孔等损伤,如果损伤过大则会引起事故的发生从而造成重大损失[4-5]。因此对管道内壁的定期检测[1,6]成为管道安全使用的重中之重,由于大多数管道的直径为700 mm或更小,检查员无法直接进入管道进行手动检测。因此,克服空间限制的自动检测方式深受人们推崇,并且人们也在不断地提高实时性、准确性和鲁棒性。当今,管道检测方式包括无损检测[7]和基于机器视觉[8-9]检测。无损检测方式有激光法[10]、超声波[11]、涡流[12]、漏磁通法[13]等,这些检测方式都依赖于信号的反复发送和接收,无法提供任何视觉线索,从而导致检测效率低下。基于机器视觉检测是一种新方法,可避免人工检测的不足。目前已被广泛用于评估管道的状况或质量[14]。张广军等[15]研究了微细管道内表面缺陷,得出由于检测时需对结构光视觉传感器进行现场标定,限制了检测范围,也缺少管道内表面纹理信息,故无法达到对树根、腐蚀、裂缝等缺陷的检测。王颖等[16]提出一种圆结构光视觉检测系统,实现了管道形变、弯曲等缺陷检测。Kannala等[17]运用双曲面镜全景相机获取管壁整个圆周的图像,采用运动恢复结构(structure from motion,SFM)方法检测,但由于特征点提取与匹配问题,所以检测精度不高。Yi等[18]提出用激光和圆柱形透镜实现全方位测量,但效果不佳。为了解决上述研究存在的问题,现基于机器视觉提出基于内窥镜的管道内表面无畸变重建方法,以期实现管道内表面损伤部分的完整呈现,这也是管道损伤检测的重要发展方向。
1 平台搭建与图像采集
基于内窥镜的管道内表面无畸变重建方法流程图如图1所示。
通过搭建微细管道内壁无损检测[19]平台来实现探伤检测。该平台主要由待测管道、可编程逻辑控制器(programmable logic controller,PLC)、步进电机、功率放大电路四部分组成,如图2所示。
在本实验采集平台研究的基础上,将其改进并应用于工业生产实践之中,其结构如图3所示。
该装置结构简单、设计合理、实用性强,传输管道内部影像信息稳定、图像定位准,较好地解决了高温高压环境下的管道检测、误伤检测管道、基于视频的管道内壁展开无畸变等问题。
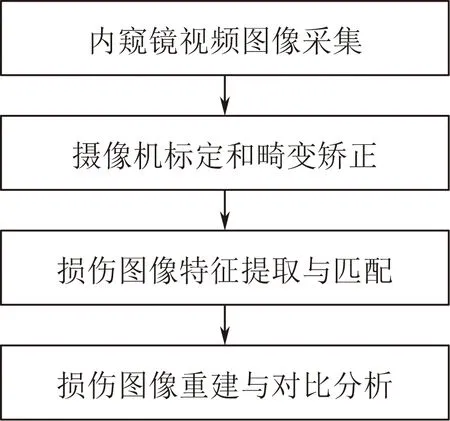
图1 管道内表面重建结构图Fig.1 Reconstruction structure of inner surface of pipeline
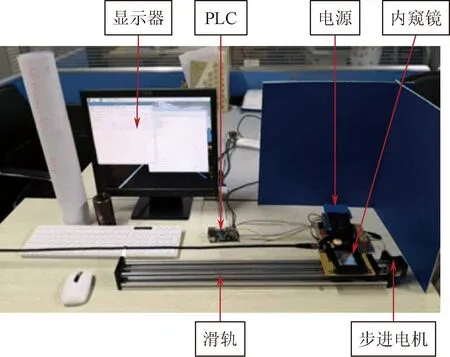
图2 实验平台展示Fig.2 The display of experimental platform
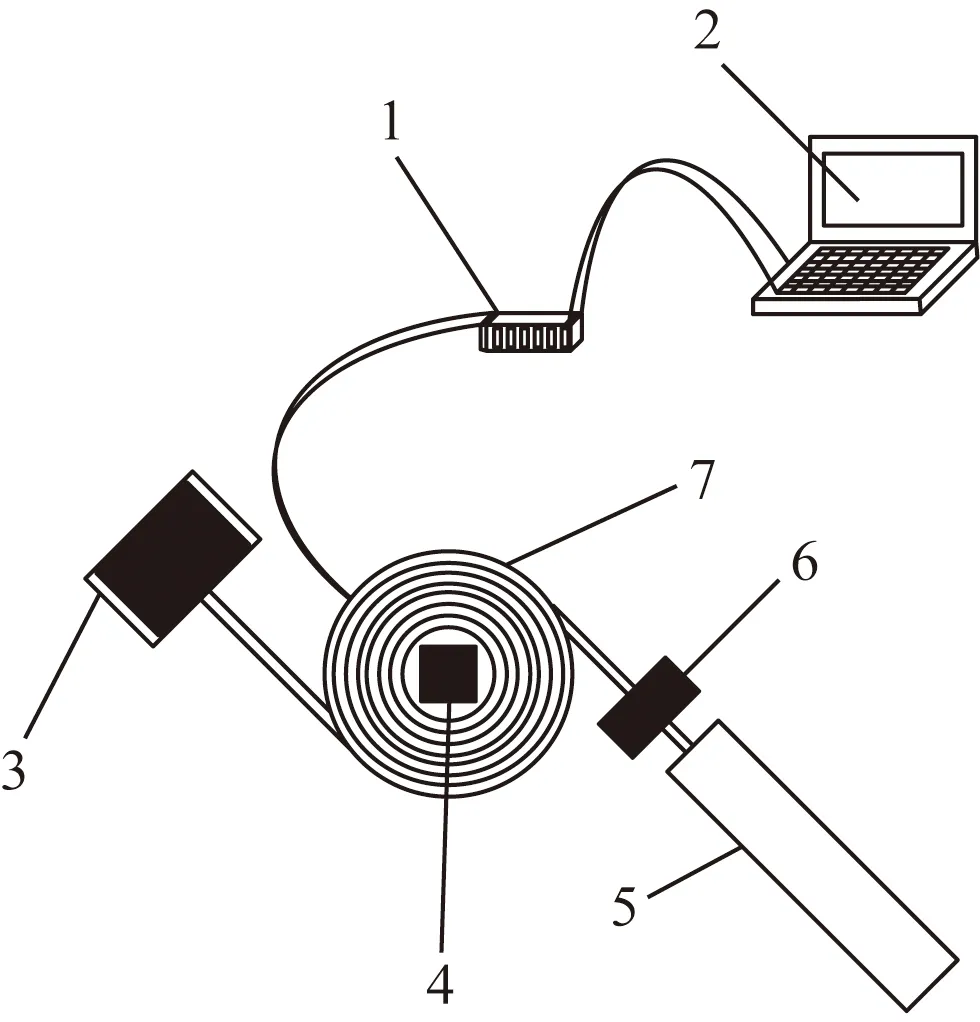
1为驱动器;2为PLC;3为内窥镜显示屏;4为步进电机;5为管道;6为拉直机;7为盘线图3 一种管道内壁探伤装置Fig.3 A flaw detection device for pipe inner wall
待检测管道为某研究院提供的热力管道,是由聚乙烯外护管、聚氨酯和钢管组成,内壁材质为碳钢,内径大小36 mm。内窥镜的有效像素为300万,帧率为12 FPS,最大分辨率为2 048×1 536,利用上述实验平台进行视频采集,将内窥镜置于用步进电机控制的滑轨上,步进电机通过 PLC 控制前进后退,从而对管道内壁空间进行实时扫描,显示器作为用户界面,直流电源为电机提供充足的电量,将采集到的内部视频上传至上位机来对管道内部探伤进行精确定位并提取。
2 摄像机标定与畸变矫正
首先建立管道与工业内窥镜位姿模型,将其等效为针孔相机模型[20-21],如图4所示,为得到内窥镜镜头内参信息,利用张正友标定法[22]来计算内窥镜主点在图像上的位置值。
世界空间中点P与物理成像面上点P′的关系为
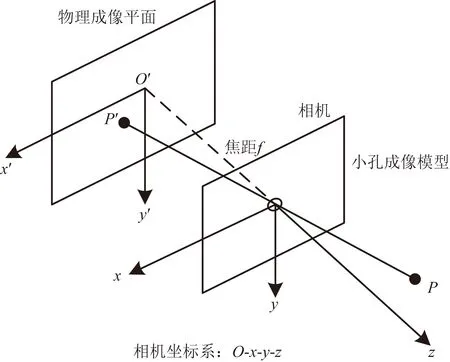
O-x-y-z为相机坐标系;O点为摄像机的光心,即相机模型中的针孔;z轴为相机正对方向;x轴指向右侧;y轴指向下侧图4 针孔相机模型Fig.4 Pinhole camera model
(1)
(2)
为了求取内窥镜镜头的内参信息[23-24],采用10 mm×10 mm的棋盘格标定板,分别从远、近不同视角拍摄角度不同的图像,利用MATLAB中Camera Calibration Toolbox工具箱进行内窥镜的标定,再通过角点检测,先提取每一幅图像中的顶点得到顶点图后,再通过计算得到内窥镜的内参结果。最终得到的内窥镜主点参数为(814,692)。
通过得到的内参信息提取管道圆环并对圆环进行畸变矫正,最后将矫正后圆环全景展开[25],为后续特征提取与拼接做基础。图5为提取到的管道内壁探伤图像,通过内窥镜的相机主点坐标位置提取管道内壁圆环如图6所示。
通过观察上述圆环图像,可从位移和角度两个方面进行畸变矫正,矫正结果如图7所示。
依据得到的管道内壁圆环图像将其展开[26],其步骤大致分为以下两步[27]。
步骤1 切向展开,即以圆形图像中的内外圆半径差作为展开后矩形的宽,外圆周长作为矩形的长,将环形图像展开为矩形图像。

图5 管道探伤图像 Fig.5 Pipe flaw detection image

图7 管道内壁标准圆环图像Fig.7 Standard ring image of pipe inner wall
步骤2 径向展开,提出通过管道内壁与成像面之间的几何关系进行径向拉伸。
原始点p(x,y)经过切向转换后坐标为p′(x′,y′),而期望得到的展开图像对应的坐标为p″(x″,y″),两者之间存在关系为
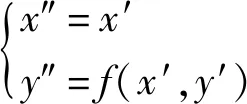
(3)
为了得到坐标,现根据图8确定切向展开表达式为
(4)
展开结果图如图9所示。
将提出的通过管道内壁与成像面之间的几何关系进行径向拉伸算法与文献[25]、文献[26]这两种径向展开方式进行对比。通过展开图像每行的径向间距与实际值之间关系进行对比分析,主要从欧式距离、均方误差以及时效性3个指标来分析,如表1和表2所示。

图8 管道切向展开示意图Fig.8 Schematic diagram of tangential expansion of pipeline

图9 探伤图像全景展开结果图Fig.9 Result of panoramic expansion of flaw detection image

表1 各个算法径向间距对比结果Table 1 Radial spacing comparison results of each algorithm

表2 各个算法指标分析结果Table 2 Analysis results of each algorithm index
由表1得出,展开后探伤图像各行横径向间距和行数间距的均值。通过均值对比,文献[26]和本文算法与实际值之间的差距均小于文献[25],所以文献[26]和本文算法优于文献[25]。文献[26]和本文算法之间的均值差距为0.67,在工业管道内壁的检测中,该差距不足以评判算法的优劣,故通过适用于工业管道内壁的检测的指标进一步阐述。
欧式距离:也称欧几里得距离,用来衡量估计值与实际值之间的绝对距离;距离越小,两数值之间越相似,说明算法性能越好,公式为
(5)
均方误差(mean squared error,MSE):均方误差是指估计值与实际值之差平方的期望值;用MSE评价数据的变化程度,MSE的值越小,说明算法具有更好的精确度,公式为
(6)
式中:t=1,2,…,N为样本的个数;xt为估计值;yt为实际值。
由表2中文献[25]、文献[26]和本文算法的3个指标结果可得:文献[25]的欧式距离、均方误差和时效性均远远大于文献[26]和本文算法,故在恢复为实际图像方面,其效果劣于本文算法和文献[26];虽然本文算法的欧式距离和均方误差略大于文献[26],但本文算法的时效性远高于文献[26],因为文献[26]在径向展开前,需要对管道进行黑白网格点的标定,计算拟合方程的参数值,故复杂程度也较高;结合表1数据,文献[26]的数据具有随机性,而本文算法的数据具有规律性且相对稳定。同时因为工业管道内壁的检测的主旨就是要在保证精度的同时提高时效性,降低复杂度,所以综合可得本文算法可以满足需求。
3 探伤图像拼接
3.1 特征提取
图像特征提取前先进行图像预处理,首先对探伤图像进行形态学重建[28]处理,使重建后的图像的探伤边缘轮廓信息更加清晰,接下来利用指数增强函数方法[29]对探伤图像进行增强处理,使探伤区域与背景区域相区分开,为后续的图像拼接[30-31]步骤排除干扰,图10、图11为原始图像与预处理之后的图像。

图10 原探伤图像与形态学处理结果图Fig.10 Original flaw detection image and morphological processing result
特征提取采用对尺度不变特征转换(scale-invariant feature transform,SIFT)的改进。SIFT算法最早由Lowe[32]于1999年提出,并于2004年得到了更深入的发展和完善[33]。该算法提取的特征点为图像的局部特征,其具有很强的独特性、多量性、高效性和可扩展性,SIFT特征提取具体实施步骤如图12所示。
本文对SIFT算法的空间尺度结构和特征描述符进行改进。
(1)空间尺度结构。由于管道内壁图像数据量大,为提高效率,必须减少金字塔影像的阶数和层数,通过结构相似性(SSIM)和峰值信噪比(PSNR)对其进行评价,最终选择的层数为4层。

图11 原始图像与指数增强图像的对比图Fig.11 Comparison of the original image and the exponentially enhanced image
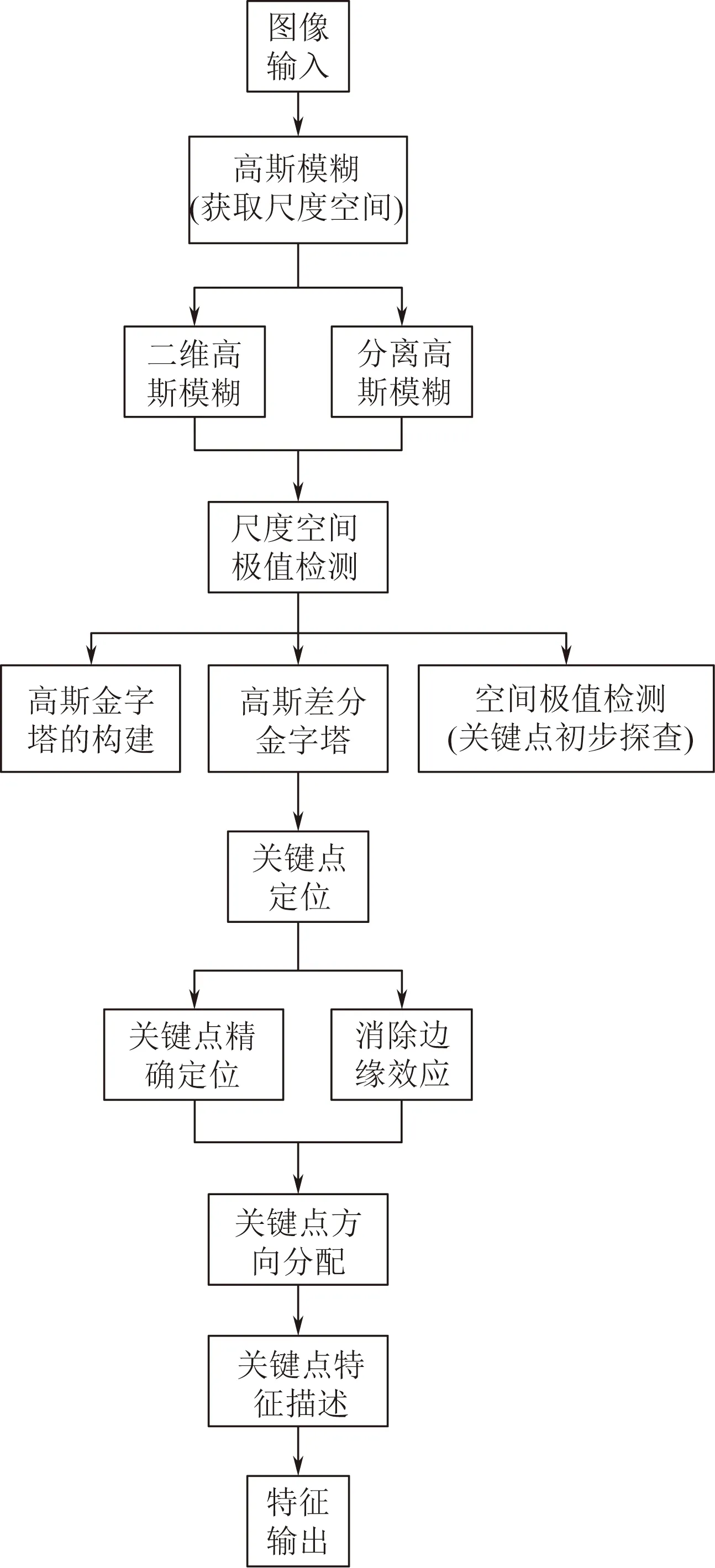
图12 SIFT特征提取过程图Fig.12 The diagram of SIFT feature extraction process
(2)特征描述符。由于高斯函数的轮廓分布为同心圆,相比SIFT中使用的正方形,圆形具有更好的旋转不变性。
因此,选择一个圆形区域作为提取的关键点的局部区域。其大小由描述符[34-37]的计算的关键点的比例来确定。改进后的描述符的圆形区域为一个圆圈和两个圆环,其大大降低了计算复杂度和时间消耗。
由图13可以看出,本文算法提取某探伤图像的特征点数比经典SIFT算法的特征点要多;于是对每幅探伤图像(共14幅图像)进行特征点提取,结果如图14所示。
从图14可以清晰地看出,每幅探伤图像在本文算法下提取的特征点数明显大于经典SIFT算法所提取的特征点数,故本文算法在特征点提取方面优于经典SIFT算法。

图13 管道内壁图像特征点提取结果图Fig.13 Result of extraction of feature points from pipe inner wall image

图14 管道内壁探伤图像特征提取结果对比图Fig.14 Comparison of feature extraction results of pipe inner wall flaw detection image
3.2 图像拼接
3.2.1 特征匹配
首先利用基于特征点相似度[38]进行特征点粗匹配,运用欧式距离对所有的匹配点进行相似度的范围压缩,剔除指定范围外的匹配对即绝大部分为错误匹配对,其主要目的是提纯匹配对,进而缩减算法时间,提高算法时效性,公式为
(7)
式(7)中:i=1,2,…,n为图像个数;xi为匹配图像特征点;yi为被匹配图像特征点。
接下来采用鲁棒性较强的RANSAC算法[39-41]去除误匹配点,从而达到细匹配,RANSAC 算法的详细实现步骤如图15所示。
图16、图17为经典SIFT算法结合随机抽样一致(random sample consensus,RANSAC)算法剔除误匹配与本文算法结合RANSAC算法剔除误匹配后的匹配结果。图18为匹配对对比图。

图15 RANSAC算法流程图Fig.15 The chart of RANSAC algorithm flow
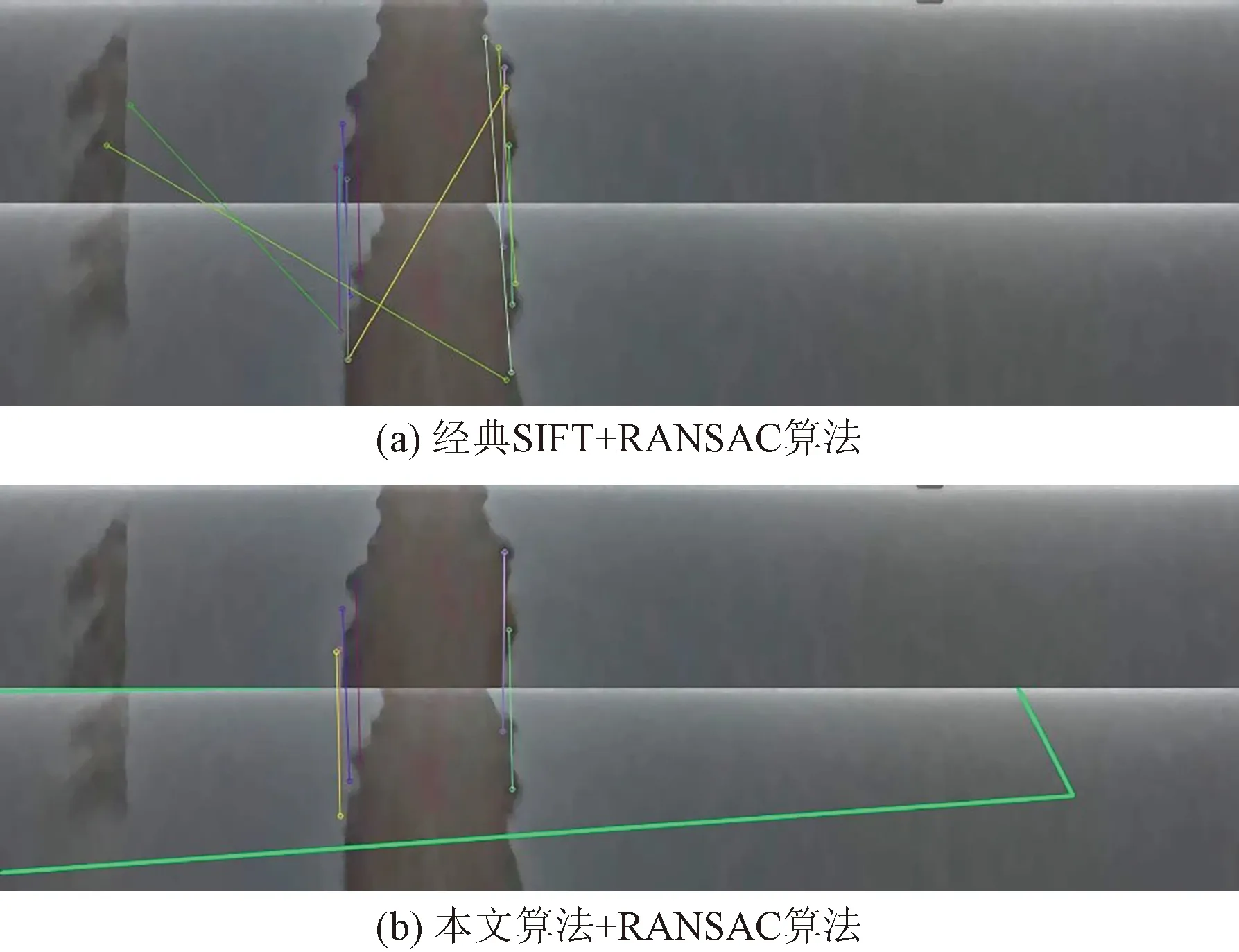
图16 探伤1匹配结果图Fig.16 Matching result of flaw detection 1

图17 探伤2匹配结果图Fig.17 Matching result of flaw detection 2

图18 管道内壁探伤图像匹配对对比图Fig.18 Comparison of matching images of pipe inner wall flaw detection
由图16~图18可知,经典SIFT算法通过RANSAC算法剔除误匹配的特征点匹配结果与本文算法通过RANSAC 提纯后的匹配结果可以看出,本文算法可以剔除大量的误匹配,使匹配结果更加精确。
3.2.2 图像融合
采用像素灰度值加权(渐入渐出)融合算法[42-43]对上述所得的匹配结果图像进行融合,最终实现完整的探伤区域。
该算法实现过程可以表示为
F(m,n)=ω1F1(m,n)+ω2F2(m,n)
(8)
式(8)中:m和n分别为图像像素的行号和列号,m=1,2,…,M,n=1,2,…,N;ω1和ω2分别为第一幅原图和第二幅原图的加权系数;一般情况下,ω1+ω2=1。该算法是在灰度值平均融合算法基础上发展而来的,加权融合算法在实现时引入了权重的概念,能够在某种程度上有效提高融合图像的信噪比。为了使两幅原图平稳过渡且接近无痕,应该选择恰当的权重值,即ω1=ω2=0.5。
图19(a)所示为未经融合的拼接结果,可以发现拼接处存在较为明显的拼接缝。针对这种情况,选用该融合算法对图像进行像素灰度值加权融合处理,结果如图19(b)所示,融合后的图像之间过渡较为平缓,图像间拼接缝明显消失,而且图像信息基本全数保留,达到了预期的效果,同时也为后面的图像分割、探伤统计消除了一定的隐患,避免了不必要统计误差的生成。下面对完整探伤图进行了融合,为了提高主观视觉体验,对拼接后的图像又做了增强处理,如图20(a)和图20(b)所示。

图19 探伤3融合结果图Fig.19 Fusion result of flaw detection 3

图20 完整探伤拼接效果图Fig.20 Complete flaw detection and splicing effect
4 算法结果统计与分析
以图9展开图像为例,又采用了经典SIFT拼接算法、文献[44]算法和文献[45]算法以及文本算法对图像进行了拼接,如图21所示。
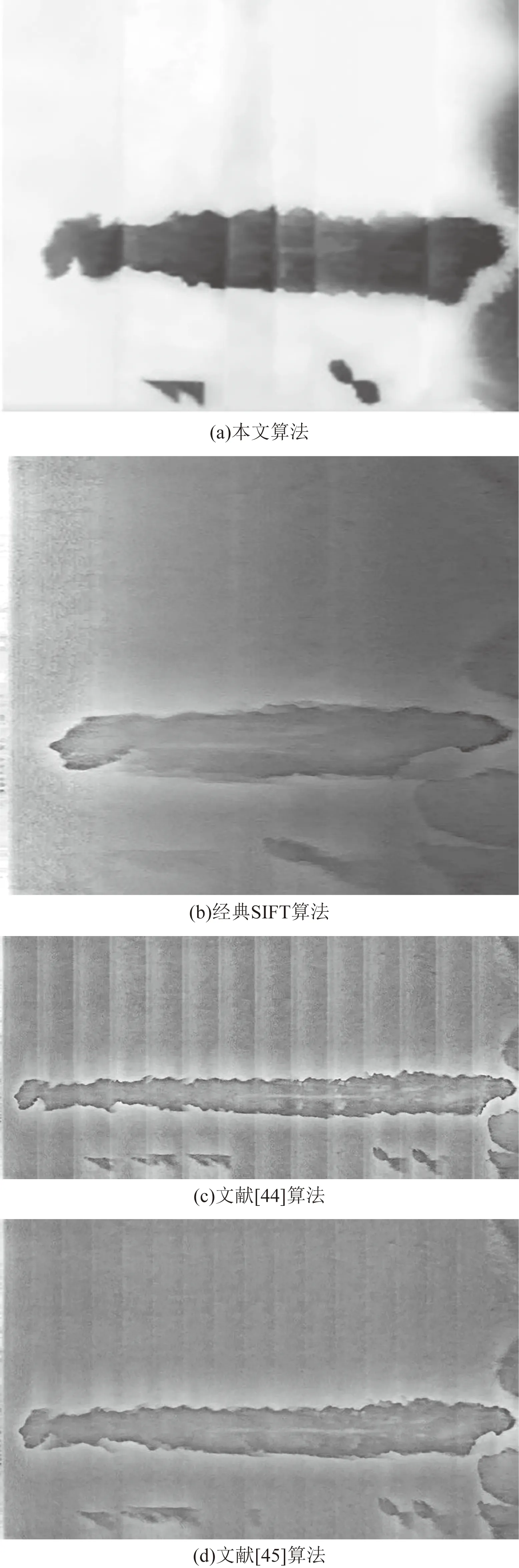
图21 各算法探伤图像拼接的对比结果Fig.21 Comparison results of splicing of flaw detection images by various algorithms
由图21可以看出,在探伤图像的拼接过程中,经典的SIFT算法出现较为明显的鬼影现象,很多不是重叠区域的部分被当作了重叠区域来拼接,造成了过度拼接,而且由于重叠区域过多导致图像亮度明显降低;文献[44]拼接结果没有完全去除重叠区域,尽管边界相对光滑,但有明显的拼接缝存在;文献[45]拼接结果尽管消除了拼接缝问题,但没能完全去除重叠区域;本文算法即消除了拼接缝和鬼影现象,还提高了主观视觉的体验,图22为阈值分割后完整探伤重建结果。

图22 完整探伤重建结果二值图Fig.22 Binary figure of complete flaw detection reconstruction results
为更形象地说明算法的优势,采用了时效性和准确率来分析拼接结果。准确率是由探伤面积体现,公式为
(9)
式(9)中:t为拼接的准确率;S1为原始探伤图的面积;S2为算法拼接结果探伤面积。
由于热工院提供管道探伤原始面积无法获取,于是本文模拟了管道内壁探伤对图像拼接算法进行了验证,如表3所示,模拟的管道原探伤面积为11.491 cm2。
由表3各个算法的时效性和准确率拼接结果可以看出,文献[45]的时效性最高,但其准确率却是最低;文献[44]的时效性和准确率都不是最优,这说明管道内壁图像的拼接不能用块匹配方法,这种算法会使误差很大;相比较经典SIFT算法,本文算法的改进达到了预期效果,在时效性和准确率方面都有提高。因此,本文算法对SIFT算法的改进可以达到工业管道内壁检测需求。
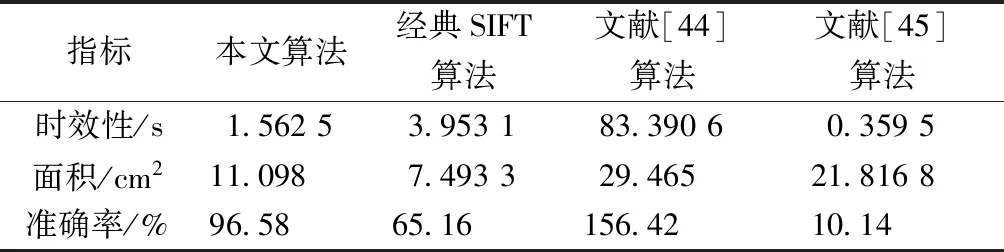
表3 各算法拼接结果对比Table 3 Comparison of stitching results of various algorithms
5 结论
微细管道内壁的无畸变重建,通过搭建工业管道内壁检测平台,获取探伤每帧图像并对图像进行矫正和展开,接着对探伤展开图像进行形态学增强与指数增强,增强探伤边缘轮廓信息与区分背景与目标,然后对探伤图像进行拼接融合,最后通过计算拼接后图像面积的准确率为是否需要管道检修提供依据。
实验中,将本文算法与经典SIFT算法、文献[44]算法和文献[45]算法的拼接结果进行了对比,本文算法的时效性达到了1.562 5 s,准确率达到了96%以上,通过比较可以得出,本文算法在时效性和准确率方面都更加优越,且其鲁棒性也较好,可以达到工业管道检测需求。
