某型扫雷辊在爆炸环境下的仿真与试验研究

沙康康，王显会*，郭 峤，彭 兵，孙晓旺

(1.南京理工大学机械工程学院，南京 210094;2.重庆长安工业(集团)有限责任公司，重庆 401120)

地雷作为一种有效的杀伤和破坏武器，是人类使用的最古老的热兵器之一，即使是在现代战争中仍被广泛用于约束地面武力移动、防护特定地区等方面。随着地雷的多样化、系列化以及各类大面积、快速机动布雷设备的问世，战争中地雷就成了装甲部队实施机动的一大障碍。

在地雷的爆炸冲击下，车身自身结构会发生严重变形，同时爆炸产生的冲击波会对乘员造成伤害，为此增强装甲车辆自身的抗爆性能及研制各类扫雷装置显得尤为重要。随着有限元技术的发展，已经广泛应用于模拟爆炸及研究乘员防护的数值仿真中。王世达等[1]采用有限元分析方法，研究了某型军用车辆在斜坡滚翻过程中驾驶员及副驾驶员的运动姿态，确定了乘员损伤评价指标；孙晓旺等[2]建立了某车辆在爆炸冲击下底部防护组件的有限元模型，并通过爆炸冲击台架试验验证了有限元模拟的可靠性;胡建宇等[3]建立了某军用装甲车辆的有限元模型并进行了爆炸仿真分析，研究了不同梁结构对车辆防护性能的影响；熊鹏宇等[4]通过有限元模型对试验进行验证和优化，提升了某型军用车辆在底部爆炸环境下座椅的防护性能。与试验方法相比，采用有限元仿真分析可以减少大量试验准备工作，为研发团队节省大量的时间和资金。此外，在中国还没有公开关于扫雷车在爆炸环境下损伤情况的相关研究。

现以某型扫雷车前挂扫雷辊为研究对象，通过几何清理、网格划分等方式建立扫雷辊系统有限元模型，同时建立炸药、空气及土壤的流场模型，整合构建爆炸冲击动力学仿真模型，利用任意拉格朗日-欧拉(arbitrary Lagrange-Euler，ALE)算法对8 kg 三硝基甲苯(tri-nitro-toluene，TNT)地雷替代物爆炸环境下扫雷辊结构的损坏情况进行仿真分析，研究扫雷辊的损伤情况。随后进行扫雷辊的实爆测试，研究8 kg TNT地雷替代物爆炸环境下扫雷辊结构的损坏情况，并将试验和仿真结果进行对比，验证模型的准确性。

1 有限元模型的建立及仿真条件

1.1 仿真算法的选择

在连续介质力学[5]中，有两种经典的运动描述方法，一种是Lagrange描述，另一种是Euler描述，在描述有限元运动界面时也采用这两种方法。Lagrange描述中，网格节点固定在物质点上并随之运动，因此在描述运动边界或者运动界面时非常方便，但是当物质发生大变形时常常使网格发生畸变，影响单元的近似精度甚至会使得计算终止；Euler描述中，网格节点固定在空间始终不动，因此在大变形时网格不会发生畸变，但是其无法精确确定运动边界或者运动界面的位置。

ALE算法[6-9]的计算网格则不再固定，也不依附于流体质点，而是可以相对于坐标系做任意运动。利用拉格朗日网格对不可压缩的材料结构进行划分，而可压缩的流体材料(如空气，水)则用欧拉网格划分[10]。这结合了拉格朗日算法与欧拉算法的优点，既避免了网格发生大变形出现畸变的问题，也解决了空间网格不移动的缺点，能够有效地模拟流体与固体的耦合问题，利用ALE描述物质物理量的表达式为

(1)

式(1)中：f为物质点物理参数；vi为物质i质点的速度；wi为参考点ξ的速度。当参考点速度wi为0时，空间网格固定不动，材料网格运动，即模型整体呈现欧拉网格的特点；当参考点速度wi等于物质的流速vi时，空间网格与材料网格不存在相对运动，即呈现为拉格朗日网格的特性；当参考点速度与流体速度不相等时，空间网格与材料网格可以一起运动，并且材料网格可以在空间网格一定区域内流动。因此，ALE算法能有效模拟泥土、空气和冲击波的整个流动过程，计算精度高、可靠性好，是目前最有效的仿真算法[11]。

采用ALE流固耦合的算法对扫雷辊进行仿真分析，其中扫雷辊结构采用Lagrange网格，空气、土壤和炸药采用Euler网格，研究扫雷辊结构在8 kg TNT炸药爆炸冲击下的损伤情况。

1.2 扫雷辊结构有限元建模

在进行扫雷辊结构的有限元网格划分前，要对具体结构的三维数模进行简化，并对复杂零部件进行必要的几何清理，避免划分出来的部分不规整单元以及一些尺寸过小的单元会造成求解计算时间步长过小，增加计算机求解时长[12]。

扫雷辊系统有限元模型主要由扫雷辊轮、转向机构、伸臂和连接架4个部分组成，如图1所示。由于模型大部分为钣金件，其厚度比长和宽小得多，因此用壳单元进行网格离散划分，网格类型主要为四边形单元和三角形单元，其中三角形单元所占比重小于5%，而轮胎、前横梁及连杆等不易提取中面的部件则采用体网格进行划分，网格单元尺寸均控制在8～10 mm。网格划分从形状较小且复杂的曲面开始，每划分一个零部件都要检查网格质量，检查的项目包括：最小边(>5 mm)、翘曲度(<15°)、最大/最小角度(45°～135°)、单元的雅可比(>0.65)等[13]，避免单排网格或单边连接网格并调整直至满足条件。最后将所有的零部件网格合并，调整位置错误的零部件，检查及避免零部件出现初始穿透和干涉的现象。建立的扫雷辊系统有限元模型如图2所示，共划分单元数量404 183，节点数量487 162。

为了准确模拟零部件之间的相对运动，需要根据扫雷辊实际模型建立准确地连接关系。由于扫雷辊结构大部分都是由钣金件焊接而成，所以要考虑连接部位的焊接失效问题，各部件之间的焊接关系以Beam单元模拟焊点，部分部件距离炸点位置较远，暂不考虑焊接失效，以Rigidbody单元进行刚性连接；螺栓孔部位不考虑螺栓紧固件的失效问题，因此也用Rigidbody单元模拟连接。为了防止部件在爆炸冲击的作用下发生大变形与周围其他部件发生穿透，保证爆炸冲击力的传递，扫雷辊各部件之间采用关键字*CONTACT_AUTOMATIC_SINGLE_SURFACE设置自接触。

1.3 扫雷辊材料参数设定

扫雷辊系统主体结构材料采用Q345，销轴部分材料选用45号钢，均采用*MAT_PLASTIC_KINEMATIC材料本构模型，具体的材料参数如表1所示。轮胎部分为橡胶材料,选用*MAT_OGDEN_ RUBBER材料本构模型，其材料参数如表2所示。

表2 橡胶材料参数Table 2 Material parameters of rubber

1.4 爆炸流场及爆炸边界的建立

图3为爆炸流场的有限元模型。土壤网格模型长×宽×高为3 510 mm×2 000 mm×600 mm的立方体(图中绿色部分)，网格尺寸为30 mm，单元总数为275 000，其上表面与空气网格的下表面采用共节点的方式实现连接。建立的空气网格模型长×宽×高为3 510 mm×2 000 mm×1 200 mm的立方体(图3中蓝色部分)，能够容纳整个扫雷辊系统和连接结构，单元尺寸为约30 mm的六面体实体单元，单元总数为181 500，其材料采用空的材料模型并使用线性多项式状态方程，表达式为

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(2)

式(2)中：p为气体压力；C0～C6为多项式方程系数，分别取C0=-0.1，C1=C2=C3=C6=0，C4=C5=0.4；E为空气单位体积内能，取0.253 3 mJ/mm3;μ=ρ/ρ0-1,ρ0为初始密度，空气密度ρ=1.293 kg/m3。

TNT炸药为圆柱形，当量为8 kg，放置在扫雷辊单侧中心位置的正下方(右侧三轮正下方)，炸药上表面距离土壤表面100 mm，炸药位置示意图如图4所示，图中也对扫雷辊轮进行了编号。

采用关键字*INITIAL_VOLUME_FRACTION_GEOMETRY对炸药的初始体积进行定义，炸药密度ρ=1.63×103kg/m3，爆炸速度D=6 930 m/s，爆炸压力PCJ=21 GPa。爆炸产物气体采用Jones-Wilkins-Lee(JWL)状态方程，即

(3)

式(3)中：A、B、R1、R2、ω为材料常数；V为相对体积；E为炸药单位体积的内能，状态方程参数如表3所示。

图3 爆炸流场有限元模型Fig.3 Finite element model of explosion flow field

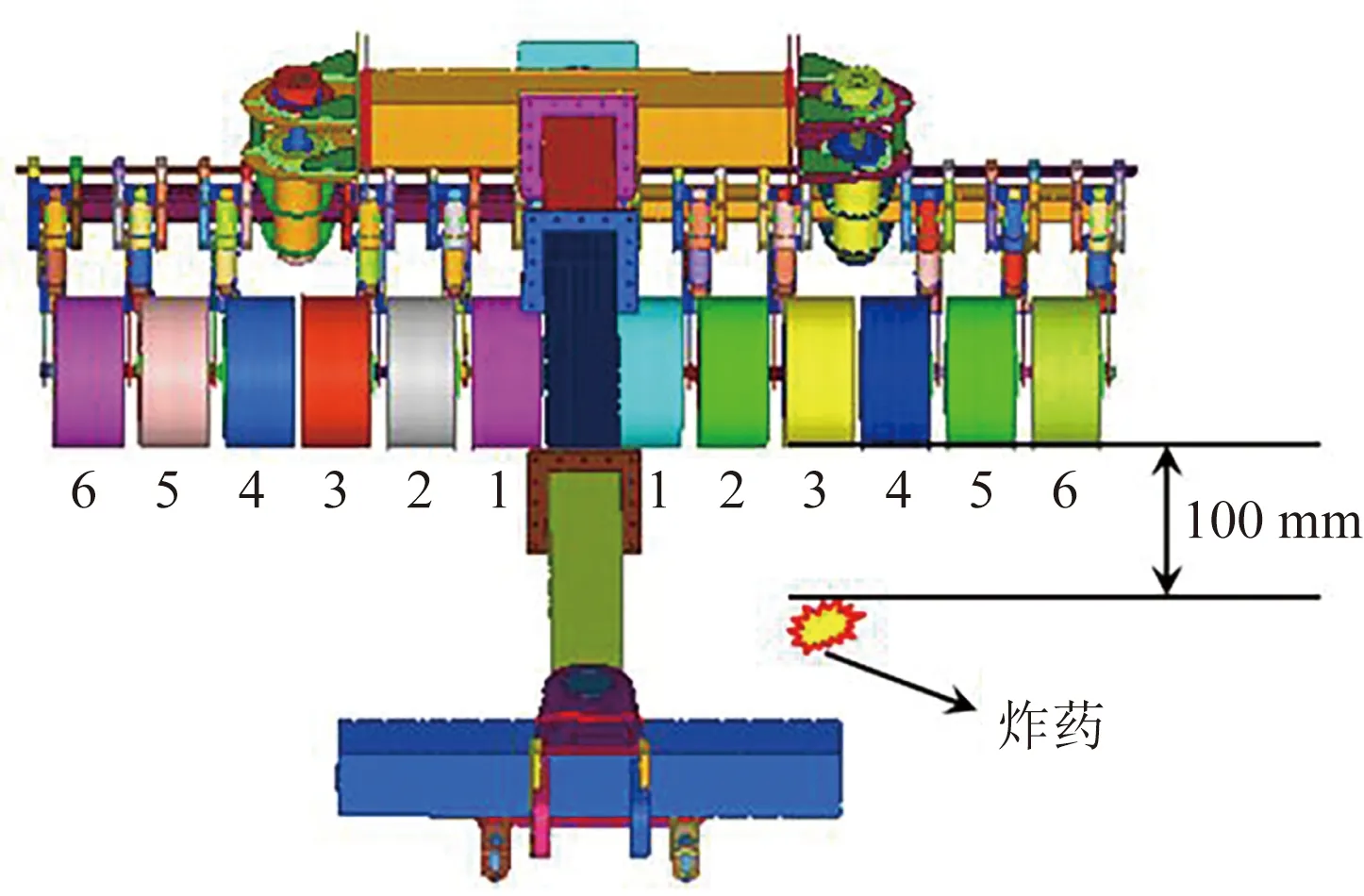
图4 炸点位置示意图Fig.4 Schematic diagram of explosion point location

表3 TNT炸药状态方程参数Table 3 TNT explosive equation of state parameter

土壤、空气、炸药和扫雷辊结构之间涉及流体与固体的耦合作用，使用关键字*CONSTR-ANED_LAGRANGE_IN_SOLID来处理多物质流固耦合问题，分布在每个拉格朗日表面片段上积分点为2、采用壳单元和实体单元的惩罚函数耦合法，耦合方法采用法向压缩、罚函数刚度缩放因子设置为0.15，泄露控制惩罚因子设置为0.1。

2 数值仿真计算结果分析

8 kg TNT当量炸药爆炸冲击下扫雷辊结构的损伤随时间的变化情况如图5所示。从整体的损伤结果上来看，扫雷辊的右侧结构受损严重，扫雷辊轮基本全数脱落飞出，轮毂与轮胎分离，减震器遭到严重破坏，连接横梁由于应力集中而发生断裂；而扫雷辊左侧结构几乎没有受到爆炸冲击的影响，整体结构基本保持完整，只有靠近左侧炸点侧的一号轮胎的摆臂发生了轻微的塑性变形；伸臂结构在爆炸冲击下没有发生明显的塑性变形。

由图5的结果可以看出，爆炸冲击波首先与炸药正上方的轮胎发生耦合作用，轮胎发生明显扭曲变形，爆炸冲击力传递到轮毂处，在强冲击力作用下，炸点上方轮毂发生较大的变形和破坏。图6为爆炸发生后1 ms轮毂应力分布情况，最大应力达到569 MPa，单元达到失效条件删除，轮毂开始发生损坏。随着轮毂受冲击力发生的向上运动，减震器结构受到压缩，在强冲击力作用下减震器臂筒受挤压破坏。在爆炸冲击力持续作用下，轮毂与摆臂连接处发生断裂，轮胎飞离，轮毂与轮胎也发生脱离，如图7所示。最后，爆炸冲击力到达轮胎连接横梁，横梁开始发生变形。随着爆炸场的持续扩大，横梁受到更大的爆炸冲击力发生严重的塑性变形，在爆炸发生后52 ms左右断裂，如图8所示。

图5 扫雷辊结构在爆炸冲击作用下损伤情况主视图Fig.5 Main view of damage of minesweeper roll structure under explosion impact

通过对仿真结果的分析，右侧扫雷辊结构(炸点侧)变形破坏严重，轮毂受冲击脱离飞出，轮胎连接横梁断裂，然而爆炸冲击波快速衰减未对左侧结构造成大的破坏，只有左侧靠近炸点位置轮胎摆臂发生了塑性变形，但是总体结构保持完整，扫雷辊结构连接臂保持完好，仅发生了倾斜，如图9所示。

图6 炸点上方轮毂应力分布情况Fig.6 Stress distribution of the hub above the blast point

图7 轮胎与轮毂发生脱离Fig.7 The tire disengages from the hub

图8 轮胎连接横梁发生断裂Fig.8 The tyre connection beam has broken

图9 计算结束后连接臂状态Fig.9 The state of the connecting arm after the calculation is finished

3 爆炸性能测试试验及结果分析

为了验证8 kg TNT当量地雷替代物爆炸冲击下扫雷辊结构的破坏情况以及数值仿真模型的准确性，参考AEP-55 VOL(2)[14]的试验方法对扫雷辊进行了实爆测试。

3.1 试验设计

试验样车配置及状态保证可正常行驶功能，扫雷辊与车辆按实际状态连接，同时，按照实车战斗全重进行配重，如图10(a)所示。

试验所用TNT质量为8.1 kg，高径比H/D为1/3，密度为1.58 g/cm3，尺寸为8.9 cm×Φ27.1 cm，爆炸品实物图如图10(b)所示。试验前，按照AEP-55 Vol(2)中对爆炸品掩埋场地的要求准备专用的起爆沙坑。在硬质土壤的场地挖出长×宽×高规格为2 m×2 m×1.5 m的方坑，坑内完全填埋符合标准规定的砂石。试验样车按照正常使用状态停放在预先设置好的试验场地指定位置，地雷替代物埋设在扫雷辊右侧3轮下100 mm处。

图10 试验前准备Fig.10 Pre-test preparation

3.2 试验结果分析

爆炸试验后扫雷辊整体损伤情况如图11(a)所示，扫雷辊右侧的轮胎在爆炸冲击作用下全部飞出，轮胎连接横梁发生断裂与整体结构分离，而非炸点侧即扫雷辊左侧结构没有受到爆炸冲击的影响发生严重变形损坏，只有靠近右侧的轮胎发生了些许的塑性变形，爆炸冲击对扫雷辊主体结构的影响不大，结构基本保持完整，与图5所示的仿真结果保持一致。

图11 爆炸试验后扫雷辊的损伤情况图Fig.11 Damage diagram of minesweeper roll after explosion test

图11(b)为扫雷辊右侧结构在爆炸冲击作用下飞出的轮胎，此轮胎为5号轮胎，即非炸点正上的轮胎，其轮胎结构没有发生损坏，因为减震器顶端与轮胎连接横梁发生断裂而整体飞出；图11(c)为飞出的右侧结构3号轮胎轮毂，其是在炸点正上方的轮胎，受到的爆炸冲击的影响最大，因此轮胎在轮胎飞出后，自身结构也严重损坏；试验后连接臂状态如图11(d)所示，连接臂没有发生明显的变形，其与车身的连接位置发生断裂并脱离车身，上述试验现象与有限元仿真现象均吻合。

综上，扫雷辊右侧结构(炸点位置)损伤严重，轮胎、轮毂、支撑臂等部件脱离扫雷辊主体，轮胎连接横梁断裂，与扫雷辊的转向机构分离；扫雷辊左侧结构(非炸点位置)基本保持完好，连接臂无明显损伤。将上述试验结果与上一节中的数值仿真结果进行对比，仿真中扫雷辊的整体结构与局部变形结构与试验结构基本吻合。

通过在8 kg TNT当量地雷替代物爆炸冲击下扫雷辊结构破坏情况的数值模拟与试验结果的对比，验证了数值模型的准确有效。

4 结论

建立了某型扫雷辊结构的有限元模型，采用ALE算法对8 kg TNT爆炸冲击作用下扫雷辊结构响应进行了仿真分析，研究了扫雷辊结构在爆炸环境下的损伤情况，并且设计和进行了该型扫雷辊结构在8 kg TNT爆炸环境下的实爆测试试验，得出的结论如下。

(1)扫雷辊系统在爆炸冲击的作用下，炸点一侧结构变形破坏严重，而非炸点侧结构基本保持完整，扫雷辊的主体结构没有发生明显损坏。

(2)将扫雷辊系统在爆炸仿真中的毁伤情况与实爆测试试验的结果进行对比分析，扫雷辊结构的损坏形态基本吻合，验证了有限元方法的有效性，且有限元模型精度较高，可用于后续结构的改进和优化工作。