货运车队悬架超轴距车联预瞄控制系统
2021-09-26袁策柳江赵健李明星
袁策, 柳江, 赵健, 李明星
(青岛理工大学 机械与汽车工程学院, 山东 青岛 266520)
近年来,车联网(internet of vehicles,IoV)的研究引起了国内外众多学者的广泛关注,尤其是车联网在货运车队工程运输方面的应用.悬架系统作为车辆的重要组成部分,对改善运输过程中的平顺性、操纵稳定性和安全性起到关键作用.车联网由于具有庞大的网络规模、可靠的互联网连接、与个人设备的兼容性及较高的处理能力等特性,在运输系统中占据了主导地位[1-3].重型货车可以提供有效的货运方式,在国家经济中发挥着重要的作用[4].对于货运车队的货车作业而言,在车队的实际工程运输中,由于运输路线较长,货车数量较多,数据交互量极大,从而导致交互效率降低,成本提高.将车联技术应用于货运车队是运输业关注的热点[5-6].
为了使货运车队尽可能提高悬架的控制效率,学者将预瞄控制方法引入车队货车的运输中,试图在长轴距货车上实施全局车辆控制策略.Sharp等[7]针对单车的紧急制动,应用线性最优预瞄控制理论建立线性化的小扰动模型,根据车速进行线性插值,通过仿真使其达到很好的控制效果,并将该理论应用于一个简单的非线性重型汽车模型中.Krtolica等[8]在主动悬架预瞄控制的基础上,通过预瞄前方道路的轮廓信息,提出一种新型控制算法,可改善乘坐舒适性[9].对车队整体作业而言,庞大的信息量会影响轴距预瞄的控制效果,因此,研究的重要思路是将轴距预瞄控制算法有效地应用于车队悬架中,并结合车联技术,优化系统构架,减少数据交互量,从而保证车队高效地完成作业.基于此,本文提出一种货运车队悬架超轴距车联预瞄控制系统.
1 超轴距车联预瞄的控制方案
车辆间距远大于货车的轴距,称为超轴距.为了减少安全隐患,提高经济效益,车队货车运输具有典型的重复性特征,即相同车型、固定线路完成相同作业,这是超轴距预瞄的前提之一.超轴距车联预瞄方法(简称超轴距预瞄)的基本原理是前车的路面输入及悬架响应类比于轴距预瞄的前轴数据,通过Wi-Fi或其他无线传输方法传递给后续车辆,而后续车辆类比于后轴进行相应的悬架控制.与传统车间互联形式不同,超轴距车联预瞄方法采用两车之间优先结对,而对与对之间再采用车间互联的形式,从而降低近一半的数据交互量.
超轴距预瞄示意图,如图1所示.图1中:A车与B车两两结对,A车采用和C车相同的轴距预瞄,将前轴的悬架控制参数传递给后轴,实现对悬架控制参数的控制;A车与B车之间采用超轴距预瞄,将A车后轴的悬架控制参数传递给B车的前轴.考虑到增加的轴距远小于车间的超轴距,故B车的后轴与前轴直接采用相同的悬架控制参数,B车的悬架控制参数继续向后传递并进行寻优.
超轴距悬架控制的车联网数据交互系统,如图2所示.以联网货车为载体,采集、筛选监测到的路况信息,实现对车队运输道路信息的高效利用.由于结对车辆及对间车辆的数据通讯方式采用Wi-Fi或蓝牙模式,通讯有效距离较短[10],当交互车辆之间的距离大于200 m时,需利用基站进行转接,因此,需要建立车队地理信息监测系统.

图1 超轴距预瞄示意图 图2 车联网数据交互系统 Fig.1 Schematic diagram of super wheelbase preview Fig.2 Data interaction system of IoV
车联网数据交互系统采用GPS和无线通信技术建立GPS监控中心,对车队货车进行准确的定位.前3辆货车的地理位置信息,如图3所示.在电子地图中,车队前3辆货车经过的某一路段,后车获取前车的地理位置坐标,通过传输控制协议/网际协议(TCP/IP)进行通讯,当交通流路况发生变化时,前车向后车发起一个建立连接的同步(SYN)请求,后车主机收到请求后,向前车主机回复一个同步/确认(SYN/ACK)应答,前车主机收到应答后,再向后车主机发送ACK.此时,TCP连接成功建立,前车将地理位置坐标、悬架控制参数、控制状态载入数据包发送给后车,前、后货车建立TCP连接,并进行数据包传输,同时,车队还与云端服务器建立TCP连接,实时更新数据包(图4).GPS监控中心通过云端服务器分析和处理车辆数据信息,计算车队货车的最优悬架参数,及时发送给后面跟随的货车,实现对货车、道路的智能监控、调度和管理.
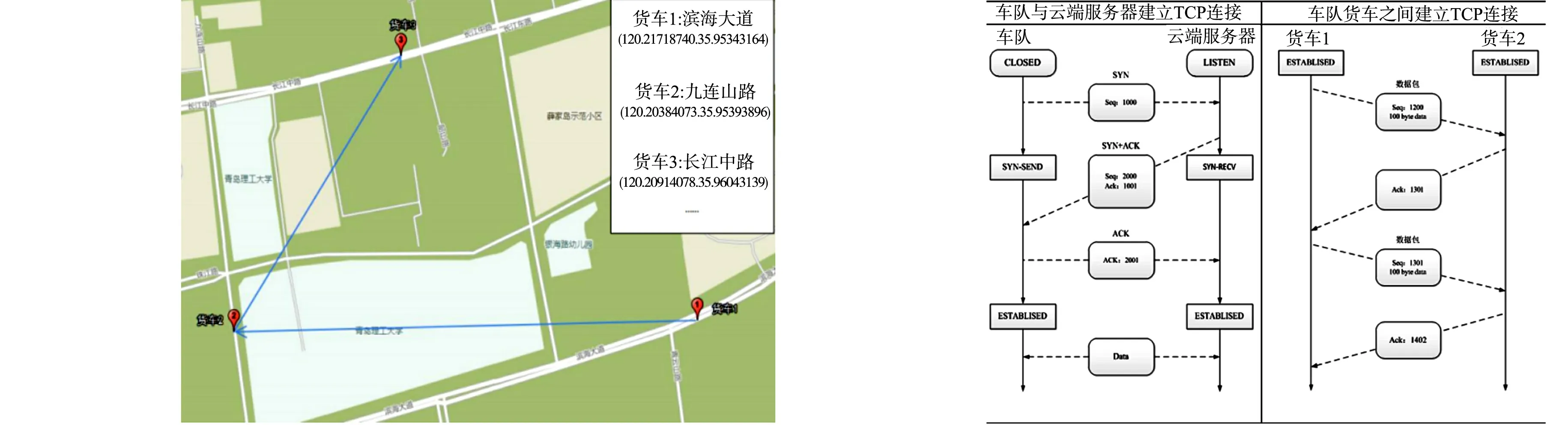
图3 前3辆货车的地理位置信息 图4 TCP连接的建立 Fig.3 Geographic location information of first three trucks Fig.4 Establishment of TCP connection
2 轴距预瞄的优化设计
对轴距预瞄进行优化设计,由于基于车联网的超轴距预瞄必须先确定最优车距,故采用粒子群优化算法对前、后两车的车距进行优化.
2.1 基于粒子群优化算法的车距优化
粒子群优化(PSO)算法起源于对鸟类捕食行为的研究[11],假设在一个N维的搜索空间,种群由M个粒子构成,第i个粒子的速度Vi和位置Xi分别为
(1)
在每次迭代过程中,粒子速度与位置的更新公式为
(2)
式(2)中:k为当前迭代次数;i=[1,M];j=[1,N];ω为惯性因子;rand1,rand2为[0,1]的随机数;c1,c2为学习因子;pi,j,pg,j均为更新后粒子的位置.
建立车队第λ辆和第λ+1辆货车结对,货运车队所有货车在t时刻的速度集合为v(t),加速度集合为a(t),有
v(t)={v1,v2,…,vλ},
(3)
a(t)={a1,a2,…,aλ}.
(4)
采用文献[12]提出的安全距离为最优车距Sm,n,有
(5)
式(5)中:S0为静态安全距离;tn为车头时距;vm(t),vn(t)分别为前、后两辆结对货车在t时刻的速度;aint,m,bint,m分别为第m辆车的期望加速度和期望减速度.
文中仅考虑驾驶适应性[13],建立车队第λ辆和第λ+1辆货车结对时的目标函数,有
(6)
式(6)中:T为货车在整段道路上的通行时间;Δt为0.5 s;aλ(t)为第λ辆车在t时刻的加速度;aλ,a(t)为第λ辆车在t时刻的期望加速度;aλ+1(t)为第λ+1辆车在t时刻的加速度;a(λ+1),a(t)为第λ+1辆车在t时刻的期望加速度;L为驾驶风格系数;Rλ,(λ+1)(t)为t时刻两辆货车实际距离与最佳距离之差;vλ(t),vλ+1(t)分别为第λ和λ+1辆车在t时刻的速度;Sλ(t),Sλ+1(t)分别为t时刻前、后两辆货车的位置;Sλ,(λ+1)(t)为t时刻的最优车距;S(t)为前、后两车距离的函数,有
S(t)=α·exp(-β(Sλ+1(t)-Sλ(t)-S0))
.
(7)
式(7)中:α,β均为距离函数的当量系数.
因此,基于车用无线通信技术,对车队成对的货车建立约束方程,有
(8)
货运车队在进行作业时,行车距离随着路况信息的变化而变化,由算法性能可知,惯性因子ω对获得最优车距具有关键作用,较大的ω值可以提高全局的搜索能力,较小的ω值有利于算法的收敛.合理设置参数值对优化结果具有积极的意义.
采用惯性因子递减的策略对ω进行优化,以获得最佳车距.根据迭代次数调整ω,有
(9)
式(9)中:ωmax,ωmin分别为惯性因子的最大值和最小值;l,lmax分别为比例系数和比例系数的最大值.
考虑到算法的运算能力和运算速度,采用局部优化方法,令运行步长TA=5 s,每5 s调用一次PSO算法,求出5 s内车队所有货车的加速度,而货车速度可以根据运动学关系得到.
若c1,c2较大,粒子会过早地收敛于局部最优[14];若c1,c2都为零,则粒子的速度为常数,从而导致搜索失败.若M较小,算法收敛速度较快,但容易陷入局部最优;若M较大,算法的优化能力较强,但收敛速度慢.因此,定义M,N,c1,c2等参数,随机生成各粒子的初始位置和速度.算法有以下6个步骤.
步骤1初始化种群,取M=30,c1=0.5,c2=1.因为TA=5 s,取前3队货车进行优化,故N=60.
步骤2计算各粒子的适应度,以此为评价标准.对各约束建立相应的函数,安全距离约束项为
(10)
式(10)中:Dλ,s为第λ辆车安全距离适应度;σs为安全距离系数;Ds为6辆车的安全距离适应度.
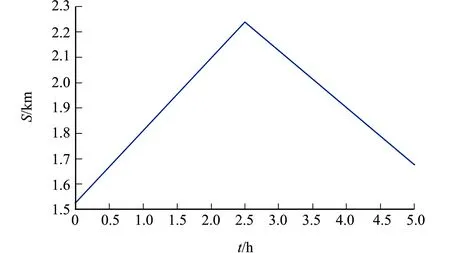
图5 最优车距的仿真结果Fig.5 Simulation results of optimal distance
步骤3求出个体最优值和全局最优值.
步骤4根据式(9)计算ω.
步骤5根据式(1),(2)更新粒子的速度、位置.
步骤6若达到迭代终止的条件,则停止;否则,返回步骤2.
通过Matlab软件进行最优车距的仿真,结果如图5所示.图5中:S为前后两车的车距.
车队的前两辆货车发车时受路况、天气、交通流的影响,车距也随之发生变化.由图5可知:通过粒子群优化算法建立安全距离约束模型,当车距S为2.27 km时,可达到最优解.

图6 超轴距预瞄的主动悬架模型 Fig.6 Active suspension model with super wheelbase preview
2.2 超轴距预瞄系统模型
以解放J6型载重货车为研究对象,满载时,设货车承受载荷为F,货车前轴承受载荷为Ff,货车后轴承受载荷为Fr,簧载总质量为mt.超轴距预瞄的主动悬架模型,如图6所示.图6中:O为质心点;Sa为前车到质心点的距离;Sb为后车到质心点的距离;Z01,Z02均为路面输入;Z1,Z2均为前车后轮的垂直位移;Z3,Z4均为后车前轮的垂直位移;Kt,r为前车的后轮刚度系数;Ks,r为前车的后悬架刚度系数;Kt,f为后车的前轮刚度系数;Ks,f为后车的前悬架刚度系数;mu,f,mu,r分别为前、后两车非簧载质量;Ur为前车后悬架作动器产生的作用力;Uf为后车前悬架作动器产生的作用力;m1,m2分别为前、后车的质量.
由此可得力学方程式为
(11)
上文已优化得到两辆货车的最优车距,进而可得Sa,Sb.
汽车主动悬架系统数学模型动力学方程为
(12)
系统动力学微分方程可写成状态空间方程的形式,即

(13)

系统矩阵A为
(14)
控制矩阵B,输入矩阵F分别为
(15)
(16)
采用超轴距预瞄系统,通过车与车之间的信息交互,悬架控制器能提前得出经过前方路面时的最佳控制力,及时传达给后车,使其提前做出应对,通过车身加速度、悬架动挠度、轮胎动载荷3个性能指标评价乘坐的舒适性[15],将各项指标加权系数写成矩阵J的形式,可得
.
(17)
在矩阵J形式中,N,R,Q的计算式分别为
(18)
(19)
(20)
由黎卡提方程求出最优控制反馈增益矩阵K,K由车辆参数及加权系数决定,有
PA+ATP-(PB+N)R-1(BTP+NT)+Q=0,
(21)
K=R-1·(BT·P+NT).
(22)
式(21),(22)中:P为黎卡提方程中的解.
由X(t)可得t时刻前、后作动器的最优控制矩阵为
U(t)=-KX(t)
.
(23)
采用二阶帕德(Pade)近似法将最优控制矩阵转换为状态空间的形式,有
(24)
式(24)中:a0=12/τ2,τ为前、后轮激励之间的时间延迟;a1=6/τ;a2=1.

系统的输入方程为
w2(t)=w1(t-τ)=Cηη(t)+w1(t)=η1(t)+w1(t)
.
(25)
式(25)中:Cη=[1 0].得到具有轴距预瞄信息并带有附加状态矢量η的系统状态方程为
(26)

2.3 仿真分析
采用滤波白噪声的时域表达式作为路面输入模型,前车后轮处路面输入方程为
(27)
式(27)中:G0为路面不平度系数;uc为后车前进速度;f0为下截止频率.
由于时间的滞后,后车前轮处路面输入方程可写为
(28)
式(28)中:τ=(Sa+Sb)/uc.
以解放J6型载重货车为研究对象,设车辆行驶的速度(即后车前进速度)uc=20 km·h-1,系统采样时间段Ts=0.002 5 s,在Matlab/Simulink平台建立半车模型,仿真参数,如表1所示.

表1 仿真参数的取值Tab.1 Value of simulation parameters
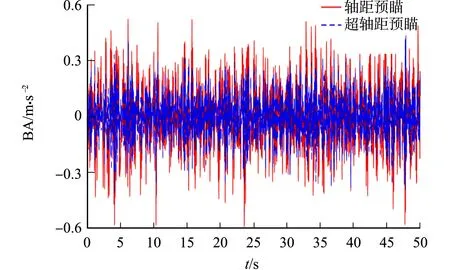
图7 车身加速度仿真图 Fig.7 Simulation diagram of car body acceleration

图8 轮胎动位移仿真图 图9 悬架动行程仿真图 Fig.8 Simulation diagram of Fig.9 Simulation diagram of tire dynamic displacement suspension dynamic travel
在B级路面上,采用超轴距预瞄控制方法对悬架性能参数(车身加速度、轮胎动位移和悬架动行程)进行仿真分析,结果如图7~9所示.图7~9中:BA为车身加速度;DTD为轮胎动位移;SWS为悬架动行程(下同略).由图7~9可知:超轴距预瞄与轴距预瞄具有相近的响应特性;车身加速度的轴距预瞄为0.381 m·s-2,超轴距预瞄为0.288 m·s-2,下降幅度为24.5%;轮胎动位移的轴距预瞄为5.853 mm,超轴距预瞄为4.186 mm,下降幅度为28.5%;而悬架动行程的轴距预瞄为16.836 mm,超轴距预瞄为15.769 mm,其下降幅度为6.9%.
3 车身加速度的单目标寻优算法
在超轴距预瞄的主动悬架模型中,套用了轴距预瞄计算方法,由于簧载总质量等参数采用当量参数进行替代,车速稳定性条件难以达成,可能会造成计算及控制中的偏差.此外,始发车的控制效果对车队整体的影响较大,而遗传算法是一种以群体和遗传操作为基础进行监测和评价的迭代优化算法,新生代比前代更加适应环境[16],可获得更好的个体和最优解.因此,进一步采用悬架参数单目标优化的遗传算法对车身加速度进行仿真分析,以实现货车悬架控制效果的优化.
遗传算法的求解问题机制描述为

(29)
式(29)中:x为车队中某一辆货车;f(x)为目标函数;gh(x)为约束条件;z为约束条件的个数;Umin为算法中变量的下限;Umax为算法中变量的上限.
3.1 设计变量
设计变量Y=[Ks,f,Ks,r,Cf,Cr],Ks,f取126.47~319.20 Mg·m-1;Ks,r取893.62~993.50 Mg·m-1;Cf为后车前悬架的阻尼,取0~20 kN·s·m-1;Cr为前车后悬架的阻尼,取0~30 kN·s·m-1.
3.2 约束条件与目标函数
由于受碰撞器的限制,悬架动挠度必须限制在一个安全的范围内,以保证货车行驶的安全性,有
D1(Y)=Z1-Z3≤Dmax,D2(Y)=Z2-Z4≤Dmax.
(30)
式(30)中:D1(Y)为前车后轴的动挠度;D2(Y)为后车前轴的动挠度;Dmax为允许最大动挠度,取80 mm.
车队货车作业任务主要是以运输玻璃为主,为了提高汽车平顺性和货物的完好性,以车身加速度均方根值a(Y)为优化指标.
车身加速度的均方根值为
.
(31)
式(31)中:d为货车结对对数;te为第e组车经过此路段的某一时刻.
为了对车队货车不同车速行驶时的车身加速度进行优化,选择3种车速(uc=20,40,60 km·h-1)进行分析,以货车经常行驶的B级路面为路面输入.
3.3 仿真与分析结果
采用标准遗传算法(SGA)处理单目标优化问题,对车队运输重复性特征、相同车型及固定线路而言,该方法简单实用,可以高效地完成迭代寻优.
在Matlab环境下进行仿真,B级路面上车队货车车速分别为20,40,60 km·h-1,优化前、后车身加速度仿真图,如图10~12所示.

(a) 优化前 (b) 优化后图10 优化前、后车身加速度仿真图(uc=20 km·h-1) Fig.10 Simulation diagram of car body acceleration before and after optimization (uc=20 km·h-1)

(a) 优化前 (b) 优化后图11 优化前、后车身加速度仿真图(uc=40 km·h-1) Fig.11 Simulation diagram of car body acceleration before and after optimization (uc=40 km·h-1)
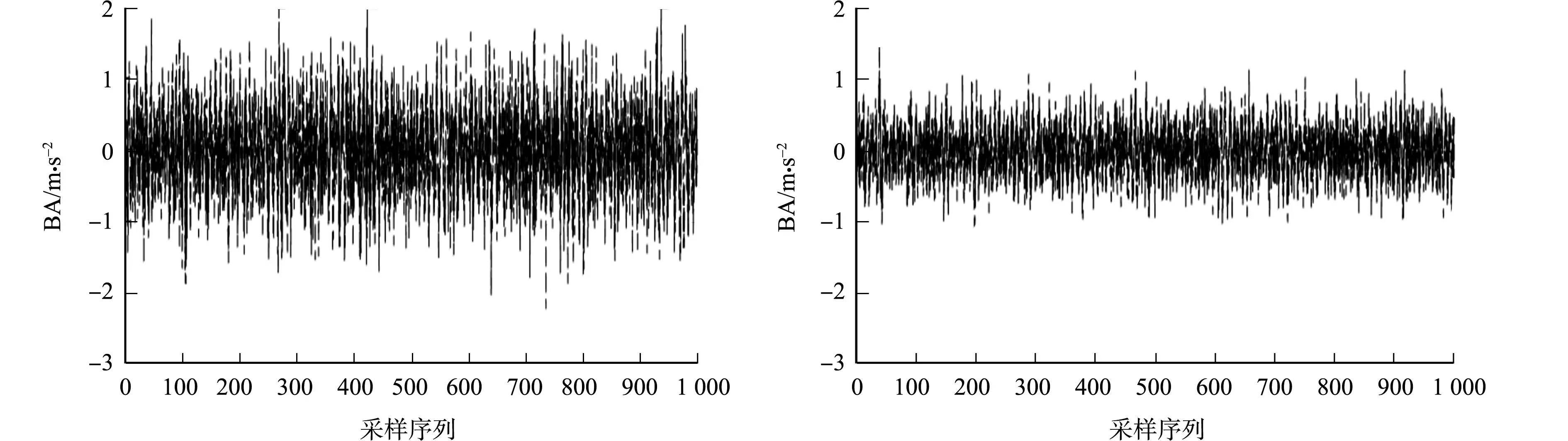
(a) 优化前 (b) 优化后图12 优化前、后车身加速度仿真图(uc=60 km·h-1) Fig.12 Simulation diagram of car body acceleration before and after optimization (uc=60 km·h-1)
经过相关的计算可知:当uc=20 km·h-1时,优化前、后车身加速度均方根值从0.381 m·s-2下降至0.288 m·s-2,下降幅度约为24%;当uc=40 km·h-1时,优化前、后车身加速度均方根值从0.721 m·s-2下降至0.387 m·s-2,下降幅度约为46%;当uc=60 km·h-1时,优化前、后车身加速度均方根值从0.942 m·s-2下降至0.422 m·s-2,下降幅度约为56%.
需要指出的是,超轴距预瞄的寻优是整个车队的车辆按照发车顺序进行寻优迭代,不需要每辆车都进行相同的寻优过程,或等待某车辆完成寻优后复制到其他车辆.因此,该优化方法的迭代整体效率更高,更适合工程实际应用.
4 结论
1) 提出结对交互辅以地理信息监测的网络构架,降低了数据交互量,确保了短车距和长车距两种模式下通讯的稳定性.
2) 通过对车身加速度、轮胎动位移和悬架动行程3个悬架性能指标的分析可知,在轴距预瞄基础上发展而来的超轴距预瞄具备相似的控制响应特性.
3) 基于车身加速度,采用标准遗传算法处理单目标优化问题,可实现货车的迭代优化、超轴距预瞄的寻优,具有更高效率的迭代过程.
