北斗GBAS机载接收机最后进近航段偏差研究
2021-09-26刘瑞华
刘瑞华,高 祎
(中国民航大学电子信息与自动化学院,天津 300300)
近年来,随着北斗卫星导航系统(BDS,Beidounavigation satellite system)建设和服务能力的快速发展,围绕北斗的各项研究正在不断展开。作为下一代精密进近着陆系统的重要选择——陆基增强系统(GBAS,ground-based augmentation system)能够弥补仪表着陆系统(ILS,instrument landing system)的固有缺陷,为机载用户提供更高标准的所需性能导航(RNP,required navigation performance)。
目前,美国Honeywell 公司研发生产的局域增强系统(LAAS,local area augmentation system)地面站已获得美国联邦航空管理局的系统设计认证,成为全球唯一一个获得认证的GBAS。随后该公司完成了基于III 类精密进近的LAAS 地面站和机载系统原型设计,并完成了演示验证工作。中国也是GBAS 应用的积极倡导者和实践者,先后于上海浦东国际机场和天津滨海国际机场完成了基于Honeywell 公司的SLS-4000型GBAS 设备和国产GBAS 系统的演示验证工作[1],但迄今为止,中国有关GBAS 机载设备的适航标准仍在研究制定之中。
在GBAS 系统中,系统精度主要受以下因素影响:①位置估计误差;②确定最终进近路径时出现的误差;③计算偏离预期路径时出现的误差[2]。“偏差”作为精密进近引导输出的重要参数,刻画了飞机相对于预期参考路径的偏离程度,同时也是衡量GBAS 机载接收机的重要性能指标。美国航空无线电委员会(RTCA,Radio Technical Commission for Aeronautics)于2017年颁布的《GPS 局域增强系统机载设备最低运行性能标准》(DO-253D)[3]中明确规定,GBAS 机载接收机应在收到支持所选进近方式的必要有效信息后,计算并输出精密进近引导信息,其中包括横向和垂直偏差数据。
目前,国内有关GBAS 机载接收机最后进近航段(FAS,final approach segment)偏差的研究还相对较少。文献[4]分析推导了偏差的计算公式,给出了偏差的主要影响因素,但缺少严格的仿真测试。针对以上研究现状,参照国际民航组织(ICAO,International Civil Aviation Organization)附件10 和RTCA 的相关标准,结合中国北斗卫星导航系统现状,给出了GBAS 机载接收机最后进近航段偏差的定义和解算过程,并进行仿真校验。研究结果可为中国北斗GBAS 机载接收机适航标准的制定提供理论支持。
1 GBAS 机载设备的组成
RTCA DO-253D 中将机载设备按功能分为甚高频数据广播(VDB,VHF data broadcast)子系统及位置与导航(PAN,position and navigation)子系统。前者通过飞机机载甚高频天线接收GBAS 地面站播发的差分修正信息和下滑道信息。后者通过接收VDB 报文和卫星信号进行差分修正、完好性计算等过程,并输出位置、速度、时间和相对于最后进近航段的偏差等信息,完成精密进近引导[4]。
根据RTCA 对GBAS 机载设备功能和工作流程的描述,给出了GBAS 机载设备的组成和工作流程,如图1 所示。

图1 GBAS 机载设备的组成和工作流程Fig.1 Composition and working process of GBAS airborne equipment
图1 中:消息类型1(MT1)提供差分伪距修正值等信息;消息类型2(MT2)提供完好性参数等信息;消息类型4(MT4)提供1 组或多组FAS 数据,且每个FAS 数据都定义了1 条独立的精密进近参考路径;涉及偏差解算的部分用阴影表示。
2 最后进近航段偏差解算
在飞机的最后进近航段,机载PAN 设备通过接收北斗卫星信号和GBAS 地面站播发的报文数据(MT1)确定飞机的位置后,根据地面站播发的最后进近航段数据(MT4)确定1 条下滑道,并计算飞机相对于该下滑道的横向偏差和垂直偏差,给出横向和垂直引导信息,从而引导飞机成功着陆。偏差的解算主要包括GBAS 定位解算和基于最后进近航段的单位矢量计算两个过程。
2.1 GBAS 定位算法
机载PAN 设备利用载波相位对伪距进行平滑,并通过伪距差分消除基准站和机载用户之间的大部分公共误差,最后利用加权最小二乘法来实现用户的定位解算[5]。定位算法原理流程图如图2 所示。
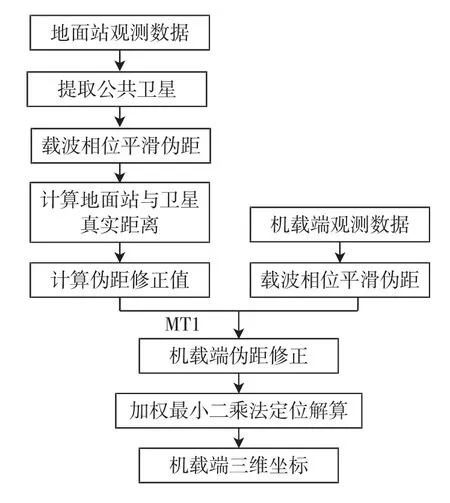
图2 GBAS 定位算法原理流程图Fig.2 Principle flow chart of GBAS positioning algorithm
2.1.1 载波相位平滑伪距
载波相位平滑伪距技术是GBAS 定位算法的重要组成部分。利用高精度的载波相位观测值对测码伪距进行平滑,能够有效抑制伪距测量中的噪声和多径效应的影响,大大提高伪距的测量精度。
设历元k 时刻的伪距和相位观测方程为

式中:ρik和φik为历元k 时刻接收机测量的第i 颗卫星的伪距值和载波相位值;Rik为历元k 时刻第i 颗卫星
到接收机的几何距离;δu和δi分别为接收机钟差和卫星钟差;λ 为载波波长;N 为整周模糊度;ερ和εφ为接收机噪声。
对相邻两历元的伪距和相位观测方程作差得
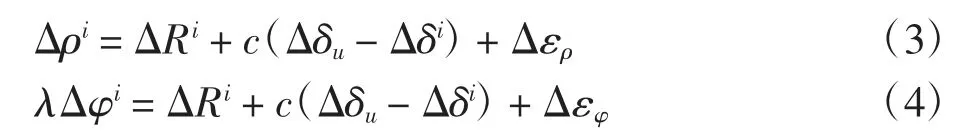
将式(3)和式(4)整合,即可得到一种既无整周模糊度又相对平滑的伪距测量值[6],即
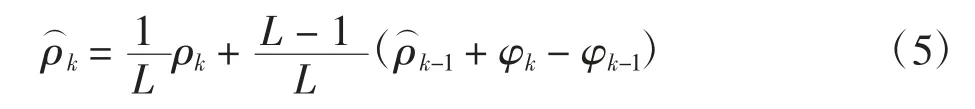
2.1.2 伪距差分
在坐标精确已知的地面基准站上安装接收机连续测量可见卫星i 的第n 个接收机测量的伪距ρin,利用两点间坐标公式解算出卫星与地面基准站的几何距离Rin,则地面基准站M 个参考接收机与第i 颗卫星的伪距修正值可表示为

利用前后历元的伪距修正值之差即可求出其变化率
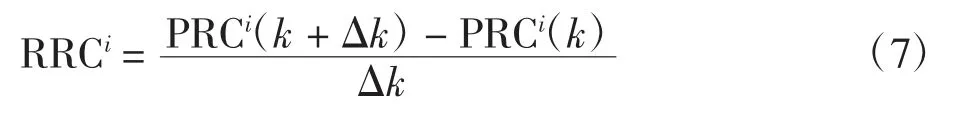
基准站将PRC 和RRC 等伪距修正信息通过VDB 以MT1 的形式发送给机载用户,机载接收机根据接收到的修正信息对已测伪距进行修正。机载接收机在t 时刻第i 颗卫星经过修正后的伪距测量值为
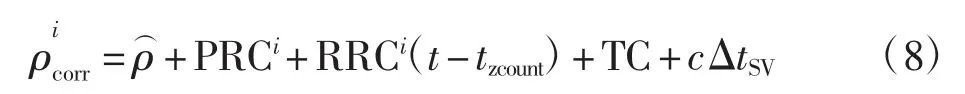
式中:tzcount为PRC 的适用时间;TC 为对流层修正值;c为光速;ΔtSV为卫星时钟修正值。
2.1.3 加权最小二乘法定位解算
当机载接收机获得了多于4 个经过修正的伪距测量值时,基于加权最小二乘法的线性测量模型解算飞机位置。解算方程为

式中:Δy 为差分修正前后伪距值之差形成的矢量;Δx为用户坐标和卫星钟差构成的四维矩阵;G 为观测矩阵;ε 为测量误差矢量,设其中每项误差均服从均值为0 的高斯分布。
由加权最小二乘法可得Δx 的估计值为

式中:S 为投影矩阵;W 为加权最小二乘矩阵;观测矩阵G 的第i 行可表示为
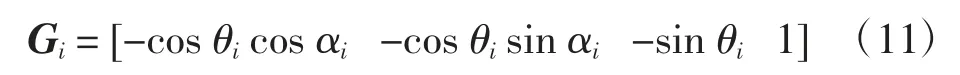
式中θi和αi分别为第i 颗卫星的高度角和方位角。
2.2 GBAS 最后进近航段
偏差定义基于RTCA DO-246E 中定义的最后进近航段数据,如图3 所示,其中:LTP/FTP 为着陆入口点/虚拟入口点,是跑道入口的中心点,且在FAS 数据中包含了该点基于标准WGS-84 椭球参考系的经纬高坐标;FPAP 为飞行航道校正点,用于校正飞机航道(在FAS 数据中,FPAP 坐标并不直接提供,而是提供了相对于LTP/FTP 的经度和纬度);“长度补偿”表示跑道末端与FPAP 沿跑道中心线方向的偏移;TCH 为入口点跨越高度,表示LTP/FTP 上方FAS 的所需高度,同时,下滑道角度(GPA)和LTP/FTP 处的跑道宽度(CW)也会在FAS 数据中提供[7];GRP 为飞机引导参考点,表示机载接收机输出的飞机位置;TCP 为入口交叉点,表示垂直于跑道的平面在LTP/FTP 上方与FAS相交的点;GPIP 为下滑道拦截点,是FAS 和跑道中心线的交叉点,表示飞机触地着陆点;GERP 为高度角参考点,该点与GPIP 沿跑道方向的水平距离一般设为0、150 m;GARP 为方位角参考点。
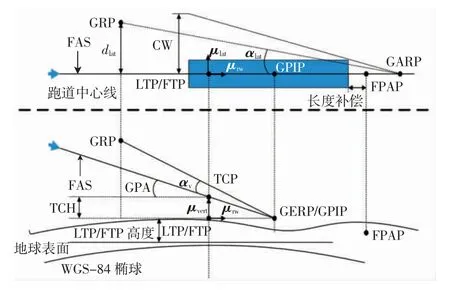
图3 最后进近航段俯视图与剖面图Fig.3 Top view and cross-sectional view of final approach segment
为便于计算,在地心地固坐标系(ECEF,earthcentered,earth-fixed)下定义3 个方向的单位矢量,分别为垂直方向单位矢量μvert,横向单位矢量μlat和沿跑道中心线方向单位矢量μrw。
垂直方向单位矢量可表示为

为了定义μlat和μrw,计算从LTP/FTP 指向FPAP的飞行航道校正单位矢量,即


沿跑道中心线方向的单位矢量可表示为

基于3 个单位矢量和上述对FAS 的定义,确定了3 个参考平面:包含LTP/FTP、TCP、FPAP 的垂直参考平面(横向偏差参考平面);包含μvert和FPAP 的横向参考平面;包含μlat和μrw的本地水平面。
2.3 偏差解算
2.3.1 横向偏差
横向偏差包括直线横向偏差和角度横向偏差,其中,直线横向偏差为GRP 与横向偏差参考平面之间的距离,角度横向偏差为GRP 与GARP 的连线相对的跑道中心线的角位移,如图4 所示。
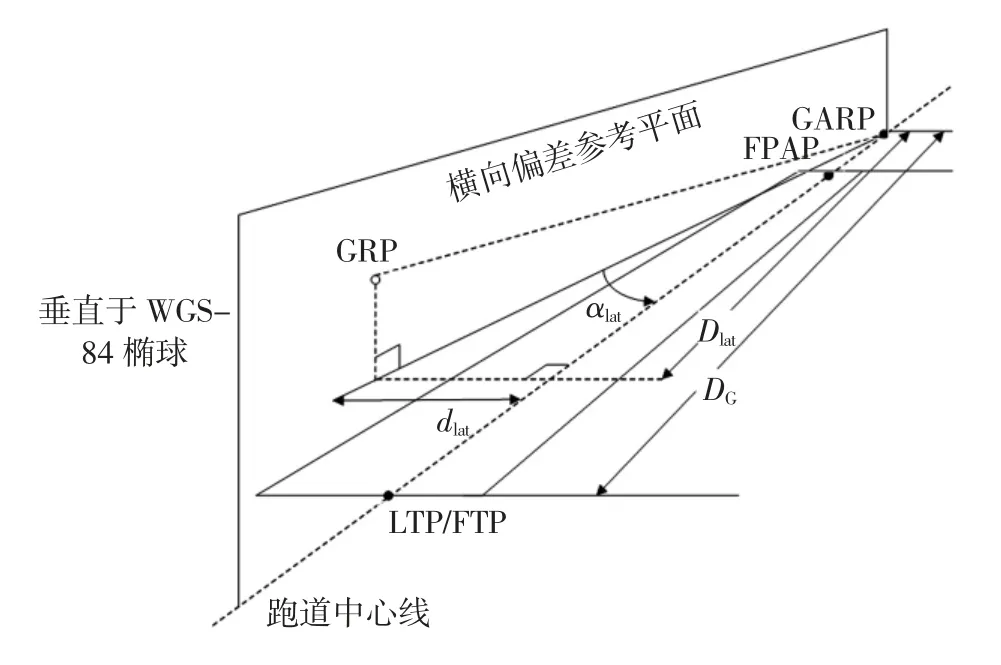
图4 横向偏差示意图Fig.4 Schematic diagram of horizontal deviation
横向偏差可分为以下3 步进行解算。
(1)计算从地球中心到GARP 的方向向量

式中DGARP为FPAP 与GARP 间的距离,通常设为305m。
(2)计算直线横向偏差

(3)将直线横向偏差转换为角度横向偏差,即

机载PAN 设备输出的角度横向偏差一般以横向调制深度差表示,即
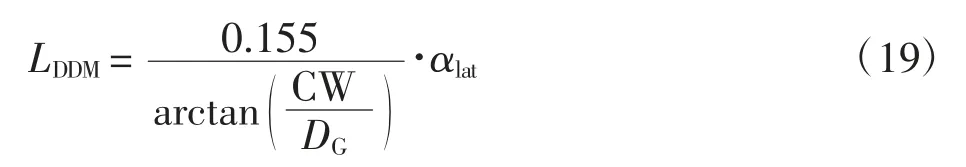
式中DG为从GARP 到LTP/FTP 的距离。横向偏差参考平面即为所有LDDM=0 的点确定的平面。
为实现GBAS 系统与仪表着陆系统的兼容性,ICAO 附件10[8]中将LDDM=±0.155 所限定的区域称为航道扇区,如图5 所示,此时的角度横向偏差为满刻度偏转αlat,FS。通常CW=105 m 时,LDDM=0.155 且最大航道扇区不超过6°,即机载PAN 设备输出的最大角度横向偏差[9-10]不超过±3°。
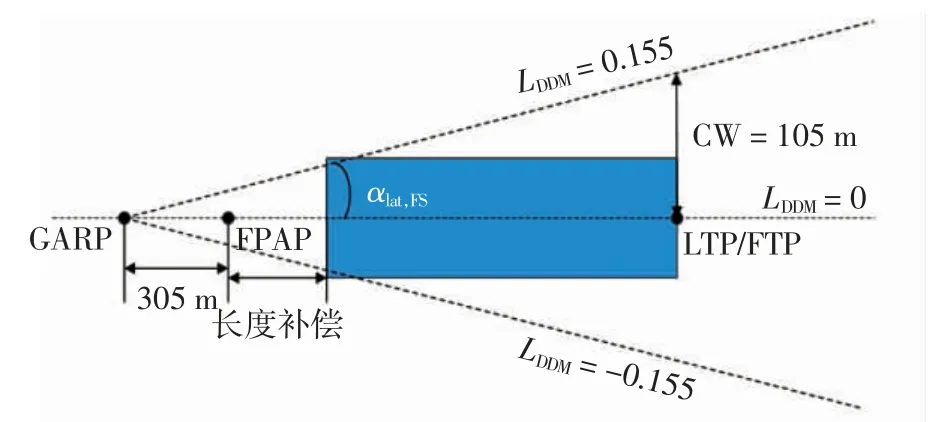
图5 航道扇区Fig.5 Channel sector
2.3.2 垂直偏差
为更准确地定义垂直偏差,首先,定义了垂直偏差参考平面:包含FAS 的圆锥体表面,其顶点位于GERP(该点可位于GPIP 处,也可位于从GPIP 横向偏移150 m 的固定GERP 偏移量处)且对称轴平行于过LTP/FTP 的垂直方向向量,如图6 所示。和横向偏差类似,垂直偏差包括直线垂直偏差和角度垂直偏差。其中直线垂直偏差为GRP 与圆锥体表面的垂直距离,角度垂直偏差是其正弦值为直线垂直偏差与GRP 到GERP 的距离之比的角。
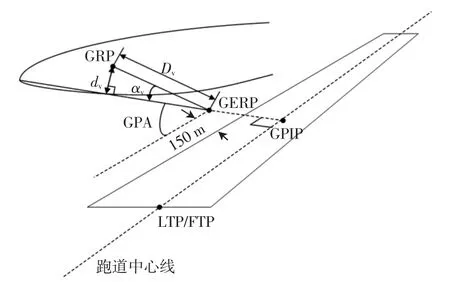
图6 垂直偏差示意图Fig.6 Schematic diagram of vertical deviation
垂直偏差可分为以下两步进行解算。
(1)计算从地球中心到GERP 的方向向量

式中DGERP为150 m 的GERP 固定偏移量。
(2)计算GRP 相对于理想下滑道的角度垂直偏差
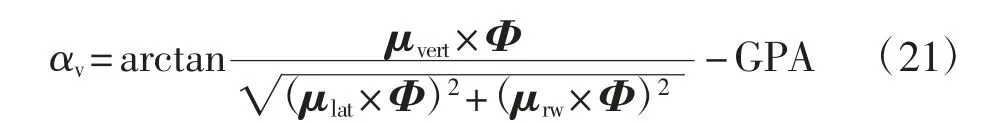
此外,直线垂直偏差可由下式求得,即

机载PAN 设备输出的角度垂直偏差一般以垂直调制深度差表示,即

为实现GBAS 系统与仪表着陆系统的兼容性,ICAO 附件10 中将VDDM=±0.175 所限定的区域称为下滑扇区,此时的角度垂直偏差为满刻度偏转,可表示为

式中GPA 为下滑道角度,通常取3°。根据式(24)可得机载PAN 设备输出的最大角度垂直偏差不超过±0.75°。
3 仿真校验
基于以上FAS 的分析,参考天津滨海国际机场34L跑道坐标仿真生成一条直线型精密进近着陆航径,如图7 所示。该航径作为理想进近与着陆路线,是下文偏差仿真的参照对象。

图7 GBAS 最后进近航段三维仿真图Fig.7 3D simulation diagram of final approach segment of GBAS
该航径采用由最后进近点(FAP)(39.205,117.297,600)、LTP/FTP(39.111,117.354,3.7)及FPAP(39.137,117.338,3.7)所确定的3°理想下滑道。进近着陆过程总用时120 s,其中,进近过程耗时100 s,触地之后沿跑道滑行耗时20 s。选用本地参考坐标系,其参考原点为LTP/FTP。根据DO-253D 中对GBAS 机载设备输出参数频率的要求,仿真以5 次/s 的频率模拟航径,共计600 个定位点。选取其中A、B、C 3 点作为静态观测点。
基于上述理想精密进近着陆航径,分别在静态和动态两种场景下对机载接收机偏差输出进行仿真分析。
3.1 静态仿真
1)仿真条件设置
采用中国卫星导航系统管理办公室提供的第755周BDS 历书数据(2020年7月)。卫星遮蔽角为5°,4 个基准站坐标分别为(39.135,117.344,3.79)、(39.136,117.344,3.79)、(39.135,117.346,3.79)、(39.134,117.346,3.79)。GBAS 基准站接收机和机载接收机分别选用RTCA DO-245A 中定义的A 类和B 类接收机。残余对流层不确定数为33,对流层大气高度为7 600 m,电离层平均厚度为350 km。观测时长为24 h,观测步长为100 s,总计样本数为864 个。仿真软件为Matlab R2018b。
2)仿真结果与分析
如图8 所示,1 天内天津滨海国际机场可见卫星最多为18 颗,最少为11 颗,能够满足GBAS 定位需求。
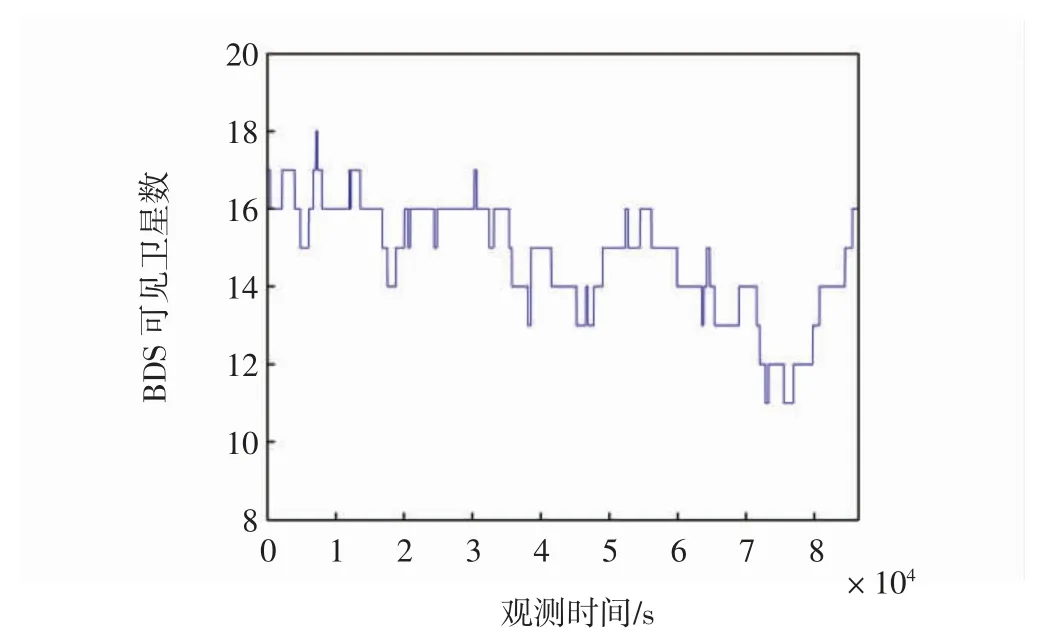
图8 天津滨海国际机场北斗可见卫星Fig.8 Beidou visible satellite in Tianjin Binhai International Airport
图9 为GBAS 基准站无故障情况下A 点一天内机载接收机计算的横向偏差和垂直偏差变化曲线。从图9 中可以看出:当基准站无故障时,横向偏差在-0.34°~-0.25°范围内变化,波动范围不超过±0.05°,均未超过上述推导的横向偏差阈值(±3°);垂直偏差在-0.08°~0.04°范围内变化,波动范围不超过±0.06°,均未超过上述推导的垂直偏差阈值(±0.75°)。
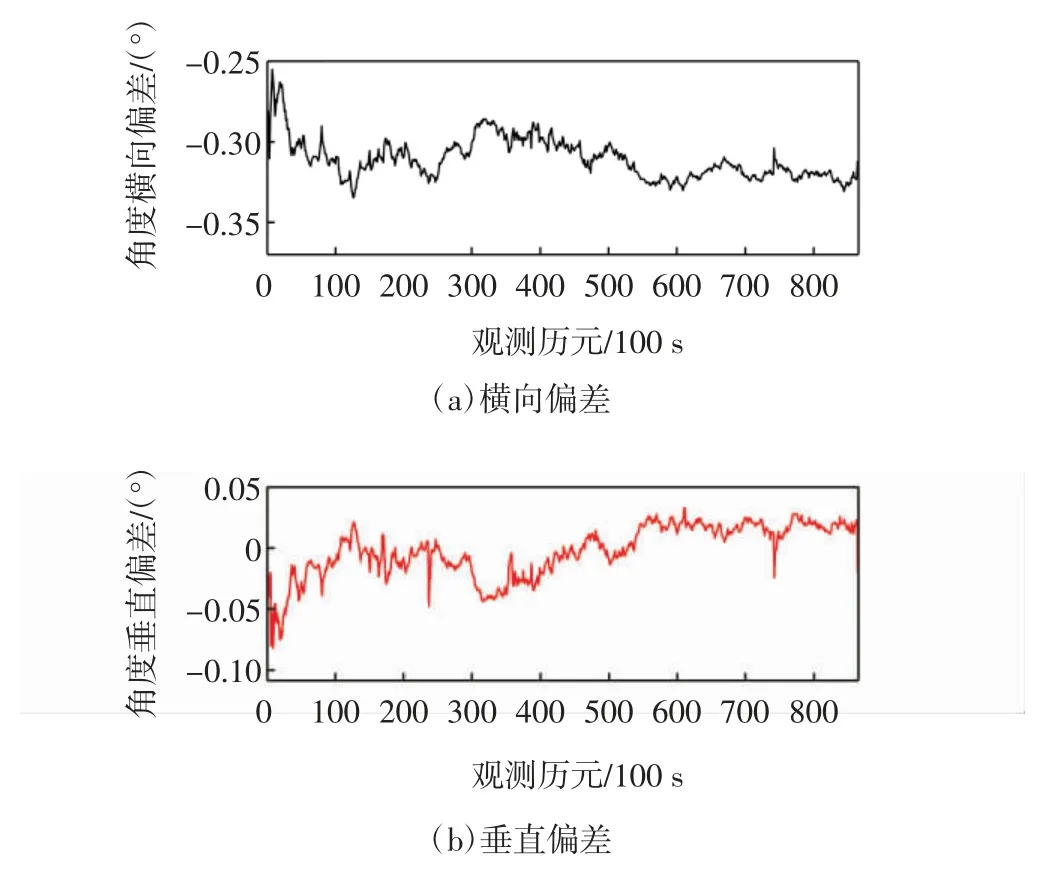
图9 A 点静态测试偏差仿真Fig.9 Deviation simulation of static test at point A
为研究GBAS 基准站故障对机载接收机偏差计算的影响,实验人为地在第600~800 观测历元之间对其中1 个基准站接收机加入误差。由于任何GBAS 基准站故障均可建模成一个斜坡和一个阶跃模型,故对两种故障模型分别进行仿真分析[11]。
当在基准站接收机的伪距修正值上分别添加大小为10 m 的阶跃故障(以B 点为例)和斜率为1/500的斜坡故障(以C 点为例)时,仿真结果分别如图10和图11 所示,可以看出,当引入阶跃故障和斜坡故障后,机载端输出偏差值的变化相应的也呈阶跃型和斜坡型变化,但始终未超过其阈值,说明此时机载接收机计算的偏差值能够满足精密进近引导输出的要求。
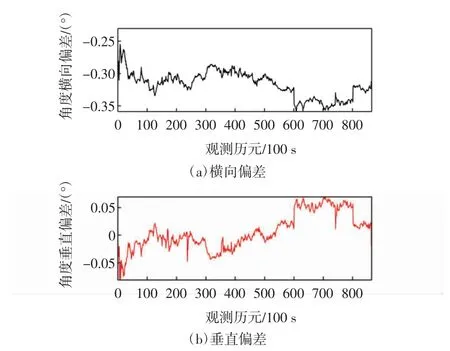
图10 B 点阶跃故障下的偏差仿真Fig.10 Deviation simulation under step fault at point B
3.2 动态仿真
1)仿真条件设置
机载接收机航径采用上述仿真生成的直线型精密进近着陆航径,观测时长为600 s,观测步长为1 s,总计样本数为600 个。为保证实验结果的准确可靠性,对上述过程进行10 次蒙特卡洛重复实验,其他仿真条件与静态仿真时保持一致。
2)仿真结果与分析
图12 为飞机最后进近航段机载接收机计算的横向偏差和垂直偏差变化曲线。
从图12 中可看出,10 次蒙特卡洛重复实验结果的变化趋势大体相同,且横向偏差在-0.36°~-0.14°之间变化,垂直偏差在-0.06°~0.11°之间变化,两者均未超过相应阈值。由于飞机距LTP/FTP 距离逐渐减小,在此过程中飞机逐渐对准下滑道,故横向偏差总体呈减小趋势。
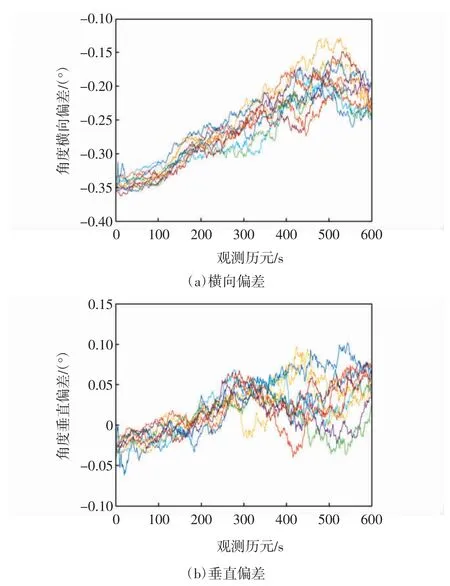
图12 动态测试偏差仿真Fig.12 Deviation simulation of dynamic test
4 结语
从GBAS 实际应用出发,根据RTCA DO-253D 中对机载PAN 设备偏差输出的要求,详细介绍了偏差的定义和解算过程,并结合相关标准文献给出机载PAN设备偏差输出的阈值。从仿真结果可以看出,静态和动态场景下机载PAN 设备计算的横向偏差和垂直偏差均能够较好地满足阈值要求,即在当前北斗星座条件下,GBAS 机载PAN 设备能够在实现GBAS 系统与仪表着陆系统兼容的前提下,为飞机提供满足RTCA DO-253D 中要求的垂直和水平引导信息。研究成果可为北斗GBAS 机载PAN 设备的研制和适航标准的制定提供理论支持。
