基于飞行程序交叉点的机场群航班时刻优化

翟文鹏，王玮卿，杨群亭

（中国民航大学空中交通管理学院，天津300300）

一个机场所有航班时刻组合成航班时刻表，科学合理的航班时刻表将会提升机场的整体运行效率，因此，航班时刻优化是减少延误的有效手段之一。国内外关于航班时刻优化的研究较多。Takeichi[1]提出通过延迟累积的解析来优化飞行时间，解决了延误累积问题。Zografos 等[2]以航班时刻总调整量最小化和不可接受调整量最小化为基础建立双目标规划模型，使配置结果更易被航空公司所接受。陈亚青等[3]基于航班延误成本和航路耦合容量建立模型并将航班时刻总调整量最小作为目标函数。胡明华等[4]建立了航班时刻优化模型并采用改进的匈牙利算法进行求解，以达到航空器地面等待时间和航班时刻调整量整体最小的目标。左杰俊等[5]从流量管理者角度出发，以航班最大调整量最小和总延误时间最少为目标函数建立航班时刻优化模型，并运用Lingo 软件进行快速求解。杨新湦等[6]针对中国大型机场国内航线高峰时刻运力不足等情况提出了航线机型优化模型及航班时刻优化方法，并利用Simmod 软件进行仿真验证。汪梦蝶等[7]提出可接受调整量水平的概念对航班时刻进行优化，均衡了航空公司效益和机场运行效率，并采用AirTOP软件进行模拟验证。康瑞等[8]提出一种基于航空器交叉滑行冲突概率的模型并进行仿真验证。王倩等[9]建立基于航空公司公平性的航班时刻优化模型。陈华群[10]采用全局动态规划策略实现了所有航站、航班和机队的全局运行控制优化。李昂等[11]构建以提升航班正点率为目标的机场群现有航班时刻优化模型。

以上研究模型主要以航班时刻总调整量最小为目标函数，却忽视了将航班时刻调整量合理分配到各航空公司；约束条件主要集中在机场容量，进、离港港口容量及最小过站时间等方面，虽可解决一部分航班延误，但却忽略了具体的飞行程序，尤其是飞行程序交叉点附近航班的聚集情况，这是限制航班延误进一步减少的原因之一。因此，基于传统航班时刻优化模型，将航班时刻调整量合理分配到各航空公司，然后增加程序交叉点容量的限制条件对航班时刻进行优化调整。将航班计划导入仿真模型进行模拟验证，在减少航班延误的同时，可降低管制员调配航空器冲突的次数。

1 航班时刻优化原则

1.1 安全间隔

程序交叉点是指不同进场程序之间的交点，不同进场程序的航空器到达同一程序交叉点时的间距需满足安全间隔。

在进场的非进近阶段，不足300 m 以上的垂直安全间隔的航空器之间须满足水平安全间隔，此时的水平安全间隔必须同时满足最小尾流间隔（取决于前机与后机的机型）和区域管制的最小雷达间隔（10 km），两者结合后不同机型的水平安全间隔如表1 所示。

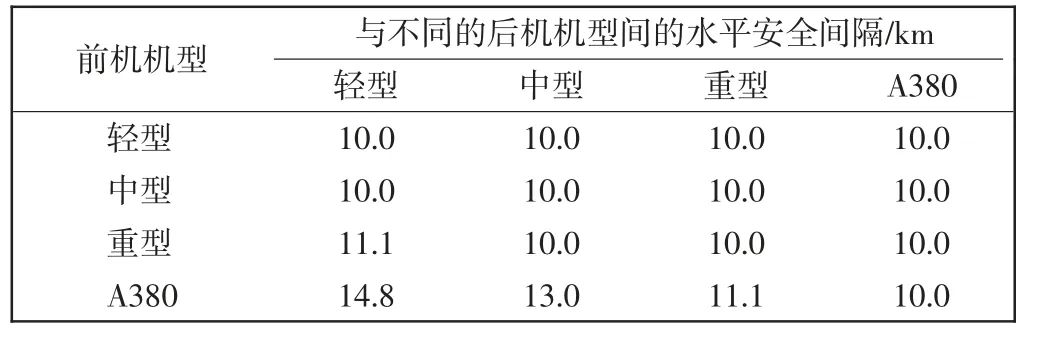
表1 不同机型间的水平安全间隔Tab.1 Horizontal safety interval between different aircraft models

针对非雷达引导区的航空器，管制员调配航空器安全间隔的方式首先是调配高度，使航空器之间的高度差满足垂直安全间隔，其次是调节航空器的飞行速度，使其水平间隔满足安全要求。

1.2 程序交叉点容量

图1 为上海虹桥国际机场（简称虹桥机场）标准仪表进场程序的局部截图，为使航班时刻优化模型更具现实可行性，不使用SUP-61A（by ATC）和AND-62A（by ATC）的进场程序。

以程序交叉点JTN 为例，JTN 最低允许高度为1 800 m，JTN 前序程序定位点SS206 的最高允许高度为2 400 m，由此可知，如果航空器的运行严格按照程序规定，则JTN 的航空器允许飞行高度为1800～2400m。当航空器的水平间距不满足水平安全间隔时，管制员优先考虑调配垂直间隔，使其高度差大于300 m，因此，在一个水平安全间隔的范围内，JTN 的容量为3 架次。

图1 中，通过AND 和PUD 两个进港方向的航班，当第1 个航班经过JTN 时，在这个航空器之后的一个安全间隔范围内，最多允许存在其他2 架满足300 m垂直间隔的航空器。如果航空器数量超过程序交叉点容量，则需要调配航空器速度以满足水平安全间隔的要求，这会影响后续航班的正常运行，增加航班的延误时间。

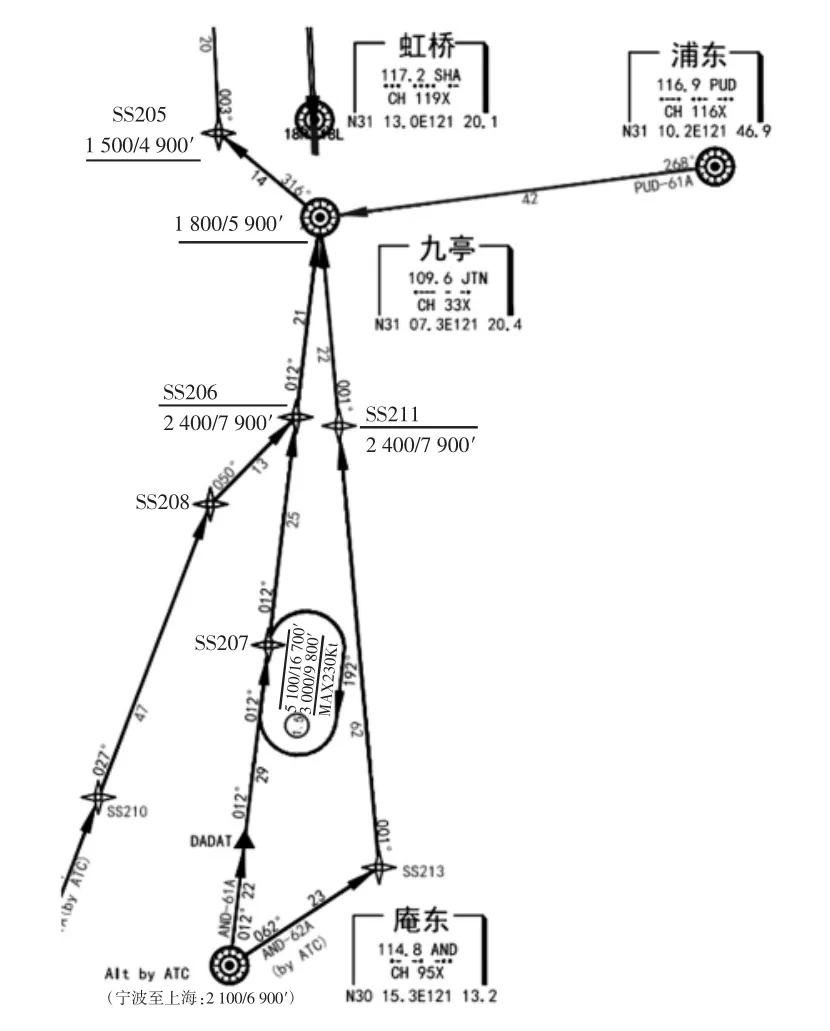
图1 上海虹桥国际机场标准仪表部分进场程序Fig.1 Partial approach procedure of the standard instrument in Shanghai Hongqiao International Airport

将程序交叉点容量约束加入航班时刻优化模型，能一定程度上缓解程序交叉点附近的航班聚集情况，降低管制员调配冲突航班的压力。

1.3 时刻调整量分配合理性指标

航班时刻优化会产生时刻调整量，即航空公司申请时刻与优化后分配时刻的差值。对机场群航班时刻进行优化时，合理分配由于时刻优化而产生的时刻调整量可提高机场群运行效率，同时可避免航班时刻调整量过多分配到某航空公司的情况。以航空公司时刻调整量的方差作为机场群航班时刻调整量分配合理性指标（数值越小表示时刻调整量分配越合理），其计算方法为每个航空公司与机场群的航班时刻平均调整量之差的平方和，再除以机场群内航空公司的总数。

为了使时刻调整量分配合理性指标设置更加科学，计算航空公司航班时刻平均调整量时使用该航空公司内所有航班时刻平均调整量，而不使用存在时刻调整量的航班时刻平均调整量。举例说明采用后者进行计算的缺点，假设航空公司A 和B 各有10 个航班，航空公司A 的1 个航班调整了10 min，而航空公司B的9 个航班都调整了10 min，则这两个航空公司的时刻调整量合理性指标是一样的，但可明显看出，该分配时刻调整量的方式是完全不合理的。

假设1 个时间片为5 min，有6 个航班m1，m2，…，m6且单个航班时刻调整量不超过30 min，即6 个时间片，其中，m1，m2，m3是航空公司A 的航班，m4，m5，m6是航空公司B 的航班，容量约束为每3 个时间片2 个航班。

表2 和表3 为不同优化方式优化后的航班调整表，其中：灰色格子表示航班m1，m2，…，m6申请的时刻；航空公司A 的航班优化后分配的时间片用“#”表示；航空公司B 的航班优化后分配的时间片用“*”表示。

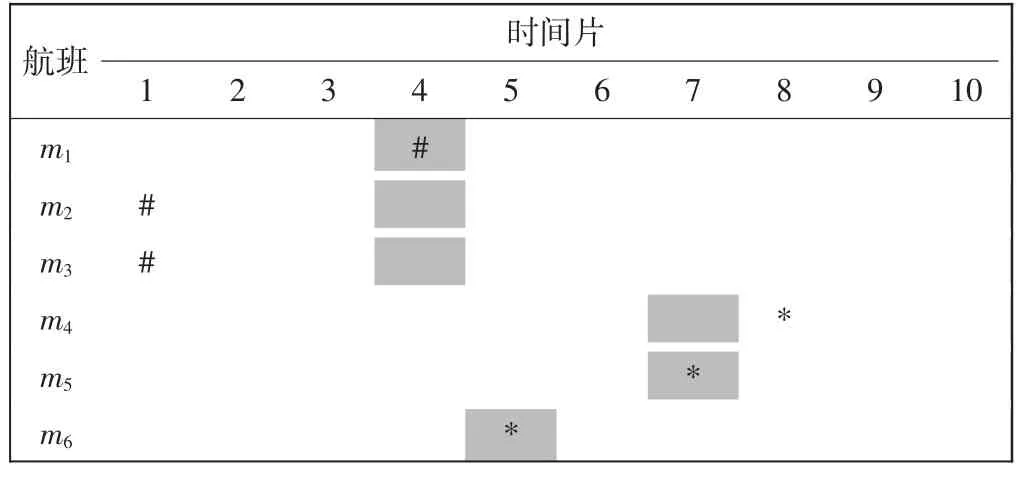
表2 单目标优化后航班调整表Tab.2 Flight adjustment table after single objective optimization

表2 为仅考虑航班时刻总调整量最小的情况，即单目标优化。以表2 为例计算合理性指标，m2和m3的时刻调整量为15 min，m4为5 min，航空公司A 的航班时刻平均调整量为10 min，航空公司B 的航班时刻平均调整量为5/3 min，所有航班时刻总调整量为35 min，平均调整量为35/6 min，方差为5.787。

表3 为双目标优化后的结果，即将方差限制在低于5.787 的范围内重新进行调整，还是以航班时刻总调整量最小为目标。经计算，航空公司A 的航班时刻平均调整量为5 min，航空公司B 的航班时刻平均调整量为25/3 min，所有航班时刻总调整量为40 min，平均调整量为20/3 min，方差为0.926。

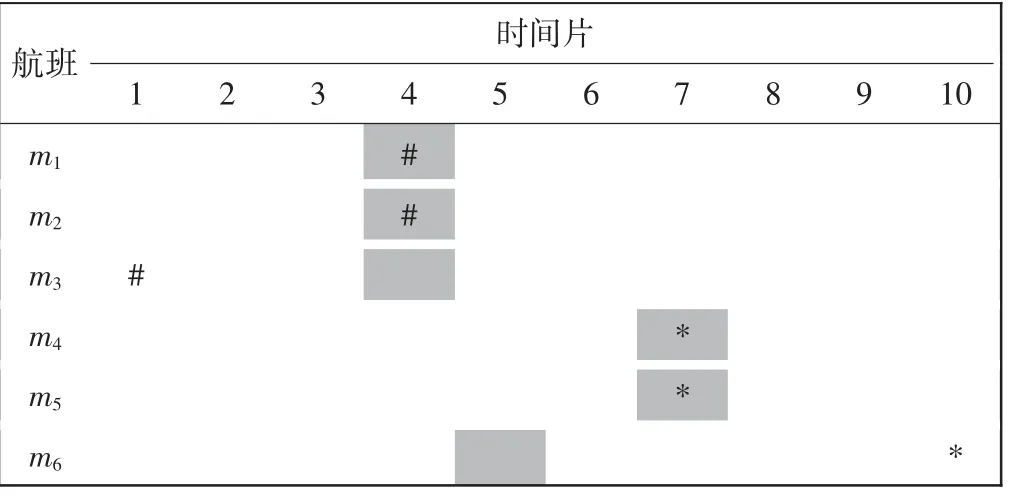
表3 双目标优化后航班调整表Tab.3 Flight adjustment table after double objective optimization

对比表2 和表3 的结果可知，当优化过程中所产生的时刻调整量由不同航空公司更加合理分配时，航班时刻总调整量是增加的，即航班时刻总调整量和航空公司时刻调整量分配的合理性是此消彼长的优化目标，需创建双目标规划模型来探究二者之间的内在关系。

2 航班时刻优化模型

2.1 参量定义

1）基本参数

模型需对航空器到达程序交叉点的时刻进行一定程度的控制，即模型对时间片的精准度要求非常高，采用5 s 为1 个时间片（模型步长），T 为时间片集合，T ＝{1，2，…，n}，t∈T。模型所用参数定义如表4 所示。

2）决策变量

3）附加变量

2.2 目标函数

（1）通过最小化机场群内航班时刻总调整量Z1，最

表4 模型所用参数定义Tab.4 Definition of model parameters

大程度减少航班时刻调配压力，即

（2）通过最小化机场群内各航空公司航班时刻调整量的方差Z2，尽量提高时刻调整量分配的合理性，即

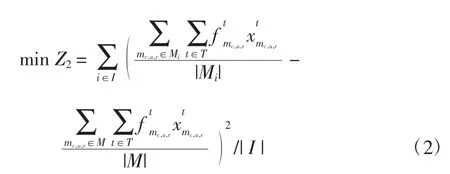
式中：|I|为机场群内所有航空公司的数量；|Mi|为航空公司i 在该机场群内所有航班的数量；|M|为机场群所有航班的数量。

2.3 约束条件

（1）一个航班一个起飞、着陆时刻，即

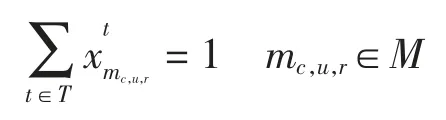
（2）一个航班一个经过航路u 的进、离港港口航路点时刻，即

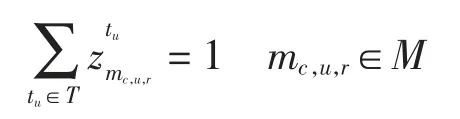
（3）一个航班一个进、离场程序，即

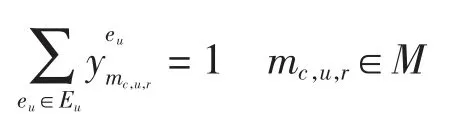
（4）一个航班经过其所选择的飞行程序上某一交叉点仅有一个时刻，即

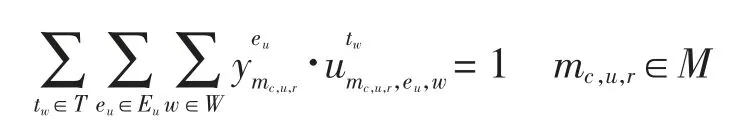
（5）为避免调整后的航班时刻脱离航空公司的实际运行情况，对航班调整时刻与原始时刻差值绝对值进行约束，即

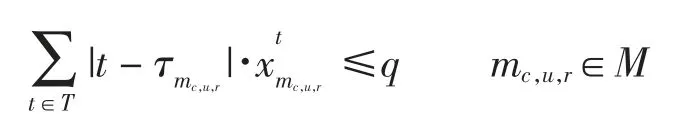
（6）机场进场、离场以及总容量约束分别表示为

式中Ts={t∈T|s≤t≤s+Δt}，s∈[0，n-Δt]。

（7）航路进港、离港港口航路点容量约束分别表示为

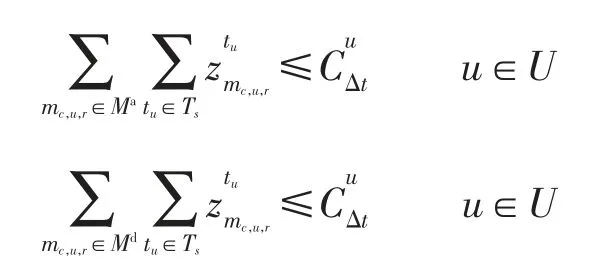
（8）过站时间约束，即

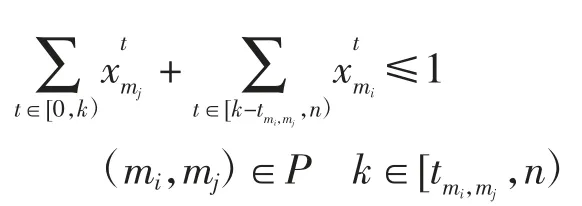
（9）着陆、起飞时刻关联性约束，即

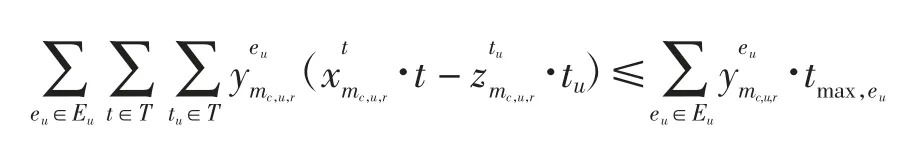
（10）程序交叉点时刻关联性约束，即

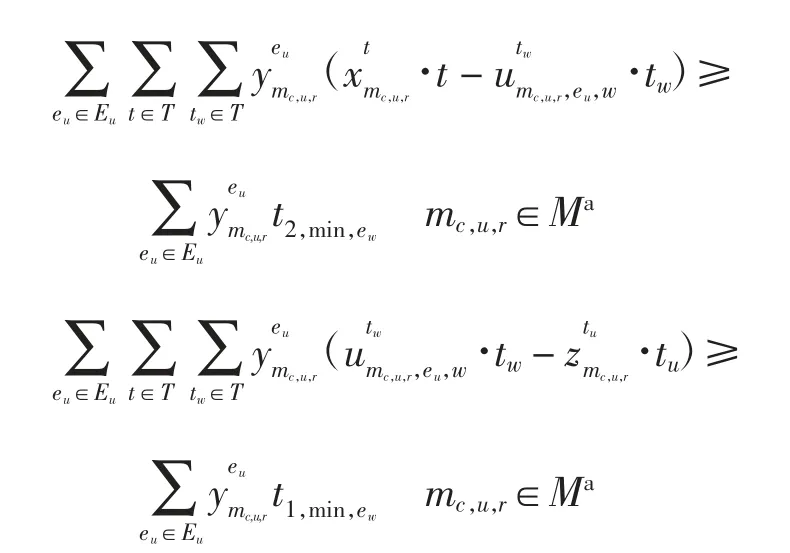
（11）程序交叉点容量约束，即

2.4 ε-约束法

为了求解该双目标0-1 整数规划问题，采用ε-约束法，其原理是将多目标问题变成单目标进行求解，将被舍弃目标的最优解作为约束条件增加在原模型中，并不断重复此过程，其模型为

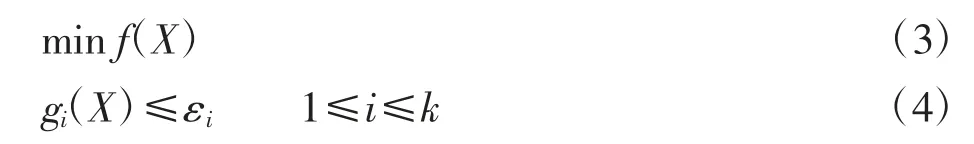
式中：f（X）和g（X）为双目标规划问题的2 个目标函数；gi（X）为g（X）的第i 次迭代；εi为gi（X）的上界。

本次双目标规划模型取g（X）= Z1，f（X）= Z2，迭代次数为5，即k=5，共产生6 个模型，依次为模型1～6。求解步骤如下。

步骤1由目标函数式（1）和约束条件（1）～（11）组成模型1 并求解，其最优解为航班时刻总调整量的最小值，即min Z1，并将此最优解代入目标函数式（2），计算结果并记为Z2（min Z1）。

步骤2由目标函数式（2）和约束条件（1）～（11）组成模型6 并求解，其最优解为航班时刻总调整量的最小值，即min Z2，并将此最优解代入目标函数式（1），计算结果并记为Z1（min Z2）。

步骤3由目标函数式（3）、约束条件（1）～（11）和式（4）组成具有新参数ε 的模型2 ～模型5。εi从模型1中minZ1开始，每次增加即εi=min Z1+迭代5 次求解一系列Z2值。

2.5 模拟退火算法

当温度为T 时，由Metropolis 准则可知粒子趋于平衡的概率为

式中：ΔE 为在温度T 时内能的改变量；K 为Boltzmann常数。由控制参数初始温度t0和初始解i 开始，重复进行“产生新解→计算目标函数差→接受或舍弃”的迭代过程，不断减小t，当算法终止时，最后的解即为近似最优解。模拟退火过程由冷却进度表控制，包括控制参数的初始温度t0及其衰减因子t、迭代次数L 和停止温度Tend。

3 实例分析

选取上海浦东国际机场（简称浦东机场）、虹桥机场和苏南硕放国际机场（简称硕放机场）2019年夏季某日17：00—20：00 时3 h的飞行计划，该时段内共起降航班415 架次，其中，浦东机场221 架次，虹桥机场142 架次，硕放机场52 架次。分析3 个机场飞行程序可知，3 个机场进场程序的主要程序交叉点有4 个，分别为JTN、PD202、PD208 和PD231。其中：JTN 为进场程序AND-61A 和PD-61A 的交汇点；PD202 为进场程序SAS-81A、SAS-82A、BK-81A 和AND-81A 的交汇点；PD208 为进场程序AND-81A、AND-82A、AND-83A、BK-81A、BK-82A 和BK-83A 的交汇点；PD231 为进场程序AND-83A、BK-83A 和DUM-82A 的交汇点。

首先，选取先来先服务原则对原始的飞行计划进行了仿真，作为原始模型；不考虑程序交叉点容量约束和时刻调整量分配的合理性，即只保留目标函数式（1）和约束条件（1）、（2）、（5）、（6）、（7）、（8）对航班时刻进行优化并仿真，作为传统模型。然后，根据上述约束法产生的模型为模型1～6。最后，应用Matlab 软件编写并运用模拟退火算法，L = 1 500，t0= 1 500，t =0.997，Tend= 0.001，分别设可接受调整量为15、30、45 min，5 s 为1 个时间片得到q∈{180，360，540}，对6 个模型依次进行求解，结果如表5 所示。

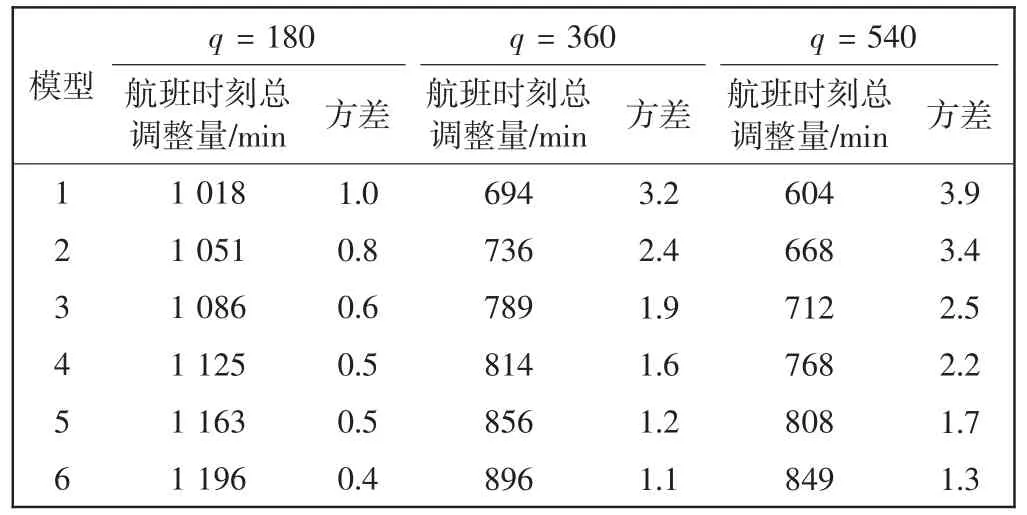
表5 不同可接受调整量的结果对比图Tab.5 Comparison of results of different acceptable time deviations

在3 种可接受调整量水平下，将6 个模型所对应航班时刻总调整量和各航空公司时刻调整量的方差进行对比。从表5 中可看出：当可接受调整量为15 min（q= 180）时，航班时刻总调整量分布区间为1 018 ～1 196 min，方差分布区间为0.4 ～1.0；当可接受调整量为30 min（q=360）时，航班时刻总调整量分布区间为694 ～896 min，方差分布区间为1.1 ～3.2；当可接受调整量为45 min（q=540）时，航班时刻总调整量分布区间为604 ～849 min，方差分布区间为1.3 ～3.9。对比可知：当q=540 时，航班时刻总调整量和各航空公司时刻调整量的方差都达到最佳；当q=360 时，航班时刻总调整量和各航空公司时刻调整量的方差都非常接近q=540 时的结果；当q=180 时，航班时刻总调整量和各航空公司时刻调整量的方差都不够理想。考虑到航空公司实际运行情况，在保证允许的最大时刻调查量不应过大的同时，尽可能减少航班时刻总调整量和各航空公司时刻调整量的方差，则将q = 360 作为约束条件（5）的最终选择。

应用AirTOP 仿真软件对长三角机场群构建空域仿真模型，将原始时刻表及q=360 所对应的6 个模型求解所得的航班时刻表导入仿真模型并运行，仿真结果如表6 所示。

表6 中，对比进场平均延误时间、离场放行正常率和管制员调配进场航班冲突次数可知，6 个模型的仿真结果都比较接近且较为理想，但考虑到各航空公司时刻调整量的方差和进场延误方差的理想程度时，模型5 和模型6 较为理想，但模型6 的航班时刻总调整量比模型5 多40 min，最终选择模型5 作为本次航班时刻优化的最终模型。

表6 AirTOP 仿真结果Tab.6 Simulation results of AirTOP

相比传统模型，模型5 的航班时刻总调整量虽增加了370 min，但可使航班进场平均延误减少24.6%，离场放行正常率基本不变，管制员单位小时调配进场航班冲突减少19 次。

4 结语

基于航空器对飞行程序的自适应选择，并对目标机场容量，进、离港港口容量和飞行程序交叉点容量进行约束，将时刻调整量合理分配到各航空公司，建立了航班时刻优化模型并采用模拟退火算法对此模型进行求解。仿真结果表明，通过增加少量的航班时刻总调整量，可大幅度降低进场航班的平均延误时间，一定程度地提高离场放行正常率，同时降低管制员调配航空器冲突的次数。该模型可为机场群和管制部门优化航班时刻提供一定的决策支持。在未来的研究中，将飞行程序与航班时刻优化结合，考虑机场群内各机场合理分配延误航班的优化方式，进一步完善航班时刻优化模型。