基于一维卷积特征与手工特征融合的集成超限学习机心跳分类方法

许越凡，肖文栋，曹征涛

1) 北京科技大学自动化学院，北京 100083 2) 北京市工业波谱成像工程技术研究中心，北京 100083 3) 北京科技大学顺德研究生院，顺德 528399 4) 空军特色医学中心，北京 100142

心律失常是由心脏电脉冲的频率、规律性、起搏位置或者传导的紊乱引起的[1]. 严重的心律失常甚至会威胁人类的生命. 心电图（Electrocardiogram,ECG）记录了人体心脏每一个心动周期所产生的电活动变化，是医生诊断心律失常的重要依据.由于心律失常种类繁多，表现复杂，识别心律失常往往需要有丰富经验的医生.而且，常规的心电图检查仅仅持续几分钟，一些偶然发生的不规则心律失常并不能被检查出来. 例如心源性猝死这种心血管病，从发病到死亡持续时间短，基于传统的常规心电图检查方式缺乏实时性，往往会耽误病人最好的治疗时间.

动态心电图监测仪（Holter），是由Norman J.Holter于1949年发明的可穿戴设备，它能够连续监测病人日常生活中24 h甚至更长时间的心脏电活动，这种长时程的记录有助于监测偶然发生的心律失常.因此，基于动态心电图的自动心律失常分类方法对于及时发现和预防心血管疾病有着重要的意义.

影响心电信号自动分类系统性能主要有两个因素，一是心电信号特征的提取，二是分类器的选择. 特征提取的质量对心跳分类性能具有至关重要的影响，提取的特征对于不同类别的心律失常应具有更好的离散性，而对同类心律失常具有相似性. 传统的心律失常分类方法使用手工提取的特征，其特征是可解释的. 之前的文献针对心电信号已经提取了各种各样的特征，包括相邻心跳时间间隔特征（RR Intervals）[2−3]、形态学特征[4]、小波特征[5−6]、高斯混合模型特征[7]和高阶统计量[8]等.对于心律失常分类任务，支持向量机[9]、k近邻[10]等分类器已经被使用.

近年来，由于自动提取特征的优势，学者们广泛研究了卷积神经网络（Convolutional neural network，CNN），提出了各种不同结构的 CNN[11−14]，并成功应用于不同领域，包括人脸识别[15−17]、语义分割[18]等.这种方法的特点是，具有原始结构的数据可直接输入到CNN中，利用CNN的逐层卷积操作，提取深层的特征，形成原始信号的抽象表示[19].

对于分类任务，往往通过在CNN网络最后一层增加softmax层实现.CNN网络参数的训练一般采用反向传播（Back propagation，BP）算法.但是，该算法容易陷入局部最优，且非常耗时.为解决上述问题，超限学习机（Extreme leaning machine，ELM）被提出.ELM是一种单隐含层前馈神经网络 （Single hidden layer feedforward neural network，SLFN），其中隐含层参数是随机生成的，不需要调整，而输出参数通过最小二乘法解析得到[20].因此，其训练速度相比于BP算法是很快的.同时，ELM具有万能逼近能力，也就是说，随着隐含层节点数的增加，网络能够以无限小的误差逼近非线性函数[21].

现有的心律失常分类方法往往只单独考虑手工提取的特征或者深度学习自动提取的特征，而融合深度卷积网络自动提取的特征和手工提取的特征对心跳信号的表示更全面，并能产生更好的分类性能.为此，本文提出了一种融合手工特征和深度特征的集成超限学习机心跳分类方法.我们设计了一种针对心跳信号分类的一维CNN结构，利用其多层卷积操作提取了心电信号的深层特征.另外又手工提取了心跳信号的特征，包括RR间期特征与小波系数特征. 然后，我们融合这些特征并将其作为ELM的输入，进行分类.为了弥补ELM随机生成参数而导致的分类结果不稳定的缺陷，我们使用Bagging方法对多个ELM分类器进行集成，得到更好的分类结果.

1 基本算法

1.1 卷积神经网络

CNN是一类包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一. 不同维度的输入数据能够用不同类型的卷积来进行操作. 二维卷积神经网络（2D CNN）由于其出色的自动特征提取功能已经成功应用于图像分类[22−23].为了同时从空间和时间维度提取特征，针对三维监控视频数据的三维卷积神经网络（3D CNN）被提出用来进行人类动作识别[24].在我们的研究中，心跳信号本质上是一维信号，为了避免从一维到二维的转换，保留数据的原始结构，我们设计了一种针对心跳信号的一维卷积神经网络（1D CNN）.

在1D CNN中，卷积层的一维卷积操作用来从局部邻域提取特征.特征映射的实现过程是由卷积核扫描其输入，然后将其结果存储到相应的特征映射的位置.卷积核大小相对于前一层的特征映射往往较小，而且卷积层会有多个卷积核，每一个都有不同的参数，这样可以提取多个局部特征，组成一系列的特征映射. 假设在第i层的第j个特征映射，在位置t的单元的值表示为，其由下式计算

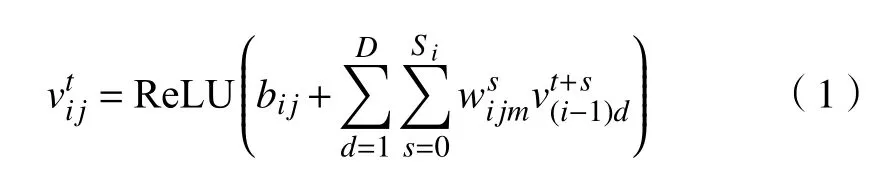
其 中 ， ReLU(·)为 线 性 整 流 单 元 （Rectified linear unit）；为对于第j个特征映射的偏置；D为第层的通道数；d为通道的序号；为第i层第j个特征映射的卷积核在位置s处的值，且该卷积核连接到第层的第m个特征映射；为卷积核的大小.

在卷积神经网络的子采样层中，特征映射的大小由对上一个卷积层的特征映射的局部邻域进行池化而减少.CNN结构通过多个卷积和子采样堆叠而成.

1.2 超限学习机

ELM是一个具有单隐含层的前馈神经网络，它包含输入层、隐含层、输出层共三层，其基本结构如图1所示. ELM隐含层参数是随机生成的，输出层参数基于最小二乘法解析得到.这种训练方式是免迭代的，避免了常规反向传播训练会陷入局部最优的缺点. 黄广斌等[21]证明了ELM具有万能逼近能力. 具体地，给定任何有界非常数的分段连续激活函数，一个隐含层参数随机生成的网络，仅仅通过调整其输出参数就能够以任意小的误差逼近目标函数.

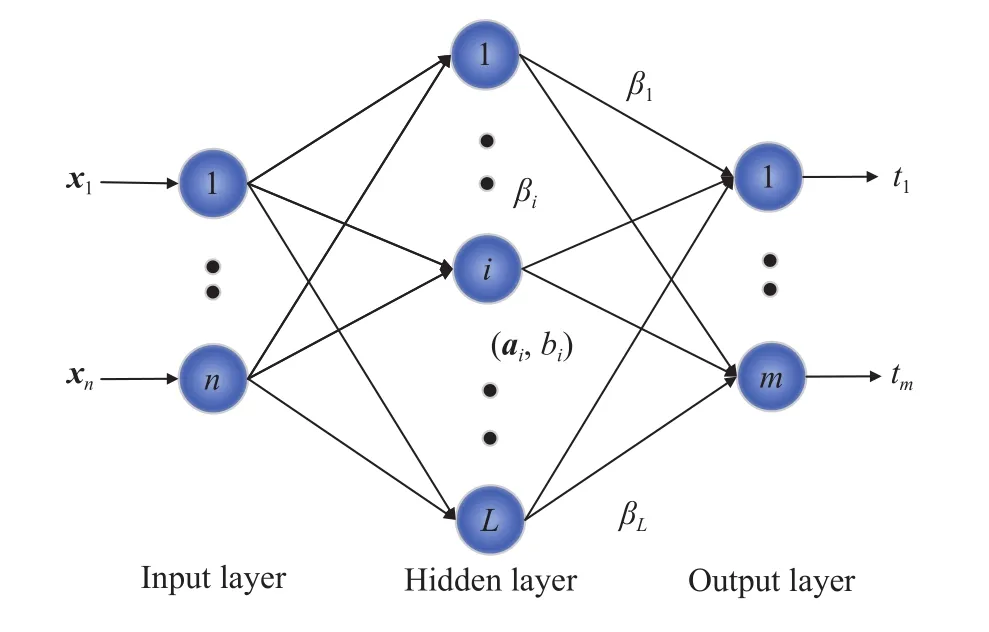
图1 ELM的基本结构Fig.1 Basic structure of an extreme learning machine (ELM)

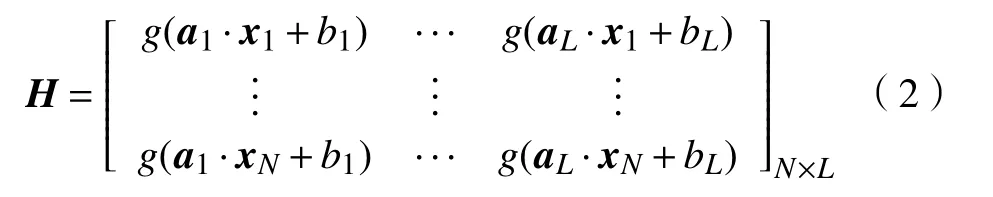
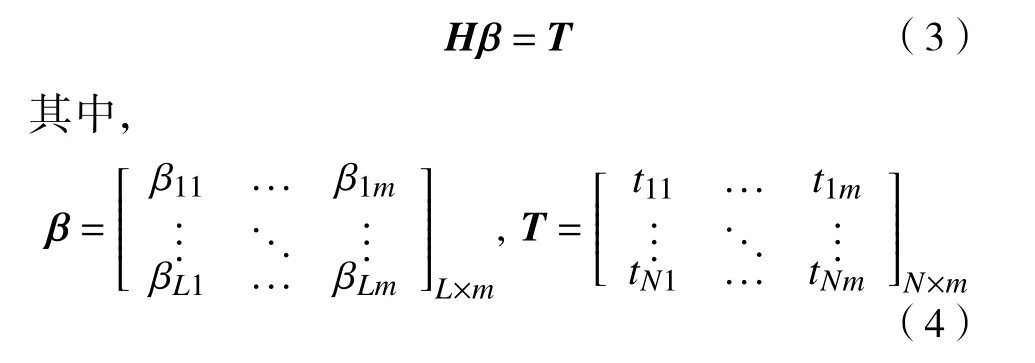
在实际中训练数据的数量与隐含层节点数量往往不相等，也就是说，隐含层输出矩阵H并不是一个方阵，因此等式（3）的最小二乘解不唯一.Bartlett指出，对于前馈神经网络，网络权重越小，该网络的泛化性能越好[25].因此，输出参数的最小范数的最小二乘解为

2 提出的方法

本节将对所提出的特征融合集成ELM心跳分类方法进行详细论述.

命题1：由制造商主导的Stackelberg博弈情形下， 当 4kα-θ2＞0， 且 D-k（Cm＋Cs）≥0 时， 具有如下的最优均衡解：

2.1 总体结构

图2展示了所提方法的总体结构，总共包括4个阶段，分别为ECG信号预处理、心跳分割、特征提取和心跳分类. 在预处理阶段消除了ECG信号的基线漂移. 在心跳分割阶段将连续的ECG信号分割为单个的心跳片段. 特征提取阶段分为手工特征提取和深度特征提取.手工特征包括时域特征以及时频特征.同时使用1D CNN自动提取心跳信号的深度特征.我们融合手工提取的特征和深度特征，将其作为一个心跳信号的新的特征表示.在心跳分类阶段，为了提升ELM分类性能的稳定性，采用Bagging集成方法组合多个ELM分类器，最后以多数投票的方式得到最终的分类结果.

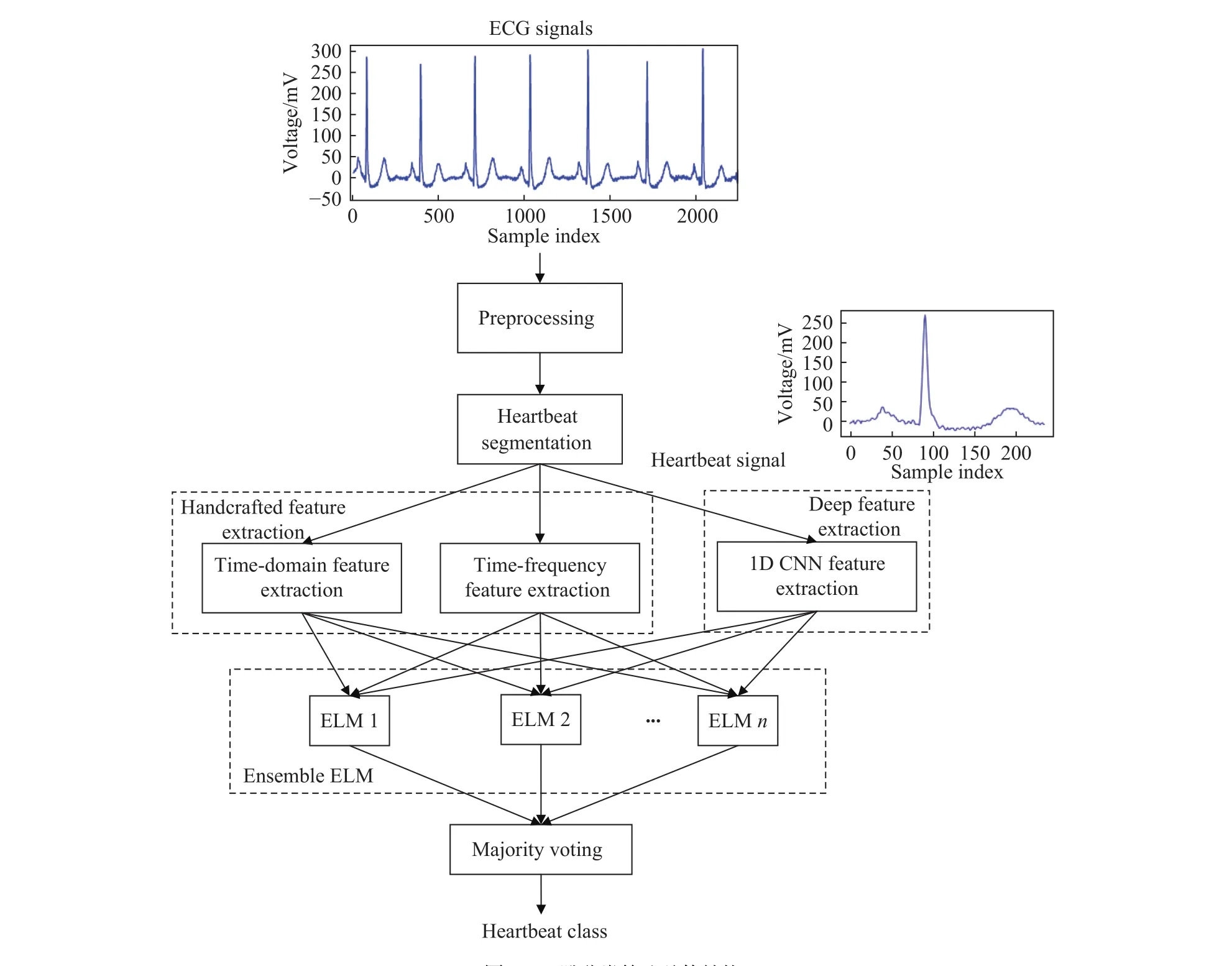
图2 心跳分类算法总体结构Fig.2 Overall structure of the heartbeat classification algorithm

2.2 手工特征提取

2.2.1 RR间期特征提取

RR间期特征反应了心跳在时间域的特性.总共4类RR间期信息被计算：前RR，即当前心跳与前一个心跳的R峰的时间间隔；后RR，即当前心跳与后一个心跳的R峰的时间间隔；短期RR间期，当前心跳的前十个RR间期的平均值；长期RR间期，当前心跳的前五分钟RR间期的平均值.

2.2.2 时频特征提取

小波变换是一种时间−频率分析方法，它具有多分辨分析的特点，而且在时频两域都具有表征信号局部特征的能力.因此，适合于分析非平稳的信号和提取信号的局部特征.离散小波变换（Discrete wavelet transform，DWT）是小波变换的一种，它是将尺度参数和平移参数离散化.在本文中，我们使用DWT作为特征提取器，提取心跳信号的局部特征.小波类型选择Daubechies 1小波，小波分解层数为五层.小波分解第五层的近似系数和细节系数被用来作为一个心跳片段的时频特征.

2.3 一维卷积神经网络

在图像分类中，由于图像中蕴含的模式较为复杂，2D CNN往往需要较深的结构.而对于ECG信号，其网络的输入是分割后的心跳片段，维度较低.采用过深的网络结构可能会恶化分类性能且增加计算代价.因此，我们设计了一个具有较浅结构的1D CNN，总共有7层，如图3所示. 模型包括三个卷积层，两个子采样层，一个全连接层和一个输出层.C1是一个卷积层，包括30个特征映射.每个核的长度是15，连接到输入信号的相邻15个样本点.S2是一个子采样层，由执行在C1层特征映射上的最大池化操作得到.C3也是一个卷积层，包括10个特征映射.每个核的长度为4.S4是子采样层，由执行在C3层特征映射上的最大池化操作得到.随后所有S4层的特征平铺成一个350维的特征向量，C5层的特征作为对输入心跳信号的深层特征表示. 全连接层F6以及输出层共同执行分类任务. 输出层的神经元个数与待分类的心跳信号类别数量一致，即16个输出层神经元.

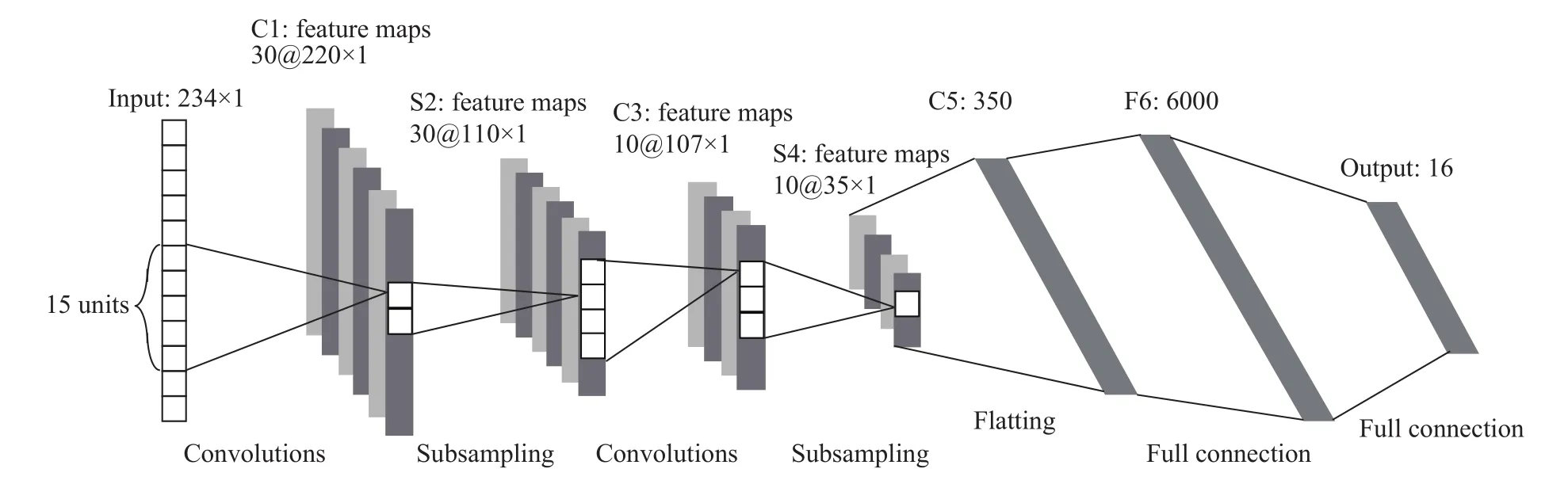
图3 本文提出的1D CNN结构Fig.3 Structure of the proposed 1D convolutional neural network

损失函数选用交叉熵（Cross entropy）.随机梯度下降用来训练神经网络的参数. 使用三种提升权重训练过程的方法，分别为：权值衰减（Weight decay）、动量（Momentum）和随机失活（Dropout）.权值衰减就是在权重更新规则中加入一个项使得权值指数地衰减到0，这个方法可以用来避免过拟合. Momentum是一种加速梯度下降的技术，对于那些当前的梯度方向与上一次梯度方向相同的参数进行加强，即在这些方向上更快；相反，对于那些当前的梯度方向与上一次梯度方向不同的参数进行减弱，即在这些方向上减慢.Dropout是指在每次训练迭代中，随机地从神经网络中消除一部分节点，这也是一种避免过拟合的技术.

2.4 ELM 心跳分类

当手工特征和1D CNN的深度特征被提取出来后，它们被整合到一起作为ELM的输入.图4显示了基于单个ELM的心跳分类模型.其中，输入层是由手工特征包括RR间期特征和离散小波系数特征以及深度特征即1D CNN特征共同组成，因此ELM输入层节点数等于所有这些特征的总个数. 输出层节点数等于待分类的心跳类别数.

图4 ELM心跳分类结构Fig.4 ELM heartbeat classification structure

2.5 Bagging 集成方法

当多个不同的训练集被构造出来后，分别在这些训练集上训练不同的ELM心跳分类模型. 最后通过多数投票的方式，票数最多的心跳类别即为最终集成的分类结果.

3 实验验证

本文中使用麻省理工律失常公开数据集（MIT−BIH arrhythmia dataset）对所提出的方法进行验证.

3.1 数据集

MIT−BIH心律失常数据库是研究心律失常分类算法广泛使用的数据库之一[26]. 它包含48个0.5 h的双通道动态心电图记录，其中的23份为比较常见的心律失常记录，而其余的25份为较少见但临床意义重大的心律失常记录[27].这些记录来自于BIH心律失常实验室在1975年至1979年间研究的47名受试者，从波士顿贝斯以色列医院住院病人（约60%）和门诊病人（约40%）的混合人群中收集得到.

在通道一，45条记录来自改进的肢体导联II（Modified limb lead II，MLII），其余 3条记录来自改进的胸前导联V5（Modified precordial lead V5）.在通道二，40条记录来自导联V1，4条来自导联V2，1条来自V4，2条来自V5，还有一条来自MLII.本文中，我们使用通道一的数据，因为通道一的数据都来自于导联MLII.

这些记录被带通滤波到0.1～100 Hz的频率范围，然后将带通滤波后的信号数字化到360 Hz. 所有的ECG信号使用两个中值滤波器来消除基线漂移，分别是0.2 s宽度的中值滤波器和0.6 s宽度的中值滤波器.

MIT−BIH数据库中提供了大概的R峰基准点的位置.我们使用提供的基准点位置，然后对其进行了手工纠正.接下来，根据基准点的位置，前90个点和后144个点总共234个点组成的片段，作为一个心跳片段.在数据库中心跳数据的真实标签是由两个心脏病专家手工标注得到，因此我们使用提供的标签作为心跳的真实标签.在我们的实验中，所有48条记录被使用，总共将心跳信号分为16类.

表1详细的描述了数据集的情况.我们的实验中，数据集的划分和文献[9]中保持一致. 具体来说，将N类样本的13%，L、R、A、V、P类各类样本的40%以及其余的心律失常类样本的50%从各自的样本中随机选择出来，然后组成了训练样本，剩余的样本组成了测试样本.

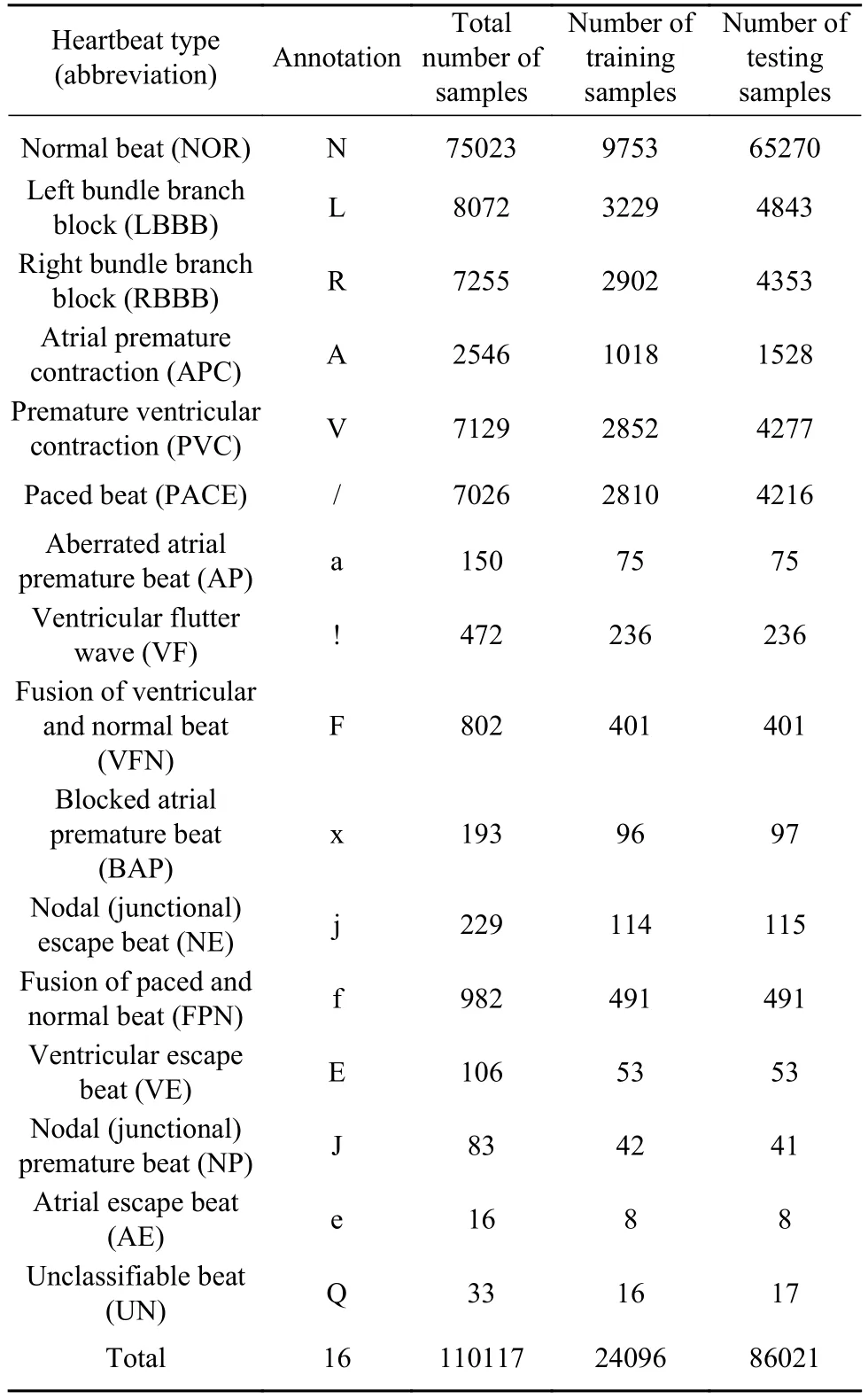
表1 MIT−BIH数据集的详细描述和划分Table 1 Detailed description and division of the MIT−BIH dataset

3.2 性能指标

为了评价心跳分类方法的性能，我们使用以下三个指标，分别为：准确率（Accuracy），召回率（Recall）和精确率(Precision). 其中，准确率反映了模型预测正确的样本占所有样本的比例，召回率反映了在真实类为正类的样本中，模型识别为正类样本所占的比例，精确率反映了在模型识别为正类的所有样本中，真实类也为正类样本所占的比例. 它们的计算方法如下：

其中，TP、TN、FN和FP分别为真阳性数（True positive）、真阴性数（True negative）、假阴性数（False negative）和假阳性数（False positive）.

3.3 实验结果

实验统一采用五折交叉验证的方式进行模型效果评估.抽样的方式选择分层抽样，也就是说，在训练集中，我们对于每一类心跳分别将其平均分为五份，将每一类中的每一份样本进行组合，形成五份样本子集.轮流选取其中的四份作为训练集，一份作为验证集.重复训练及验证模型五次，并将五次结果的平均准确率作为模型选择的评价标准.

表2中给出了每一个心跳类别的召回率和精确率. 大部分类别呈现出了满意的分类性能，除了类别a、F、e和Q.表3给出了分类结果的混淆矩阵（Confusion matrix），从中我们可以观察到具体的分类情况. 具体地，在真实类别为a类的所有样本中，26个被误分，主要为11个样本被误分为N，4个被误分为A，还有7个被误分为V，其原因是类别a与其他3个误分类别的形态学差异并不明显；82个F类样本被误分，主要为54个F类样本被误分为N类，27个被误分为V类，原因在于MIT−BIH数据集编号为213的记录中，F类样本和N、V类样本具有很强的形态学相似性，这就导致F类很容易被错误地识别为N和V类；在所有8个e类样本中仅仅分对了1例，而其他都被误分为N类，这也是归因于在MIT−BIH数据集编号为223的记录中，e类心跳信号与N类的形态学特征并没有明显的区别；Q类的心跳信号表现为无规则地而且幅值变化很大的震荡，心血管专家将这类样本标注为未分类样本，因此如何减少这类样本的信号变形和损失是关键，但这不在本文研究的范围内.

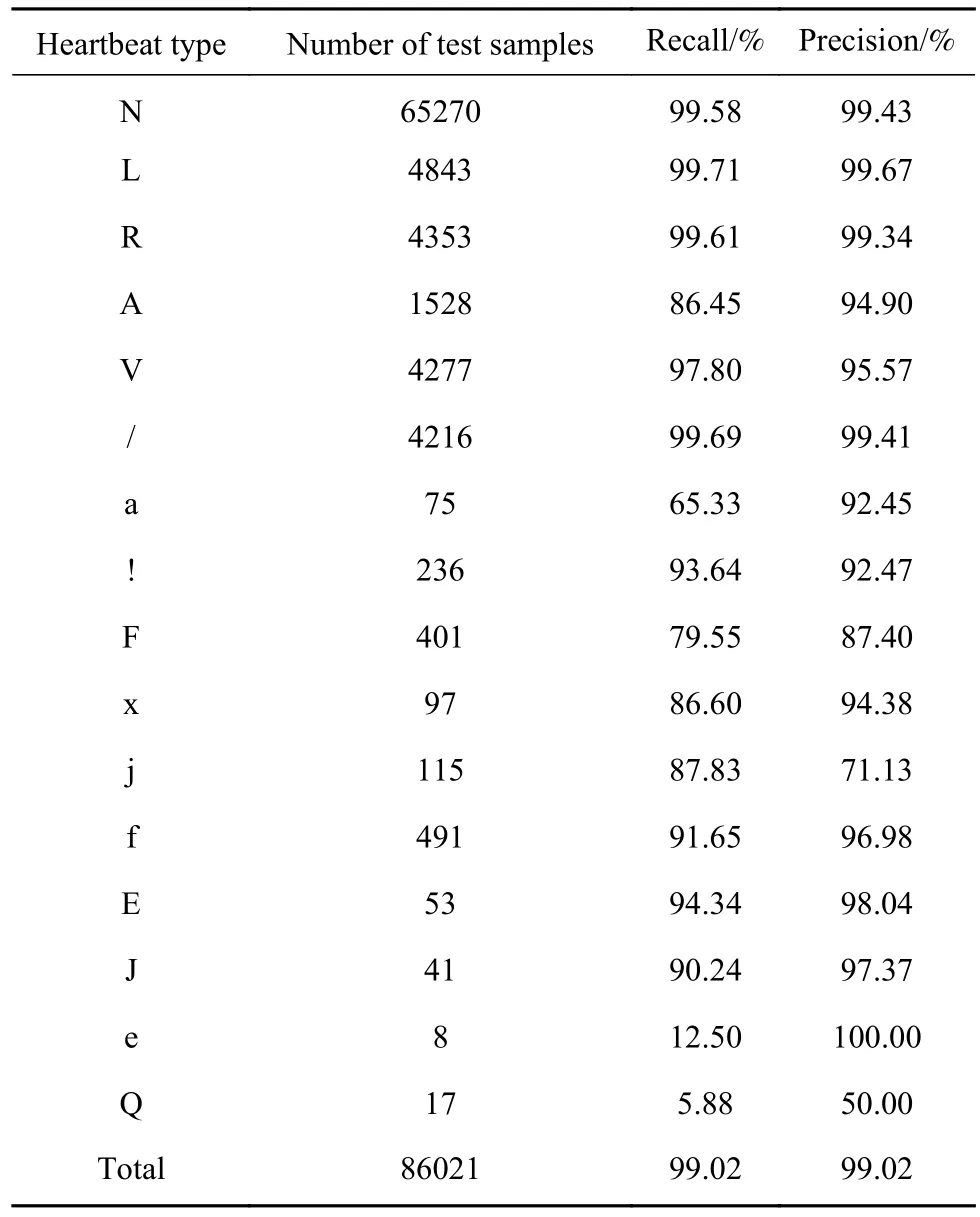
表2 每类心跳的召回率和精确率Table 2 Recall and precision for each heartbeat class

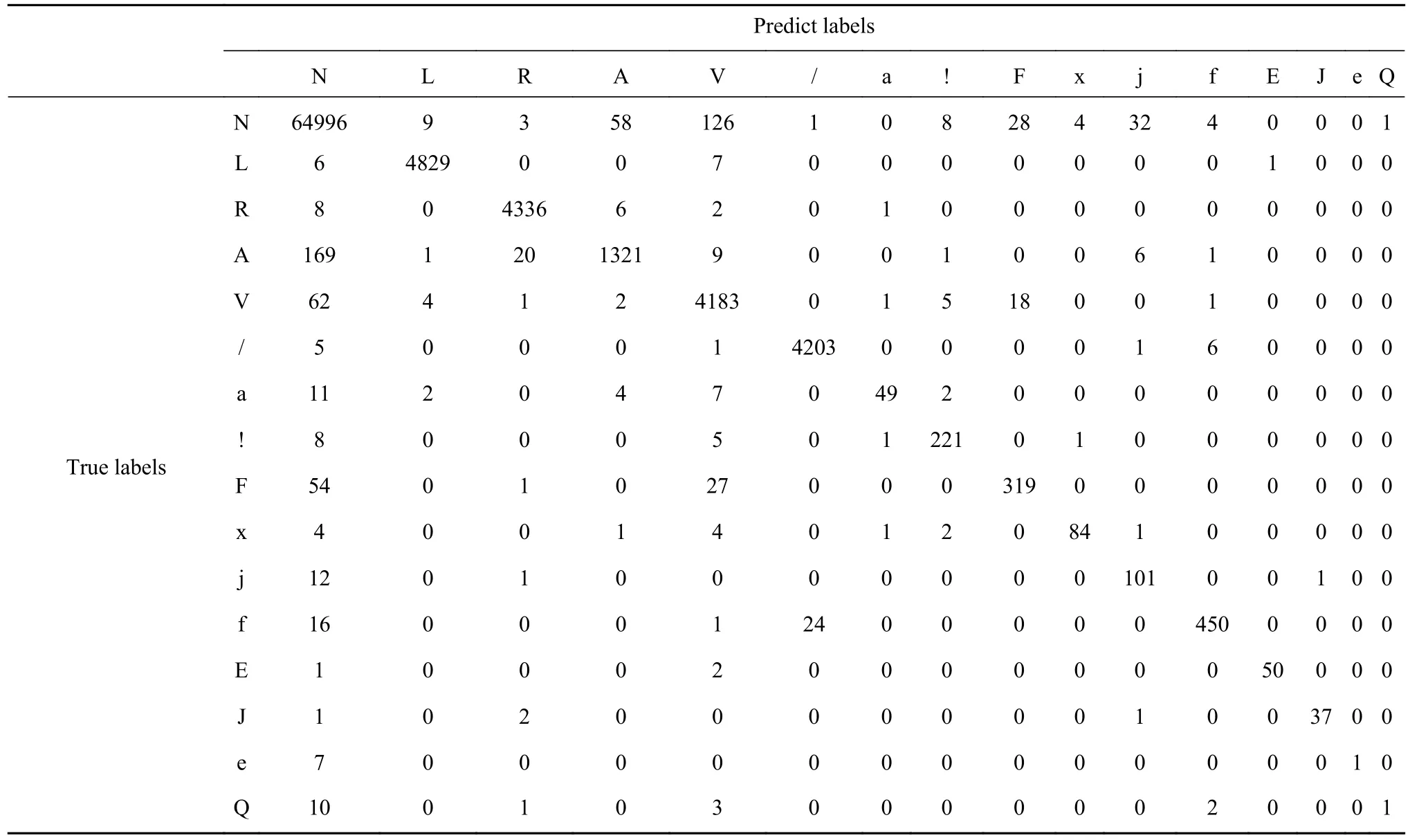
表3 混淆矩阵Table 3 Confusion matrix

表4展示了所提方法与其他方法的比较结果.基于融合特征的ELM算法在单导联的准确率为98.81%，比文献[9]中方法得到的98.72%准确率更高. 而且，基于融合特征的分类方法其效果要好于单独用手工特征或深度特征的方法.另外，基于Bagging集成的ELM分类方法进一步提升了分类性能，达到了99.02%的最高准确率.

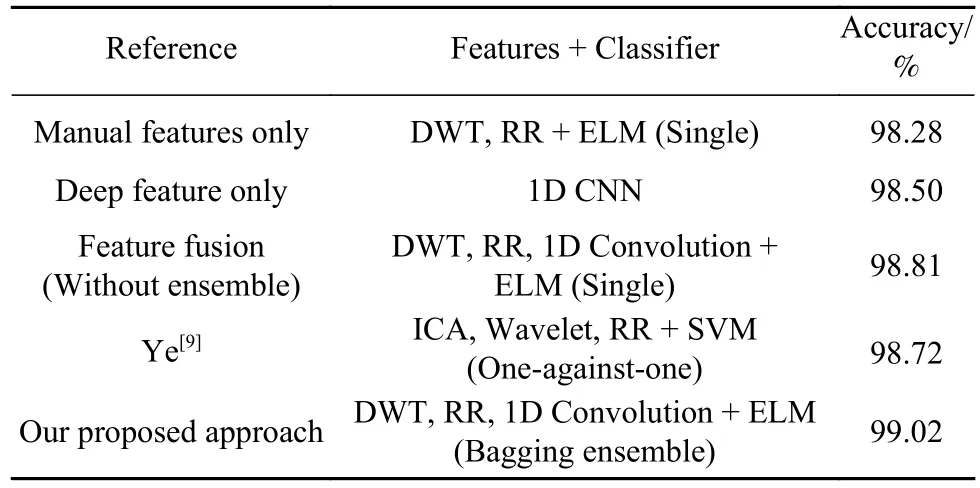
表4 提出的方法与其他方法的比较结果Table 4 Comparison results of the proposed approach with other approaches

4 结论

本文提出了一种基于手工特征和深度特征融合的集成超限学习机心跳分类方法.手工提取的特征包括RR间期特征和离散小波系数特征，分别反映了心跳信号的时域特性和时频特性.同时设计了针对心跳信号的1D CNN结构，对心跳信号的深度特征进行自动提取. ELM模型融合上述特征并进行心跳分类.由于ELM初始参数随机生成，这种方式会导致ELM出现分类性能不稳定的现象，因此，针对上述问题，本文采用基于Bagging策略的多ELM集成方法.实验结果表明，将深度特征与手工特征融合能更全面地表征心跳信号，并得到更好的分类结果. 此外，基于Bagging策略的ELM集成方法可进一步提升心跳分类性能. 未来工作将基于其他公开的心律失常数据集，对所提出的方法加以改进.同时，将所提方法应用到临床实践中.