双闭合载流回路互感能量的三种计算方法
2018-10-26刘顺攀
朱 峰, 刘顺攀
(西南交通大学 电气工程学院, 四川 成都 610031)
0 引言
与静电场一样,恒定磁场中也储存有能量。这些能量是在磁场形成的过程中,由外源提供的其它形式的能量做功转化而来的[1]。若空间中存在两个或更多的电流回路,其电流变化使穿过回路的磁通发生变化并在不同的回路中相互影响,产生电流回路之间的相互作用能。它与各回路电流及互感系数M有关,称为互有能。
若线性媒质中有两个回路l1、l2,在两个回路中的电流从0分别增加到l1,l2的过程中,外源对回路所做的功都转变成磁场中所储存的能量Wm,有:

(1)
式中,n表示在此系统中的回路个数,ψ1和ψ2分别表示穿过l1,l2回路的磁链,有:
(2)
将磁链表达式带入能量计算式得:
(3)

在各类电磁波与电磁场的教材中,对于互感能量MI2I2的结论,往往仅从一个角度去计算和推导,使学生理解互感能量的实际产生过程存在一定难度。
本文将阐述三种计算两个电流回路间互感能量的计算方法。
1 对充电过程积分计算互感能量
1.1 对单一回路的充电过程计算互感能量
在两个电流回路l1、l2构成的磁场系统中,为方便计算互感能量,可将其中回路l1的电流固定为l1,仅对另一回路l2的电流从增加到l2的充电过程进行分析,以求解其互感能量。

将l1、l2的充电过程所产生的互感能量分别讨论,在回路l1充电时,在两个回路中均未产生互感能量。回路l1充电完成后,令回路l1的电流保持不变,回路l2的电流从0增加到I2的过程中,在时间dt内,回路l2对回路l1引起的磁通改变量为
dψ12=M·di2
(4)
在回路l1中产生的感应电动势为
(5)
由于在回路l2充电的过程中,穿过其回路自身的磁通也穿过了回路l1,故回路l2的电流变化也会导致回路l1中产生相应的感应电动势,产生的感应电动势方向与回路l2磁通变化的方向有关,故此过程中回路一要维持电流I1不变,外源可能吸收或释放能量[3]。
外源做功(或吸收能量)的微元为
dW=-ε12·I1dt
(6)
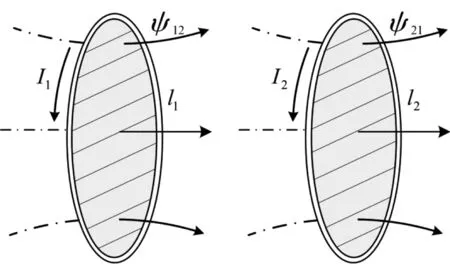
图1 线圈互感示意图
在此过程中,外源所做总功为

(7)
可得:

(8)
由于回路l1中电流没有变化,故回路l2磁通并未受到回路l1电流影响,即回路l2中没有产生互感能量。则回路一中的互感能量为
W12=W=MI1I2
(9)
回路2中的互感能量:
W21=0
(10)
两回路磁场系统中储存的互感能量为
W12+W21=MI1I2
(11)
1.2 对充电过程积分计算互感能量
在1.1节中,已经讨论了关于两个电流回路异步充电的互感能量计算过程。若不固定任何一回路的电流,将两回路电流建立为两个关于时间的函数表达式i1(t)和i2(t)可得,两回路的磁通ψ(t),感应电动势ε(t),l1、l2中产生的互感能量W12(t)和W21(t),均是关于时间的t函数。
若当t>T时,回路l1、l2中的电流均不再变化,在0 图2 线圈同步充电互感示意图 回路l2电流变化对回路l1产生的磁通的影响为: dψ12(t)=M·di2(t) (13) 回路l1中产生的互感感应电动势为 (14) 回路l1的电源提供的互感能量等于回路l1中增加的互感能量: dW12(t)=-ε12(t)·i(t)dt=M·i1(t)di2(t) (15) 由能量守恒得,在t=0到t=T的过程中,回路l1中外电源做功即为互感能量的增量,为 (16) (17) 在上式中,当时t≥T时,i1(t)=I1,i2(t)=I2,即T表示两个电流回路均完成充电的时间点,则有: (18) 又因为: (19) 其中,W21恰好为回路l1的电流变化对回路l2电流的影响过程中,回路l2外源所做功, W12=MI1I2-W21 (20) 则有,两回路均充电完成后,两回路产生的互感能量之和为: W21+W21=MI1I2, (t≥T) (21) 对于线圈法向互相垂直的两恒定电流回路l1和l2,如图3所示: 图3 线圈回路旋转初始状态 两回路产生的磁场互不交链(假设两线圈间的距离足够长),此时的互感能量为0,两线圈回路之间作用力为0,且处于临界平衡状态,若此时给回路l2一个微小的力,同时固定住回路l1,则由于磁场力的作用,回路l2会发生绕轴AA′的顺时针方向的转动[2,3]。此时回路l2的磁距为 m2=I2·S2 (22) 其所受回路l1的磁场产生的力矩为[1] (23) 其中,α表示回路l2的法线方向与回路l1产生磁场的方向夹角,T21<0表示力矩企图使广义坐标α减小。在两回路内的电流保持不变时,外源提供的能量,有一半作为磁场能量的增量,另一半用于作机械功[1]。对力矩T21积分可得回路转动所需的机械能量WF,此能量在数值上等于在新的磁场建立时系统的相互作用能W21,故: (24) 回路旋转完毕后,回路l2共旋转了90°,此时两线圈回路的相互作用力再次变为0,且处于平衡状态,假设线圈回路的转动速度极其缓慢,其转动角度不会超过90°[4],则: (25) 图4 线圈回路旋转完毕 又因为: (26) W21=I2ψ21=MI1I2 (27) 由于在整个回路转动的过程中,始终只有回路l2在转动,故: W21=MI1I2,W12=0 (28) W12+W21=MI1I2 (29) 综上所述,两回路中的磁场增量为MI1I2。 互感与互感能量的计算是电磁场和电气工程领域中重要的参数计算,在实际工程领域中,互感能量和自感能量均是与时间或空间位置相关的过程量。本文基于功能关系,从三种不同的角度,通过对充电过程积分和对广义力矩积分的方式,分别从时间和空间上对于不同电磁环境的电流回路系统的互感能量进行了计算和证明,均得到与现有教材中列出公式一致的结论。本文相对简单的数学证明和对互感能量形象的诠释,对现有教材是极大的补充,降低了此知识点的理解难度,使学生更容易接受互感能量计算公式的由来,并对其在空间中的存在方式有更深的理解。

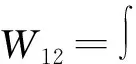


2 广义力矩积分求互感能量






3 结语
