外加直流电场条件下熔渣电场分布的数值模拟
2021-09-25顾鹏伟许继芳1张捷宇
胡 旭 顾鹏伟 许继芳1, 张捷宇
(1.上海大学省部共建高品质特殊钢冶金与制备国家重点实验室,上海 200444;2.上海大学材料科学与工程学院,上海 200444;3.苏州大学沙钢钢铁学院,江苏苏州 215000)
近几十年来,冶金行业在保持经济竞争力的同时,也迎来全新的挑战——环境和社会效益要求的日益提高[1-3],为此涌现出大量全新的冶金方法和理论,如外加电场、磁场和超声波等技术[4]。其中外加直流电场冶金技术因其独特的焦耳热效应和电迁移效应而广泛应用于直流电渣冶金、熔融氧化物电解、金属凝固等过程[5]。李建朝等[6]通过在钢液与Al2O3-CaO-MgO熔渣体系间施加稳定的直流电场,并进行钢液脱氧试验,发现该方法能有效脱除钢液中的溶解氧。李万锋等[7]研究发现,直流电场作用改变了K417G镍基高温合金凝固组织中枝晶的生长形态和碳化物的形貌,并引起凝固组织择优生长取向的变化及第二相分布和形态的变化。外加直流电场冶金技术利用直流电场力和焦耳热效应等来实现对冶金过程中能量传输、流体运动和形状的控制,从而达到优化冶金过程、提高生产效率、改善产品质量和提高产品性能的目的[8-9]。
冶金反应具有电化学本质,在熔融状态下熔渣中的CaO、MgO和FeO等离子化合物大部分解离为离子状态[10]。在电场作用下,电场力通过对熔渣中的离子起作用,从而影响熔渣的流动和分布,进而影响熔渣冶金效果。通过改变电场条件可有效改善熔渣的冶金性能,达到调控钢液的目的[11]。熔渣中电场的分布对电场作用效果有一定影响,因此有必要研究不同电场条件下熔渣中的电场分布规律。目前,研究者对熔渣外加直流电场已经进行了较多研究[12-15],并且在某些参数对熔渣电场分布影响方面取得了一定的进展。由于高温环境下熔渣难以观察且电场难以观测,使得电场下高温熔渣性质的试验研究相对困难,因此迫切需要一种能够模拟电场对熔渣冶金性能影响的模型。基于此,本文运用COMSOL数值模拟软件建立了熔渣外加直流电场模型,研究了电压、电极直径和插入深度、熔渣介电常数等参数对电场分布的影响,探究了外加直流电场条件下影响熔渣电场分布的因素,以期为优化熔渣外加直流电场参数提供数据支撑。
1 模型的建立
采用COMSOL数值模拟软件中的AC/DC模块模拟熔渣的电场分布[16-17]。为了方便研究电压、电极直径和插入深度、熔渣介电常数等参数对熔渣电场分布的影响,将模型简化为坩埚外加电场模型,如图1所示,主要包括坩埚、熔渣和电极3部分,坩埚中盛有熔渣,阳极插入熔渣,阴极设在熔渣底部。电场参数如表1所示,其中电极直径以无量纲数D/D0(D为电极直径,D0为熔渣横截面直径52 mm)表示,电极插入深度以无量纲数H/H0(H为电极插入深度,H0为熔渣高度94 mm)表示。
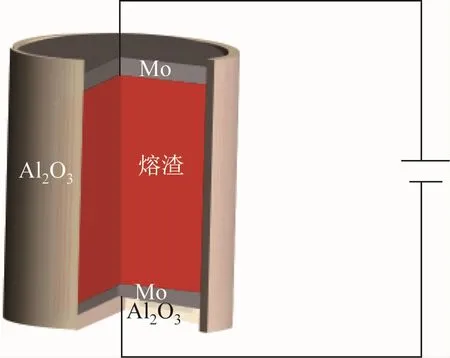
图1 熔渣外加电场模型视图Fig.1 Section view of the model of the slag in applied electric field
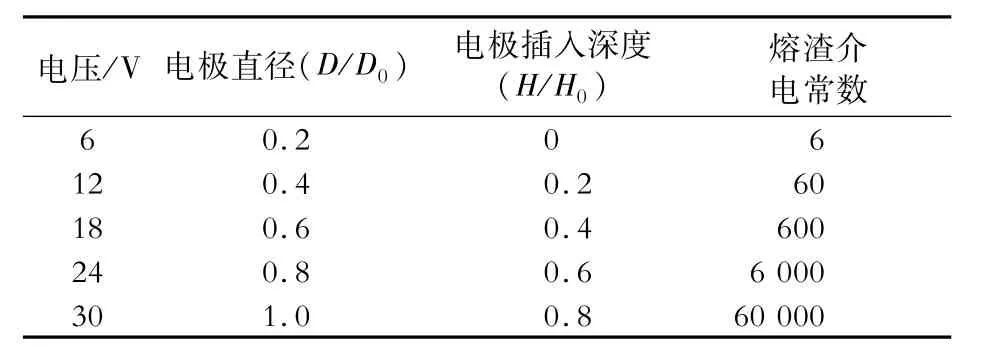
表1 电场参数Table 1 Electric field parameters
为了最大程度保证模拟结果的可靠性,根据试验装置实际尺寸与材料建立有限元模型,具体尺寸与材料如表2所示。并根据各部分模型材料的参数设定材料属性,其中熔渣材料成分(质量分数)设置为40% CaO-50% Al2O3-5% MgO-5% FeO,坩埚材料设置为Al2O3,电极材料设置为钼金属,如图2所示。设置电场边界条件和初始条件:熔渣在电场中定义为各向同性的材料,其相对介电常数为6[14];由于Al2O3坩埚不导电,因此将电场设为零电荷;对上下对应的两钼电极施加大小相同而方向相反的电压。采用COMSOL软件的极细化方式对整个模型进行网格剖分,结果如图3所示,其中模型最大单元格尺寸为2 mm,最小单元格尺寸为0.02 mm,网格总数约828 415。为了便于模拟计算,提出了几点假设:(1)该研究是基于系统稳定工作状态下进行的;(2)坩埚和电极均为等势体;(3)坩埚不导电,电流全部通过两极;(4)电场分布相对均匀,相对于熔渣中心呈对称分布;5)熔渣的电阻率为常数。

图2 材料属性设置示意Fig.2 Schematic diagrams of setting material property

图3 模型网格剖分示意Fig.3 Schematic diagram of grid subdivision model

表2 材料规格参数的设定Table 2 Setting of material specification parameters
2 模拟结果及分析
2.1 模型验证
不同电极直径下熔渣电场线分布的模拟结果如图4所示,图中箭头与流线表示电场线,标尺表示两极之间的电压差。由图4可以看出:当D/D0=1时,熔渣中的电场线均由正极射向负极,两极之间的电压差由大变小,电场线均为直线,电场线的方向与电场强度的方向相同,因此场强的方向也由正极指向负极;当D/D0=0.2时,即电极面积小于熔渣截面积时,电极附近电场线集聚,说明此处电场强度较大,而远离电极处电场线比较稀疏,说明该处电场强度较小。两个电极之间的电场线分布比较规律,各部分电势比较稳定。上述模拟结果符合电场线的分布规律,表明用该模型模拟外加直流电场条件下熔渣的电场线分布是可行的。
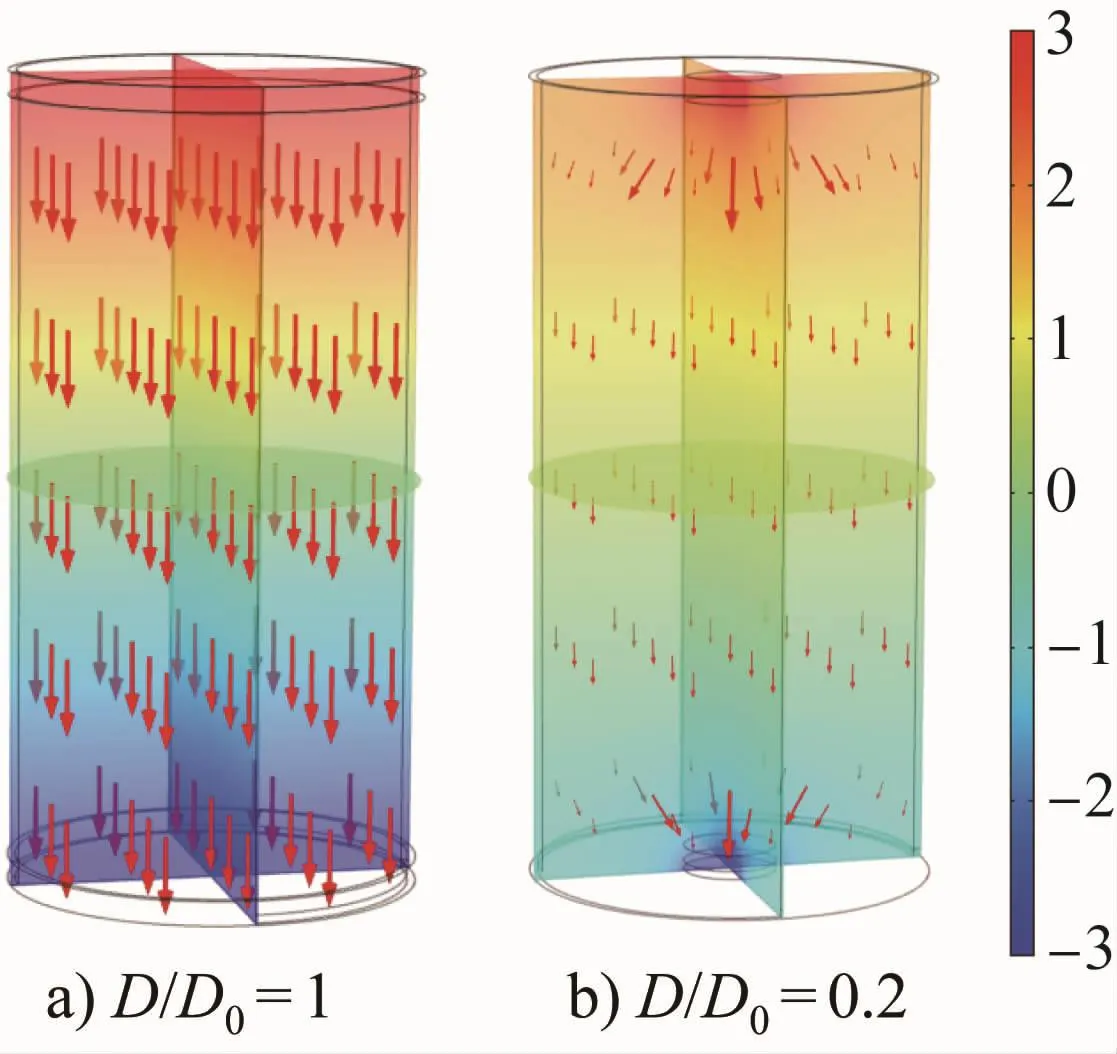
图4 不同电极直径下熔渣的电场线分布(电压6 V,H/H0=0,熔渣介电常数6)Fig.4 Distributions of electric field lines in slag with different diameters of electrode(voltage of 6 V,H/H0=0 and slag permittivity of 6)
2.2 电压的影响
电压是生产过程中相对容易改变的参数,在其他参数不变的条件下,系统内的电流大小由外加电压控制,而电流大小对熔渣电场分布有明显影响。图5为6、12、18、24、30 V电压下熔渣电场线分布,很难根据电场线疏密看出电场强度的强弱,但可根据匀强电场公式进行判断,公式为:

图5 不同电压下熔渣的电场线分布(D/D0=1,H/H0=0,熔渣介电常数6)Fig.5 Distributions of electric field lines in slag under different voltages(D/D0=1,H/H0=0 and slag permittivity of 6)

式中:E为电场强度;U为外加电压;d为两电极之间的距离。
在阳极和阴极间距不变的条件下,电场强度随外加电压的增加而线性增大,提高外加电压是提高系统电场强度的有效手段。由于电场强度是矢量,无法直接比较大小,因此采用电场能量衡量电场强度的强弱。根据电容器的定义,一个导体发出的电场线全部终止在另一个导体的导体系称为电容器,该模型符合电容器的定义,因此可将其看作一个简单的电容器。根据电容器的电场能量表达式计算该模型系统的电场能量,计算公式为:
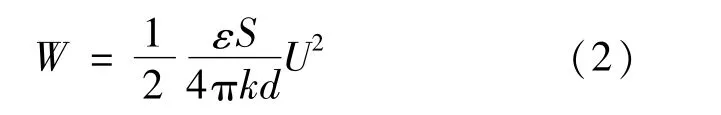
式中:W为电场能量;k为静电力常量;S为电容板的面积;ε为电容板中间材料的介电常数。
由式(2)计算得到系统电场能量随电压的变化如图6所示。6可以看出,在其他电场参数不变的条件下,电场能量随电压的增加而增加。提高外加电压是提升系统电场能量的途径之一。
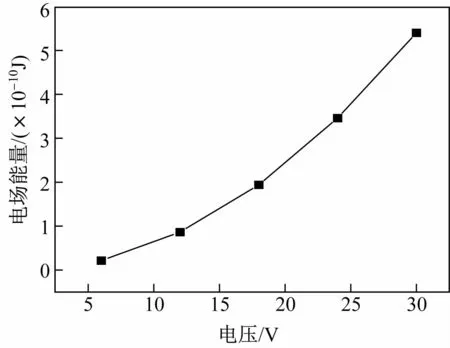
图6 电场能量随电压的变化(D/D0=1,H/H0=0,熔渣介电常数6)Fig.6 Electric field energy versus voltage(D/D0=1,H/H0=0 and slag permittivity of 6)
2.3 电极直径的影响
电极直径也是一个容易控制的变量,该值的大小直接影响熔渣与电极之间接触面积的大小。不同电极直径下熔渣电场分布如图7所示。可以看出,随着电极直径的增加,电场线密度增大,电场强度增加,当电极直径达到一定值后,电场强度变化不明显。当电极面积小于熔渣截面积时,位于电极附近的电场线集聚,此处的电场强度较大,而位于圆柱体模型中间的电场线明显较稀疏,该处的电场强度较小。

图7 不同电极直径下熔渣的电场线分布(电压6 V,H/H0=0,熔渣介电常数6)Fig.7 Distribution of electric field lines of slag with different diameters of electrode(voltage of 6 V,H/H0=0 and slag permittivity of 6)
由式(2)计算得到系统电场能量随电极直径的变化如图8所示。可以看出,当D/D0达到0.8后,电场能量的增长趋势明显减缓。这是因为当电极与熔渣的接触面积增大到一定程度后,影响系统电场强度的主导因素不再是电极直径,而是外加电压等其他因素。在其他电场参数不变的条件下,增加电极尺寸可以在一定程度上提高系统电场能量,也是提高电场强度的有效手段。

图8 电场能量随电极直径的变化(电压6 V,H/H0=0,熔渣介电常数6)Fig.8 Electric field energy versus electrode diameter(voltage of 6 V,H/H0=0,slag permittivity of 6)
2.4 电极插入深度的影响
在实际操作过程中电极插入深度可以由外力控制,改变电极插入深度会对熔渣内电场分布产生一定影响。不同电极插入深度下熔渣电场线分布如图9所示。可以看出,随着电极插入深度的增加,系统的电场强度升高。这是因为随着电极插入深度的增加,两电极间距离缩短,而电流从阳极流入阴极,因此在外加电压不变的条件下,电场强度随两电极间距离的缩短而增加;当电极插入深度大于零时,熔渣上部出现无矢量箭头的电场,这是与电极相同的电势体,是电极两侧都存在电荷,并且电荷密度大小相等,电场线方向相反,正负电极的外部电场叠加后为零所导致的。

图9 不同电极插入深度下熔渣的电场线分布(电压6 V,D/D0=1,熔渣介电常数6)Fig.9 Distribution of electric field lines in slag at different electrode insertion depths(voltage of 6 V,D/D0=1 and slag permittivity of 6)
由式(2)计算得到系统电场能量随电极插入深度的变化如图10所示。可以看出,系统电场能量随电极插入深度的增加而增大,当H/H0达到0.6后,系统电场能量急速增大。这是因为随着两电极间距离的缩短,电极间电流变得更为密集,电流在熔渣底部产生大量的热,而电流热效应产生的功会使整个系统内的电场能量增大[13]。

图10 系统电场能量随电极插入深度的变化(电压6 V,D/D0=1,熔渣介电常数6)Fig.10 System field energy versus electrode insertion depth(voltage of 6 V,D/D0=1,slag permittivity of 6)
2.5 熔渣介电常数的影响
熔渣介电常数与其组分密切相关,也会对熔渣电场分布产生一定影响。不同熔渣介电常数下熔渣的电场线分布如图11所示。由于可将试验模型看作一个简易的电容器,因此电场强度的计算公式为:
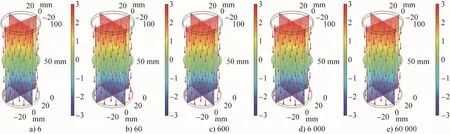
图11 不同熔渣介电常数下熔渣的电场线分布(电压6 V,D/D0=1,H/H0=0)Fig.11 Distributions of electric field lines in slag under different slag permittivities(voltage of 6 V,D/D0=1 and H/H0=0)

式中Q为电容器所带电荷。
在其他参数不变的条件下,系统电场强度随熔渣介电常数的增大而减小。在外加电场条件下熔渣中会产生感应电荷,感应电荷生成的感应电场与外加电场的电场强度方向相反,所以增大熔渣介电常数会减弱外加电场的电场强度。
由式(3)计算得到系统电场能量随熔渣介电常数的变化如图12所示。可以看出,系统电场能量随熔渣介电常数的增加而线性增加,增大熔渣介电常数是提高系统电场能量的有效途径之一。

图12 电场能量随熔渣介电常数的变化(电压6 V,D/D0=1,H/H0=0)Fig.12 Electric energy versus slag permittivity(voltage of 6 V,D/D0=1 and H/H0=0)
3 结论
(1)采用COMSOL软件模拟得到外加直流电场条件下熔渣电场线均由正极射向负极,两极间的电压差由大变小,电场强度方向与电场线方向一致。当电极面积小于熔渣截面积时,电极附近电场线集聚,远离电极处的电场线比较稀疏。两电极间的电场分布较规则,各部分电势比较稳定。模拟结果符合电场线的分布规律,表明用该模型模拟外加直流电场条件下熔渣的电场线分布是可行的。
(2)外加电压、电极直径和插入深度以及熔渣介电常数都对熔渣电场分布和系统电场能量产生一定影响。随着外加电压、电极直径和电极插入深度的增加,系统电场能量和电场强度均逐渐增大,而随着熔渣介电常数的增大,系统电场强度降低,电场能量增加。
