一种基于雷达信号参数的未知目标干扰策略分析技术研究
2021-09-25王秀锦姚金垠
王秀锦,姚金垠
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
针对未知目标的干扰是电子对抗系统长期以来不得不面对的情况。近年来,弹道导弹技术的发展对于各种型号的舰艇反导压力越来越大。针对多目标同时来袭,在干扰资源有限的情况下,如何最大限度地利用有限的干扰资源对我舰形成最有效的保护成为了亟需解决的问题。
威胁度是电子对抗系统侦收目标过程中的一个非常重要的指标。其目的是获取敌方目标相对我舰的威胁等级,在电子对抗系统干扰资源有限的情况下,帮助我方迅速准确地判断优先选择的目标。目前,威胁目标的威胁度判断方法有很多种,包括模糊推理法[1]、频点判断法[2]、神经网络算法[3]等,这些方法能够在一定程度上解决电子对抗系统威胁度判定问题,但是其适应能力有限,在战场模糊环境下很难精确得到多批目标相对我舰的相对威胁度,特别在干扰资源有限的情况下很难利用有限的资源对我舰形成最有效的保护。
本文引入模糊神经网络算法,对该算法进行分层定义,采用三层次模糊神经网络算法,对电子对抗系统的高威胁目标进行快速分析,推理出多批威胁目标相对我舰的相对威胁度等级,从而帮助电子对抗系统进行干扰对抗决策,充分利用电子对抗系统的干扰能力,对一批或者多批威胁等级最高的目标进行干扰,最大限度地保障我舰安全。
1 基于模糊理论的目标威胁隶属度函数的确定
模糊系统的基本原理是多个模糊化的输入向量经过给定规则的推理机制,变成一个或者多个去模糊化的输出向量,如图1所示。

图1 模糊系统基本原理
推理过程大致如下:
(1) 比较输入变量和隶属函数,从而获得每个语言标示的隶属值——模糊化。
(2) 对初始部分的隶属函数做并运算,得到每个规则的激活权。
(3) 依赖于激活权产生每一个规则的有效结果。
(4) 叠加所有有效的结果产生一个明确的输出——去模糊化。
1.1 威胁隶属度[4]定义
在模糊系统中,被讨论对象的全集称为论域,用U表示,在论域U上选定1个模糊子集A。Φ(u)表示u隶属于A的程度,简称隶属度。
在目标的威胁度模糊系统中,选取目标距离r、目标速度v、目标航向夹角θ作为威胁等级的输入向量即特征向量。选取目标相对我方的威胁度作为威胁等级加权的决定因素,建立基于目标的威胁等级。
1.2 威胁隶属度函数分析
利用模糊理论对威胁隶属函数进行描述,并建立规则如下:当某个特征向量对于我方的威胁度越大时,其威胁等级也就越大(当特征向量值为最大时,此时威胁函数评判值定为1);当某个特征向量对于我方的威胁度越小时,其威胁等级也就越小(当特征向量值为最小值时,此时威胁函数评判值定为0);当特征向量处于最大值和最小值之间时,威胁函数评判值介于0~1之间。
建立威胁等级与目标距离之间的关系。当威胁目标距离小于20 km时,威胁目标对我方威胁最高,设威胁评判值为1;当威胁目标距离大于500 km时,认为威胁目标对我方无威胁,威胁评判值为0。设在实战环境下目标距离与威胁等级之间服从降半正太分布:
(1)
式中:r1=20 km;r2=500 km。
建立威胁等级与目标速度之间的关系。当威胁目标速度越高时,对于我方的反应时间也就变得越少。因此,可以认为目标的威胁等级也就越高。可以将速度与威胁等级设为线性关系,其评判函数为:
(2)
式中:v0=200 m/s。
考虑到目前战斗机的速度基本上都在200 m/s以上,导弹的速度一般在340 m/s以上,因此当威胁目标的速度小于200 m/s时认为无威胁,设威胁评判值为0;当威胁目标的速度大于340 m/s时认为该目标高威胁,设威胁评判值为1。
建立威胁等级与目标航向夹角之间的关系。当威胁目标航向与我方航向夹角越接近0°时,其对我方的威胁度越高。同理可以建立航向夹角的隶属度函数为:
(3)
式中:θ0=π/2。
综上可得威胁隶属度函数集合为:
Φ=(Φ(r),Φ(v),Φ(θ))
(4)
2 基于三层次模糊神经网络的威胁
2.1 特征向量权重判定
不同的特征向量对于判断威胁目标的威胁等级的权重是不同的,因此必须建立准确的判断准则对不同的特征向量进行加权分配。本文采用AHP层次分析法[5]对不同特征向量建立不同的权重值。
首先建立七层次的判断规则,规则如表1所示。

表1 特征向量权重判断规则
然后根据建立的权重判断规则获取不同影响因素之间的威胁层次,得到威胁层次向量:
L=(t1,t2,…,tn)
(5)
将威胁层次向量归一化,最终得到的向量即是威胁因素权重向量:
L′=(t′1,t′2,…,t′n)
(6)
2.2 三层次模糊神经网络建立
本文按照3个层次建立目标威胁度等级网络模型,如图2所示。
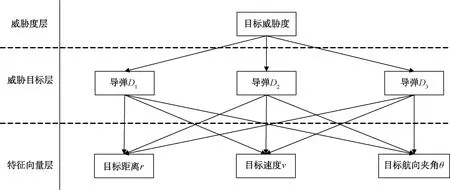
图2 三层次模糊神经网络结构图
特征向量层表示表征目标威胁度影响力最大的参数因子集合,它能够直接或者间接反映目标的威胁度。威胁目标层表示敌方目标集合,它可以是导弹,也可以是敌方雷达或者飞机等威胁类型。威胁度层表示最终想要得到的目标参数,即目标威胁度。
2.3 目标威胁度向量表
根据1.2章节介绍的目标威胁度隶属函数,求得目标威胁度向量函数为:
Φ=(Φ(r),Φ(v),Φ(θ))
(7)
然后对函数进行归一化处理,保证向量的值都在统一的标尺内,得到归一化后的目标威胁度向量表为:
Φ′=(Φ′(r),Φ′(v),Φ′(θ))
(8)
最后第i个目标的威胁度等级为:
Wi=Φ′i·(L′)T
(9)
3 实例验证
为验证本文方法的有效性,现假定有3个导弹目标D1,D2,D3来袭,雷达探测的导航参数如表2所示。
针对这3批导弹目标,首先建立威胁层次向量:
L=(t1,t2,t3)=(3,4,5)
归一化处理得到威胁因素向量:
L′=(t′1,t′2,t′3)=(0.424 3,0.565 7,0.707 1)

表2 导弹目标导航参数表
然后分别计算目标威胁度向量表,导弹D1的威胁度向量为:
Φ1=(0.890 2,0.714 3,0.959 2)
归一化处理:
Φ′=(0.597 1,0.479 1,0.643 4)
导弹D1的威胁度等级为:
W1=Φ′1·(L′)T=0.979 3
同理可得导弹D2的威胁度等级为:
W2=Φ′2·(L′)T=0.903 1
导弹D3的威胁度等级为:
W3=Φ′3·(L′)T=0.805 8
根据计算结果得出导弹D1威胁度最高,导弹D2居中,导弹D3的威胁度最低。当这3种导弹同时来袭时,在干扰资源只能够干扰1枚导弹时,可以优先对导弹D1进行干扰,当干扰资源能够干扰2枚导弹时,可以优先对导弹D1和D2进行干扰。
4 结束语
针对空中多批未知目标的干扰策略分析问题,本文提出了基于雷达信号参数的威胁度分析技术。通过理论分析和实例验证表明,结合模糊理论的威胁度等级分析技术能够有效地对空中多批目标的威胁度相对等级进行分析判断,最终得出针对多批目标的干扰策略,具有很高的工程运用价值。
