LGA 焊点可靠性分析及热疲劳寿命预测

金玲玥,孙海燕,周 婷,赵继聪

(南通大学 信息科学技术学院,江苏 南通 226019)

物联网将人们带入万物皆可互联的时代,而窄带物联网(Narrow Band Internet of Things,NB-IoT)作为以物联网为基础的一种新式通信方法,以其耗能低、覆盖面广、数据连接性能佳等优势被广泛应用于各个领域[1-3]。随着科技不断发展,窄带物联网应用规模越来越大,也使人们对承载其功能的封装结构提出了更高的要求。将先进系统级封装(System in Package,SiP)技术应用于窄带物联网,可使得更多功能芯片能集成在一个封装体内,实现小型化、多功能化的目标[4]。

栅格阵列封装(Land Grid Array,LGA)的底部没有焊球,通过在印制电路板(Printed Circuit Board,PCB)上的焊盘刷焊膏进行回流焊以完成连接[5]。该连接方式大幅缩短了互连距离,有效地提高了电气性能,越来越多的便携式电子产品选择LGA 封装形式。由于材料间热膨胀系数的不匹配,在温度或者功率循环过程中,热应力和塑性应变会累积在焊点中,严重情况下将导致焊点失效[6]。为使产品具有更高的可靠性,研究焊点在外部载荷作用下结构和材料的动态响应具有较高的实际价值。

国内外学者也针对LGA 焊点进行了一系列的研究。Yang 等[7]对板级LGA 无铅焊点进行热可靠分析,利用X-ray 设备检测,发现有机衬底上板级LGA 焊点在热循环载荷下具有更高的可靠性;赵志斌等[8]使用Surface Evolver 软件预测LGA 焊点形态,得出PCB 焊盘的大小与开孔固定模板的厚度对焊点形态的影响较大;徐婷婷[9]将二次焊接工艺应用到LGA 器件,从有限元分析和试验角度验证了LGA 焊点二次焊接后,有效地降低焊点的空洞率,同时提高了焊点的热可靠性,达到航天电子产品的生产需求。本文基于一款LGA 封装外形的NB-IoT 系统级封装芯片,为提高其焊点可靠性,设计了一种焊料包裹焊盘的倒凹槽焊点形态。在-40～125 ℃的温度循环条件下,根据修正的Coffin-Manson 方程进行热疲劳寿命预测[10]。最后,基于田口试验法建立L27(39)正交表,得到焊点可靠性最优的组合参数,为工程实践提供了参考。

1 模型的建立

1.1 有限元建模

图1 为NB-IoT 系统级封装-PCB 实物图,中间部位为NB-IoT 系统级封装芯片,采用LGA 封装外形与PCB 相连。图2(a)为根据图1 建立的有限元仿真模型,三维模型中包括PCB、铜焊盘、焊点、芯片、塑封料等,详细结构尺寸见表1。图2(b)和(c)分别为常规焊点和倒凹槽焊点模型,常规焊点是将焊料直接叠加在PCB 侧焊盘上面,倒凹槽焊点是用焊料将PCB侧焊盘包裹起来,增大焊点与焊盘的接触面积,提高焊点的热可靠性。

图1 NB-IoT 系统级封装-PCB 实物图Fig.1 Specimen of NB-IoT SiP-PCB

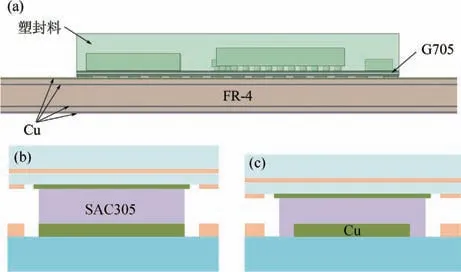
图2 (a)封装-PCB 仿真模型;(b)常规焊点;(c)倒凹槽焊点Fig.2 (a) Simulation model of package-PCB;(b) Traditional solder joint;(c) Inverted groove solder joint

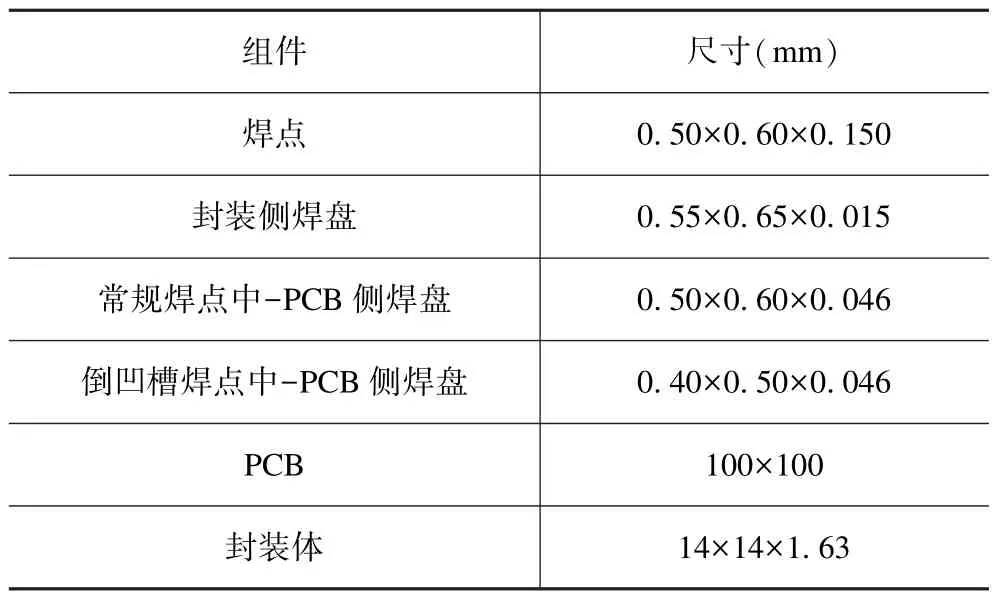
表1 封装-PCB 的结构参数Tab.1 Structure parameters of package-PCB

1.2 材料参数

表2 是各个组件的材料属性[11],包括锡银铜焊料(SAC305)、FR-4、G705、铜、塑封料。

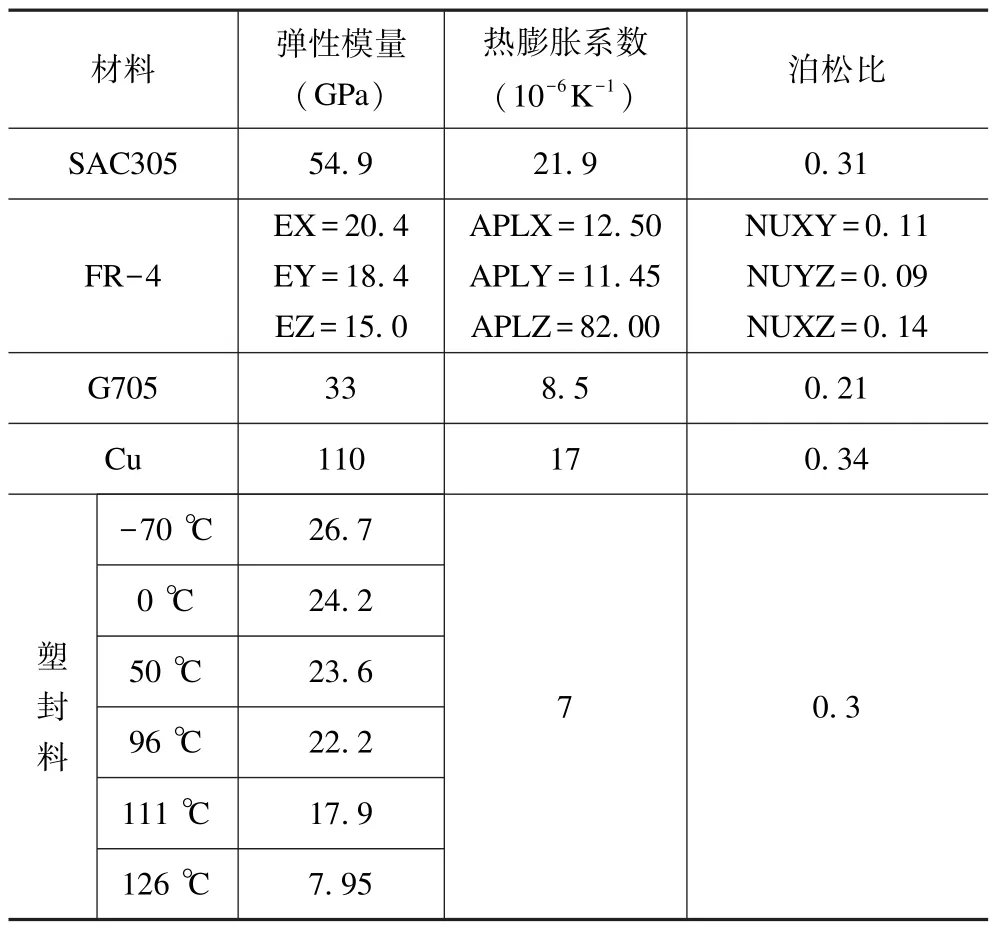
表2 封装-PCB 组件的材料参数[11]Tab.2 Material parameters of package-PCB[11]

SAC 系列合金材料的粘塑性在载荷(如温度载荷)作用下表现明显,Anand 模型在模拟试验中可以很好地描述粘塑性材料与应变速率、温度有关的变形行为。Anand 本构模型的流动方程表达式如下:

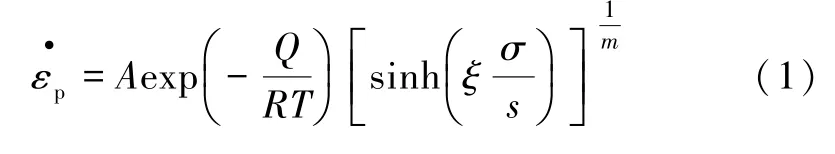
公式(1)与内部变量的演化方程成为Anand 基本方程,其中内部变量可描述为:

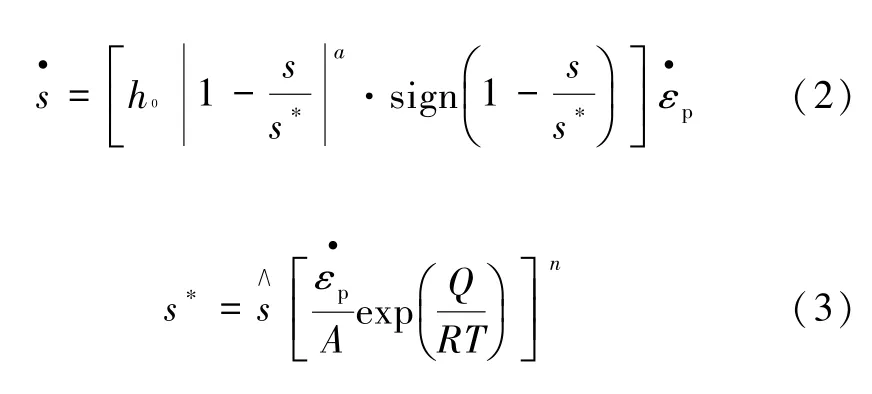
式中:h0为硬化/软化常数;a为硬化/软化的应变敏感值;s∗为给定温度和应变速率下形变阻抗的饱和值;为形变阻抗饱和系数;n为应力-应变率敏感度。

焊点材料为SAC305,使用Anand 模型描述焊料的粘塑性行为[12],如表3 所示。

表3 SAC305 的Anand 材料参数[12]Tab.3 Anand material parameters of SAC305[12]

1.3 加载条件

根据JESD22-A104C Temperature Cycling 中的条件G,设定温度循环范围为-40～125 ℃,加载曲线如图3 所示,升、降温速率均为16.5 ℃/min,高、低温保持时间均为15 min。由于焊点的等效塑性应变在第4 个周期较为稳定,因此有限元分析中选取4 个温度循环周期[13]。

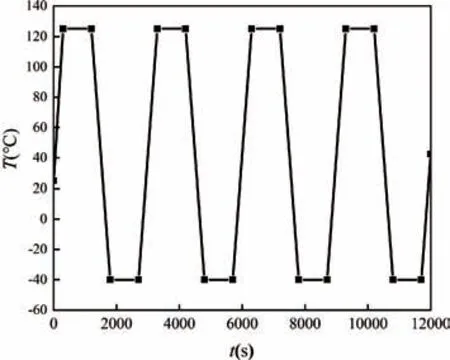
图3 温度循环曲线Fig.3 Temperature cycling curve

1.4 疲劳寿命预测模型

本文运用修正的Coffin-Manson 模型评估LGA 焊点的热疲劳寿命。通过引入单个循环累积的等效塑性应变[14],建立等效塑性应变与疲劳寿命的关系,得到焊点的疲劳寿命,其表达式为:

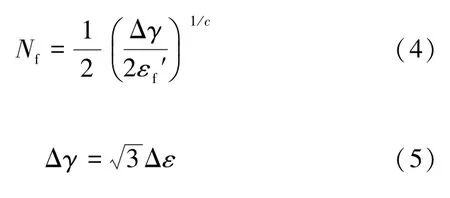
式中:Nf为焊点的疲劳寿命;Δγ为等效剪切应变范围;Δε为等效塑性应变范围;εf′为疲劳韧性系数,值为0.325;c为疲劳扩展系数。

2 焊点结构对疲劳寿命的影响

2.1 常规焊点的热疲劳寿命分析

对常规焊点模型进行有限元分析,图4 为常规焊点的等效塑性应变分布图和等效应力分布图,最大等效塑性应变为3.7108×10-2,最大等效应力为49.71 MPa。从图4 中发现等效塑性应变和等效应力最大的位置都位于边角处焊点与PCB 侧焊盘的连接处。本文将边角处焊点看作关键焊点,即图中Max 标志处。

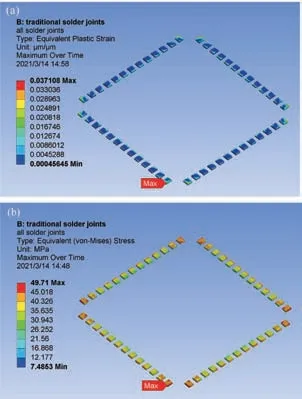
图4 (a)常规焊点的等效塑性应变分布云图;(b)常规焊点等效应力分布云图Fig.4 (a) The equivalent plastic strain distribution diagram of the traditional solder joints;(b) The equivalent stress distribution diagram of the traditional solder joints

图5 为常规焊点模型仿真得到的等效塑性应变与时间的关系图。从图中分析,焊点的等效塑性应变随温度载荷呈现周期性变化。图中第4 个周期累积的等效塑性应变为0.6732×10-2,根据公式(4)和(5)可得,常规焊点的热疲劳寿命为578 个周期。

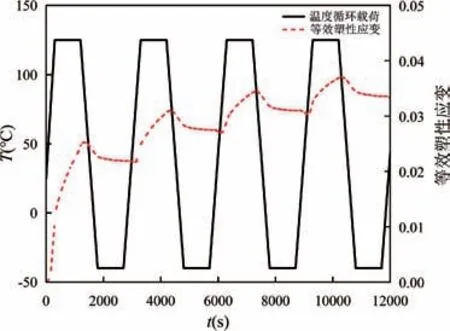
图5 常规焊点等效塑性应变与时间的关系Fig.5 The relationship between equivalent plastic strain and time of the traditional solder joints

进一步将常规焊点模型对应的样品A 进行温度循环试验,在500 个周期后取出,对关键焊点进行断面,断面图如图6(a)所示。为了对比验证,图6(b)所示为关键焊点的等效塑性应变分布云图,最大等效塑性应变为3.7108×10-2,焊点的危险位置位于左下角与PCB 侧焊盘接触处,与试验结果裂纹趋势一致。

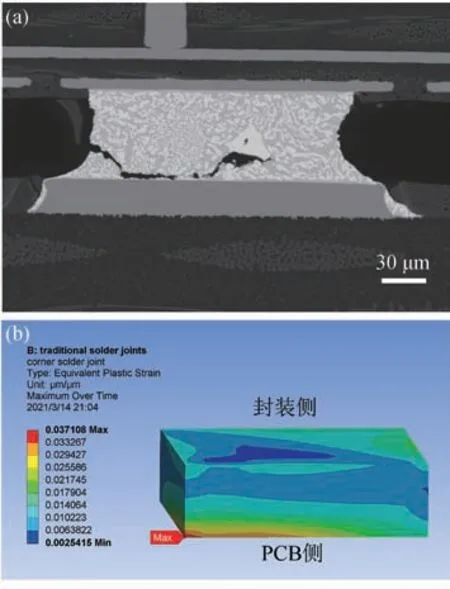
图6 (a)常规焊点结构中关键焊点的断面图(裂纹位置);(b)常规焊点结构中关键焊点的塑性应变分布云图Fig.6 (a) Cross section of the key traditional solder joint (Crack location);(b) The equivalent plastic strain distribution diagram of the key traditional solder joint

2.2 倒凹槽焊点的热疲劳寿命分析

同理,图7 为倒凹槽焊点模型仿真得到的等效塑性应变与时间的关系图,倒凹槽焊点的等效塑性应变趋势与常规焊点类似,焊点在第4 个周期累积的等效塑性应变为0.4439×10-2,计算可得热疲劳寿命为1201 个周期。

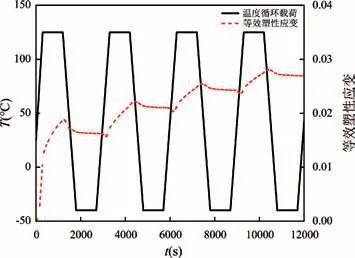
图7 倒凹槽焊点的等效塑性应变与时间的关系Fig.7 The relationship between equivalent plastic strain and time of the inverted groove solder joints

将倒凹槽焊点模型对应的样品B 在1000 个周期后取出,同样对关键焊点进行断面,断面图如图8(a)所示。对比图8(b)倒凹槽焊点结构中关键焊点等效塑性应变分布云图可知,发现此焊点的断面图未有裂纹,对应关键焊点的最大等效塑性应变为2.8109×10-2,比常规焊点降低了24%。证明倒凹槽焊点的热可靠性优于常规焊点。

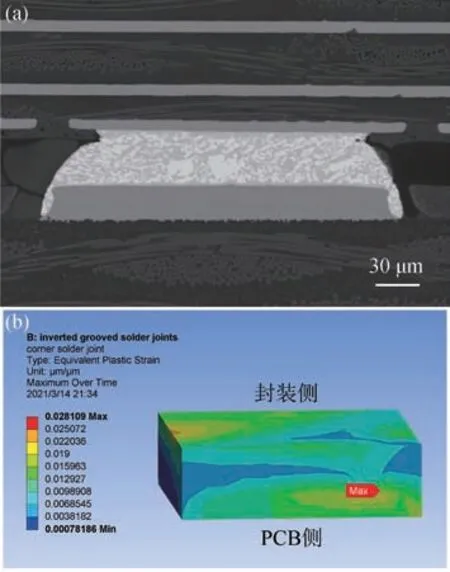
图8 (a)倒凹槽焊点结构中关键焊点的断面图;(b)倒凹槽焊点结构中关键焊点等效塑性应变分布云图Fig.8 (a) Cross section of the key inverted groove solder joint;(b) The equivalent plastic strain distribution diagram of the inverted groove solder joint

3 倒凹槽焊点的优化设计及分析

3.1 单一因素分析

为更深入地研究封装结构、温度载荷、材料属性等方面因素对LGA 焊点热疲劳寿命的影响,本文共选取13 个因素,如表4 所示,每个因素均选取3 个水平,其中水平2 代表初始倒凹槽焊点的设计参数。

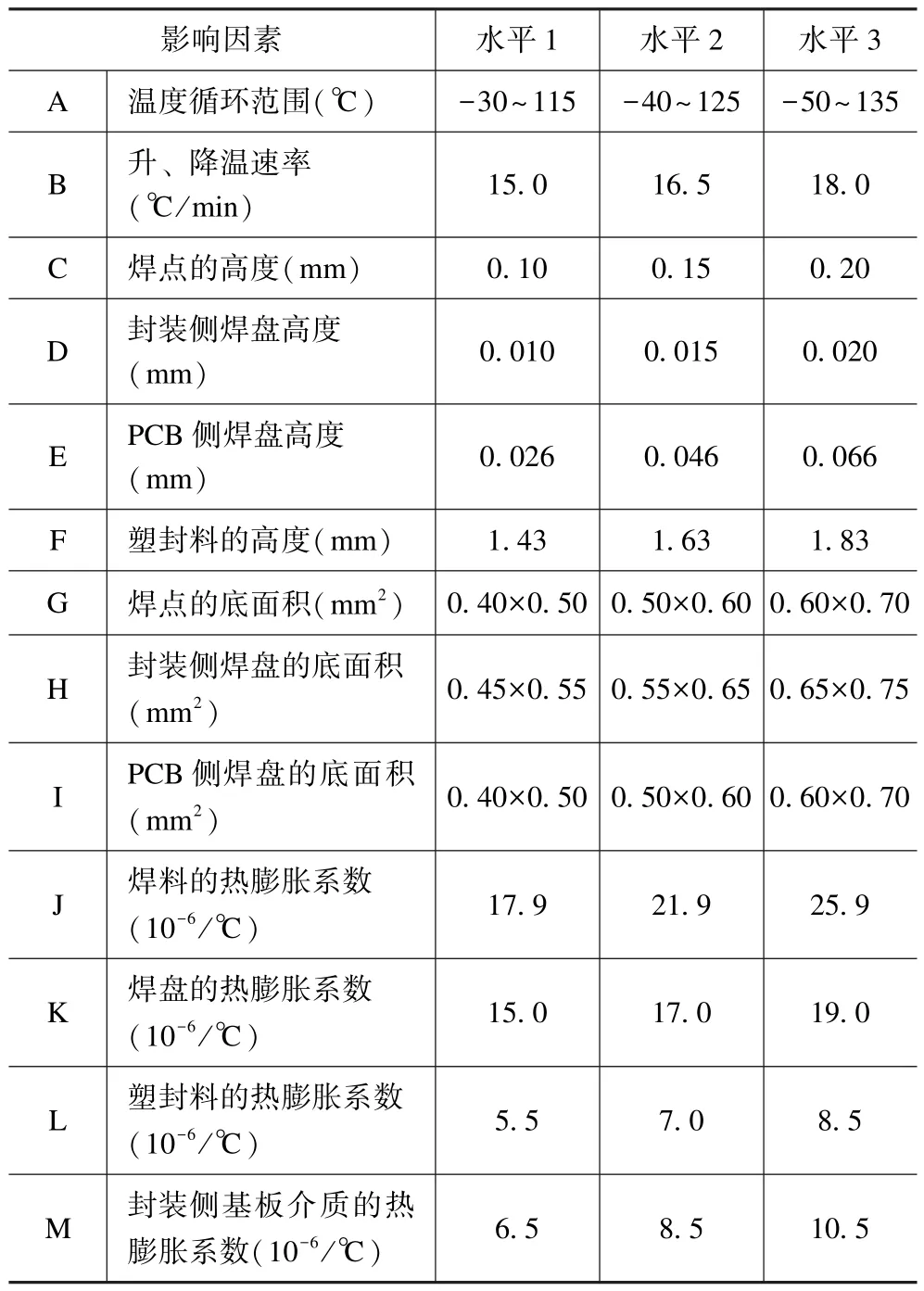
表4 因素水平表Tab.4 The level of factors

采用单因素分析法,即一次只改变一个因素,研究其对焊点热疲劳寿命的影响。当此因素对焊点热疲劳寿命的影响程度达20%时,则定义该因素为显著因素[15]。

由单因素分析法可得,在13 个因素中有9 个显著因素,分别为:温度循环范围(A)、焊点的高度(C)、PCB 侧焊盘的高度(E)、焊点的底面积(G)、PCB 侧焊盘的底面积(I)、焊料的热膨胀系数(J)、焊盘的热膨胀系数(K)、塑封料的热膨胀系数(L)、封装侧基板介质的热膨胀系数(M)。

3.2 田口试验法

单因素法分析结果揭示显著因素依旧较多。本文进一步结合田口试验法[16-18],构建正交表L27(39)对9个显著因子进行试验,共27 组试验。本文试验的目标函数是LGA 焊点的热疲劳寿命[19],即希望响应最大化,因此采用望大特性信噪比公式:

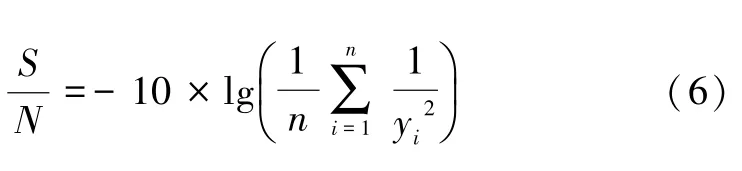
式中:n为相同参数条件下的试验次数,试验采用的是有限元分析法,因此n取1;yi为试验值,即计算所得的热疲劳寿命。试验结果如表5 所示,由表5 可以看出,第5组试验的信噪比最大,此组的热疲劳寿命最高,第15 组试验的信噪比最小,此组的热疲劳寿命最低。

根据表5,将27 组试验结果通过极差法计算得各个因素水平的平均信噪比和各因素对焊点热疲劳寿命的影响等级,分别如图9 和表6 所示。从图9 和表6中可得,影响焊点热疲劳寿命各因子的排列顺序为L>A>E >C >K >M >G >J >I,相应的参数组合是A1C1E2G3I2J2K2L3M3。

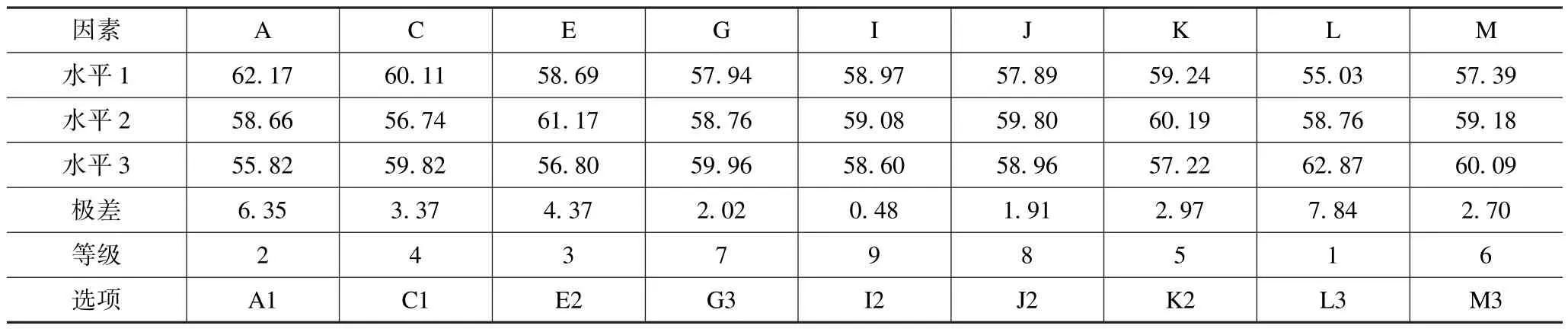
表6 信噪比响应平均效应Tab.6 Average effect respond for signal-to-noise ratio

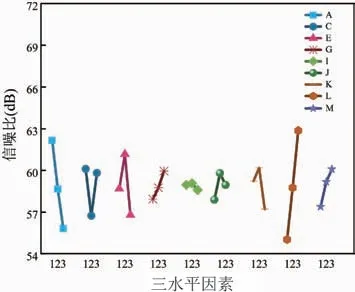
图9 信噪比响应平均效应Fig.9 Average effect respond for signal-to-noise ratio

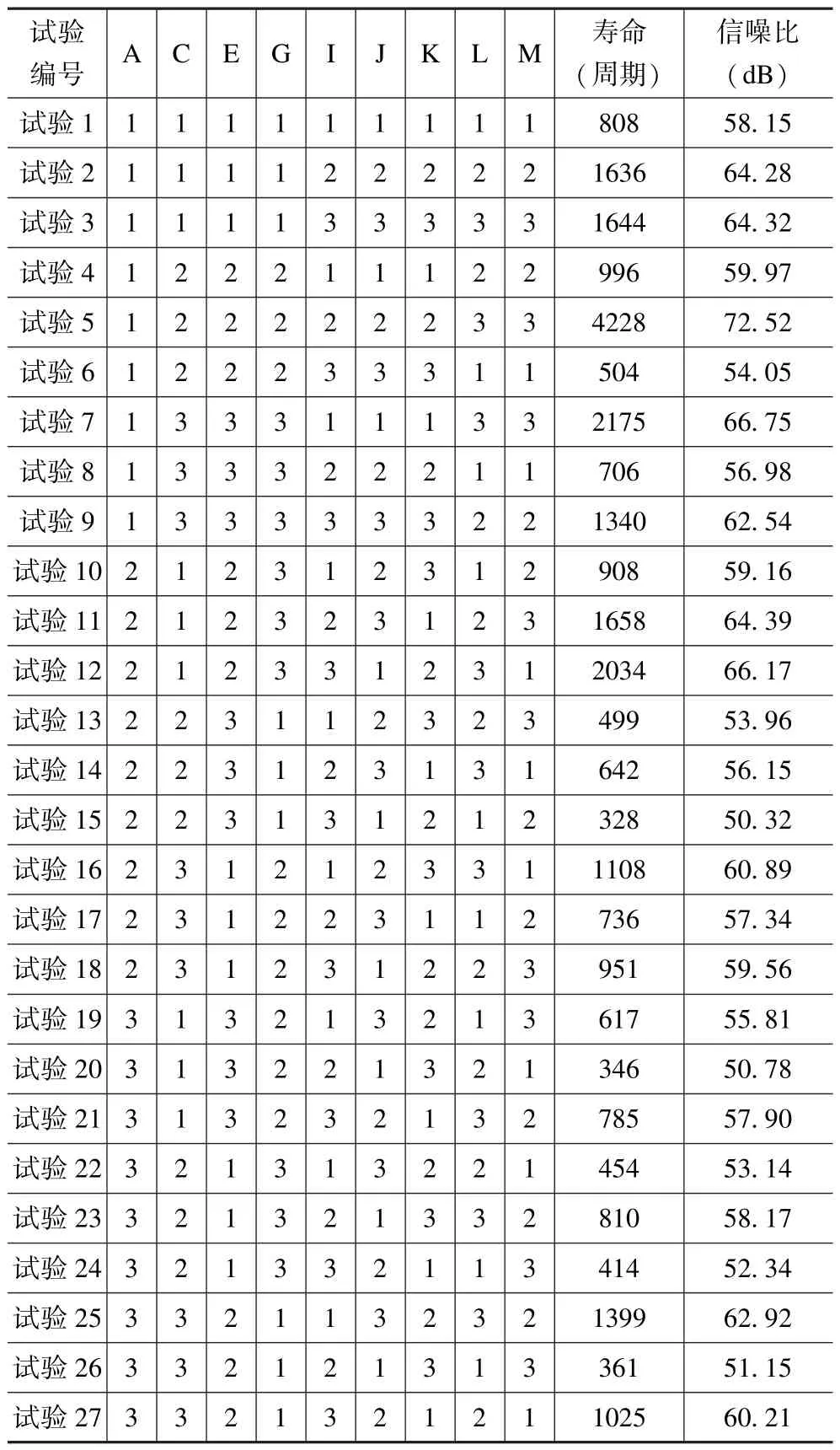
表5 焊点疲劳寿命与信噪比试验结果Tab.5 The experimental results of fatigue life and signal-to-noise ratios

基于上述试验所得的最佳参数组合,构建最终的倒凹槽优化模型。经有限元分析得到优化后倒凹槽焊点的等效塑性应变与时间关系图,如图10 所示,从图中可以得到优化后倒凹槽焊点在第4 个周期累积的等效塑性应变值为0.2147×10-2,相应的热疲劳寿命为4297 个周期。

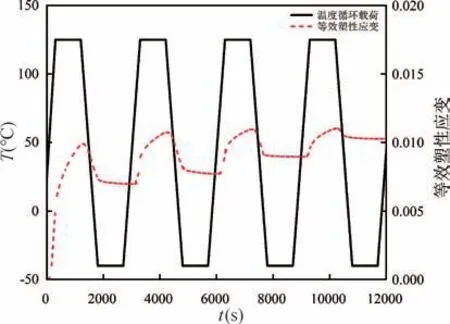
图10 优化后倒凹槽焊点的等效塑性应变与时间的关系Fig.10 The relationship between equivalent strain and time of the optimal inverted grooved solder joints

图11 进一步给出了最佳参数组合下封装的等效塑性应变分布图和等效应力分布图,其中最大塑性应变为1.1015×10-2,最大等效应力为44.465 MPa,相比传统焊点分别降低了70.31%和10.55%,倒凹槽优化模型有效地提高了LGA 封装的热可靠性。

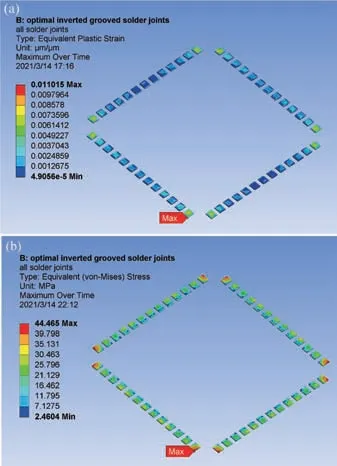
图11 (a)优化后倒凹槽优化焊点的等效塑性应变分布云图;(b)优化后倒凹槽优化焊点的等效应力分布云图Fig.11 (a) The equivalent plastic strain distribution diagram of the optimal inverted groove solder joints;(b) The equivalent stress distribution diagram of the optimal inverted groove solder joints

4 结论

本文主要研究了LGA 焊点的热疲劳可靠性,得出如下结论:

(1)温度循环载荷下,焊点最大应力处位于边角处焊点与PCB 侧焊盘接触面,是最有可能失效的位置。

(2)设计了一种焊料包裹焊盘的倒凹槽焊点形态,利用修正的Coffin-Manson 模型进行热疲劳寿命预测。仿真和试验证明倒凹槽焊点的热疲劳寿命明显高于常规焊点。

(3)对倒凹槽焊点进行优化,得到最优参数组合下LGA 焊点的热疲劳寿命为4297 个周期,是常规焊点的7.43 倍。