异常数据对继电保护影响的仿真实验分析

2021-09-24郝俊伟

电气传动自动化 2021年2期

郝俊伟

（山西杏花村汾酒集团有限责任公司，山西吕梁 032205）

随着信息技术、通信技术和计算机技术的快速发展，智能变电站也得到了快速发展。智能变电站中的信号采集设施主要由电子仪表变压器和合并单元组成。但生产技术的不成熟给电子仪表变压器的使用带来了一些问题，其中异常数据是最严重的问题之一。

因为数据异常而导致的事故报告很多。如何降低异常数据的影响是一个非常重要的研究方向，文献［1－2］中都有讨论。文献［3］对如何检测异常数据给出了一些方法，但对异常数据的影响缺乏研究。本文在深入研究了异常数据的特性和智能变电站的特点后，定义了五个参数来描述异常数据的影响，并且研究了异常数据对傅里叶算法和继电保护的影响。

1 异常数据的特征和影响

1.1 异常数据的特征

异常数据是并不属于特定族群的数据点，是与其它数值相距甚远的异常数据。异常数据的特征可以用均匀度、相位、误差值、替代度和持续时间等五个参数来描述（如图1）。

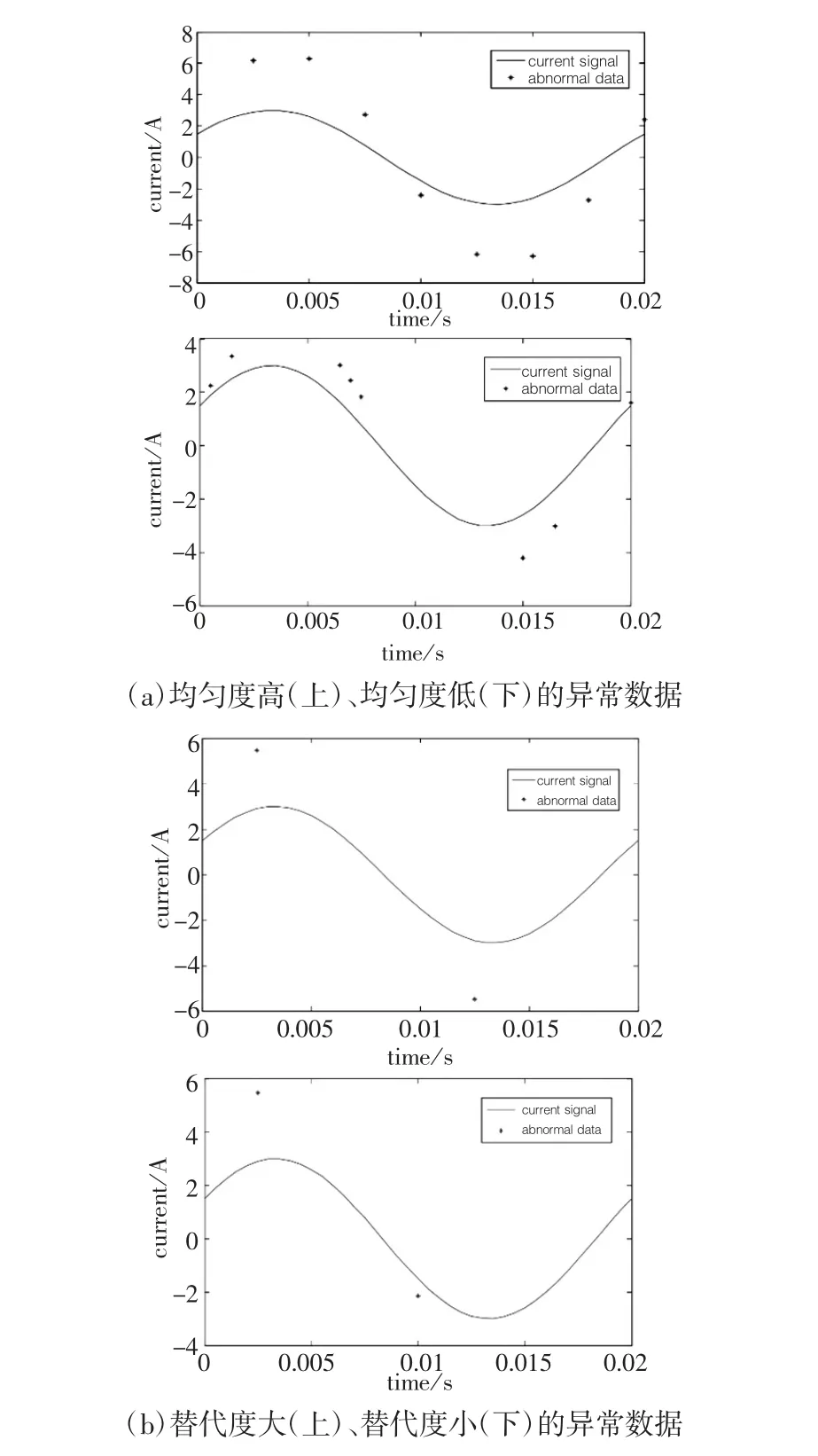
图1 异常数据特征图

均匀度描述的是相邻两个异常数据之间的差距。均匀度越高，异常数据对继电保护系统的影响越大。

相位描述异常数据的相位和位置。如果异常数据发生在信号的峰值，则影响最大；如果发生在零交叉点，则影响最小；在其他位置上，则影响处于中间位置。误差值描述的是异常值与正常值之间的差异。误差值越大，影响越大。替代度是指一对相邻的异常数据值的不同符号的角度差，替代度越大影响越大，替代度越小影响越小。持续时间描述异常数据持续的时间，持续时间越长影响越大。

1.2 异常数据对傅里叶算法的影响

傅里叶算法在继电保护中得到了广泛的应用，因为它具有速度快、实现简单、可靠性高等优点，而且它可以分离不同的频率成分。本文分析了异常数据对傅里叶算法的影响。假设对于正弦信号，每个周期有N个采样点，正弦信号的幅值为A，异常数据到峰值的距离为M。xN［i］是正弦信号的第ith个采样值，异常数据出现在第n个点，其值等于x′N［n］。原始基波振幅的表达式为：

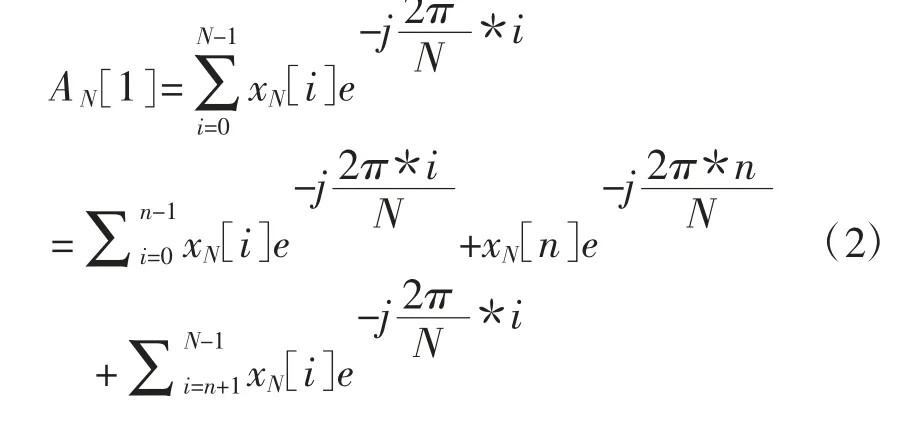
带有异常数据的基波振幅的表达式为：

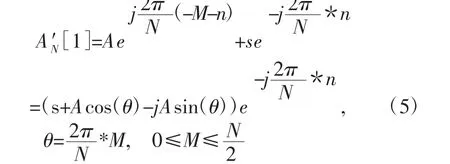
因此，异常数据信号幅度的误差为

从式（6）可以看出，当s变大而M变小时，信号幅度的误差变大。由此可以合理地得出结论：异常数据的误差值越大，异常点越靠近峰值，则异常数据对通过傅里叶算法计算的结果的影响就越大。

2 异常数据对继电保护的影响

2.1 异常数据对距离保护的影响

为了测试异常数据对距离保护的影响，建立了如图2所示的仿真模型。

图2 异常数据对距离保护影响的仿真模型图

在仿真模型中，L1的长度为20km，L2的长度为15km。L1上的电流在40A至50A之间变化，L3上的电流在35A至40A之间变化。L1上的最小保护分支系数等于1.7。根据距离保护理论，通过等式（7）和等式（8）来计算保护的设定值。

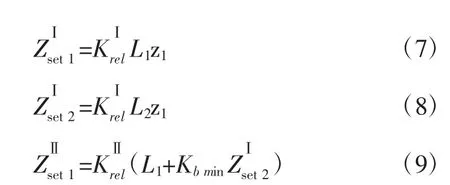
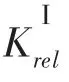
2.2 异常数据对过电流保护的影响

为了测试异常数据对过电流保护的影响，本文也建立了仿真模型，如图3所示。

图3 异常数据对过电流保护影响的仿真模型图

1号线的长度为20k m。S1的相间均方根电压为35k V。S2的相间均方根电压为10k V。负载1的额定有功功率为20k W，其感性功率因数为0.8。负载1的有功功率因数为0.8。负载2的额定有功功率为15k W，其感性功率因数为0.6。Ⅰ和Ⅱ是系统的两个母线。保护A的安装位置非常靠近Ⅰ，而保护B的安装位置非常靠近Ⅱ。根据过电流保护的原理，通过等式（10）和等式（11）计算瞬时过电流保护的设定值并研究瞬时过电流保护的延时特性。