基于VMD样本熵和CS-ELM的滚动轴承故障诊断

王椿晶 王海瑞 关晓艳 常梦容

（昆明理工大学信息工程与自动化学院）

滚动轴承在重型旋转机械中应用广泛，若其运行状态出现问题，会导致整个机械设备停运甚至发生安全事故，进而造成直接经济损失。 因此，对滚动轴承的健康状态进行实时监测和故障诊断具有极其重要的意义［1］。

滚动轴承故障诊断的关键是如何从复杂的故障信号中提取出能表征故障特征的信息、提高故障识别的准确性。 然而，滚动轴承故障信号为非线性、非平稳信号，导致传统的特征提取方法存在模态混叠现象。 2014年，Dragomiretskiy K和Zosso D提出了变分模态分解 （Variational Mode Decomposition，VMD）方法，能有效克服模态混叠、边界效应及过分解等情况［2］。 钱林等将VMD和经验 模 态 分 解 （Empirical Mode Decomposition，EMD）方法进行比较，结果证明VMD提取故障特征的效果更好［3］。与近似熵相比，样本熵算法对时间序列的统计量具有更好的一致性，可较少地依赖于时间序列长度［4］，能够降低近似熵的误差，提高统计精度，因此比较适用于对复杂信号进行处理。超限学习机（Extreme Learning Machine，ELM）的网络结构是单层前馈型神经网络，它无需反复调整隐含层参数，相较于传统的分类方法，有着学习速度快、泛化性能好等优点［5］，但是ELM输入权值和隐含层神经元阈值的随机选择会影响算法的稳定性和分类准确率。

笔者以滚动轴承为研究对象，首先通过VMD处理不同工况下的滚动轴承信号， 得到多个IMF分量，然后求出各模态的样本熵并作为特征向量输入到布谷鸟搜索（Cuckoo Search，CS）算法优化的ELM分类器中，通过对参数进行优化，进一步提高分类准确率，实现不同工况下的轴承故障诊断识别。1 VMD样本熵

1.1 VMD算法

1.1.1 变分问题的构造

假设约束条件为：将滚动轴承故障信号f分解成k个本征模态uk， 使k个模态分量之和等于f，同时满足从变分模型中寻找的每个模态的估计带宽之和最小，即拥有有限带宽之和最小的中心频率。 则，约束变分模型的数学表达式为：

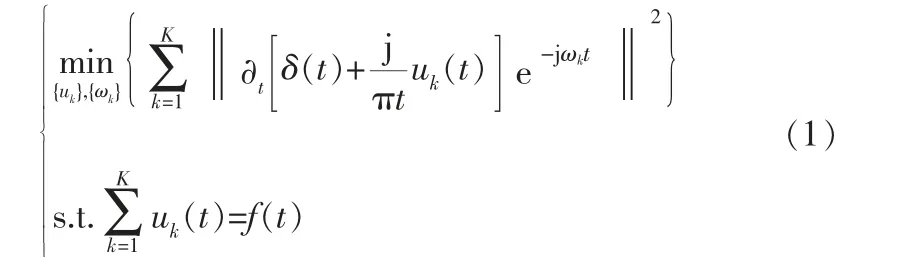
其中，uk为分解得到的IMF分量，{uk}={u1，…，uk}，ωk为IMF分量对应的中心频率，{ωk}={ω1，…，ωk}，K为IMF分量个数，δ为单位脉冲函数。

1.1.2 变分问题的求解

为了将式（1）由约束变分问题变为非约束问题进行求解， 需要引入拉格朗日乘法算子λ和二次惩罚因子α，得到函数表达式为：

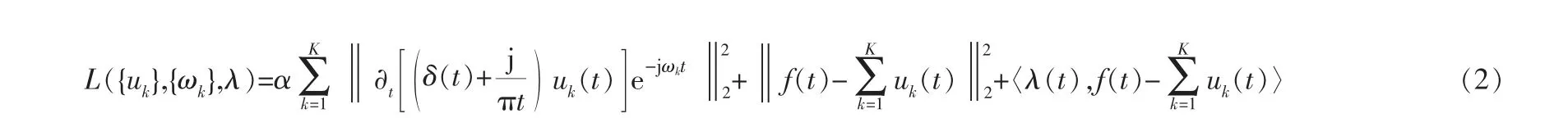
1.2 样本熵

样本熵是由Richman J S和Randall M J提出的一种新的时间序列复杂性的度量方法［6］，与近似熵方法类似，但是改进了近似熵存在的因对自身数据段的比较而产生计算偏差和一致性较差的缺陷［7］。

样本熵算法计算步骤如下：

a. 将时间序列{x（n）}=x（1），x（2），…，x（N）表示为m维向量Xm（1），Xm（2），…，Xm（N-m+1）。

2 CS-ELM

2.1 ELM

其中，wi=［wi1，wi2，…，win］T表示第i个隐含层单元的输入权重，βi=［βi1，βi2，…，βin］T表示第i个隐含层单元的输出权重，bi为隐含层神经元的阈值，g（·）为隐含层的激活函数，M为隐含层节点数，oi为网络输出值。

ELM的学习目的在于使得网络输出误差最小，因此需要满足：

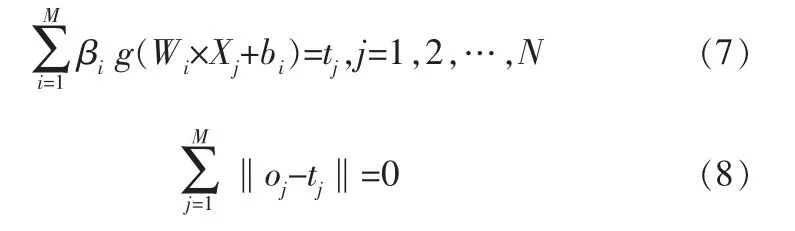
其中，Wi为输入权重，Xj为输出向量。

2.2 CS-ELM算法

ELM的输入权值和隐含层阈值是随机确定的，使得隐含层的一些节点处于无效状态，降低了算法的稳定性和分类准确率。 针对上述问题，采用CS算法［8］对ELM进行改进，自适应调节隐含层节点数，选取最优的一组输入权值和隐含层阈值，从而提高ELM的分类准确率［9］。

利用CS算法对ELM参数优化的具体流程如图1所示。在CS-ELM算法中，CS算法采用Levy飞行搜索机制，使用鸟巢的位置代表解，ELM的预测误差代表当前鸟巢的适应度值，通过不断迭代搜索，比较鸟巢对应的适应度值，输出最优鸟巢位置作为ELM的隐含层节点数， 并得到输入权值和隐含层阈值。

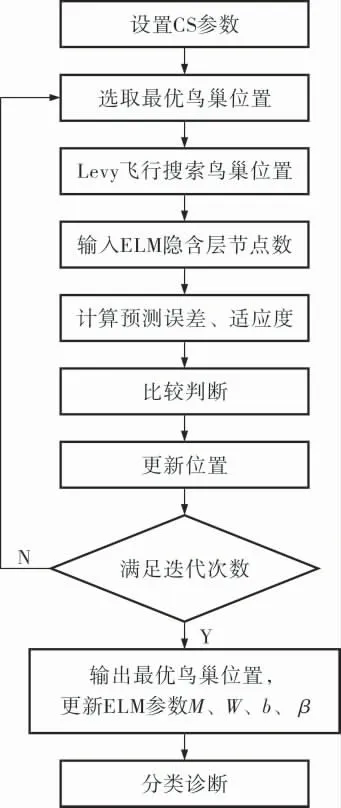
图1 利用CS算法对ELM参数优化的具体流程

3 基于VMD样本熵和CS-ELM的滚动轴承故障诊断实例分析

3.1 滚动轴承故障诊断流程

基于VMD样本熵和CS-ELM的滚动轴承故障诊断流程如图2所示。

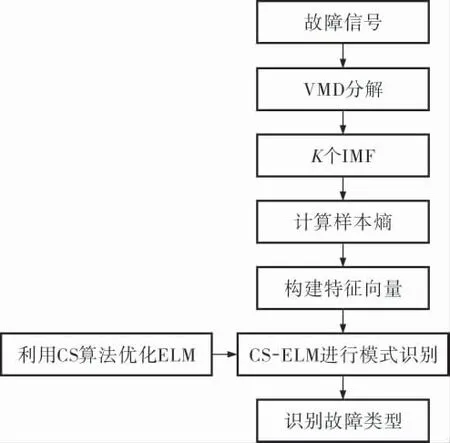
图2 基于VMD样本熵和CS-ELM的滚动轴承故障诊断流程

3.2 滚动轴承实验设置

采用美国凯斯西储大学电气工程实验室采集的滚动轴承数据进行实验分析。 实验轴承为6205-2RS JEM SKF深沟球轴承，轴承损伤直径均为0.177 8 mm，转速为1 797 r/min，采样频率为12 kHz。

滚动轴承正常状态、内圈故障、滚动体故障、外圈故障的振动信号如图3所示， 每个样本的采样点数为6 000。

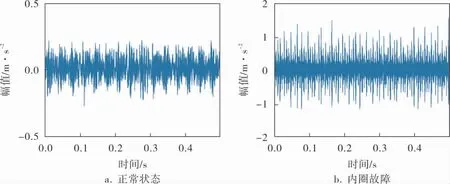
图3 滚动轴承的4种振动信号

3.3 VMD样本熵特征提取

对图3所示滚动轴承的4种振动信号进行VMD分解， 分别得到4个IMF分量， 结果如图4所示。

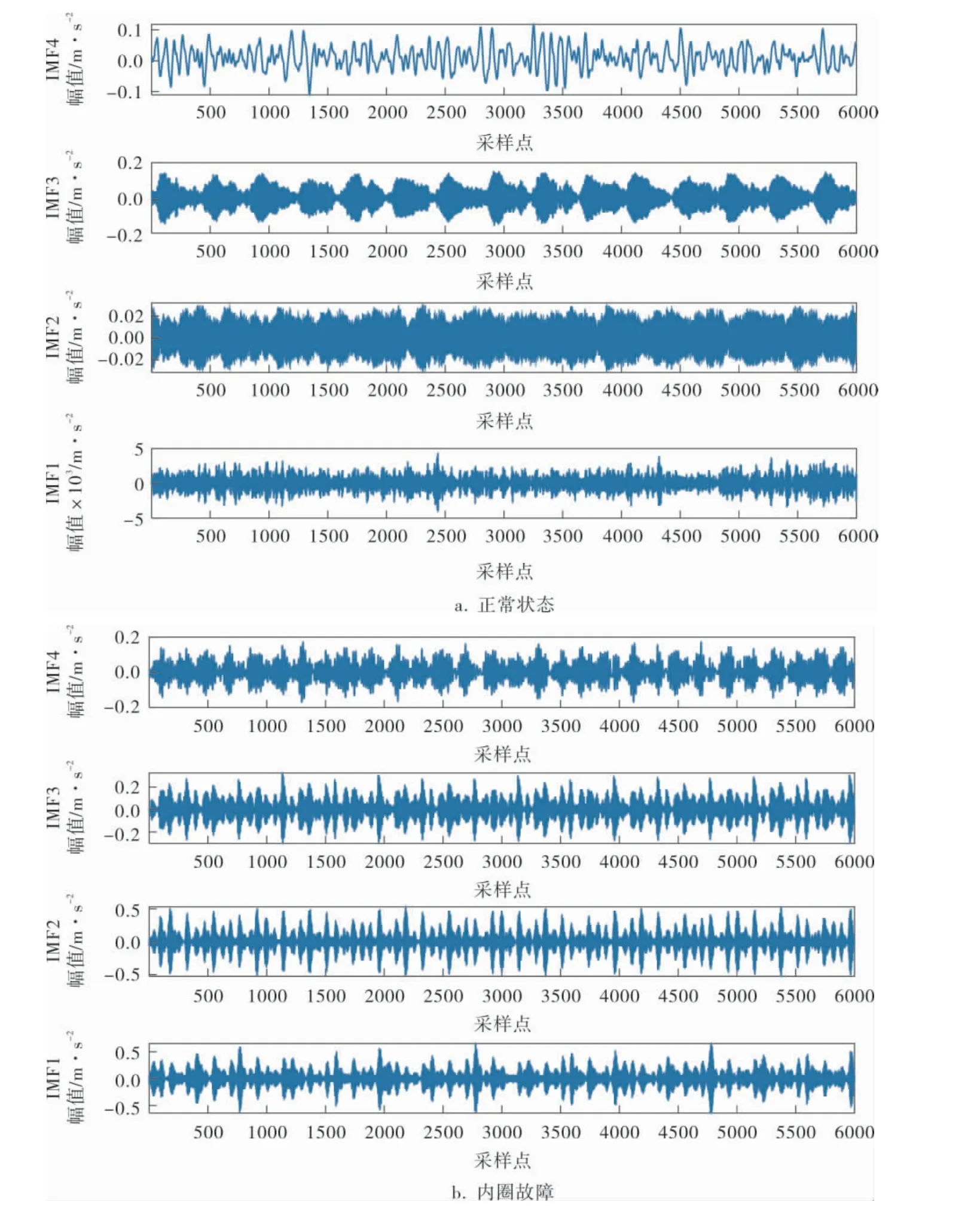
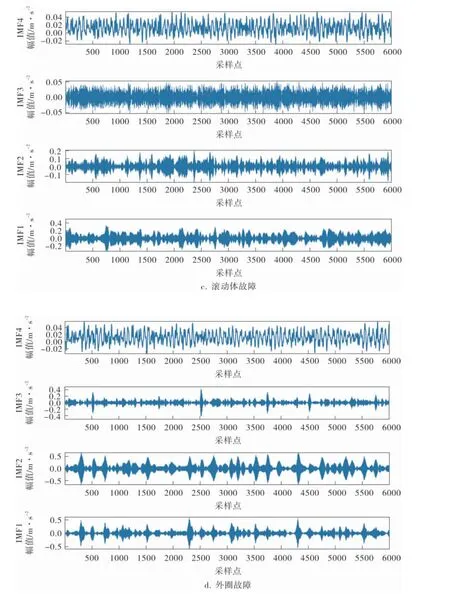
图4 VMD 分解结果

对各模态分量的样本熵进行计算形成特征向量，由于篇幅限制，表1仅列出了4种状态下的部分样本熵特征值。

3.4 基于CS-ELM的故障状态识别

基于CS-ELM的故障状态识别步骤如下：

a. 样本集。 选择表1中每种状态下的特征值各200个组成4个故障特征向量样本，并将样本进行归一化处理。

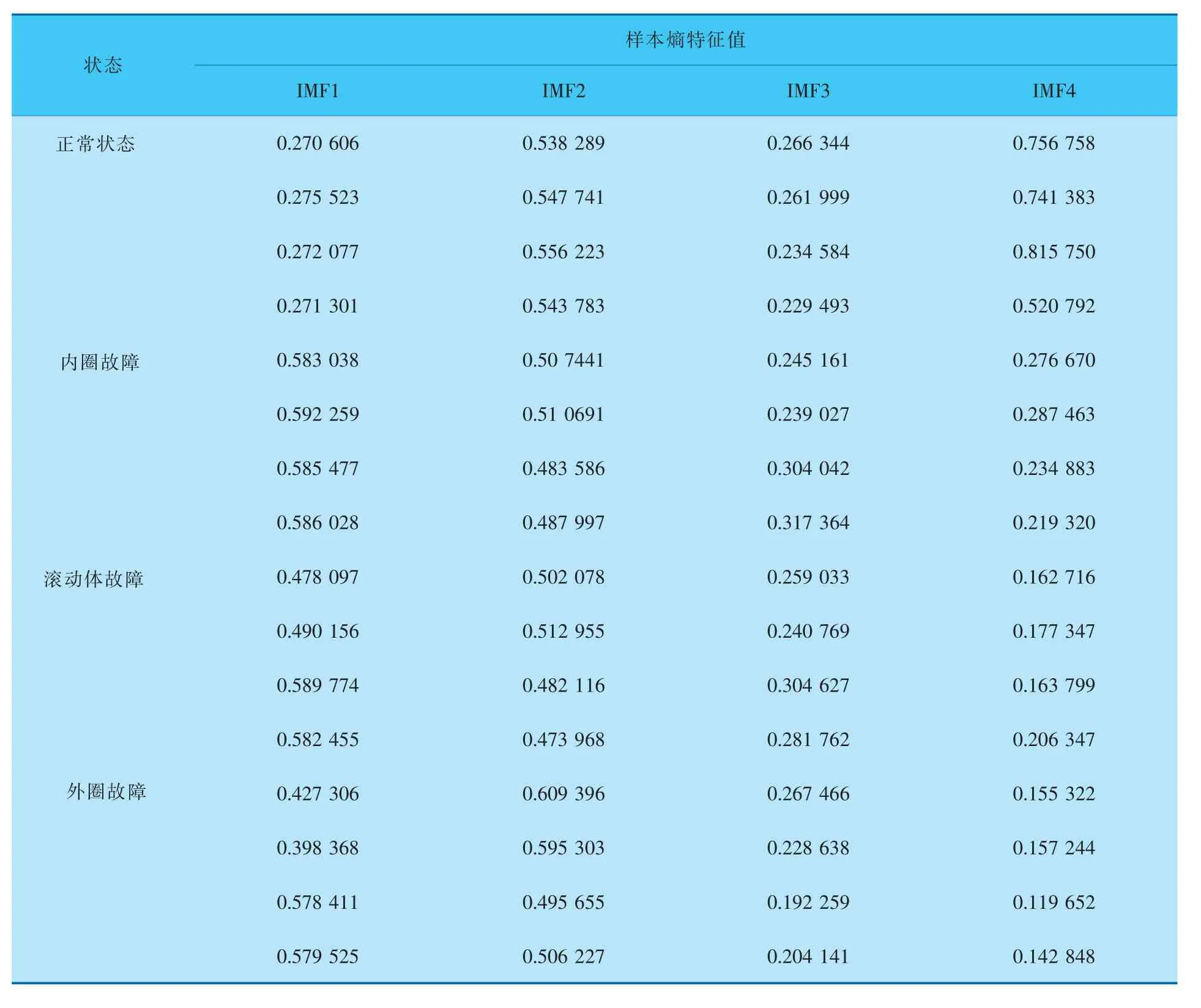
表1 部分样本熵特征值

b. 参数优化。 设置鸟巢规模为30，最大迭代次数为200， 利用CS算法对ELM网络的输入权值和隐含层阈值进行优化，得到最优参数。

c. 故障诊断。 将归一化的样本集输入到CSELM模型中进行训练，其中训练集170个，测试集30个，正常状态、内圈故障、滚动体故障、外圈故障的类别标签分别为1、2、3、4。

ELM和CS-ELM模型的训练、 测试结果如图5所示。从图5可以看出，CS-ELM比ELM分类准确率要高，对比数据见表2。

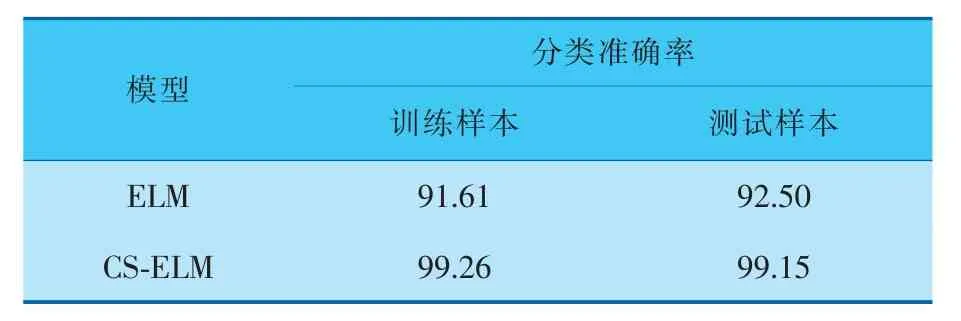
表2 两种模型的分类准确率对比 %

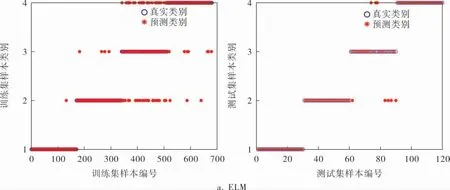
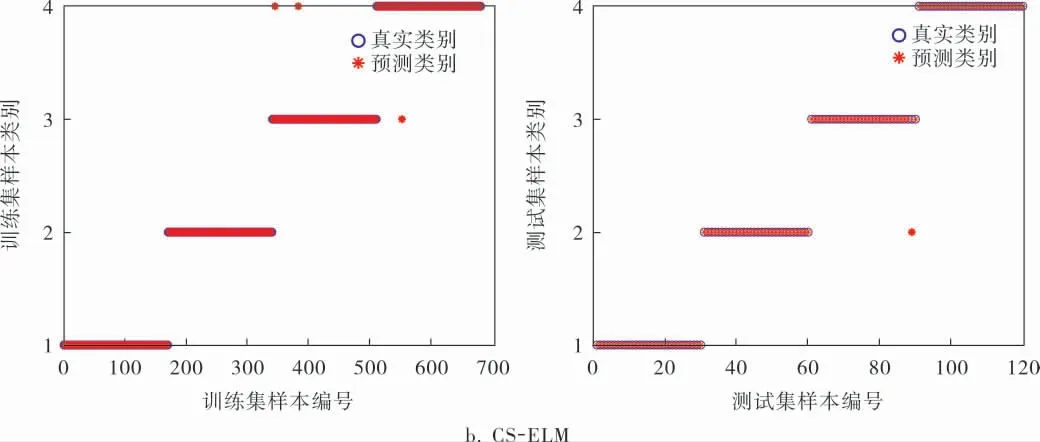
图5 两种模型的训练、测试结果

4 结束语

VMD样本熵能有效表达故障信息，CS算法具有较强的寻优能力， 将VMD样本熵与CS-ELM算法相结合用于提高滚动轴承故障识别的准确率。为证明CS-ELM模型的有效性， 与ELM进行对比，实验结果表明，CS-ELM模型对轴承故障识别的准确率比ELM高， 且鲁棒性更好，CS-ELM模型更有利于滚动轴承故障诊断。