基于最大转矩电流比控制策略的永磁同步电机效率优化研究

魏成坤

（中国石油天然气股份有限公司大庆石化分公司炼油厂）

工业电力中电机的能耗占到很大比重，在国家倡导保护环境和节能减排的背景下，电机系统效率优化具有重要意义［1～3］。 随着永磁体的出现，永磁同步电机发展迅速。 永磁同步电机具有许多良好的特性，如高转矩惯量比、高功率重量比和低噪音，在电动汽车领域，永磁同步电机被广泛使用。

好的控制策略是电机运行效率的保障。 近年来，一些学者对电机控制系统节能方法的研究取得了丰硕的成果，提出了许多新的控制策略。 国外学者提出了损耗模型法［4～6］，在计算时需要准确的电机参数，但实际电机运行状态复杂，模型参数的精度很难保证。 国内学者根据不同运行工况下，电机实现效率最佳的条件不同，提出了曲线拟合法控制策略，推导出不同条件下的最优励磁电流［7～10］，该方法模型复杂且计算难度大。 除此之外，还有恒功率因数法，其控制思路是在给定转速下，如果此时电机损耗是最小的，那么电机的功率因数将保持恒定［11］，但该方法难以保证效率的全局最优，效率优化精度不高。

上述几种方法各有优劣，笔者探索基于最大转矩电流比（MTPA）控制策略的永磁同步电机效率优化方法， 相比于传统的定子电流id=0控制方法，不仅有着突出的转速调节优势，还能大幅降低损耗，提高永磁同步电机的运行效率。

1 永磁同步电机d-q轴数学模型

假设可忽略涡流、磁滞和铜损、正弦反电势、平衡三相绕组和磁饱和问题，可以给出如下永磁同步电机模型的d-q轴电压方程：

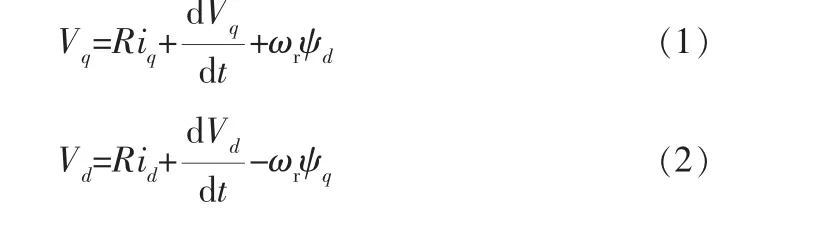
式中 id、iq——d-q轴坐标系下的定子电流；

R——每项的定子绕组电阻；

Vd、Vq——d-q轴坐标系下的定子电压；

ωr——转子角速度；

ψd、ψq——d-q轴坐标系下的定子绕组的磁链。

而且ψd、ψq可以被表示为：

式中 ψm——d-q轴坐标系下的永磁磁链。

这里：

式中 L1——每相的漏感；

Ld、Lq——d-q轴坐标系下的电感；

Lmd、Lmq——d-q轴坐标系下的磁化电感。

转子角速度与定子角速度有关，关系式为：

式中 p——电机极对数；

ωs——定子角速度。

利用式（1）～（7），给出如下数学模型：

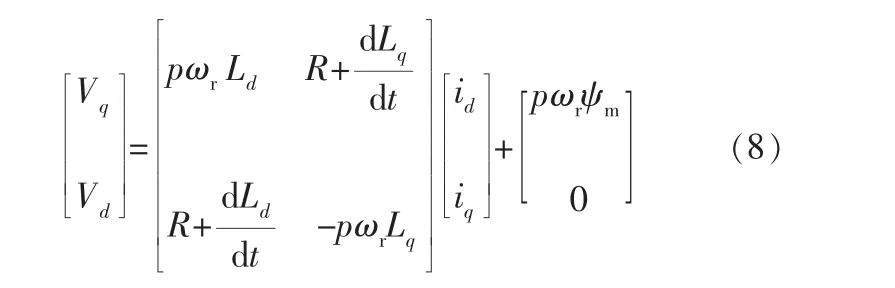
基于式（3）～（8）可以构造出如图1所示的d-q轴等效电路。

图1 d-q轴等效电路

如果以d轴作为参考相量，稳态定子相电压Va可由d-q轴等效电路推导得出：

定子电流is可由id和iq得到：

当设置id为0时， 定子电流is可以通过单独调节iq来控制， 进而让其保持为常数以获得恒定的电磁转矩。 在图1中的每个激励源提供的功率是可以计算的，由于磁饱和、涡流、磁滞和铜损耗都可以忽略不计， 所以输入功率Pi和输出功率Po是一样的：

式中 Bm——摩擦阻尼系数；

J——转子的转动惯量；

TL——负载转矩。

2 永磁同步电机的MTPA控制系统设计

最大转矩电流比控制策略的思路是使用幅值一定的定子电流产生最大的电磁转矩，在该控制方式下所需的定子电流最小，对应的电机铜损耗也最小。 这种控制方法的目的是通过计算找出定子电流与电磁转矩的最佳组合，使在目标电磁转矩下，定子电流幅值最小。

2.1 永磁同步电机电磁转矩模型

控制id、iq便可以控制电机的电磁转矩，而id、iq又是由定子电流的空间矢量的幅值和相位角决定的，即：

式中 Is——定子电流is的幅值；

γ——电枢电流空间矢量与直轴位置的夹角，简称相位角。

永磁同步电机的定子电流经过变换后，电机的电磁转矩表达式为：

采用最大转矩电流比控制策略就是要充分利用电机的电磁转矩，使得单位电流输出最大转矩，提高电机的效率。 采用最大转矩电流比控制时，应满足：

结合id和iq的关系，用iq表示id：

2.2 永磁同步电机最大转矩电流比控制原理

图2 永磁同步电机最大转矩电流比控制原理

3 系统仿真与分析

3.1 系统仿真电路模型

根据所建立的数学模型和理论分析结果，在Matlab仿真环境下，搭建了永磁同步电机基于id=0的传统控制系统和MTPA控制系统的仿真系统。电机参数如下：

定子绕组电阻R 1.09 Ω

转动惯量J 0.000 8 kg·m2

极对数p 3

摩擦系数F 0.000 1

交、直轴电感Ld、Lq0.008 2 H

永磁磁链ψm0.182 7 Wb

铁损电阻Rc108.23 Ω

额定转速Nr1 500 r/min

额定电磁转矩Te5 N·m

3.2 永磁同步电机id=0控制方式和MTPA控制方式的仿真结果与分析

3.2.1 当负载转矩为1 N·m时的仿真及波形分析

图3为id=0控制方式负载转矩为1 N·m时的效率波形，可以看出，刚开始由于电机刚刚启动，所以损耗较大，在0.2 s左右时，效率基本稳定，大约在0.95。 图4为MTPA控制方式负载转矩为1 N·m时的效率波形，可以看出在0.15 s左右，效率基本趋于稳定，而且效率更接近于1.0，大约为0.97。

图3 id=0控制方式负载转矩为1 N·m时的效率波形

图4 MTPA控制方式负载转矩为1 N·m时效率波形

通过id=0控制方式和MTPA控制方式的仿真波形对比，得出MTPA控制方式相比于id=0控制方式， 在负载转矩为1 N·m时， 效率提高了2%。

3.2.2 转速变化时的仿真及波形分析

仿真过程中，让转速在0.6 s时由1 kr/min变化为1 500 r/min，id=0传统控制方式和MTPA控制方式仿真结果分别如图5、6所示。 id=0控制方式的损耗在0.65 s左右恢复，MTPA控制方式的损耗在0.63 s左右恢复。 对比两种控制方式的波形，可以明显地发现MTPA控制方式的恢复速度超过id=0方式的恢复速度，由于转速变化时和启动时损耗更大， 最大转矩电流比控制方式动态性能更好，所以损耗进一步降低。

图5 转速变化时id=0控制方式的损耗波形

3.2.3 负载转矩变化时的仿真及波形分析

仿真过程中，0.5 s时突加负载转矩2.5 N·m，id=0控制方式和MTPA控制方式的仿真结果分别如图7、8所示。 对比两种控制方式的波形可以发现，MTPA控制方式转矩跟随性较好，而且在突加负载转矩时，有着更快的响应能力。

图6 转速变化时MTPA控制方式的损耗波形

图7 负载转矩变化时id=0控制方式的转矩波形

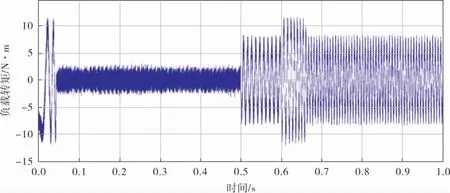
图8 负载转矩变化时MTPA控制方式的转矩波形

4 结束语

永磁同步电机具有诸多优点，在许多领域得到了越来越广泛的应用。 但是永磁同步电机在运转的过程损耗较大，还具有极大的节能空间。 笔者提出了基于MTPA控制方式的永磁同步电机效率优化方法。 将其与id=0控制方式分别进行了负载转矩为1 N·m、 转速变化和转矩变化时的仿真对比分析， 结果表明MTPA控制方式相比于传统的id=0控制方式不但降低了损耗， 改善了系统的动态性能，还提高了系统运行的效率，拓展了效率优化的区间。