缺失数据下基于改进PLS方法的质量相关故障检测

2021-09-24朱守博赵忠盖

化工自动化及仪表 2021年5期

朱守博赵忠盖刘飞

（江南大学物联网工程学院轻工过程先进控制教育部重点实验室）

在现代工业过程中，多元统计过程监控（MSPM）方法得到了广泛应用，包括基于主成分分析（PCA）［1］、偏最小二乘（PLS）［2］及典型变量分析（CVA）［3］等监控方法。其中，基于PCA的故障检测与诊断技术能够有效地检测过程变量，但是根据过程变量与质量变量间的相关关系判断质量指标和过程运行状态更为重要［4］。 CVA的建模目标是使两组变量间的相关系数最大化，而PLS则寻求两组变量之间的协方差最大化。 PLS集合了CVA和PCA的基本功能，在质量相关的故障检测领域获得了大量的成功应用［5，6］。

PLS的目的是提取过程变量和质量变量的特征信息，并使两者间的相关性最大［7］。因此，过程变量的主成分中可能包含了大量与质量变量无关的信息，同样地，质量变量的主成分中也可能包含了大量无法由过程变量估计的信息［8］。另一方面，PLS不像PCA那样以降序的方式提取输入空间中的方差。因此，残差中可能会包含大量的有用信息，并不符合采用Q统计量进行监控的条件［9］。

为了解决以上问题，高效潜结构投影（EPLS）方法将过程数据分解为质量相关部分和质量无关部分，并使用PCA对质量无关部分做进一步分解，保证空间分解的完备性。EPLS模型最终生成3个子空间：质量相关子空间、质量无关子空间和残差子空间［10］。其中质量相关子空间对输出的预测有全部贡献，质量无关子空间包含与输出正交的部分，残差子空间只包含过程数据的干扰或噪声。基于EPLS模型，监控方法可以对上述3个子空间的信息分开进行评估，提高了故障检测的准确率。

另一方面，在实际的工业过程中，由于传感器故障、格式错误及非代表性采样等原因，很多样本数据往往不完整，给数据驱动建模带来了挑战［11］。迭代算法（IA）是一种常用的解决缺失性难题的手段［12，13］。 Smirnov M Y等将PCA和PLS分别集成到IA方法中实现对缺失数据的建模［14，15］。笔者引入IA算法，提出一种缺失数据下的EPLS算法——IA-EPLS。该方法通过不断地迭代完成EPLS建模：用估计的缺失数据建立EPLS模型，然后基于该EPLS模型重新估计缺失数据。两个步骤交替迭代进行，直到收敛，即可得到EPLS模型和重构数据集。笔者还将该方法应用到故障检测中，构建EPLS生成的3个子空间的监控指标，通过一个数值仿真和田纳西伊士曼（TE）过程仿真证明该方法的有效性。

1 PLS和EPLS

1.1 PLS模型

PLS的目的是提取过程变量和数据变量的主元，并使两者的相关性最大。假设给定过程数据矩阵X∈RN×m，质量数据矩阵Y∈RN×p（其中，N为样本数，m为过程变量数，p为质量变量数）。用非线性迭代偏最小二乘法（NIPALS）将（X，Y）投影到低维空间：

其中，T=［t1，t2，…，tA］为得分矩阵；P=［p1，p2，…，pA］和Q=［q1，q2，…，qA］分别是X和Y的负载矩阵；A为PLS的主元个数，通常由交叉验证确定；E和F分别对应X和Y的残差。

在NIPALS算法中，将W=［w1，w2，…，wA］定义为权重矩阵，由于无法直接由原始过程数据X得到T，所以引入R=［r1，r2，…，rA］，满足T=XR，且有：

基于PLS的监控通常使用T2和Q统计量。对于一个新的样本xnew，可计算其得分tnew和相关统计量：

1.2 EPLS

PLS通过两个子空间对过程进行监控仍然会面临一些问题。原因在于：主元子空间仍然包含与Y正交的部分，这不利于检测；PLS强调了X对Y的解释作用，并没有在过程变量矩阵中按方差降序提取主成分。为了解决这些问题，EPLS首先将过程空间分解为两个正交子空间：与质量相关的子空间X^ 和与质量无关的子空间X～。其中质量相关子空间不包含正交Y的成分。其次，对X～进一步进行主元分析，产生质量无关子空间和残差子空间。

EPLS模型如下：

EPLS算法将过程数据空间分解地更加简洁和完整。

2 基于IA-EPLS 的质量相关故障检测方法

2.1 IA-EPLS模型

考虑过程变量数据中包含缺失项：

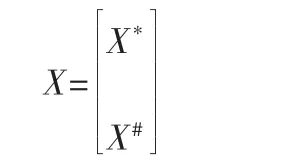
其中，X#表示缺失的测量数据，X*表示观测到的测量值。相应地，系数矩阵M的计算式为：

因此，系数矩阵M仅由X*决定。在EPLS建模中，如果过程变量出现缺失数据，则该变量所在的所有测量值均无法用于建模，导致大量过程数据信息丢失，甚至无法准确建立模型。在IA-EPLS中，IA的中心思想是在每次迭代中估计缺失的值。 IA的每次迭代由两步组成。在初始化缺失数据（通常为零，或对应列的已知值的均值，或对应行和列的均值）后，第1步根据实际数据估计出模型参数；第2步，利用现有模型的实际数据和参数，计算缺失数据的期望值。 IA的收敛准则是连续两次迭代过程中缺失数据的估计值小于一定的阈值。 IA-EPLS算法的步骤如下：

a. 按行和列的均值初始化缺失数据；

b. 初始化X和Y；

c. 计算系数矩阵M；

i. 从初始X和Y中减去缺失部分的估计值，计算误差平方和，然后除以缺失采样的个数；

j. 如果计算结果小于指定的阈值，如10-4，则满足收敛条件，转向步骤k，否则转向步骤b；

在上述算法中，用EPLS模型得到的期望值填补缺失数据，构建新的数据集，并拟合新的EPLS模型。迭代结束后，得到最终的模型可以表示为质量相关和质量无关部分：

2.2 基于IA-EPLS的故障检测方法

3 仿真分析

3.1 数值案例

其中，ξ和f分别为故障方向变量和故障大小。

采用500个正常工况下的采样数据建立IAEPLS模型：设置缺失数据分别为样本的10%、20%和30%，随机分布在输入数据和输出数据中。另有验证数据500个样本，其中前250个采样点为正常数据，后250个样本为故障数据。基于IA-EPLS方法的检测结果如图1所示（红线为阈值）。

图1 缺失数据占比为10%、20%和30%下基于IA-EPLS的故障检测结果

3.2 TE过程实验

TE过程是一个开放的仿真系统，被广泛用于过程监控方法的验证研究中［18～20］。 TE过程由5个操作单元组成：化学反应器、冷凝器、压缩机、汽液分离器和汽提塔，包含41个过程变量（XMEAS（1～41））、12个控制变量（XMV（1～12））和21种故障类型（IDV （1～21））［21，22］。选择22个过程变量（XMEAS（1～22））和11个控制变量（XMV（2～12））作为输入矩阵X；过程变量XMEAS（35）作为输出变量［23］。每个测试样本经过960次采样，其中故障在第161个样本处引入，训练数据集由正常工况下的500个样本组成。在仿真中，一定比例的缺失数据被添加到训练数据集中。由于在实际情况下，缺失数据通常是未知的，常用的填补方法是均值填补法，因此训练数据集中缺失的元素被视为零。

图2 缺失数据占比为20%下基于IA-EPLS的故障检测结果

为了便于比较，EPLS方法用平均值替换缺失数据实现最终的监控模型。该部分共设计3组仿真实验，缺失数据的比例分别为10%、20%和30%。基于IA-EPLS和EPLS方法对故障IDV（1）的检测结果分别如图3、4所示（红线为阈值）。从两图中可以看出，缺失数据下基于IA-EPLS的故障检测方法比EPLS效果更好。随着缺失数据比例的增加，基于IA-EPLS的方法保持了较高的故障检测率（FDR），而基于EPLS方法的故障检测率逐渐降低。此外，在表1中总结了不同缺失数据比例下两种方法的FDR。