基于聚类分析和信息熵的灰色关联分析在便携式呼吸机采购决策中的应用研究

孙 鹏

（北京急救中心，北京 100031）

0 引言

2020年，全球新型冠状病毒肺炎（以下简称“新冠肺炎”）疫情暴发，因其传播速度快、传染性强，国家卫生健康委员会将新冠肺炎纳入乙类传染病，按甲类传染病管理[1]。呼吸机是抢救和治疗各种原因引起的急慢性呼吸衰竭的必备工具，新冠肺炎疫情期间，呼吸机在院前危急重症患者监护和急救转运过程中更是起到至关重要的作用。呼吸机性能的好坏关系到患者的生命安全，同时为保证采购的呼吸机达到较好的技术效益、经济效益和社会效益，需要对其配置进行合理选型。笔者结合个人工作内容及单位实际需求，以便携式呼吸机采购选型为研究内容，在不属于政府采购范围的前提下，探讨一种新的细化选型指标模式及采购方法路径，避免选型指标权重设定和产品采购主观性过强的问题。

1 呼吸机评价指标

呼吸机种类繁多，产品的采购首先要审核呼吸机及供应商的相关资质，即完全符合国家技术质量规范和该产品规格、性能等要求，然后在此基础上要制订一个比较完备的呼吸机评价指标体系，用来评价呼吸机系统的指标参数。呼吸机评价指标涉及的因素很多，结合多个招评标文件的采购需求、专家综合评分以及市场产品调查，笔者简要总结，细化分为以下指标：通气功能（X1）、通气模式（X2）、核心参数（X3）、驱动方式（X4）、价格优势（X5）、售后服务（X6）、整机质量（X7）、销售业绩（X8）。

1.1 通气功能

不同呼吸机有不同的通气功能，同一型号的呼吸机从无创通气到有创通气，其适用患者范围更广、治疗方式更多、选择模式更多。同一呼吸机具备2种通气功能不仅可以更好地应对患者的病情变化，并且可以减少购买呼吸机的数量[2]。

1.2 通气模式

通气模式应满足婴幼儿、成人和通用多种使用需求，并且多种通气模式与有创、无创通气功能结合可使呼吸机治疗功能发挥最优的效果。市场上有些呼吸机虽然兼具有创和无创通气，但由于通气模式单一，有创通气的功能弱化，不能较好地满足临床使用要求。因此，通气模式也是一个重要指标。

1.3 核心参数

核心参数包含基础参数和高级参数，基础参数可以动态掌握患者的呼吸力学改变，高级参数在基础参数的支持下可用来制订个体化的通气策略。市场上呼吸机产品多、性能优劣差异大，为适应各种严峻急救环境，保证急救的安全性，需要呼吸机性能稳定（如完善的警报系统和自检系统，可提高治疗安全性），以实现院前、院内有效衔接。特别是潮气量、通气频率等基础参数设置范围大，医护人员可结合患者病情动态调整设置参数。此外，具有压力、流量和CO2监测功能的呼吸机可输出呼吸波形，有利于医护人员根据患者病情及时调整呼吸机波形参数值[3-5]。

1.4 驱动方式

呼吸机按驱动方式一般分为气动电控呼吸机和电动电控呼吸机。目前本中心所选用的是以压缩气体作为动力源的气动电控呼吸机，主要原因是院前急救在院外进行，采用气动电控呼吸机可避免电动电控呼吸机涡轮机在飞机或急救车上由于道路颠簸对使用带来的影响。此外，还能够满足现代多种呼吸模式的需要。

1.5 价格优势

价格是影响呼吸机选择的重要因素。采购方注重呼吸机的经济效益，因此呼吸机价格应具有竞争力。应综合考虑呼吸机性能、产品质量和售后服务等因素，选出更具价格优势的呼吸机[6]。

1.6 售后服务

售后服务是对产品的风险管理，可采取措施将呼吸机在院前使用的风险控制在可接受水平，如定期更换空气过滤棉、常规维护和安全检查、更换损耗部件等，因此将售后服务确定为呼吸机评价的重要指标[6]。

1.7 整机质量

体积小、质量轻的呼吸机在院前急救与转运过程中可减轻医护人员负重，使医护人员快速到达救援现场，以及时救治伤者。因此，在设定评价指标时也要考虑呼吸机的整机质量。

1.8 销售业绩

呼吸机销售业绩高低往往反映着市场满意度，这与呼吸机性能、质量、售后服务等密切相关。因此，本研究将呼吸机销售业绩作为一项重要指标。

当前呼吸机采购过程中的评价标准大多比较笼统，例如采用价格模块、商务模块、技术模块以及售后服务模块四大模块。此评价指标初步引入了权值的概念，容易对照标准“打分”。但是仍难以细化核心参数指标，精确到每一个分数值，难以合理界定评价因素及权值，难以找出技术和价格等标准分值之间的平衡关系。

本文将产品技术参数指标进行合理细化，有利于评价出技术性能出色的呼吸机，且能够充分考虑使用价值，更合理地赋予各项指标权值，避免一定的主观性采购。

2 数学模型

2.1 聚类分析方法

聚类是将数据对象的集合分成相似对象类的过程。同一类中的对象之间具有较高的相似性，而不同类中的对象具有较高的相异性。

聚类分析方法包括层次法（对给定数据对象集合进行层次的分解）和自底向上（层次凝聚）方法。自底向上方法也称为聚合层次法，该方法以最初每个点作为一个类（原子类），每一步合并2个最相似的类。这种方法需要定义类的相似性度量和算法终止的条件。

本研究对呼吸机分类时采用自底向上的聚类方法。假设评价对象i有n个，纳入的评价指标j有m个，则n个评价对象的m个评价指标数据集可以构成评价矩阵xij[7]：

为计算评价对象间的相似度（即距离值），先设置度量距离值dist（xi，xj），然后采用欧几里得公式得到度量距离（欧式距离）：

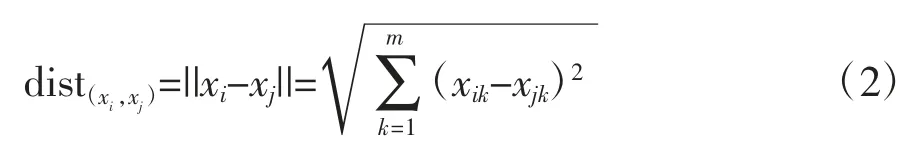
欧几里得距离函数通常满足以下性质：

（1）非负性，dist（xi，xj）必须是一个非负数。

（2）某个对象到自己的距离为0，即dist（xi，xj）=0。

（3）对称性，dist（xi，xj）=dist（xj，xi）。

（4）满足三角不等式，即dist（xi，xj）≤dist（xi，xk）+dist（xk，xj）[8]。

先将所有单独样本看成一类，采用公式（2）求出每一类的相互距离，得出距离矩阵，将矩阵中的每一个数值按照升序进行排列。根据排好的序列合并最靠近的2类（因为它们具有最小的类间距离），得到新的类集合后，更新距离矩阵，再次进行合并最靠近的2类，更新距离矩阵，直到达到设置的收敛条件，得出结果。

2.2 采用熵权法求呼吸机每项指标的权重

熵权法是一种在综合考虑各因素提供信息量的基础上计算一个综合指标的数学方法。作为客观综合定权法，其主要根据指标变异性的大小来确定客观权重。

计算权重的熵值，其作用并不是评价某个评价指标的实际熵值（信息量）大小，而是体现对应评价指标在给定的评价体系中的作用，反映评价指标的相对重要性。从信息论的角度来看，它代表该问题中有用信息的多寡程度。指标的信息熵Ej越小，表明指标值变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，其权重也就越大。相反，指标的信息熵Ej越大，表明指标值变异程度越小，提供的信息量也越少，在综合评价中所起到的作用也越小，其权重也就越小。

为计算各项指标的权重，须选取n个样本，m个指标，xij则为第i个样本的第j个指标的数值。对指标进行标准化处理，归一化后的数据记为xij'，其表示形式为

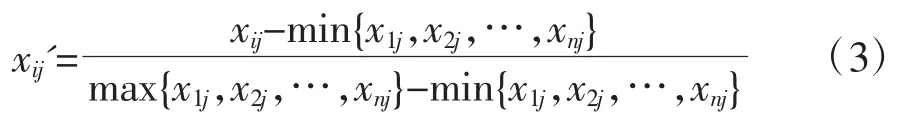
计算第j个指标下第i个样本指标属性的贡献度pij，计算公式为

从信息传播的角度来看，信息熵可以表示信息的价值。可衡量所有样本对第j个指标的贡献标准Ej，其计算公式为

最后通过公式（6）计算各个指标的权值wj，计算各样本的综合得分，选择待评价产品类。wj计算公式为

2.3 采用灰色关联分析法对待评价产品类进行综合分析

采用灰色关联分析法对待评价产品类进行综合分析时，在灰色系统中，呼吸机各项参数与最优对象的关系是不确定的。为显示备选产品与最优对象的关联关系，需要确定一个表示关联程度的量，这里称作关联系数。灰色关联分析法是进行关联分析的，并非评价分析。进行灰色关联分析时，须首先关联一个虚拟最优对象，与虚拟最优对象关联系数最大的，即为最优解。该虚拟最优对象的参考数据列是一个理想的比较标准，可以以各指标的最优值（或最劣值）构成参考数据列，也可根据评价目的选择其他参照值，记作x0。该数据集包含8项指标，记作x0（j），其计算公式如下：

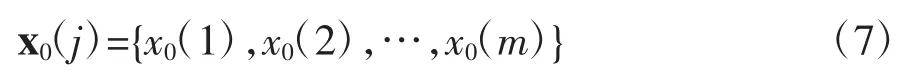
为比较备选产品与虚拟最优对象间的差距，首先逐个计算每个待评价对象指标序列（比较序列）与参考序列对应元素的绝对差值，即确定数据列的最大值和最小值

其次根据数据列的最大值和最小值计算关联系数ξi（j）：

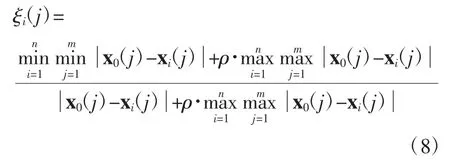
式中，ρ为分辨系数，0<ρ<1。ρ越小，关联系数间差异越大，区分能力越强。通常ρ取0.5。

最后计算关联序。对各评价对象（比较序列）分别计算其指标与参考序列对应元素的关联系数平均值，以反映各评价对象与参考序列的关联关系，并称其为关联序。因为指标在综合评价中所起的作用不同，可对关联系数求加权平均值ri，计算公式为按关联系数的大小排序，组成关联序，得出最优呼吸机产品。

3 举例分析

通过举例来对本研究提出数学模型进行分析说明。设A～J为10种不同品牌的呼吸机，对10种不同品牌的呼吸机的各个指标进行赋值，由高到低依次设为4个级别的赋值标准：9、8、7、6，详见表1。

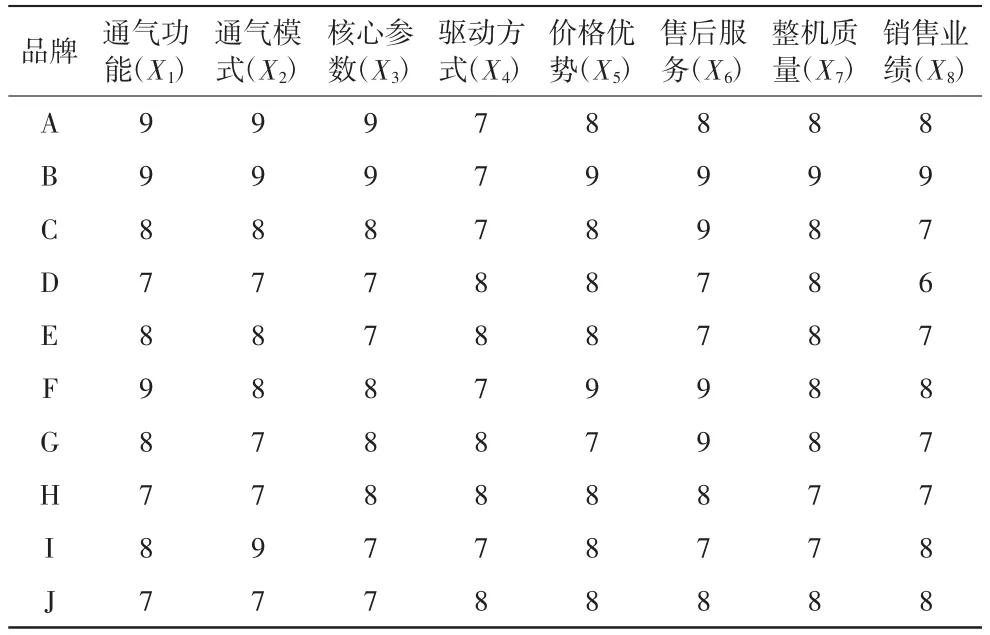
表1 呼吸机评价指标赋值表

3.1 聚类分析

（1）计算欧式距离。

对10种品牌呼吸机进行聚类分析，使得同一类中的对象之间具有较高的相似性。根据本研究指标值，设相似度距离为2。先将10种品牌的呼吸机分别看成一个类，采用公式（2）计算各类两两之间的距离。因为本文数据较少，采用人工计算，得出对称距离矩阵，详见表2。

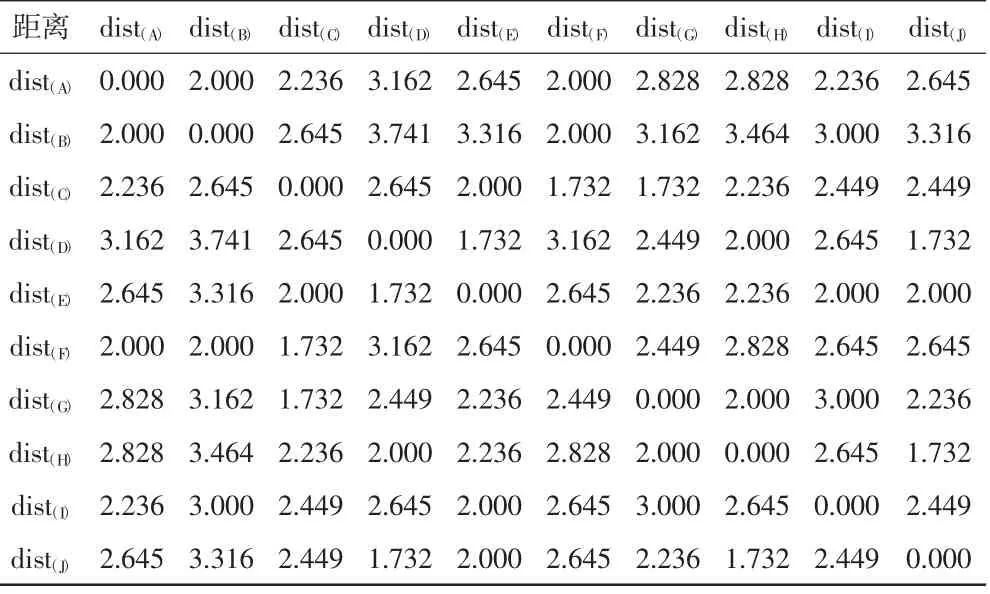
表2 10种品牌呼吸机两两距离矩阵表

（2）聚类。

找到最小的类间距离，合并距离最小的2类，直到达到收敛条件。最终分为3类：第一类呼吸机为A、B、C、F，第二类呼吸机为D、E、I，第三类呼吸机为H、J、G。通过聚类分析得出3类呼吸机对比分析结果如下：

第一类呼吸机：通气功能、通气模式、核心参数、售后服务、销售业绩比较高的一类呼吸机。

第二类呼吸机：驱动方式优于第一类呼吸机，通气模式优于第三类呼吸机，通气功能、核心参数、整机质量与第三类呼吸机相似。

第三类呼吸机：驱动方式优于第一类呼吸机，核心参数、售后服务优于第二类呼吸机。

3.2 根据熵权法求呼吸机每个指标的权重

（1）标准化处理。

对各个指标的数据进行标准化处理。通过公式（3）计算各指标数据标准化后的值，详见表3。

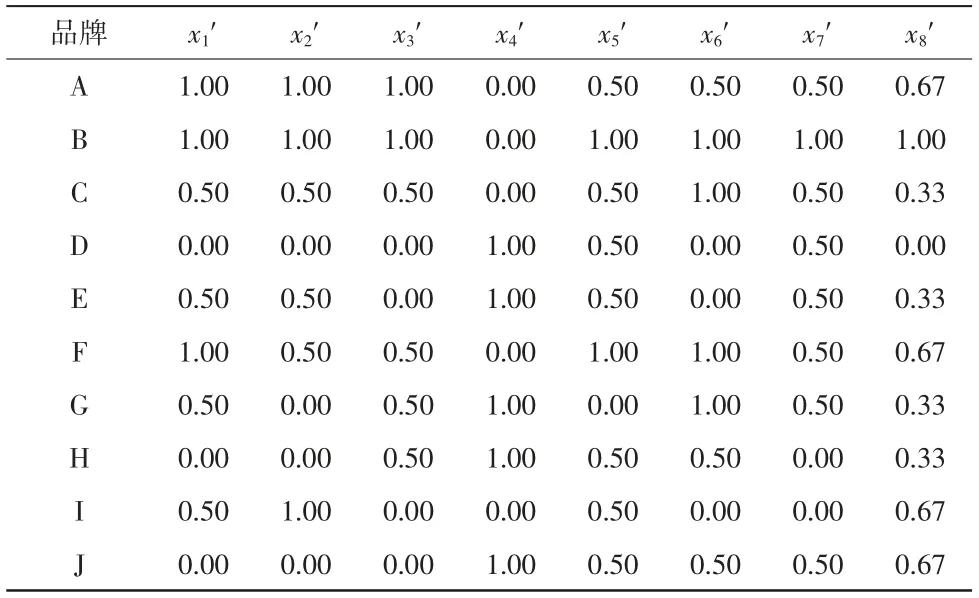
表3 呼吸机评价指标标准化数据值

（2）计算指标贡献度。

通过公式（4）计算第j个指标下第i个样本指标属性的贡献度，详见表4。

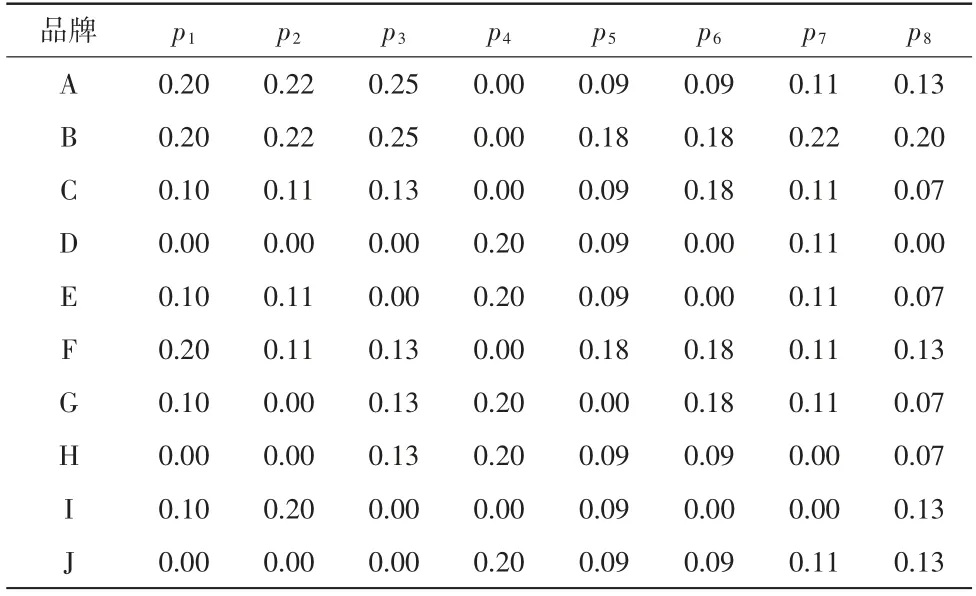
表4 指标贡献度

（3）求信息熵。

通过公式（5）求各指标的信息熵，X1、X2、X3、X4、X5、X6、X7、X8的Ej分别为0.82、0.75、0.76、0.70、0.92、0.82、0.88、0.93。

（4）计算权重。

通过公式（6）计算各指标的权值，X1、X2、X3、X4、X5、X6、X7、X8的wj分别为0.13、0.18、0.17、0.21、0.06、0.13、0.08、0.05。

（5）计算得分。

为筛选出优秀的一类呼吸机，应计算每一类呼吸机中8项指标得分的平均值，从而得到最终得分。3类呼吸机每项指标平均得分见表5。

表5 3类呼吸机评价指标得分表

根据表5中的数据计算，第一类呼吸机最终得分为8.28，第二类呼吸机最终得分为7.50，第三类呼吸机最终得分为7.63。因为第一类呼吸机最终得分最高，所以选择第一类呼吸机作为待评呼吸机。

3.3 利用灰色关联分析对第一类中所有呼吸机进行综合分析

（1）确定参考数据列。

因为各项指标均为效益性指标，分值越高说明呼吸机该项指标性能越高，根据表1中数据可得各项指标最高分值x0=9、9、9、8、9、9、9、9。

计算|x0（j）-xi（j）|，结果用yj表示。详见表6。

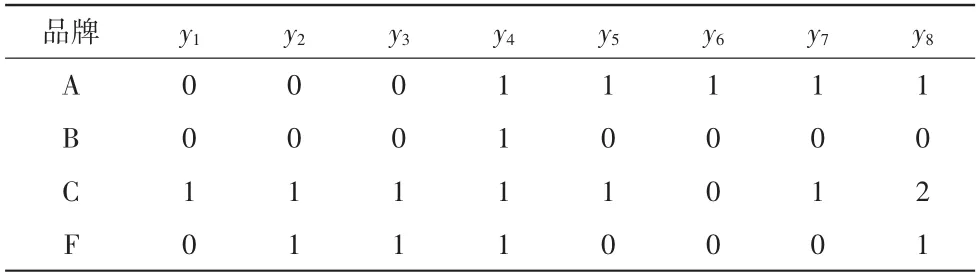
表6 评价指标序列与参考序列绝对差值表

（2）求最值。

（3）计算关联系数。

依据公式（8），ρ取0.5，计算关联系数。详见表7。

表7 关联系数

（4）计算关联系数的均值。

分别计算第一类中每种品牌呼吸机各指标关联系数的均值（关联序），即

（5）关联系数排序。

按上述关联系数的大小排序，即B>A>F>C，得出最优呼吸机品牌为B。

4 讨论

关联序中某一种品牌呼吸机与本研究设想最优的呼吸机越接近，关联系数就会比较大。B品牌呼吸机关联系数最大，所以B品牌呼吸机为最优呼吸机。文中B品牌呼吸机被选中，除了X4指标外，其余各项指标均达到9分，佐证了本研究的评价指标具有实际价值。通过关联系数比较和最终计算结果分析，验证了该数学模型的合理性和准确性，具有实践意义。

第一类待评价呼吸机中，A品牌呼吸机和F品牌呼吸机的总得分相等，但是经过数学模型计算后，A品牌呼吸机的得分高于F品牌。从表1可以看出，A品牌呼吸机的通气模式和核心参数2项指标均比F品牌的得分高，说明购买中高端便携式呼吸机时，这2项指标是更为专家看重且起到决定性作用的。综上，基于聚类分析和信息熵的灰色关联分析法建立的数学模型可以较好地对呼吸机进行评价，这也对以后的呼吸机采购起到一定的实际指导意义。

为验证以上2点结论的有效性，本研究对数学模型再次赋值，相较于上文中赋值总分结果不同的情况，假设8项指标的10种品牌呼吸机赋值总分相等。通过对比分析发现，通气功能、通气模式、核心参数、驱动方式4项指标分值较高且较其他指标相对重要，指标值的离散程度高导致权重较大，能够得出最优类呼吸机组。最优类呼吸机的大部分指标分值较高，结合权重后，关联系数值大的呼吸机最终胜出。所以再次证明数学模型在分值相同的情况下，依然能选出最优呼吸机，也反映了利用该数学模型甄选呼吸机的优势。此外，最终胜出的呼吸机价格优势指标值都不是最低分，而且价格优势指标权重处于8项指标权重中的中等水平，所以该数学模型可以计算出性价比相对较高的呼吸机。

5 结语

运用本文提出数学模型进行众多产品选择时，应首先进行聚类分析，筛选出优秀的一类呼吸机，以减少繁重的计算工作量，提高效率。在聚类分析中，呼吸机评价指标设定的主观性较强，引入信息熵可使评价指标设定更客观。因此基于聚类分析与信息熵的灰色关联分析法建立的数学模型所选出的最优呼吸机具有更高的可信度。此外，该数学模型也适用于其他产品的采购，并不局限于采购呼吸机。

这种通过数学模型得出最优产品的方法对指标权重设定虽然有一定的合理性，但也需要注意该数学模型还有进一步优化的可能，同时在指标选型和权重设定方面还有一定的局限性和主观性。在对待评产品分类和评价方法选择上有很多方法，每种方法都有自己的优缺点，需要针对具体的问题进行设计，尤其在产品评价指标权重的设定问题上有待进一步的研究。