一种电磁-气动式准零刚度隔振器设计与分析

谢英江，牛 福，孟令帅，赵万卓，孙景工

（军事科学院系统工程研究院，北京 100166）

0 引言

救护车辆在伤病员后送过程中搭载的担架、座椅等易受到外界振动的干扰，对伤病员的乘卧舒适性及紧急救治带来很大的挑战，其中低频振动危害更加难以解决[1]。被动隔振器作为振动控制的重要手段，广泛应用于工程领域中，然而只有当外界激励频率大于隔振器固有频率的倍时隔振系统才具有较好的隔振效果[2]。为了降低隔振起始频率，必须降低系统的固有频率，即减小系统刚度，但静态承载能力随之降低，稳定性变差。为提高低频隔振性能，由提供正负刚度的机构并联形成的准零刚度（quasizero stiffness，QZS）隔振器逐渐成为研究热点。准零刚度隔振器在静态平衡位置附近兼具高静态支撑能力和低动态刚度，能够降低隔振系统的起始隔振频率，实现低频甚至超低频隔振。

准零刚度隔振器的种类很多，Alabuzhev等[3]在1989年出版了第一本有关准零刚度隔振器的书籍，系统地阐述了准零刚度的理论和设计方法。Carrella等[4-6]对倾斜弹簧和垂直弹簧并联实现准零刚度特性的隔振器进行了深入研究。Deng等[7]通过模拟鸟颈多椎骨结构和注视稳定性，提出了由三弹簧结构的准零刚度隔振器组成多层准零刚度隔振系统。Zhou等[8]先将V型杆与板簧并联获得非线性负刚度，再与螺旋弹簧并联实现准零刚度。Zhou等[9]和Ye等[10]将凸轮滚子机构和线性弹簧并联，得到了良好的隔振效果。Yuan等[11]利用3个环形线圈与环形磁体同轴排列形成的电磁弹簧与线性弹簧并联实现准零刚度。Liu等[12]利用磁环和电缆设计了一种能够隔离水平面内任意方向振动的隔振器。Jiang等[13]设计了一种磁气混合的准零刚度隔振器，当载荷变化时，隔振器仍然能够保持准零刚度特性。此外，利用开槽碟形弹簧对合组合方式也能实现准零刚度特性[14]。现阶段大部分准零刚度隔振器是通过将负刚度机构和螺旋弹簧并联实现的，结构复杂、体积大，且当隔振质量发生变化时隔振器难以采取应对措施，隔振器的刚度不再趋近于零，低频隔振性能下降。本研究通过将气动弹簧和电磁弹簧并联，设计一种新型结构的电磁-气动式准零刚度隔振器，由气动弹簧提供正刚度，电磁弹簧提供负刚度，结构简单，且通入不同电流和气压时，正负刚度大小会发生改变，为隔振器应对不同隔振质量提供了可能性。

1 准零刚度隔振器模型

电磁-气动式准零刚度隔振器由提供正刚度的双气室气动弹簧和采用吸引配置产生负刚度的电磁弹簧并联得到，其中电磁弹簧对称布置在气动弹簧中心轴线两侧。此外，隔振器还包括套筒、锁紧螺母、导柱、双头螺柱和连接件等其他元件。电磁-气动式准零刚度隔振器结构如图1所示。

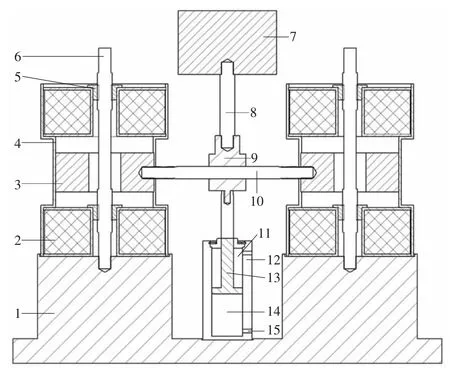
图1 电磁-气动式准零刚度隔振器结构图

电磁弹簧是隔振系统的负刚度机构，由1对线圈绕组和1个环形磁体同轴排列组成，其中线圈绕组用锁紧螺母固定。当线圈绕组加载电流后，线圈和环形磁体之间互相吸引，从而产生负刚度。隔振器两侧的环形磁体通过双头螺柱连接在一起，保证其同时运动。线圈绕组与环形磁体安装在套筒内且环形磁体可在套筒内垂直自由滑动。气动弹簧是隔振系统的正刚度机构，由双气室的压力缸和活塞杆组成。电磁弹簧和气动弹簧均固定在基座上。连接件将电磁弹簧、气动弹簧和负载连接起来从而保证环形磁体、活塞杆及负载具有相同的运动。

当承担载荷的隔振系统处于静平衡位置时，环形磁体与上下线圈绕组之间的距离相等，负载完全由气动弹簧承担。通过选择合适的线圈电流和气室气压，隔振系统能够在静平衡位置处获得准零刚度特性，降低系统的固有频率，进而提高低频隔振性能。

2 静力学分析

2.1 电磁力的计算

为了分析隔振系统的静力学特性，首先推导电磁弹簧电磁力的解析表达式。本研究采用细丝法[15]计算电磁力，通过对2个麦克斯韦环形电流之间的电磁力进行叠加得到通电线圈和环形磁体之间的电磁力。细丝法计算模型如图2所示。

图2（a）展示了底部通电线圈C和环形磁体M的简化模型及相关参数。通电线圈可以看作轴向和径向多个环形电流的叠加，而环形磁体等效于内壁和外壁都带有NHM个回路电流的通电螺线管，内壁和外壁上通电回路的电流方向相反，等效分割模型如图2（b）所示。图2（c）为选择的2个计算电磁力需要的麦克斯韦环形电流。由细丝法可知，等效螺线管A内壁和底部通电线圈C之间的电磁力FAC为

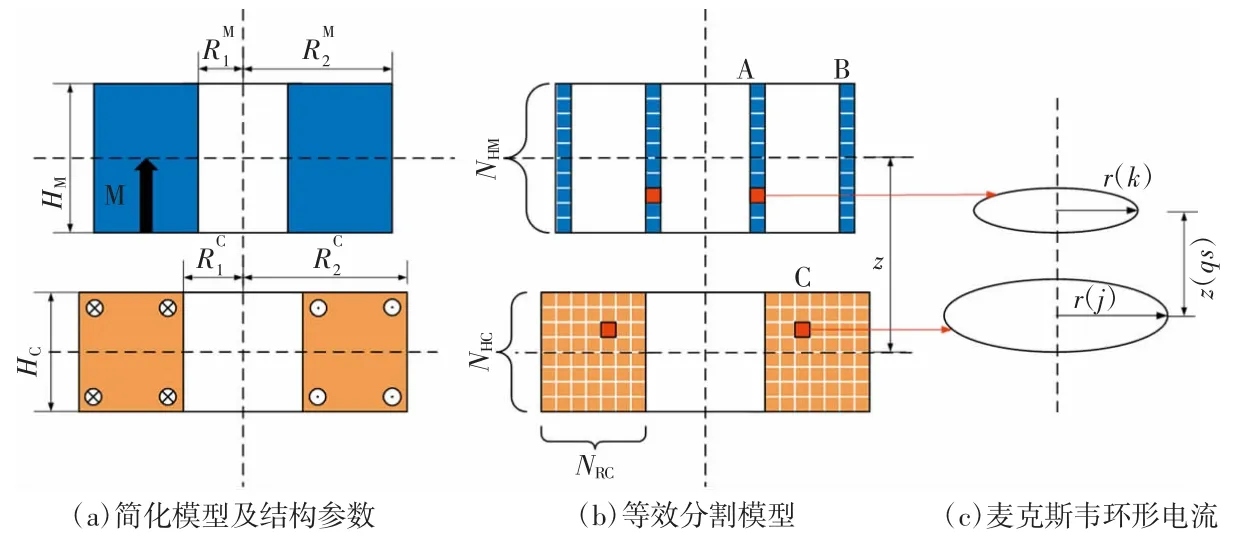
图2 细丝法计算模型

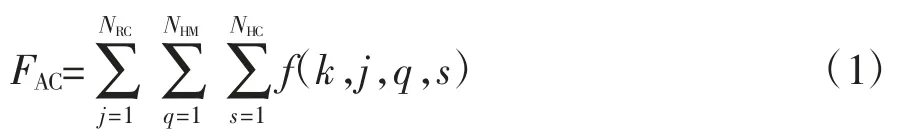
式中，f（k，j，q，s）为求得的2个通电细丝之间的力，计算公式如下：

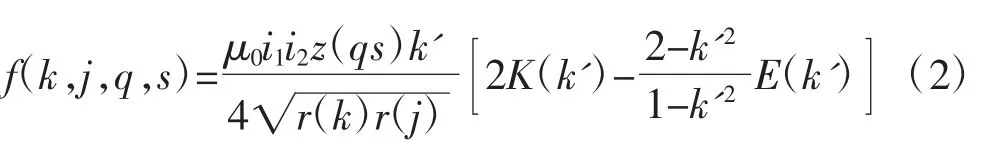
式中，μ0=4π×10-7H/m，为真空磁导率；K（k'）与E（k'）分别为第一类和第二类椭圆积分；i1与i2为螺线管和线圈每个环形细丝的电流，i1与i2由公式（3）计算得到：

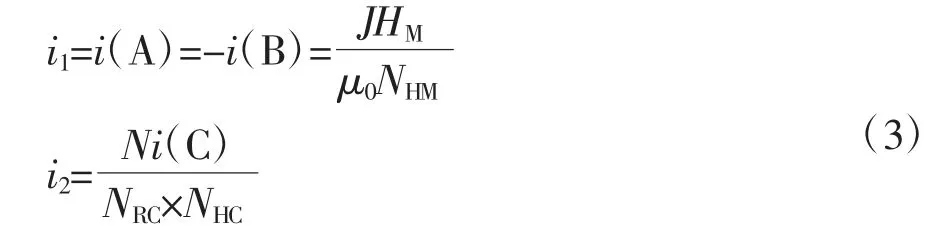
式中，J为环形磁体的磁化强度；N为线圈匝数；i（A）与i（B）为等效螺线管A和B的每个环形细丝的电流；i（C）为线圈电流。

公式（2）中其他参数计算公式如下：

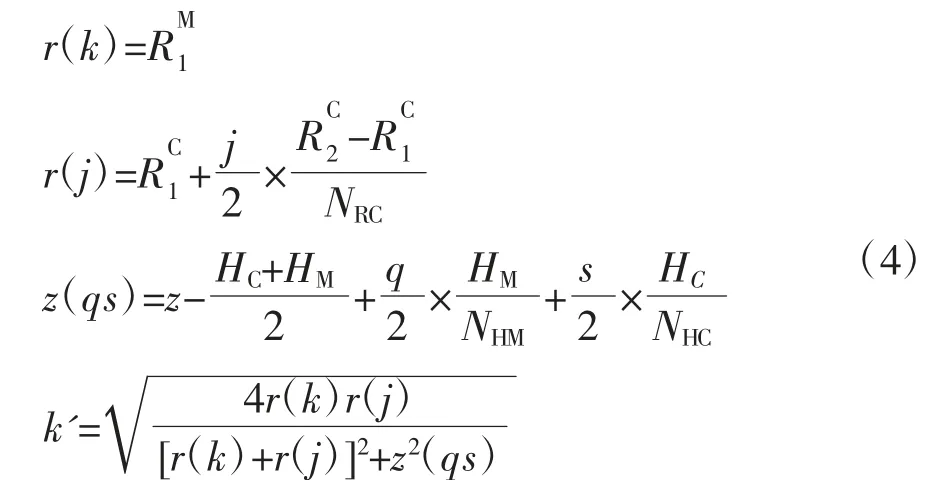
同样地，整个负刚度机构的电磁力FNSM为

式中，FAC、FAD、FBC、FBD分别为等效螺线管A、B与底部和顶部通电线圈C、D之间的电磁力。

电磁力与环形磁体位移及线圈电流的关系曲线如图3所示。由图3可知，电磁力曲线与三次方曲线近似，且上述电磁力的计算涉及到椭圆积分，较为复杂，因此采用三次方多项式对电磁力进行拟合，从而简化计算，拟合结果见公式（6）：

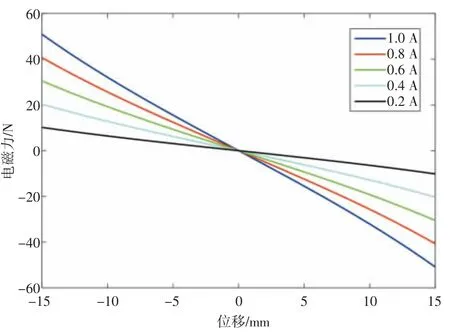
图3 电磁力与磁体位移及线圈电流的关系

式中，a与b分别为三次方项和线性项拟合参数；x为环形磁体位移；i为通入电磁弹簧的线圈电流。

2.2 气动弹簧回复力的计算

气动弹簧包含上下2个气室，通过压力差来支撑负载。气动弹簧回复力解析表达式的计算主要基于理想气体可逆多变方程：

式中，p为气体气压；V为气体体积；λ为气体多变指数，在绝热等熵过程中，λ一般取1.4；const为常数。

当活塞向下运动x时，气动弹簧的回复力Fp为

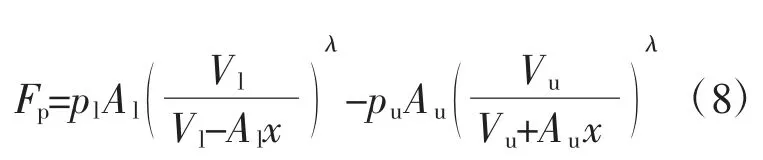
式中，pu、pl，Vu、Vl，Au、Al分别为上下气室气压、体积和截面积。

设上下气室初始高度为hu与hl，则

将公式（9）代入公式（8）化简得到气动弹簧的回复力Fp为

2.3 隔振系统的静态特性分析

将电磁弹簧和气动弹簧并联得到一种新型的隔振器，当隔振质量为m时，系统回复力F的表达式为

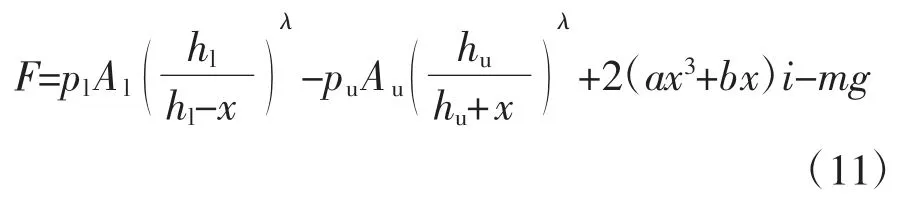
刚度K的表达式为

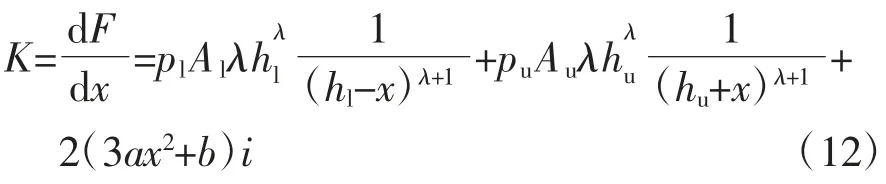
当隔振系统参数RC1=11.8 mm、RC2=49.2 mm、RM1=13 mm、RM2=40 mm、HC=36 mm、HM=32 mm、J=1.35 T、z=49 mm、NRC=55、NHC=50、NHM=80、hl=35 mm、hu=25 mm、Al=490.9 mm2、Au=412.3 mm2、pl=0.204 MPa、pu=0.124 MPa时，隔振系统在不同线圈电流下的回复力-位移曲线及刚度-位移曲线如图4所示。

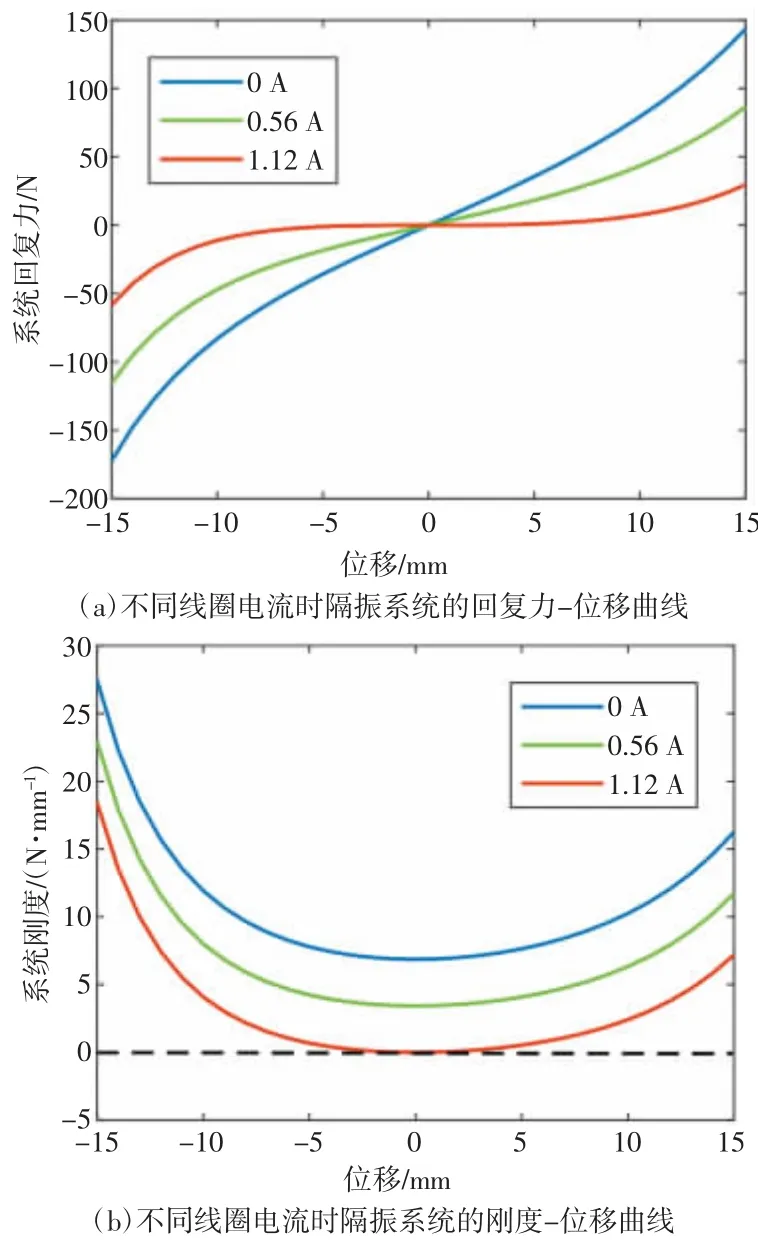
图4 隔振系统在不同线圈电流下的回复力-位移曲线及刚度-位移曲线

图4（a）展示了通入不同电流时隔振系统的回复力-位移曲线以及通入电流后整个隔振系统的回复力变化。可以看出随着通入电流的增大，隔振系统的回复力-位移曲线变得平缓。当通入电流为1.12 A时，回复力-位移曲线在静平衡位置附近小范围内趋于水平，此时回复力几乎保持不变。从图4（b）中可以看出，当通入电流为1.12 A时，系统刚度在静平衡位置附近趋近于零。因此在系统参数确定的情况下，选择合适的气室气压和线圈电流能够使隔振系统得到准零刚度特性。

2.4 回复力-位移关系近似

为了简化计算，对隔振系统回复力进行泰勒展开近似。将公式（11）在静平衡位置附近进行七阶泰勒展开近似，即

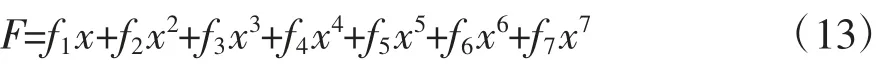
式中，f1、f2、f3、f4、f5、f6、f7为泰勒多项式系数，近似结果如图5所示。

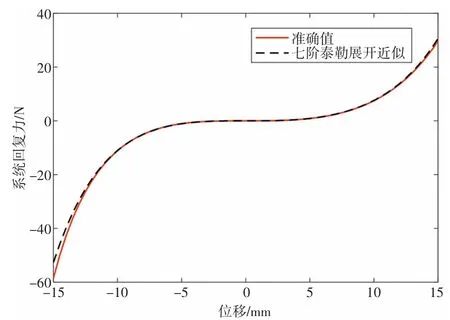
图5 隔振系统回复力-位移曲线与泰勒近似曲线

从图5可以看出，在静平衡位置附近15 mm范围内近似力与准确值误差较小，尤其在10 mm范围内几乎完全吻合，因此在进行动力学特性分析时回复力可以采用近似表达式从而简化计算。

3 动力学分析

3.1 谐波激励下的力传递率

由于环形磁体与活塞杆只在垂直方向上运动，因此隔振系统可以等效为垂直方向上的刚度为K、阻尼为c的单自由度系统，在进行隔振系统的动力学分析时，隔振系统的回复力由近似表达式（13）计算。设负载受到Fecos（ωt）（Fe为激励幅值，ω为激励频率，t为时间）的谐波激励时向下运动位移为x，根据牛顿定律和达朗贝尔原理可得隔振系统的无量纲动力学方程：

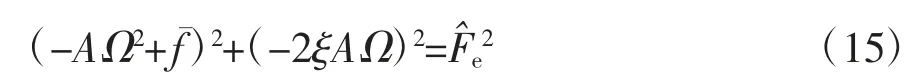
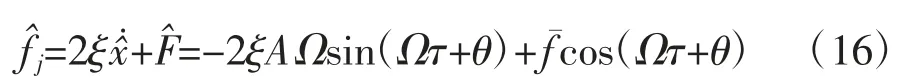
隔振系统力传递率Tf定义为传递到基座上的力的幅值与激励幅值的比值，采用分贝形式来表示，即

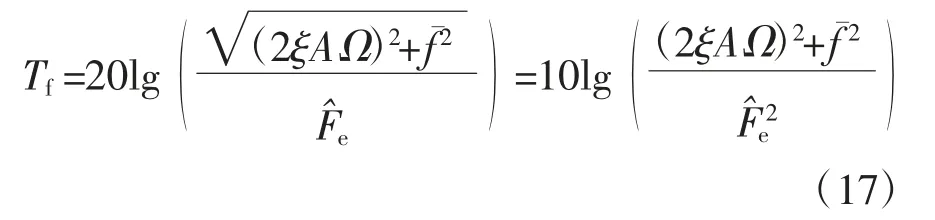
3.2 隔振性能

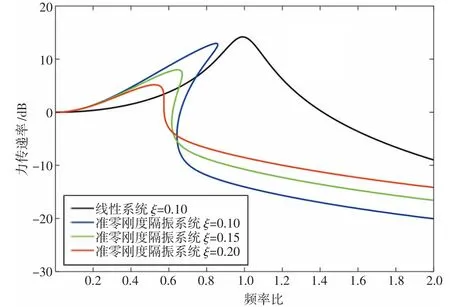
图6 不同阻尼比时准零刚度隔振系统及线性系统的力传递率

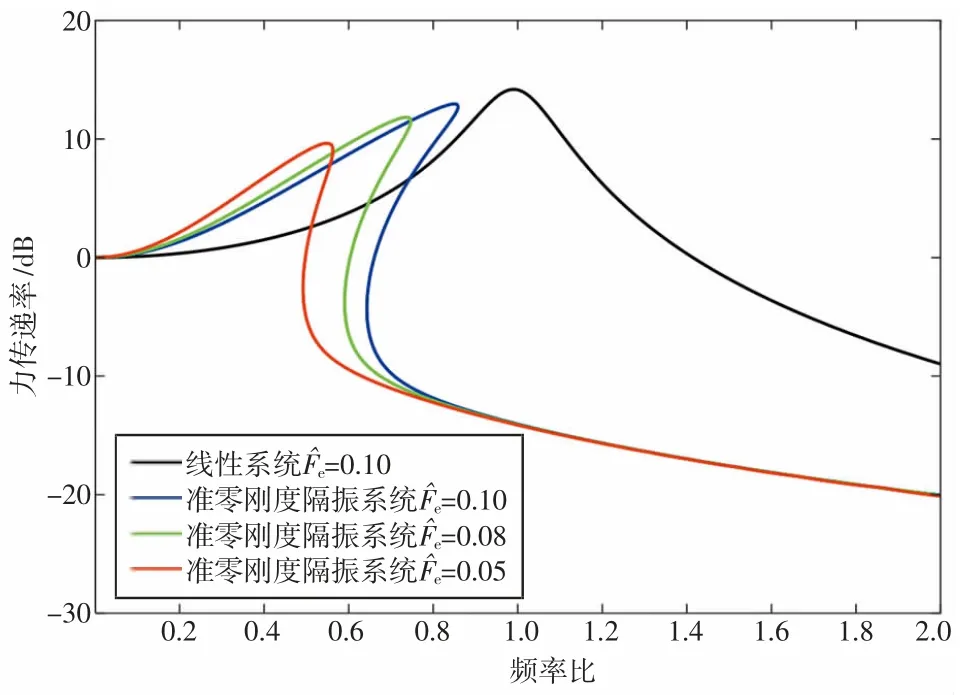
图7 不同激励幅值时准零刚度隔振系统及线性系统的力传递率

4 结语

针对传统的线性隔振系统存在低固有频率和高静态支撑能力的固有矛盾而难以降低救护车辆搭载的座椅与担架受到的低频振动干扰，本研究通过将提供负刚度的电磁弹簧和提供正刚度的气动弹簧并联设计了一种新型的准零刚度隔振器，并分析了隔振系统的静力学特性，得出系统的刚度解析模型和获得准零刚度特性的方法。同时建立了系统的动力学模型，得到隔振系统的力传递率并与线性隔振系统进行比较。力传递率结果表明准零刚度隔振器的传递率峰值和起始隔振频率均小于线性隔振系统，能够实现低频隔振的目标。较小的激励或较大的阻尼比都能够降低系统的起始隔振频率，扩宽隔振频带。因此设计的隔振器能够应用于车载担架或座椅上，进而降低低频振动干扰，提高伤员的乘卧舒适性。但提供负刚度的电磁弹簧的尺寸较大，应进一步研究在保持负刚度大小不变的前提下如何减小电磁弹簧尺寸。此外，由于正负刚度可调，可以进一步探究改变载荷下隔振系统保持准零刚度特性的可能性，从而扩大隔振器的适用范围。