永磁涡流联轴器模型结构合理性的试验验证
2021-09-23李延民朱永建
李延民,朱永建,胡 钡
(郑州大学机械工程学院,河南 郑州450001)
1 引言
永磁涡流联轴器是一项新近开发的新技术,可实现主、从动轴不接触达到转矩传递的目的,易于实现软启动、过载保护,同时极大的减小了整体结构的振动,有助于提高传动的可靠性,提高系统的使用寿命[1]。
国内对永磁联轴器的研究起步较晚,并且多偏向于理论仿真研究,而对实际的结构模型缺乏试验验证。本文简述永磁涡流联轴器的结构、工作原理以及理论分析[3-4],运用Ansoft[5]软件对模型结构进行有限元分析,最后通过试验台对模型进行试验验证,通过仿真数据与试验数据的对比分析,验证模型结构的合理性。同时对转速差进行试验[6-7],得出满足输出转矩时转速差的范围。
2 工作原理
永磁涡流联轴器由主动端和从动端构成,主动端包括导磁盘和铜盘为主,从动端包括导磁盘、铝盘、永磁体。永磁体成环形N、S极相互交错内嵌于铝盘体内。基本结构,如图1所示。

图1 永磁涡流联轴器的基本结构.Fig.1 Basic Structure of Permanent Magnet Eddy Current Coupling
工作原理:铜盘随着电机的启动而快速旋转,铜盘因切割的磁感线,在铜盘表面形成圆周分布的涡电流,涡电流会形成反感磁场,并且与永磁体产生的磁场相互作用实现转矩的传递。
3 转矩计算的数学模型
永磁联轴器的模型结构,如图2所示。其中,δ-气隙(mm),H-导磁铁厚度(mm),HC-铜盘厚度(mm),HW-永磁体厚度(mm),R1-永磁体外径(mm),R2-永磁体内径(mm)。

图2 永磁涡流联轴器一侧分析模型Fig.2 The Analysis Model of the Permanent Magnet Eddy-current Coupling
计算时记Ω-整个求解域为,Г1-模型的内外侧面,Г2-不同介质交界面,为Г3-导体盘沿从动转子半径方向的侧面,在Ω内求解磁矢位B:
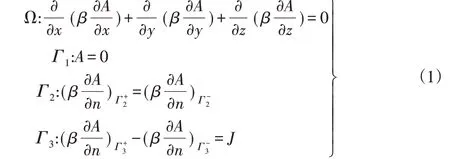
式中:β—磁阻率,n-Г2、Г3的法向量。μ0—空气磁导率,钕铁硼N35材料取β≈1/1.099μ0。由磁矢位A可得磁感应强度B:

根据式(2)求得场强B,从而得到永磁涡流联轴器的转矩为:

式中:V—气隙的体积(mm3);R1—导体盘的外半径(mm),R2—导体盘的内半径(mm)。
3 仿真模型的建立与研究
图3为仿真模型基本结构。设计的永磁涡流联轴器为对称结构,因此仿真时对单面结构进行有限元分析,当转矩达到一半时即可满足传递需求。

图3 永磁涡流联轴器仿真模型Fig.3 Simulation Model of Permanent Magnet Eddy-current Coupling
进行系列化参数研究时,仿真过程中设定的常参数,如表1所示:

表格1分析模型基本参数Tab 1 Analysis Model Basic Parameters
4 试验验证
4.1 试验装置
为永磁涡流联轴器的试验平台,为便于试验,样机采用的依旧是单面结构。试验时Y132三相异步电机为样机提供动力,CZ5磁粉制动器通过调节张力控制仪为样机提供负载。利用ZH07转矩转速传感器可测量转矩、转速。利用此试验平台达到以下试验的目的,如图4所示。

图4 永磁涡流联轴器的试验平台Fig.4 Test Platform of Permanent Magnet Eddy Current Coupling
(1)结构合理性的试验验证
(2)转速差的试验验证
4.2 结构合理性的试验
4.2.1 试验方案
试验前,为确保试验数据的准确性,需检验传感器的零点是否发生漂移,否则要进行归零设置。试验开始时,通过磁粉制动器张力控制仪调节直流大小,进行负载的调控,使得永磁涡流联轴器负载端达到所需转速。通过转矩转速传感器记录不同时刻对应的转矩值。为了更加直观对比分析仿真与试验数据的准确性,应用origin软件对二者进行处理,如图5所示。

图5 结构合理性仿真与试验结果对比Fig.5 Comparison of Structural Rationality Simulation and Experimental Results
如图所示,两条曲线基本吻合,试验值和仿真值具有很好的一致性,表明设计的结构能够达到传递转矩的要求。但是从图中可看出试验和仿真存在一定的误差,两者之间的最大误差5.97%,两条曲线没有完全拟合的主要原因是试验台运转时存在机械摩擦,同时在转动时铜盘上的涡流会产生热损耗。其次气隙调节存在一定误差,永磁涡流联轴器之间气隙是手动调节,很难精确保持3mm,因此会对转矩的测量产生一定影响。
4.3 转速差的试验验证
4.3.1 试验方案
转速差直接影响着传递转矩的效率。试验开始时,通过张力控制仪调节负载,依次增大转速差。通过转矩转速传感器记录不同转速差对应的转矩,与相对应的仿真数据进行对比分析。通过转矩转速传感器记录不同转速差对应的转矩,与相对应的仿真数据进行对比分析,如图6所示。
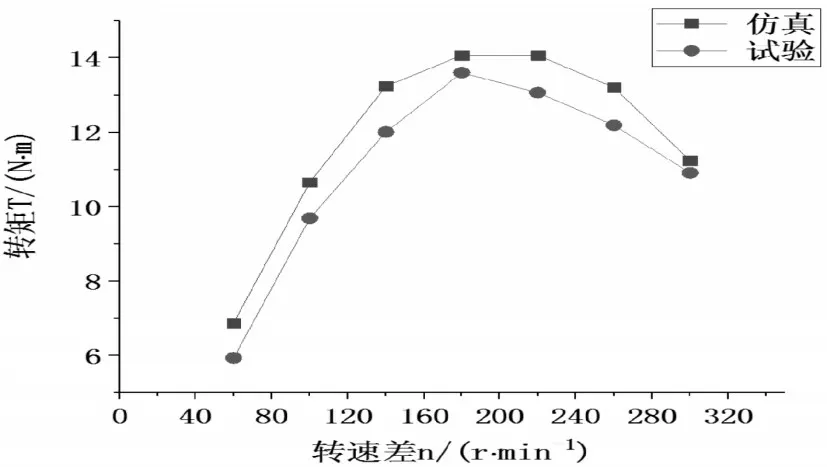
图6 转速差仿真与试验对比分析Fig.6 Comparison and Simulation of Speed Difference Simulation and Test
由图可知,两条曲线有相同的变化趋势,均随转速差的增加,转矩先增大后减小,先增大后减小。这是因为在转速差增大时,输出的功率增大,转矩增大,直到输出功率达到峰值,转矩不再增大。当转速差持续增加,在铜盘上产生的感应电流增大,铜盘上的功率损失增大,故而导致输出转矩减小由图可知。在满足输出转矩的要求,转速差可在140-180rpm选取。
虽然转速差的仿真值与试验值两条曲线变化趋势基本吻合,但还是存在误差。导致误差的原因是机械摩擦、涡流损耗、操作误差。操作误差主要是控制仪的调节误差,手动调节电流大小从而调节负载轴的转速,因此在调节过程有一定的误差。
5 结论
本文通过对与7.5KW、4极电机相匹配的永磁涡流联轴器的样机进行仿真分析与试验,验证样机可达到输出转矩的要求,验证模型结构的合理性。同时通过转速差的试验得出,当转速差可在140-180rpm时,均可满足转矩传递的需求。
