减振垫刚度变化对U型梁桥系统振动及结构噪声的影响研究
2021-09-23孔晓钰
胡 传,陈 诚,吴 雪,孔晓钰
(1. 成都地铁运营有限公司,成都 610058;2. 高速铁路线路工程教育部重点实验室,成都 610031)
U型梁桥因其造型美观、隔声效果好、断面空间利用率高等优势逐渐成为城市轨道交通高架结构的常见桥型[1]。目前,国内外的研究主要集中在钢桥、箱型梁桥的桥梁振动噪声预测与现场实测上。Janssens和Thompson[2]介绍了一种可以计算钢结构桥的模型,并发现由钢结构桥产生的噪声水平要比普通混凝土桥高大概10 dB,且钢结构桥的噪声不仅是由其本身产生的,而且上部轨道系统贡献量也较大。Walker等[3]通过有限元方法计算了混凝土桥和钢桥轮轨噪声及结构噪声水平,通过将计算结果与实测结果对比得到了验证,还测试了不同降噪措施的效果,为减振降噪措施的研究提供了参考。李宝银[4]曾基于有限元与边界元联合的方法计算了高速铁路典型32 m简支箱梁的结构振动与声辐射特性,最终得到32 m简支箱梁的振动与噪声传播、衰减规律及两者间的关系。韩江龙等[5-7]采用模态叠加法计算列车经过城市轨道交通槽型梁、箱梁时的振动响应,并采用有限元与边界元相结合的方法计算桥梁的结构噪声。尹航[8]分析计算了U型梁桥在列车作用下的振动与低频结构噪声辐射情况。张鹤[9]自编程序给出桥梁噪声的数值解、声压的空间分布及其随时间的变化规律。邓子铭等[10]建立列车和桥梁有限元模型,研究了不同车速下的车桥耦合系统空间响应。关于高架桥梁振动噪声研究多数是关注桥梁本身的响应及其影响因素,对上部轨道结构参数对桥梁结构响应的影响关注较少,随着U型梁桥的广泛运用,有必要在这些研究的基础上加强对U型梁桥的研究。
U型梁的梁体较薄,质量和刚度都较小,这种特性导致桥梁结构辐射噪声非常明显。另外,列车高速通过时会增加安装在桥梁上部的声屏障结构振动,使声屏障成为新的结构噪声源,降低整体降噪效果,影响到高架周边居民的生活乃至身心健康[11],因此需要对U型梁桥系统的振动和噪声进行预测。
实际工程中,U型梁桥结构常采用隔离式减振垫浮置板以达到减振降噪的目的。合理的减振垫刚度不仅能保证列车行车安全,还能有效地减缓轮轨相互作用,保持良好的轨道几何形位,从而减少养护维修的工作量[12]。因此,研究减振垫刚度对U型梁桥系统振动及结构噪声的影响意义重大。
针对减振垫刚度参数影响及敏感性问题,国内学者曾做过一些研究。余庆[13]建立了隔离式减振垫的有限元模型,研究其固有频率和动力学响应,并分析了它的减振性能;于鹏等[14]建立了列车-板式减振轨道-轨道下部基础模型,对不同减振垫刚度下的轨道结构的减振性能进行分析。杨文茂[15]建立车辆-轨道-隧道耦合动力学模型,研究了减振垫浮置板的动力学特性,结果表明,减振垫刚度宜取0.01~0.02 N/mm3。但目前这些研究都未涉及减振垫刚度对U型梁桥系统结构的影响,减振垫刚度对车辆-轨道-U型梁桥耦合系统的影响规律还不明确。鉴于此,以隔离式减振垫为研究对象,基于刚柔耦合理论,采用有限元法和多体动力学建立车辆-轨道-U型梁桥耦合动力学模型,研究减振刚度变化对U型梁桥系统振动及结构噪声时域的影响规律,为高架段的轨道设计提供参考。
1 刚柔耦合模型
基于多体动力学和有限元方法,建立车辆-轨道-桥梁刚柔耦合动力学模型,并在多体动力学软件中实现联合仿真。其中车辆考虑为多刚体模型,轨道结构和U型梁桥考虑为柔性体模型,两个子模型通过非线性轮轨接触耦合。
1.1 车辆刚体模型
车辆动力学模型如图1所示,其中参数的含义及原始数值见表1。
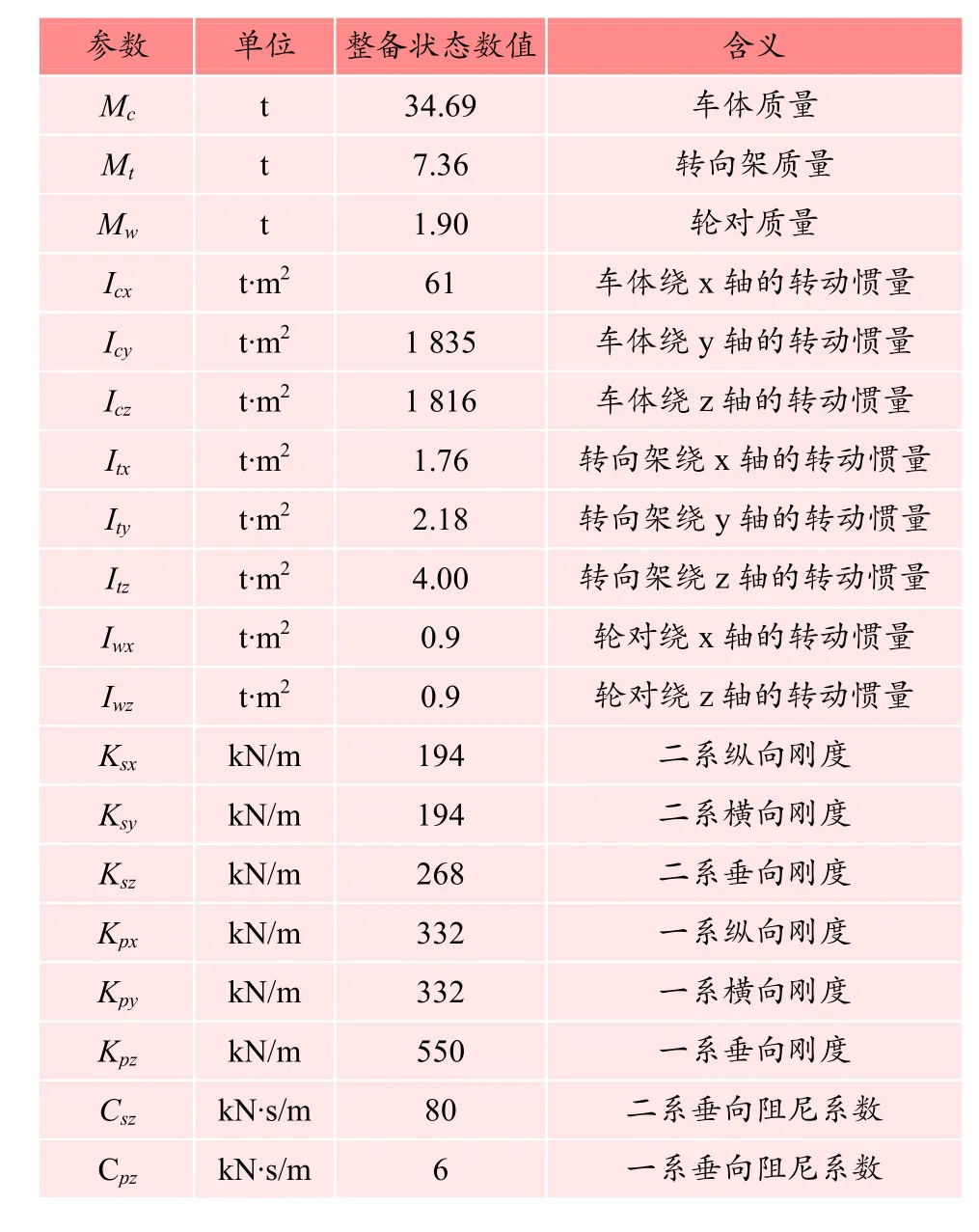
表1 车辆模型的参数含义以及原始数值Table 1 Parameters of the vehicle model and the original values
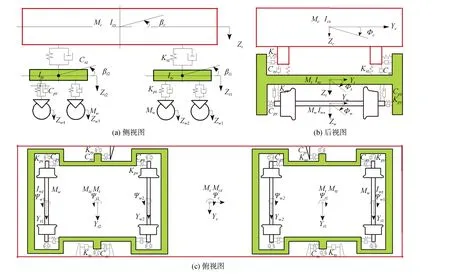
图1 车辆动力学模型 Figure 1 Vehicle dynamics model
1.2 柔性体系统模型
柔性体模型包含轨道结构和U型梁桥两个部分。钢轨考虑垂向、横向和扭转三方向自由度,用离散点支承基础上的Timoshenko梁[16-17]模拟;钢轨和轨道板之间通过扣件连接,垂向等效刚度和横向等效刚度用Kz、Ks表示,垂向等效阻尼和横向等效阻尼用Cz、Cs表示;轨道板与道床之间通过减振垫连接,采用线性弹簧单元模拟,垂向等效刚度和阻尼用Kfz和Cfz表示,横向等效刚度和阻尼用Kfy和Cfy表示,通常减振措施会根据轨道减振结构中轨道板与道床的连接方式换算为等刚度的弹簧进行设置。轨道板与混凝土基底之间设置隔离式减振垫进行连接,减振垫刚度一般用面刚度表示[15]。本研究采用满铺减振垫的方式,因此面刚度与减振垫面积相乘得到的总刚度与弹簧个数比即为单个线弹簧的刚度值。轨道板之间设置剪力铰进行连接;混凝土基底与桥梁之间采用Bushing力元进行连接, 垂向等效刚度和阻尼表示为Kbz和Cbz,横向等效刚度表示为Kby和Cby表示;U型梁桥使用实体模型,为消除边界效应,桥梁计算长度取3跨,两端通过支座约束,如图 2所示。上述结构动力学参数和几何参数见表2。计算分析中的不平顺采用的是德国高干扰谱。
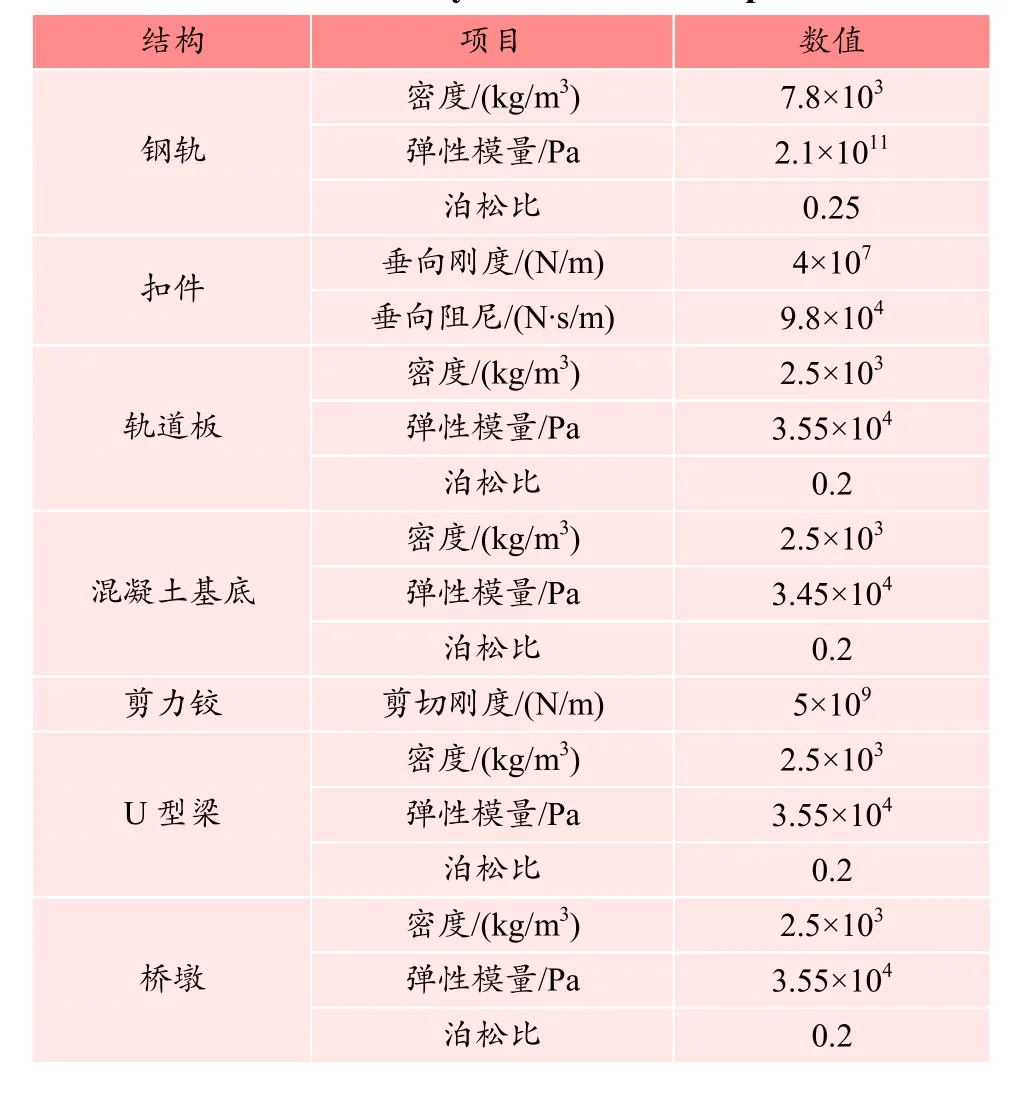
表2 柔性体结构模型参数Table 2 Flexible body structure model parameters

图2 柔性体结构模型 Figure 2 Flexible body structure model
1.3 轮轨接触
轮轨接触用于连接车辆系统和轨道结构,是模型中重要的组成部分。已有研究表明[18],轮轨的垂向振动和横向振动之间存在弱耦合关系,且这种弱耦合关系是单向的,即垂向振动可看作是独立,而横向振动会受到垂向振动的影响。目前,国内外计算理论和仿真模型中,通常将赫兹接触理论用于轮轨接触分析,其理论计算如公式(1)所示。
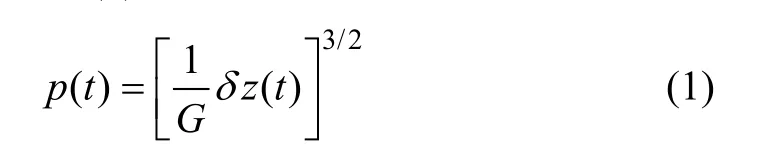
式中,G为轮轨接触常数,单位为m/N2/3;δz(t)为轮轨间弹性压缩量,单位为m。本研究基于多体动力学软件仿真,垂向轮轨力计算基于赫兹非线性弹性接触理论,横向轮轨力建立在赫兹接触理论基础上,并使用Kaller滚动接触的非线性简化理论FASTSIM算法[19]。
2 模型验证
将建立的车辆-轨道-桥梁刚柔耦合模型的计算结果与以往文献做对比以验证模型的有效性。目前,大多数关于U型梁桥的仿真研究都是车线耦合,故分为两步进行验证,先验证车辆-轨道系统,在此基础上验证U型梁桥计算结果的正确性。
2.1 轨道结构模型验证
按照参考文献[20]中的模型参数进行设置,车辆模型采用CRH2型动车,车速为300 km/h,输入德国低干扰谱不平顺,钢轨和轨道板的跨中垂向振动加速度和位移的时域变化如图3所示。轨道板振动响应如图4所示。
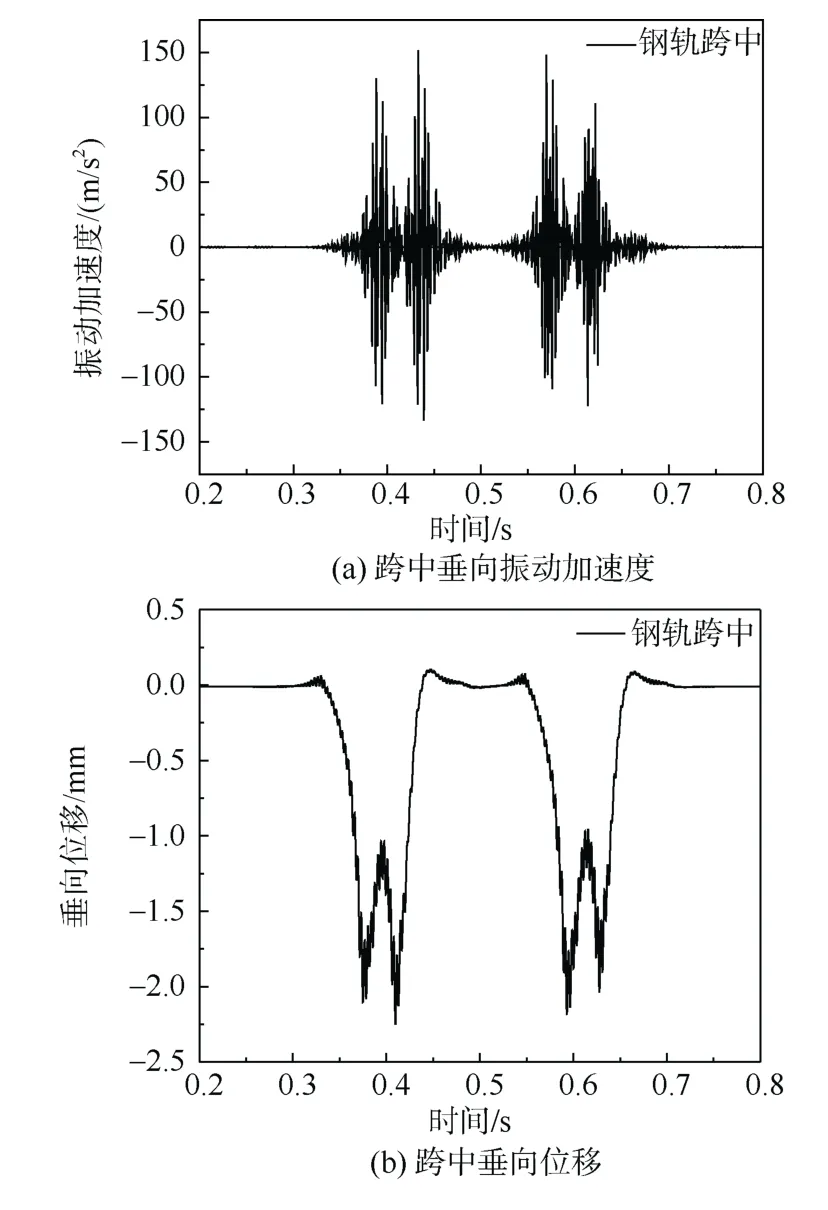
图3 钢轨动力响应 Figure 3 Rail dynamic response
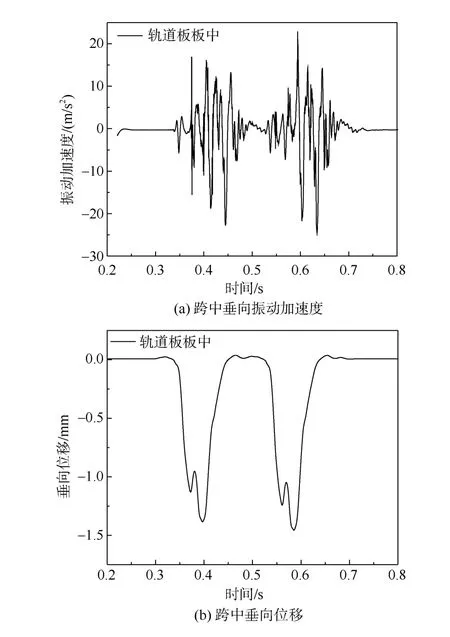
图4 轨道板振动响应 Figure 4 Vibration response of track plate
将基于本模型计算所得的结果(即图3和图4)与文献[20]对应的结果进行对比,发现两者的波形和量值都有较好的吻合度,考虑到本模型中的部分轨道结构参数无法做到与参考文献中的模型完全一致,且计算方法也不相同,故计算结果略有差异,但其反映出的轨道结构动力特性较为一致,故建立的轨道结构模型具有良好的计算精度。
2.2 U型梁桥结构模型验证
参照参考文献[21]中的参数进行设置,车辆模型采用地铁A型车,车速为100 km/h,输入德国低干扰谱不平顺,波长范围是1~200 m,U型梁桥的跨中垂向振动加速度和位移的时域变化如图 5所示。与文献[21]中对应的结果进行对比后发现,两者在波形以及量值上都具有较高的吻合度,验证了U型梁桥结构模型的有效性。
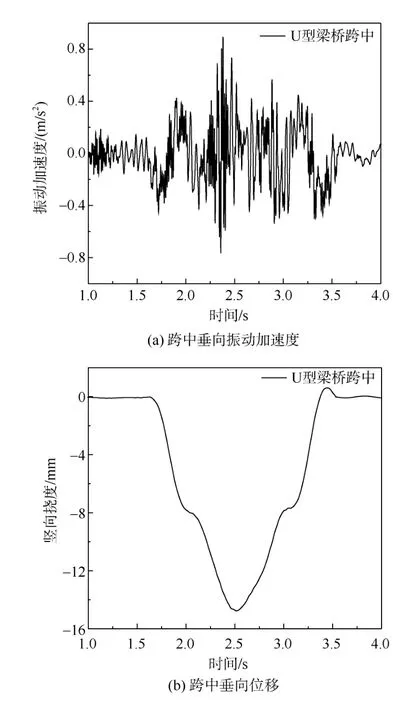
图5 U型梁桥振动响应 Figure 5 Vibration response of U-beam bridge
3 计算结果与分析
3.1 系统振动响应
钢轨及轨道板跨中垂向加速度和位移的时域变化如图6和图7所示。
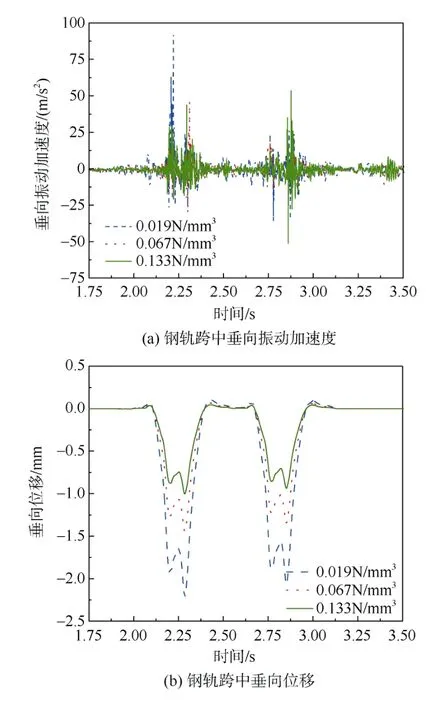
图6 钢轨振动响应 Figure 6 Rail vibration response
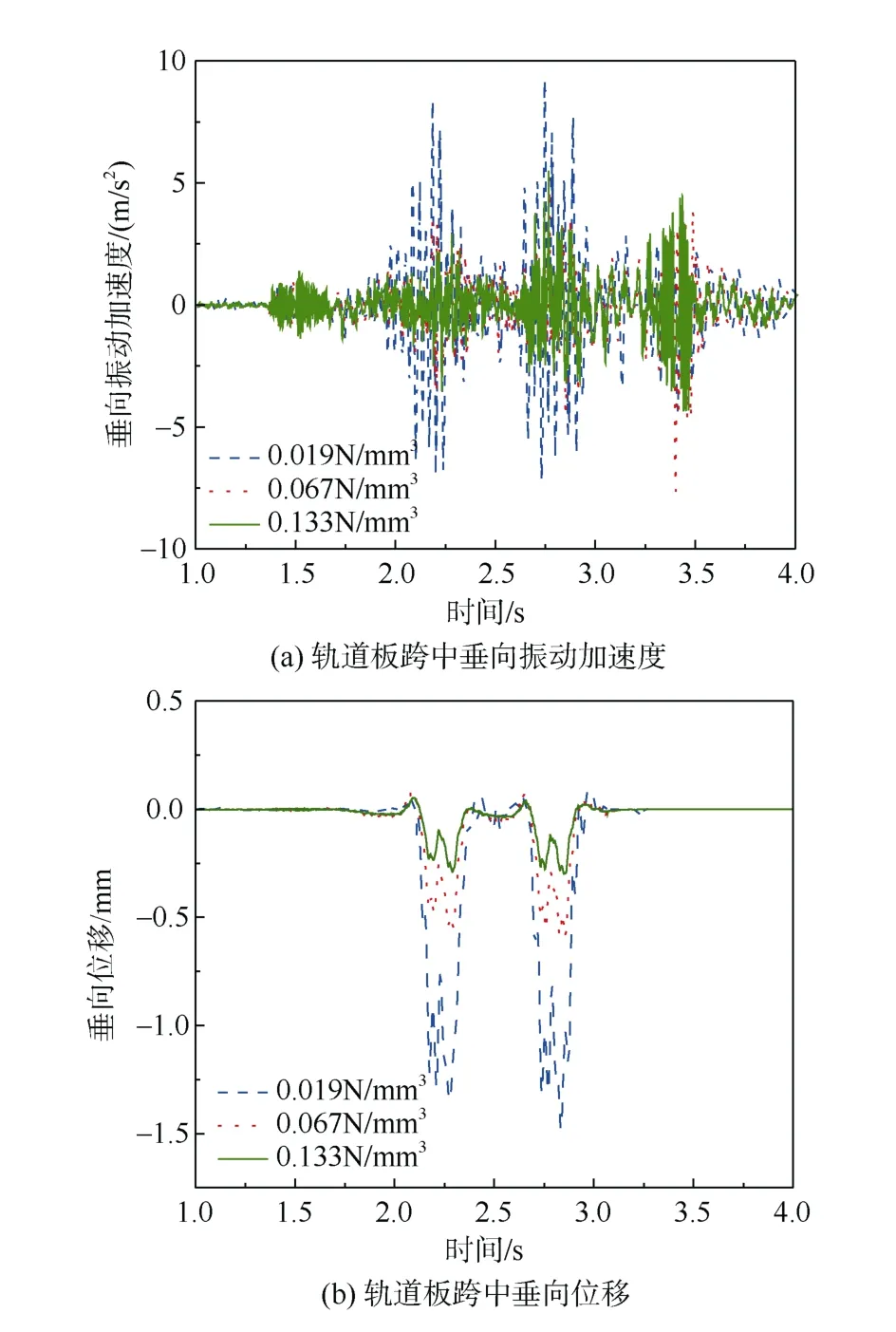
图7 轨道板振动响应 Figure 7 Rail vibration response
由图6和图7可知,改变减振垫的刚度对钢轨、轨道板跨中垂向加速度和垂向位移的分布规律影响较小,只改变幅值的大小。为了直观反映减振垫刚度对轨道系统以及桥梁的影响,提取钢轨跨中以及轨道板跨中垂向加速度和位移幅值以及有效值进行简要分析,如图8、图9所示。其中,S1、S2、S3分别代表减振垫垂向刚度为0.019、0.067、0.133 N/mm3时的情况。
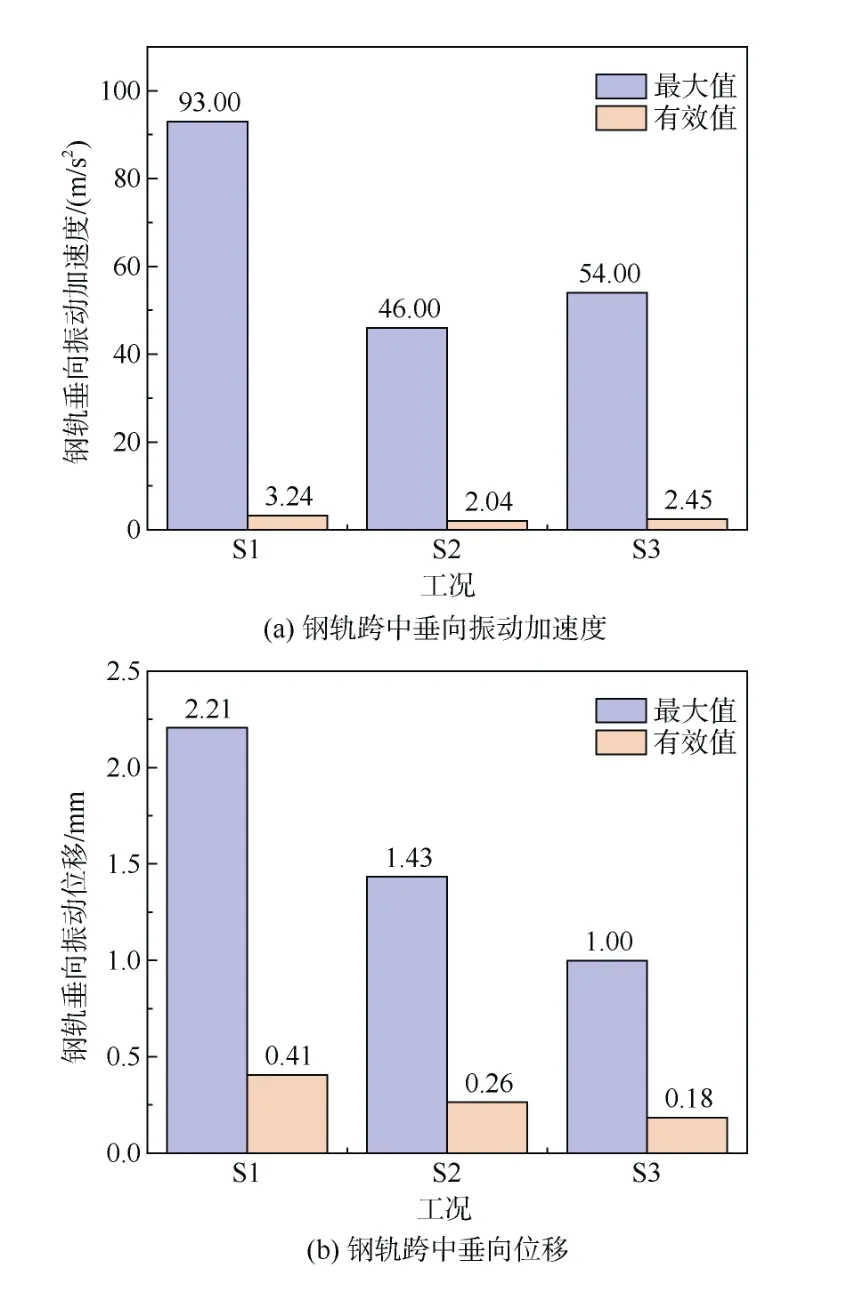
图8 钢轨振动响应 Figure 8 Rail vibration response
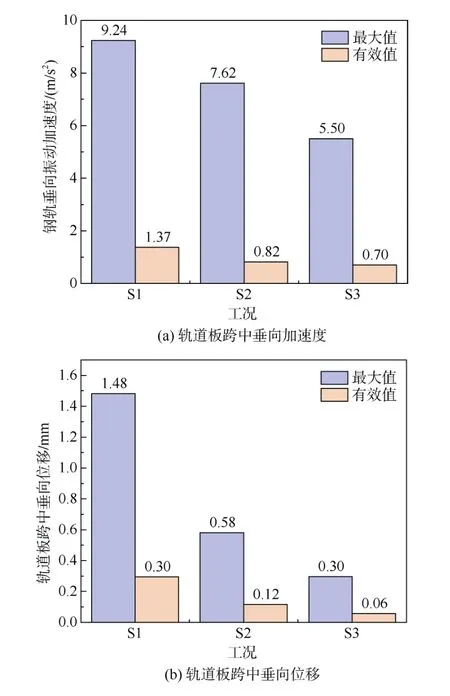
图9 轨道板振动响应 Figure 9 Vibration response of track plate
由图8(a)可以看出,减振垫的刚度并非越大越好,刚度过大时,钢轨的振动响应反而比刚度较小时更剧烈;由图8(b)可知,钢轨跨中垂向振动位移均随着减振垫刚度的增大而减小,三种隔振垫刚度的情况下钢轨跨垂向最大位移依次减小36.4%和35.7%,有效值依次减小36.6%和30.7%;另一方面,钢轨位移变化量与减振垫刚度变化量对比可知,钢轨位移下降的幅度随着刚度的增加逐渐变缓。
由图9可知,减振垫刚度的变化会直接影响到轨道结构的形变,轨道板的垂向振动加速度和位移随减振垫垂向刚度增大而减小。从工况一到工况三,轨道 板跨中垂向振动加速度幅值依次减小1.62 m/s2和2.12 m/s2,有效值依次减小0.55 m/s2和0.12 m/s2;轨道板跨中垂向位移幅值依次减小0.9 mm和0.28 mm,有效值依次减小0.18 mm和0.06 mm。由此可以看出,减振垫刚度增加会放缓垂向位移减小的速度,轨道板的变形随着减振垫垂向刚度的增加逐渐趋于平稳。
U型桥梁振动响应如图10所示,当减振垫垂向刚度从0.019 N/mm3增大到0.133 N/mm3时,U型梁桥跨中垂向振动加速度幅值依次增加69.6%和4.7%,有效值依次增加67.3%和11.3%,总体呈增大趋势,但后期趋于平稳。桥梁的跨中垂向位移则基本保持不变,这是因为减振垫刚度远远小于桥梁结构的整体等效刚度,结合前面的计算结果可知,隔振垫越软,桥梁跨中垂向加速度越小,钢轨和轨道板跨中垂向加速度越大,这是由于减振垫刚度越小,减振垫越软,反弹到上部轨道结构的能量就越多,传递至桥梁结构的能量就越少。因此,适当减小隔离式减振垫的垂向刚度可以有效地达到减振的目的。
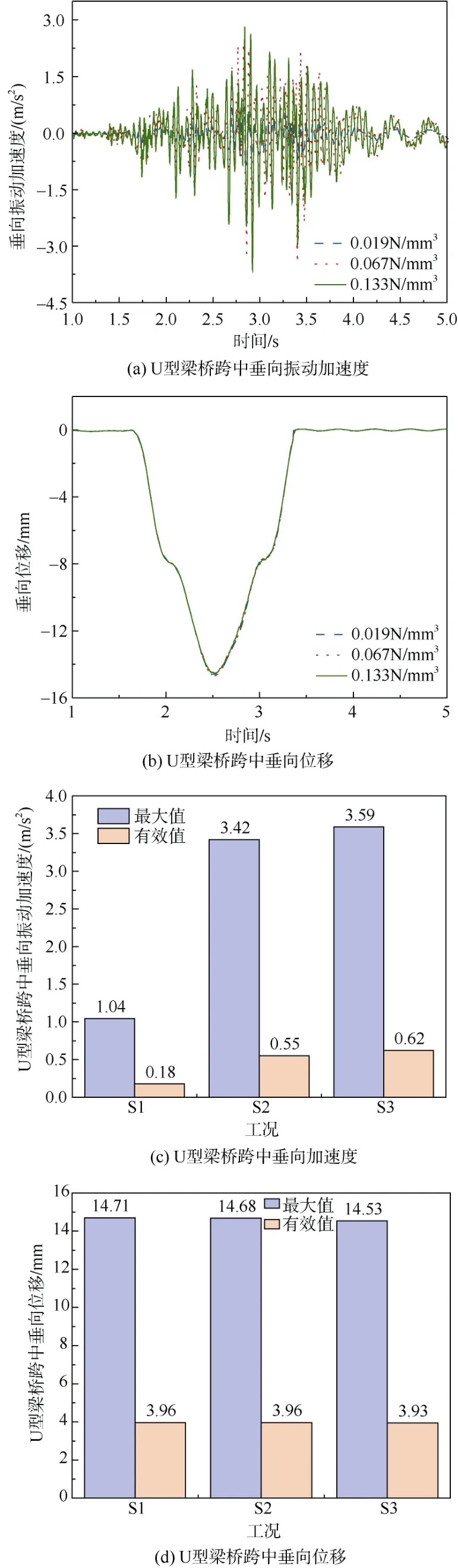
图10 U型梁桥振动响应 Figure 10 Vibration response of U-beam bridge
3.2 桥梁结构二次噪声
将系统仿真得到的U型梁桥表面的法向振动响应作为边界条件输出到comsol multiphysics软件的压力声学物理场模块进行桥梁结构二次噪声的计算,计算出的桥梁结构噪声时不包括轮轨噪声。噪声预测点的位置为横向距离外轨中心线7.5 m,垂向高出轨面1.5 m。评价指标上,考虑到A计权声压级在度量低频成分为主的噪声时,会产生误差,无法真实地反映人们对于噪声的感受[22],且研究表明桥梁结构二次噪声主要以低频为主[23],因此,为了真实反映列车通过时桥梁结构二次噪声频谱特性,采用线性计权进行分析。对比分析隔振垫垂向刚度分别为0.019、0.067、0.133 N/mm3时场点处的线性总计权,并进行频谱分析,结果如表3以及图11所示。
由表3和图11可知,隔离式减振垫刚度从0.019 N/mm3增至0.067 N/mm3和0.133 N/mm3时,线性总声级从91 dB增至95 dB和96 dB,随着刚度增大增速变缓。由频谱分析可知,桥梁结构噪声主要集中在12.5~80 Hz的低频部分,且普遍都在63 Hz处存在最大幅值,该峰值与桥梁结构固有频率有关[24];当减振垫垂向刚度为0.019 N/mm3时,桥梁结构噪声在12.5 Hz和50 Hz处出现明显峰值,12.5 Hz处峰值最大;而当垂向刚度分别为0.067 N/mm3和0.133 N/mm3时, 两者频谱曲线大致相同,都在20 Hz和63 Hz处存在峰值,但主频为63 Hz。另一方面,在40~200 Hz频率范围内,线性声压级随着刚度增大亦呈增大趋势,其在80 Hz处最为明显,而小于40 Hz范围内,线性声压级在12.5~16 Hz和25~31.5 Hz处出现明显变化;12.5~16 Hz范围内的噪声,在减振垫垂向刚度为0.019 N/mm3时明显大于另外两种工况,而在刚度处当减振垫刚度为0.067 N/mm3时,25~31.5 Hz处的线性声压级明显小于另外两种工况,而另外两种工况在此频率处的线性声压级几乎相等,这说明隔振垫刚度设置太小或者太大,会放大低频区的结构噪声,合理设置隔离式减振垫的垂向刚度大小有利于更好地实现减振降噪的目的。

表3 U型梁桥结构二次噪声线性总声级Table 3 U-shaped beam bridge structure secondary noise linear total sound level
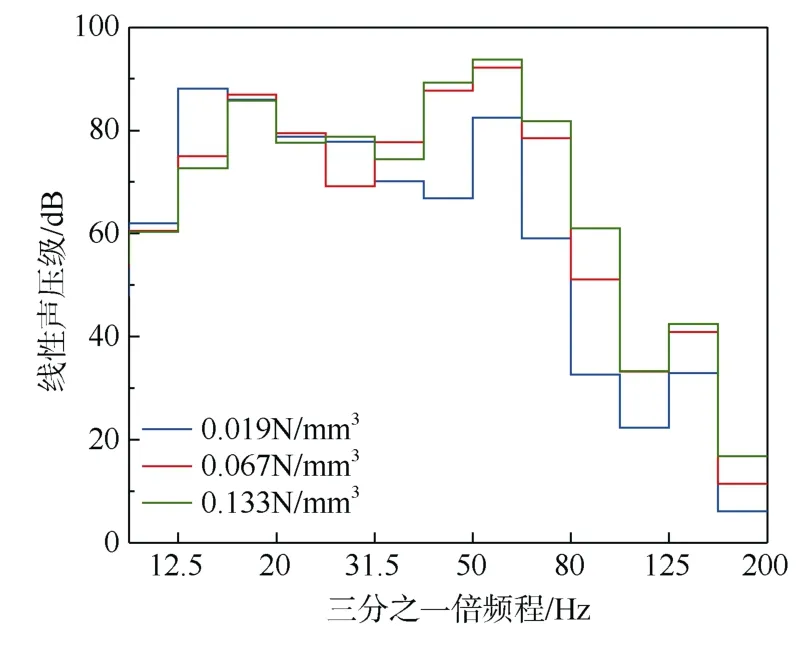
图11 场点桥梁结构噪声频谱 Figure 11 Noise spectrum of bridge structure at site point
4 结论
以设置了隔离式减振垫浮置板的U型梁桥区段作为研究对象,为了研究减振垫刚度变化对桥梁系统振动及结构噪声的影响,基于刚柔耦合理论,建立了动态车辆-轨道-桥梁耦合模型,并基于该模型研究了不同减振垫刚度下的桥梁系统振动响应和结构噪声,得到如下结论。
1)将建立的车辆-轨道-桥梁刚柔耦合模型的计算结果与以往文献进行对比发现,轨道结构振动响应和U型梁桥结构振动响应在时域具有较高的吻合度,验证了数值预测模型的有效性。
2)随着隔离式减振垫垂向刚度的增大,钢轨和轨道板的振动响应都出现不同程度的减小,但桥梁结构的振动响应被放大,可能导致过大的环境振动以及结构二次噪声。这是因为隔振垫刚度越硬,反射到上部轨道结构的振动能量越少,便有更多的能量传递到桥梁结构。
3)随着隔离式减振垫垂向刚度的增大,轨道结构和U型桥梁的振动幅值先是产生明显变化,随后逐渐趋于平缓。
4)隔离式减振垫垂向刚度增加会增大桥梁结构二次噪声,所以应该选取较小的隔振垫刚度,以达到抑制U型梁桥结构二次噪声的目的,但过小的垂向刚度可能会放大40 Hz以内低频区域的结构噪声,在实际应用时需要引起注意。
5)综合U型梁桥系统振动及结构噪声的计算结果,考虑到工程成本,用于高架结构的隔离式减振垫垂向刚度宜取0.067 N/mm3。
在进行桥梁结构二次噪声计算时仅计算了桥梁结构噪声,未考虑轨道板等部件振动产生的辐射噪声,计算结果与现场测试结果有出入,接下来的研究中需要改进桥梁结构噪声预测的方法,系统考虑系统各部件的振动情况,以得到更为完善的桥梁结构噪声预测模型来满足解决实际应用的需要。
