双有源全桥双向直流变换器的电路平均法建模
2021-09-23孙娟
孙 娟
(上海杰瑞兆新信息科技有限公司,江苏 连云港 222000)
0 引 言
为解决能源危机和环境污染问题,可再生能源联合发电系统已经成为当下的研究热点[1,2]。由于可再生能源发电存在间歇性问题,需要在系统中加入储能装置对能量进行调节,且能量是双向流动的,因此需要在系统中加入双向直流变换器进行能量调节[3]。
常用的隔离型双向直流变换器包括双向正激、双向反激、双向推挽、双向半桥以及双有源全桥双向直流变换器等[4]。其中,双有源全桥双向直流变换器结构简单对称,易实现软开关,电压电流应力相对较小,广泛应用于大功率场合[5]。通过改变其原边和副边全桥结构之间的移相角,即可方便控制能量传输的大小和方向。
为了保证双有源全桥双向直流变换器工作的稳定性,首先需要获得其小信号模型,并以此为基础设计性能优异的调节器参数。然而,由于开关器件的非线性,难以直接运用线性系统理论进行建模。目前,针对直流变换器的建模,应用最广泛的方法是状态空间平均法[6]。但该方法适用的前提是需要满足两个假设。一是低频假设,即扰动信号的频率需要远低于开关频率,此时可以忽略变换器的自然采样特性所导致的边带效应与混叠效应,从而简化模型。二是小纹波假设,即变换器状态变量中的开关纹波需要远低于其直流量,从而可以为变换器的小信号量提供恒定的直流工作点。然而,在双有源全桥双向直流变换器中,能量传输电感的电流不含直流量,其开关纹波远大于直流量,不满足小纹波假设,因此状态空间平均法并不适用。
针对双有源全桥双向直流变换器,一种可行的建模方法是离散建模法[7,8]。离散建模法是通过精确求解变换器的状态方程,得到变换器中变量在相邻两个开关周期同一采样时刻点的关系,再通过线性化得到小信号离散模型。因此相比于平均法,其准确性更高,适用范围更广。然而,由于双有源全桥双向直流变换器的状态方程是分段线性的,存在多组状态方程,因此大大增加了精确求解的难度。此外,离散建模所得的结果是z域模型,也并不适合工程运用。
基于以上问题,本文拟采用电路平均法进行双有源全桥双向直流变换器的建模[9]。电路平均法是将变换器中的非线性开关网络提取出来,仅对该网络的输入和输出变量进行平均化处理,而无需考虑开关网络中每个开关器件的行为特性,该方法不需要变换器满足小纹波假设,因此比状态空间平均法具有更大的应用范围。
本文首先回顾了双有源全桥双向直流变换器的工作原理,利用电路平均法对其进行了建模,得到移相角到输出电压的传递函数,并利用SIMPLIS软件对模型进行了验证。其次利用该模型,本文给出了调节器设计过程。最后在实验室搭建了一台6 kW的双有源全桥双向直流变换器原理样机,验证了理论分析的正确性。
1 双有源全桥双向直流变换器的工作原理
图1给出了双有源全桥双向直流变换器的电路拓扑,它由原副边两个全桥拓扑结构、一个能量传输电感以及一个高频变压器组成[10]。

图1 双有源全桥双向直流变换器的电路拓扑
双有源全桥双向直流变换器的常用控制方式为移相控制[11]。在该控制方式中,桥臂中点电压UAB和UCD的均为满占空比,通过控制这两个电压之间的移相角φ来控制电感电流,以实现功率的传递。移相控制方式的工作波形如图2所示。从上到下依次是原边桥臂中点电压UAB,折算到原边的副边桥臂中点电压U'CD,电感上的压降UL,电感电流IL,原边输入电压流I1,副边输出侧电流I2。图中,Ts为开关周期,K为变压器原副边的匝比。
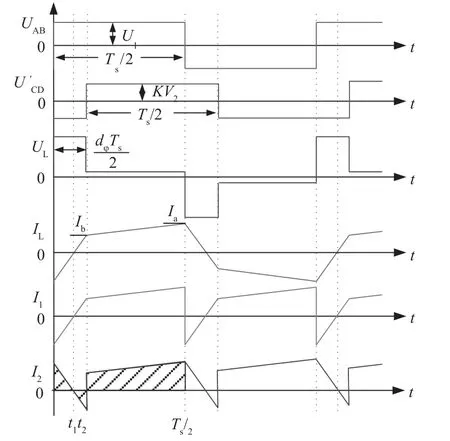
图2 移相控制方式的工作波形
由于移相角不是直接的控制量,这里将移相角φ用其所对应的占空比dφ表示,φ和dφ满足下列关系式:

其功率传输的表达式为:
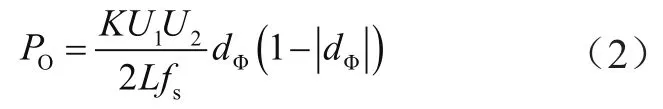
式中,φ为移相角,dφ为移相角φ所对应的占空比,π为圆周率,PO为功率,K为变压器原副边的匝比,U1为t1对应的电压,U2为t2对应的电压,L为电感量,fs为开关频率。从式(2)可知,当0<dφ<1,功率正向传输;当-1<dφ<0,功率反向传输[11]。
2 DAB的小信号建模
2.1 DAB的电路平均模型
由图1可知,DAB的开关网络由原副边全桥结构、能量传输电感以及变压器构成,开关网络的输入量为Dφ,输出变量为I1、I2。下面利用电路平均法进行建模。
定义Ts/2时刻电感电流的值为Ia,t2时刻电感电流的值为Ib,根据法拉第电磁感应定律,可以给出Ia、Ib的表达式,分别为:

式中,Ia为Ts/2时刻电感电流的值,Ib为t2时刻电感电流的值,Ts为开关周期。
求解式(3)和式(4)可得:

从图2可知,Ia/Ib=t1/t2,且t1+t2=dφTs/2,结合式(5)和式(6)可以求出:
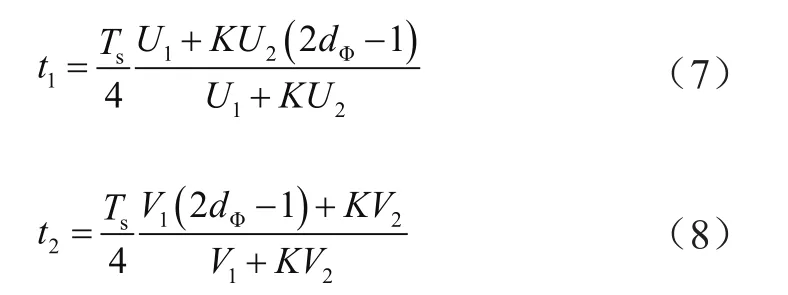
I2是周期为Ts/2的周期信号,在[0,Is/2]时间段内,I2的表达式为:
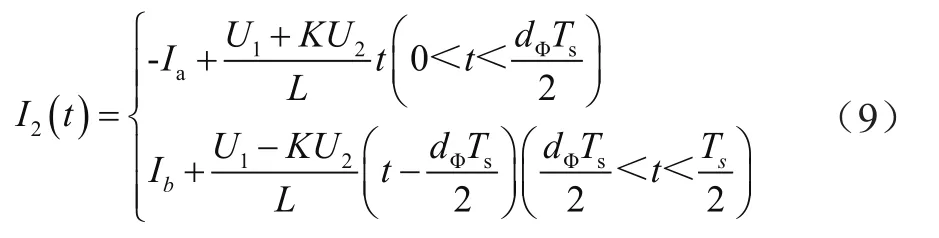
式中,I1、I2为电流输出变量。
由图2可知,I2的周期平均值为图中阴影部分的面积再除以Ts/2,即:
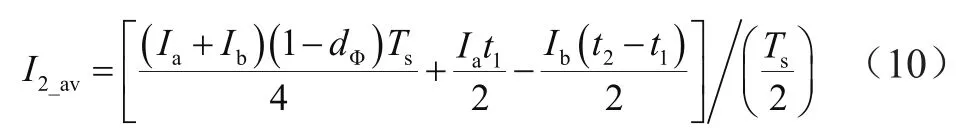
式中,I2_av为I2的周期平均值。
将式(5)~式(8)代入式(10),整理可得:
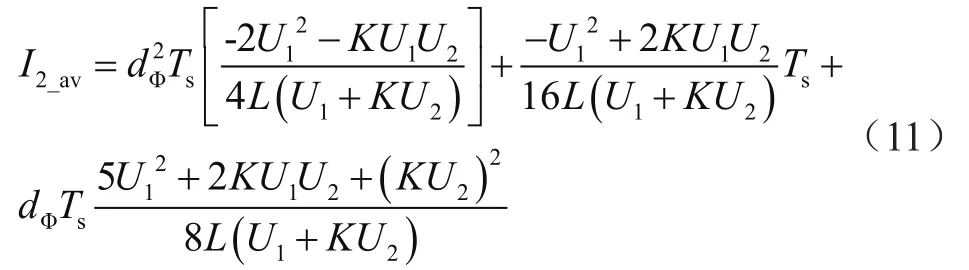
对I2_av和dφ叠加小信号扰动,即:

式中,Dφ、i2_av分别表示dφ、I2_av的稳态值,Φ为移相角φ所对应的占空比的估计值,2为电流输出变量的估计值。
将式(12)和式(13)代入式(11),抵消方程两侧的直流量,并忽略方程中的高阶小量,可得线性化的小信号方程为:
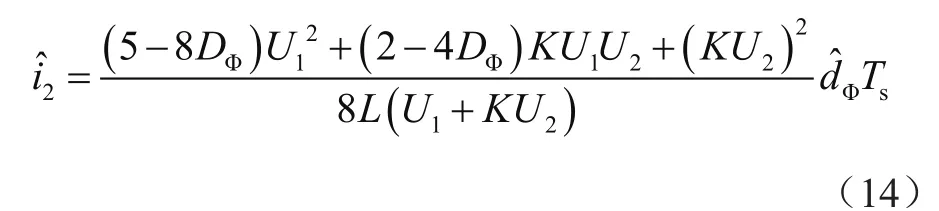
由此可得移相角到电感电流的传递函数为:
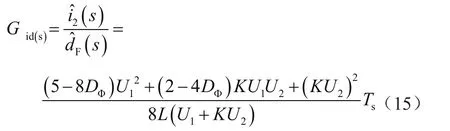
式中,Gid(s)为移相角到电感电流的传递函数。
可见,在双有源全桥双向变换器中,移相角到输出侧电流的小信号传递函数为一个比例环节,且该比例值由输入电压、输出电压、电感值以及移相角共同决定。
进一步的,根据图1可知,双有源全桥双向直流变换器的输出电压表达式为:

结合式(15))和式(16)即可得到移相角到输出电压的小信号传递函数为:

式中,Gvd(s)为移相角到输出电压的小信号传递函数。
可见,双有源全桥双向直流变换器中,移相角到输出电压的传递函数为一阶惯性环节,其转折频率由负载电阻以及输出滤波电容确定。
2.2 传递函数的仿真验证
利用SIMPLIS电路仿真软件所提供的网络分析仪,可以方便地测量变换器的传递函数。本文在SIMPLIS仿真环境下搭建了双有源全桥双向直流变换器的仿真电路,具体的电路参数见表1。

表1 双有源全桥双向直流变换器的仿真参数
利用SIMLIS软件,分别测量了移相角到电感电流的传递函数Gid(s)和移相角到输出电压的小信号传递函数Gvd(s)的Bode图。测量结果与模型的计算结果如图3所示。可见,计算结果与测量结果非常吻合,验证了模型的正确性。

图3 Gid(s)和Gvd(s)传递函数的仿真和计算结果
3 双有源全桥双向直流变换器的闭环设计
对于电压型控制的双有源全桥双向直流变换器,其闭环控制框图如图4所示。

图4 电压型控制双有源全桥双向直流变换器的闭环控制框图
根据图4,环路增益表达式为:

式中,H为电压采样系数,Um为PWM调制器的锯齿波峰峰值,Gc(s)为调节器的传递函数[12,13]。
在进行闭环设计时,若选择变换器的截止频率为fc,相位裕度为PM,则在fc处有:

工程实践中Gc(s)通常采用PI调节器,即存在:
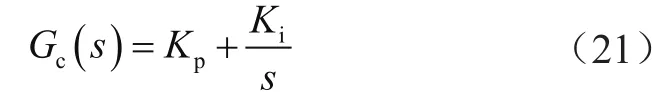
式中,Kp为比例系数,Ki为积分系数[14]。
将式(21)代入式(19)和式(20),可以求得:

根据式(22)和式(23),即可方便的求得PI调节器的参数。
为了保证变换器具有足够的稳定行以及动态性能,本文将截止频率设置在5 kHz(即1/10开关频率),相位裕度设置为45°[15]。针对表1中的样机参数,利用式(22)和式(23)可以求得Kp=21,Ki=660 000。对应的环路增益Bode图如图5所示,可见截止频率与相位裕度均满足设计指标。

图5 补偿之后环路增益Bode图
4 实验验证
为了验证理论分析的正确性,在实验室搭建了基于DSP的数字控制双有源全桥双向直流变换器原理样机。
4.1 电路参数设计
按照最高电压应力的1.5倍,电流应力的两倍选取MOSFET,最终选用了英飞凌公司的SPW47N60CFD,其额定电压为600 V,连续导通电流为46 A@25 ℃、29A@100 ℃,导通电阻 RDS(on)为 0.08 Ω[16]。
本实验的控制电路采用TI公司生产的数字信号处理芯片TMS320F2812作为核心控制单元。TMS320F2812通过内部事件管理器输出8路带死区的互补PWM信号,PWM信号幅值与DSP芯片的供电电压相同,为3.3 V。将这8路PWM信号经过缓冲器74LS244转换为幅值为5 V的TTL电平信号,然后再经过IXYS公司生产的场效应管专用驱动芯片IXDN604进行功率放大。IXDN604驱动芯片可以同时对两路驱动信号进行功率放大,其输出电流峰值可达4 A,满足实验中功率管SPW47N60CFD的驱动要求。由于桥式电路需要实现驱动隔离,因此将放大后的两路互补信号接驱动变压器,构成双极性驱动。变压器原边一个绕组,副边两个绕组,分别驱动一个桥臂的上、下管,具体的控制电路如图6所示。实际中,R0取1 Ω,R1和R2取8.2 Ω,加速关断二极管DQ1、DQ2选用肖特基二极管IN5819。

图6 控制电路电路图
4.2 实验结果
根据所给出的PI调节器参数,对双有源全桥双向直流变换器进行实验验证,所得的实验波形如图7所示。图7(a)为10%的波形,图7(b)为满载波形。图中,从上到下依此是原边桥臂中点电压波形UAB、副边桥臂中点电压UCD以及电感电流IL的实验波形。从UCD可知,无论在轻载还是满载情况下,变换器的输出电压均能稳定在324 V,验证了闭环设计的有效性。
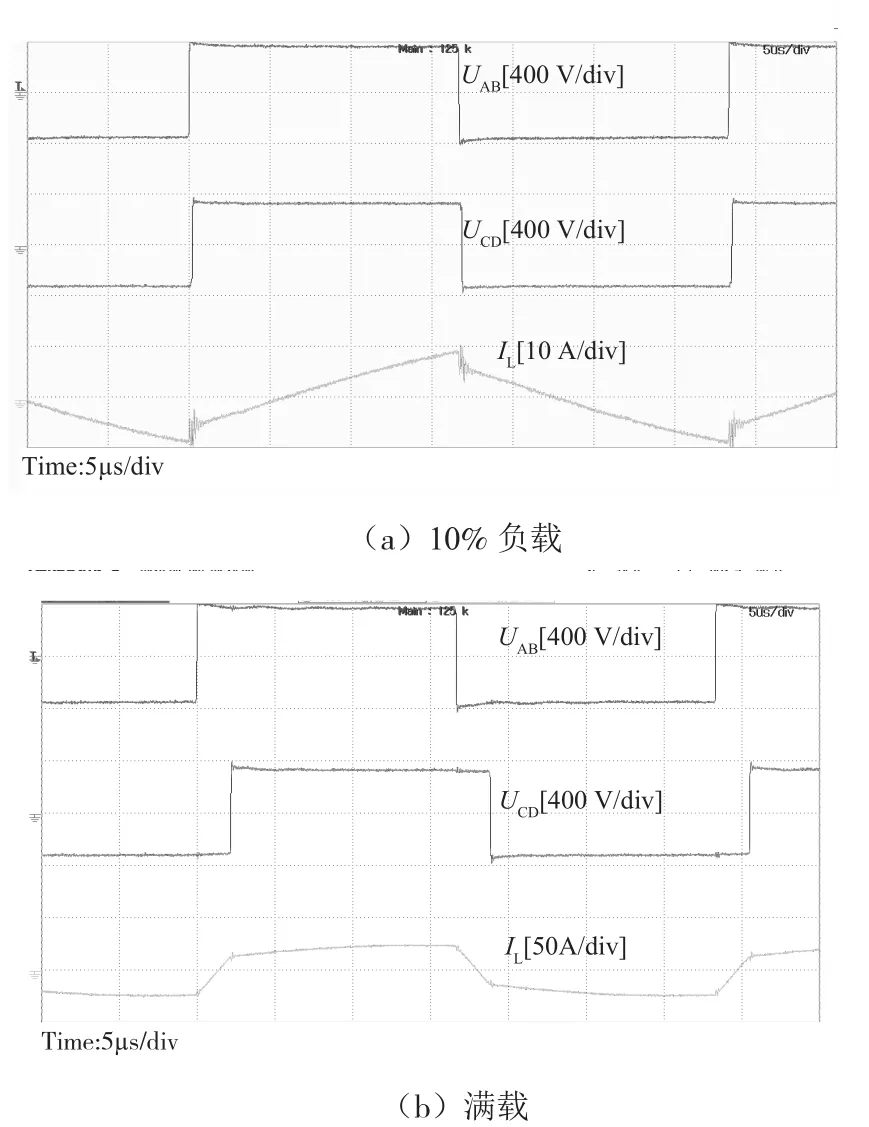
图7 不同负载情况下DAB的工作波形
5 结 论
本文研究了DAB的数学模型。首先,采用电路平均法建立输出侧电流与移相角之间的传递函数。其次,基于该结果得到移相角到输出电压的传递函数,该传递函数为一阶惯性环节,且转折频率由输出滤波电容和负载电阻确定。再次,通过SIMPLIS软件仿真验证所得模型的传递函数,并基于所得模型进一步进行了PI调节器设计。最后,在实验室搭建一台6 kW的DAB原理样机,验证理论分析的正确性。
