基于大数据平台的集油管道运行特性预测方法研究

李玉春 李治东 李越 孟岚 姚毅立 孙巍 成庆林 孙海英

1大庆油田设计院有限公司

2东北石油大学

3大庆油田有限责任公司第五采油厂

随着信息技术的高速发展，工程上获得数据的难度越来越低、手段越来越多、效率越来越高，从而导致信息数据库的规模不断增大，其复杂程度也持续增大，演变成为庞大复杂的信息数据体系[1-3]。因此有必要基于大数据平台，针对双管掺水流程建立水力热力回归预测模型[4-6]。

目前，很多学者在管道预测方面进行了大量研究。张青松利用人工神经网络强大的非线性映射能力，建立了人工神经网络混油黏度预测模型，该方法误差小，并能够同时考虑温度变化等因素的影响[7]；高山卜利用BP神经网络建立输油管道的能耗预测模型，其预测误差不超过4.06%，为管输能耗提供了新的预测方法[8]；李建松建立灰色神经网络预测模型对输油管道运行费用进行预测，结果表明预测模型精度高，计算量小，收敛速度快[9]；林冉用人工神经网络建立了管道耗能的预测模型，该模型的计算结果相对偏差在±5%以内，满足工程实际需要，为预测管道的能耗总量提供了便利[10]；李树杉根据大数据思想，基于管道SCADA 系统提供的大量管道运行历史数据，利用神经网络构建了管道预测模型，并用其替代传统的管道数学模型，计算油品的温度和压力，求解能耗优化的目标函数，得出优化方案，提高了方案的准确性和实用性[11]。

通过调研发现，采用传统理论公式计算得到的管道传热系数以及水力摩阻系数通常与现场实际情况不符[12-13]，因此构建了双管掺水流程大数据平台。运用水力热力基础运行参数，通过python语言编程，分别建立了BP 神经网络管线传热系数和水力摩阻系数的预测模型，并通过迭代自修正权重和偏置，经过参数的降维处理校正了传统的计算公式，最终对所得出的预测模型进行了验证，其满足实际工程标准，可以用来计算管线的节点参数，为计算管线节点参数奠定了基础，也为后续的预测管线能耗提供了数据保障。

1 大数据预测模型建立

1.1 大数据平台

大数据平台由三个数据集构成：初始数据集、存储数据集和应用数据集。双管掺水流程大数据平台的特点是数量大、种类多、更新快、季节性明显。数量大：数据“量的大小”是直接影响所建立预测模型准确程度的主要因素之一，数据越多，预测模型的精度越高；种类多：如管道起点和终点压力、起点和终点温度、环境温度、管线输量等，通过多个参数得到多元预测模型，并向水力热力理论公式靠拢，增强了预测模型的理论性；更新快：各基础参数的采集采用数字化技术，按设定频次定时采集，不间断更新；季节性明显：管线各基础参数，尤其是热力参数受季节变化影响较大，由于冬夏气温差异较大，管线运行参数的变化也较为明显。双管掺水流程大数据平台的结构与特点如图1所示。

图1 大数据平台结构特点Fig.1 Structural characteristics of big data platform

1.2 热力预测模型

基于传统传热系数的计算方法，即轴向温降基本公式，也称作舒霍夫温降公式[14]，可以看出采出液温度的变化受土壤环境温度、管径、管道长度、流量、采出液比热容等参数的影响。舒霍夫温降公式表达式为

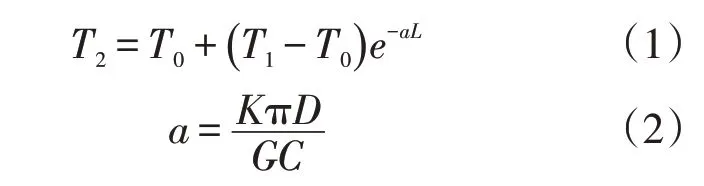
式中：T2为管线终点温度，℃；T0为环境温度，℃；T1为管线起点温度，℃；L为管道长度，m；a为参数，无量纲；G为油井产液量，kg/s；C为井口采出液比热容，J/(kg·℃)；D为管道直径，m；K为管道传热系数实际值，W/(m2·℃)。

由上式得出管线传热系数的基本公式（3）。

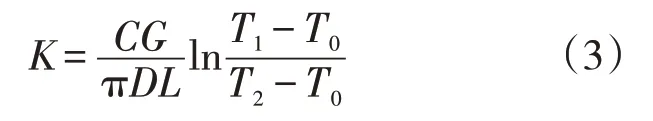
但在现场实际运行过程中，不同管道的传热系数还与管道内结蜡厚度、保温层完整性、管道直径、土壤温度等数据相关。因此，仅通过理论公式的计算难以满足现场的实际应用，需要建立以油田数字系统为基础的大数据平台，将难以直接测量的多组固定参数降维处理[15]。对于同一条管道来说，C、π、D、L等参数是固定不变的，因此将这些参数全部融合到新的参数A中，同时，由于拟合管道传热系数的目的是计算管道终点的温度，因此利用参数A、B将模型中的T2隐去，用新的回归关系式的形式来表示简化后的热力模型为

式中：A、B均为待回归参数，无量纲。

1.3 水力预测模型

在水力参数方面，主要针对水力摩阻系数进行研究，水力摩阻系数是与起终点压力、混输流量、管道外径和管道长度相关的参数，将混输水力模型简化为与起点和终点压力、流量相关的数学模型，如式（5），得到水力摩阻系数的理论公式，从而对此理论公式进行修正，最后得出实际管线水力摩阻系数的回归模型。

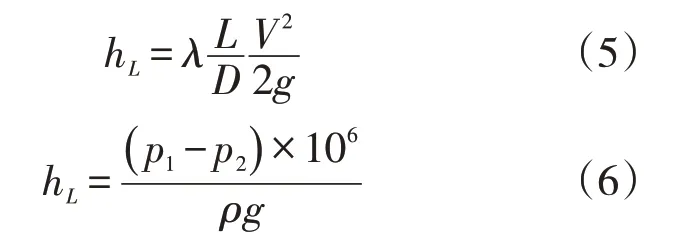
联立式（5）与式（6）得

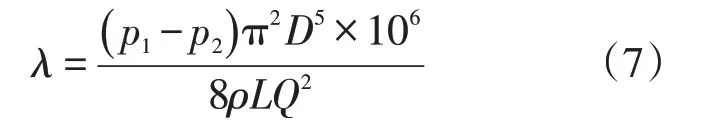
式中：λ为管线水力摩阻系数；L为管道长度，m；D为管道内径，m；V为混合物平均流速，m/s；p1、p2分别为管线起点和终点压力，MPa；Q为井口产液量，m3/s；g为重力加速度，m/s2；ρ为井口采出液密度，kg/m3。

同管道传热系数，对于同一条管道来说，ρ、π、D、L等参数是固定不变的，因此将这些参数全部融合到新的参数A′中。同时，由于拟合水力摩阻系数的目的是计算管道终点的压力，因此利用参数A′、B′将模型中的p2隐去，用新的回归关系式的形式来表示简化后的水力模型为

式中：A′、B′均为待回归参数，无量纲。

由于Q的数量级较小，拟合后系数的数量级极小，因此将Q的单位改为m3/h后再进行拟合。

2 BP神经网络模型

2.1 BP神经网络模型建立

双管掺水流程水力热力运行参数的BP 神经网络模型具体搭建过程如下：

（1）建立大数据平台。进行收集数据，数据预处理，大数据清洗、分类与储存等。

（2）数据集划分。从建立好的大数据库中提取待预测的数据集，将数据集分为训练集和测试集。先用训练集训练模型，再通过测试集对训练的模型进行测试，导入训练集数据，检验模型是否合理。

（3）确定隐含层数及神经元数。本项目在以往的BP 神经网络模型的基础上进行简化，建立三层神经网络模型，设置单隐层，且该隐层仅设置一个神经元，输入层和输出层也各含一个神经元。

（4）设置超参数。设置神经网络进行预测的学习率、迭代的总次数和输出预测结果的步长。这些超参数决定了预测速度及结果的准确度。

（5）构造损失函数。以训练集中数据的预测值和实际值的二维欧式距离之和，即总误差和最小构造损失函数作为神经网络的训练模型。

（6）训练模型。根据初始设置超参数训练神经网络模型，通过BP 神经网络中的误差反向传播算法修正权重w和偏置b，直至损失函数达到最小值，认为此时的w和b为该组数据集下最右的权重与偏置。

（7）得到预测模型。根据步骤（6）中预测得到的w和b，建立转油站系统管线运行水力热力参数—管线传热系数和水力摩阻系数的预测模型。

（8）检验模型。导入测试集数据，通过预测的模型计算得出计算值，再与实际值进行比较，检验误差结果是否在设置的运行范围内。

模型具体搭建过程如图2所示。

图2 BP神经网络模型流程Fig.2 BP neural network model flow

2.2 BP神经网络模型求解

对大庆油田某计量间及其所辖6口采油井运用上述搭建的BP 神经网络模型，采集超过700 组现场运行数据，训练管线传热系数和水力摩阻系数，计算方程中的权重、偏置等参数。各管线传热系数与水力摩阻系数计算模型的训练结果见表1。

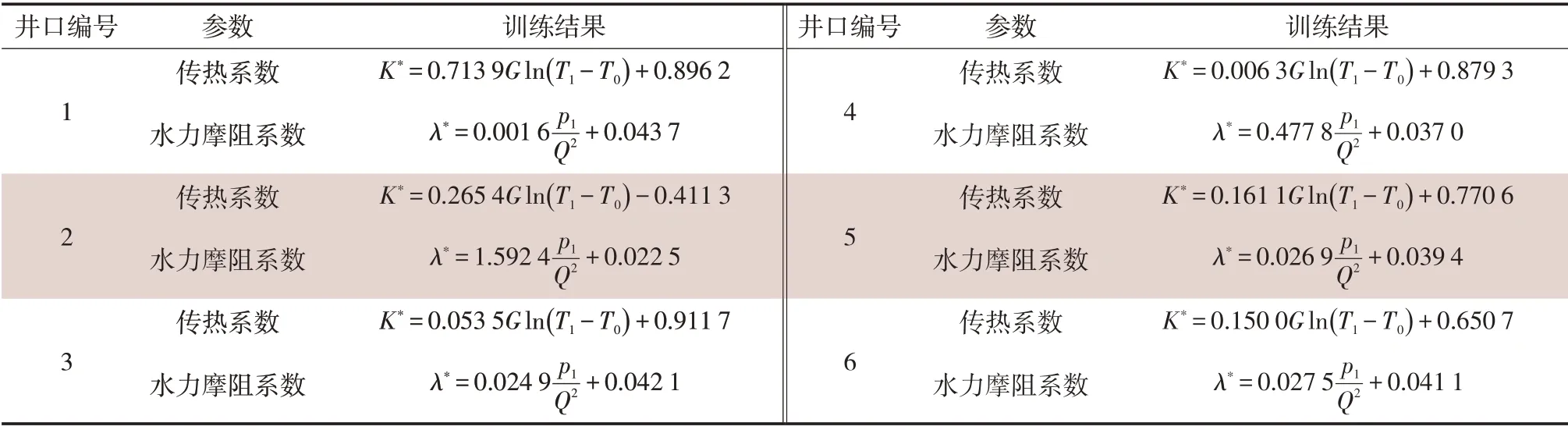
表1 各管线计算模型训练结果Tab.1 Training results of each pipeline calculation model

经过以上步骤可以得出管线传热系数和水力摩阻系数的计算方程。为检验计算方程的准确性，通过计算预测值与实际值之间的偏差，从客观数字的角度上分析预测结果的准确性。引入平均相对误差概念，平均相对误差=，根据平均相对误差的计算值是否在工程允许的范围内来判断预测方程的可行性。通过实际值和预测方程得出的计算值来计算该组数据的平均相对误差，绘制各训练结果的误差曲线，来判断预测方程的准确程度。各管线传热系数与水力摩阻系数的相对误差如表2所示，误差曲线如图3与图4所示。

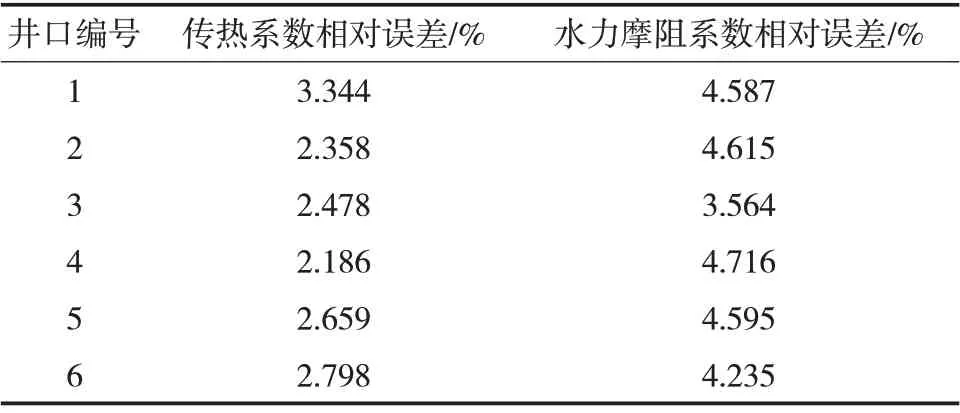
表2 各管线计算模型相对误差Tab.2 Relative error of each pipeline calculation model

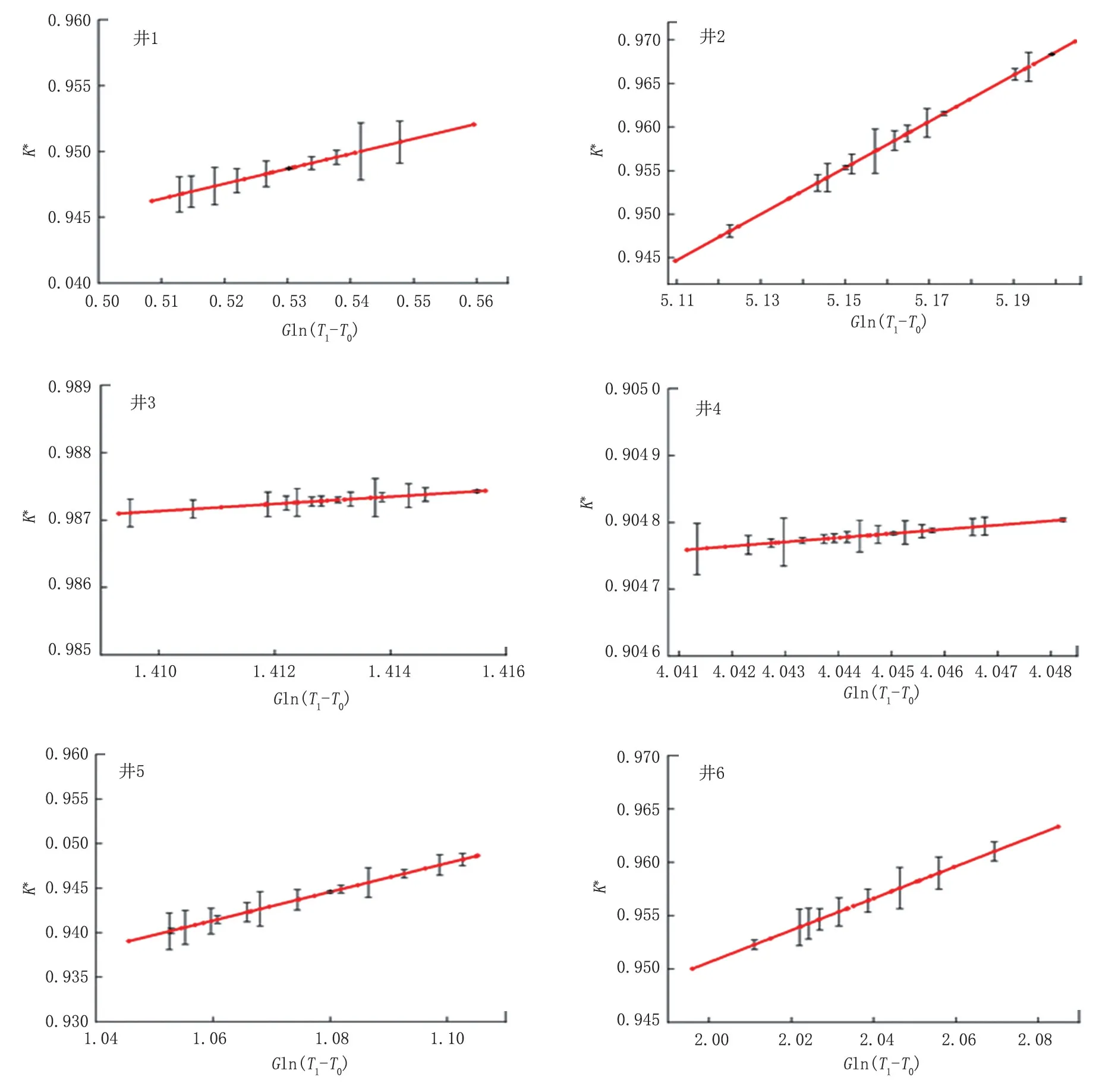
图3 传热系数误差曲线Fig.3 Error curve of heat transfer coefficient

图4 水力摩阻系数误差曲线Fig.4 Error curve of hydraulic friction coefficient

通过分析管线传热系数误差曲线可以看出，存在一个新参数ς=Gln(T1-T0)，使得管线传热系数随之变化。6口采油井的管线传热系数K*均随着的ς的增大而增大，呈线性关系。管线传热系数相对误差最小的是井4，为2.186%，而相对误差最大的是井1，为3.344%，均满足工程计算所需的精度。

通过分析水力摩阻系数误差曲线可以看出，存在一个新参数σ=，使得水力摩阻系数随之变化。6口采油井集输管线的水力摩阻系数λ*均随着σ的增大而增大，呈线性关系。水力摩阻系数相对误差最小的是井3，为3.564%，而水力摩阻系数相对误差最大的是井4，为4.716%，均满足工程计算所需的精度。

经计算，各集输管道的管线传热系数和水力摩阻系数的平均相对误差均在工程允许的误差范围内，因此认为此BP 神经网络模型对于管线传热系数以及水力摩阻系数计算方程的预测准确性高，回归后的方程可以用于该计量间集输管线的实际运行参数计算。

3 结论

构建了双管掺水流程大数据平台，通过python语言编程，建立了BP 神经网络管线传热系数和水力摩阻系数的回归预测模型，并通过迭代自修正权重和偏置，经过参数的降维处理校正了传统的计算公式。对所建立的神经网络模型进行验证，发现大庆油田某计量间所辖6口井集输管道的管线传热系数和水力摩阻系数的平均相对误差均小于5%，满足实际工程计算的精度，因此所建立的模型可以用来计算现场管道实际运行参数，也为各管段的节点计算以及后期的能耗预测分析打下了坚实的数据基础。