试卷设计的聚类算法

张启东

（沈阳理工大学信息科学与工程学院 辽宁省沈阳市 110159）

1 引言

在普通高校推进教考分离改革背景下，注重学生分析问题、解决问题能力的培养和考核，将以题库制为主要试卷设计形式，实行教考分离命题方式，迫切要求建立符合课程特点，形式多样的考试评价制度，提高教育评价的科学性、专业性和客观性，突出相应专业能力和实践应用能力考查。如何选择和设计一个合适的高效试卷设计[1-5]算法是教考分离的关键手段。

试卷设计的难点是如何调整试题的难度和区分度，已有技术是从课程的考试大纲和试题库建立试卷的设计模型，在试卷生成算法中，已被探讨的聚类方法有基于时空特征的聚类方法[6]，基于关联灰色趋势的聚类方法[7]，基于模糊性的聚类方法[8]，基于最优目标的模糊性聚类方法[9]等，以及基于传统的K均值法[10]、高斯基函数[11]和神经图模型[12]等聚类方法。

本文从试题得分的随机性特征参数出发，导出试卷及格率,以控制试卷得分的及格率为目标和以难度系数和区分度等为约束条件建立试卷的设计模型，用一种简化方法调整试题的难度和区分度，用一种聚类基函数从试题库中选择试题和用聚类算法生成试卷, 本文聚类基函数能够方便地调整试题的难度系数和变差系数。

2 试卷设计模型

2.1 及格率度量指标

对于一套由N道试题组成的试卷，若第k道试题权重分数、难度系数和变差系数分别为ωk、δk和γk，则试卷的可能得分s可由式（1）表示。

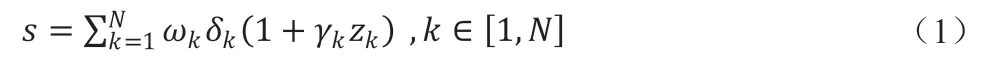
式中的zk是0-1正态分布的随机变量，用于描述第k道试题得分的离散性。

难度系数是试题的一种难度指标；变差系数是试题的一种区分度指标。

若在试卷中的题目互不相关，则试卷得分的平均值μs和标准差σs可由式（2）和（3）分别算出。

引入度量试卷及格率的指标变量β，试卷及格率的指标变量值用式（4）表示。

式中的c是试卷得分的及格分数线，为确定性变量。容易确定试卷的及格率Pr=Φ(β)。试卷的及格率会随着试卷平均得分和及格分数线之差增减会变大或小，试卷的及格率会随着试卷得分标准差的增减会变小或大。

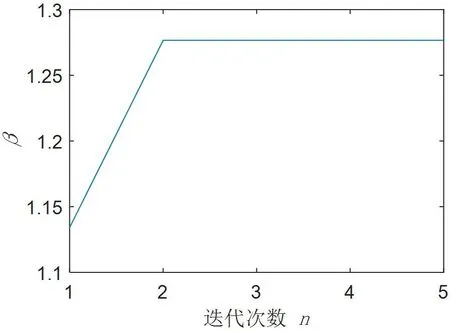
图1：及格率指标与迭代次数关系

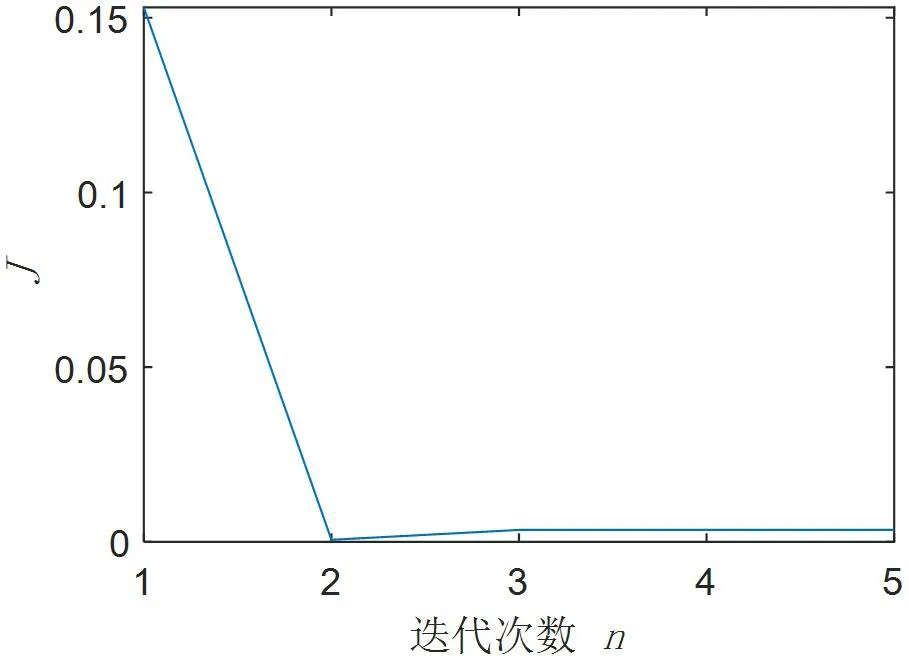
图2：设计目标值与迭代次数关系

采用试卷及格率的度量指标设计试卷，设计试卷的问题可以归结为在可行域调整试题的难度系数和区分度，使试卷得分的及格率达到预期的要求。

式中的Ωk为第k道试题的可行域。试题设计的可行域可以按试卷难度、区分度、课程考核知识点及其覆盖率、试题的重复率和雷同率指标确定。

2.2 聚类基函数

直接用式（5）设计试卷不够简单和方便，下面给出基于聚类基函数的方法。

用试题的归一化灵敏度系数将试卷得分标准差的计算公式拟线性化。若第k试题的灵敏度系数αk为：

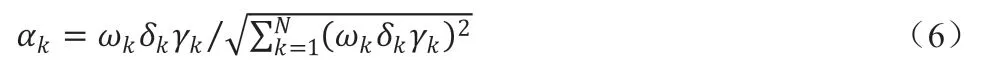
灵敏度系数是试题对区分度的影响因子。一般来说，在试卷中的每个试题，都应对试卷的区分度有明显的影响。一般情况下，在由N道试题组成的一套试卷中，每道试题的归一化灵敏度系数应尽可能趋近于

表1：试题的候选试题

将试卷的及格分数线规格化。若规格化及格分数线c0为：

利用式（6）-（7）和式（2）-（4），可将式（5）改成写成下述形式：

式中：J为设计目标的变量值；ψ(·)为聚类基函数，由式（9）确定。

聚类基函数的值可以度量试题的设计参数对试卷设计目标的影响程度。若按约束条件使每道试题的聚类基函数ψ(δk,γk)趋近于0，则生成的试卷已逼近试卷的预期设计目标。采用聚类基函数从试题库中选择试题和生成试卷也比较简单和方便。

3 试卷生成的聚类算法

按约束条件用逐次迭代来逼近试卷的设计目标和生成试卷。基于聚类基函数的生成试卷的迭代算法概括如下：

步骤1 给出在试卷中的试题数量、及格分数线或规格化的及格分数线、以及预期的及格率指标，并为每个试题分配权重分数等。

步骤2 按试题的可行设计域从试题库中随机选取N组试题，每组试题至少有一道候选试题；按候选试题数量由少到多的顺序，为试题组编制从1到N的序号；将每组试题的灵敏度系数均设置为

步骤3 设置迭代计算精度ε；迭代计数器变量n初始化，n=0；设置试卷设计的目标值J(0)=∞。

步骤5 先用式（6）算出每组候选试题的灵敏度系数；最后用式（8）算出试卷设计的目标值J(n+1)。

步骤6 若|J(n+1)-J(n)|>ε，则令n=n+1，并转至步骤4，否则输出试卷设计结果。

一般情况下，通过调整试题的权重分数、难度系数和区分度的界值，能够得到难度适中、及格率符合预期要求的一套试卷。

4 实验结果

某套试卷由试题A、B和C组成。试题A、B和C的权重分数分别为4、4和2；考试及格分数线c=6，归一化及格分数线c0=0.6；考试及格率为90%以上，预计及格率预期指标β=Φ-1(0.90)≈1.28。试题的难度系数和变差系数按试卷的难度和区分度确定。

设计结果：及格率指标与迭代次数关系见图1，设计目标值与迭代次数关系见图2。

及格率预期指标β=1.28，预期的考试及格率为90%。当迭代3次时，生成试卷预期的及格率指标已符合试卷的设计指标；采用本文的聚类算法迭代生成试卷时，可以较快的收敛速度趋近于试卷的设计目标值。

在设计试卷时，按关系式γ≤(1⁄δ-1)⁄β选择候选试题可以得到较好的设计结果。

5 结语

本文以试题得分的正态概率分布特征出发，导出试卷及格率的度量方法，以预期的及格率为目标建立了试卷的设计模型，给出一种聚类基函数和基于聚类基函数的试卷生成算法，实验结果表明，本文聚类基函数能够按难度和区分度等约束条件，从试题库中选取题目和生成难度适中、及格率符合预期要求的试卷。