基于PSO-SVM的水工隧洞施工成本预测
2021-09-22刘英杰聂章琴王博许亚辉
刘英杰 聂章琴 王博 许亚辉

摘 要:为了对水工隧洞工程施工成本进行精确预测,从工程、环境、市场以及管理4个方面分析了水工隧洞施工成本影响因素,构建了水工隧洞施工成本影响因素量化方法。采用粒子群算法(PSO)优化支持向量机(SVM)模型中的惩罚因子C和核函数参数g,建立基于PSO-SVM的水工隧洞施工成本预测模型。对比SVM模型的预测结果发现,PSO-SVM模型的平均绝对百分比误差和均方根误差更小,训练速度更快,预测效果更好。
关键词:成本预测;支持向量机;粒子群算法;水工隧洞
中图分类号:TV554
文献标识码:A
doi:10.3969/j.issn.1000-1379.2021.09.031
引用格式:刘英杰,聂章琴,王博,等.基于PSO-SVM的水工隧洞施工成本预测[J].人民黄河,2021,43(9):160-164.
Construction Cost Prediction of Hydraulic Tunnel Based on PSO-SVM
LIU Yingjie1,2,3, NIE Zhangqin1, WANG Bo1,2,3, XU Yahui1
(1.School of Water Conservancy, North China University of Water Resources and Electric Power, Zhengzhou 450046, China;
2.Collaborative Innovation Center of Water Resources Efficient Utilization and Support Engineering, Zhengzhou 450046, China;
3.Henan Key Laboratory of Water Environment Simulation and Treatment, Zhengzhou 450046, China)
Abstract: In order to accurately predict the construction cost of hydraulic tunnel engineering, this paper analyzed the influencing factors of hydraulic tunnel construction cost from four aspects of engineering, environment, market and management, and established a quantitative system of influencing factors of hydraulic tunnel construction cost. Particle Swarm Optimization (PSO) was used to optimize the penalty factor C and kernel function parameter G in the support vector machine (SVM) model, and the construction cost prediction model of hydraulic tunnel based on PSO-SVM was established. Compared with the prediction results of SVM model, the average absolute error percentage and root mean square error of PSO-SVM model are lower, the training speed is faster and the prediction effect is better.
Key words: cost forecast; support vector machine; particle swarm optimization; hydraulic tunnel
水工隧洞工程具有施工條件复杂、工期长、技术难度高、投资规模大等特点。准确预测水工隧洞成本是实现水工隧洞成本管理的首要任务。成本预测方法包括线性回归法、时间序列法、灰色理论、神经网络、支持向量机(SVM)等。线性回归法认为工程成本是线性变化的,时间序列法是研究历史数据随时间的推移而发生的变化,而水工隧洞成本受施工条件和气象条件等多因素的限制是非线性和不确定的;灰色理论通过分析各影响因素间的关联度来预测成本,适合低维数据;神经网络的优化算法为误差梯度下降法,但容易陷入过拟合、局部最优等问题。SVM算法可以避免过拟合,在样本数据较少的情况下也能进行预测,在成本预测领域被广泛使用,如:秦中伏等[1]将主成分分析法和支持向量机相结合,对住宅工程成本进行了预测;Zhang Y等[2]构建了基于随机森林-支持向量机的工程成本预测模型;李静等[3]通过遗传算法优化支持向量机,完成了对输电塔造价的预测;乔国华等[4]构建了基于遗传算法的最小二乘支持向量机模型,对变电站全寿命周期成本进行了预测;刘飒等[5]构建了基于主成分分析法和支持向量机的企业成本预测模型。SVM的参数选择与模型的训练效果有密切的关系,选择参数的传统方法用时太长,且很难得到全局最优解。粒子群优化(PSO)算法在优化领域中被大量使用,取得了良好的效果,如:黄敏等[6]基于粒子群算法优化支持向量机构建了山区公路隧道成本预测模型;高昆仑等[7]通过粒子群算法优化支持向量机,预测了未来网络安全态势。本文针对SVM选择参数时存在的盲目性问题,提出利用PSO算法优化其模型参数,对水工隧洞施工成本进行预测。
1 水工隧洞工程施工成本影响因素分析
1.1 影响因素识别
水工隧洞工程施工成本的影响因素很多,一般而言应考虑工程方面、环境方面、市场方面和管理方面的影响因素[8-15]。工程方面包括压力状态、长度、横断面面积、横断面形状、衬砌类型、掘进方式等;环境方面包括围岩类别、气象条件、场地施工条件、场内外临时交通状况等;市场方面包括人工、材料、机械的价格及其变化趋势;管理方面包括业主管理水平、承包商管理水平、监理管理水平、施工工期等。
1.2 主要影响因素量化
水工隧洞工程施工成本的影响因素量化方法见表1。
2 基于粒子群算法的支持向量机成本预测模型
2.1 支持向量机回归模型
SVM基于结构风险最小化,使用核函数将数据映射到高维空间,寻找其最优超平面。
假设样本数据D={(xi,yi)|i=1,2,…,n}(其中:xi为第i个样本的输入值,yi为输出值),SVM找到一个与y相近的回归函数f(x):
fx=[w,Φ(x)]+b(1)
式中:yi∈R;w为权值系数;Ф(x)为映射函数;b为偏置项。
SVM算法通过求解下述问题确定w和b:
min12‖w‖2+C∑ni=1(ξi+ξi)
s.t.yi-[w,Φ(x)]-b≤ε+ξi
[w,Φ(x)]+b-yi≤ε+ξi
ξi、ξi≥0(2)
式中:ξi、ξi*为松弛变量;C为惩罚因子,C>0;ε为容许误差。
引入拉格朗日乘子可得:
L=12‖w‖2+C∑ni=1(ξi+ξ*i)+ ∑ni=1λi[yi-wΦ(xi)-b-ε-ξi]+∑ni=1λ*i[wΦ(xi)+b-yi-ε-ξ*i]-∑ni=1(ηiξi+η*iξ*i)(3)
其中λi、λ*i、ηi、η*i≥0。
则上述优化问题的对偶形式为
max[-12∑ni=1∑nj=1(λi-λ*i)(λj-λ*j)K(xi,xj)+
∑ni=1(λi-λ*i)yi-∑ni=1(λi-λ*i)ε]s.t.∑ni=1(λi-λ*i)=0
0≤λi≤C,0≤λ*i≤C(4)
设由式(4)得到的最优解为α={α1,α2,…,αn}、α*={α1*,α2*,…,αn*},则
w=∑ni=1(αi-αi)Φ(xi)(5)
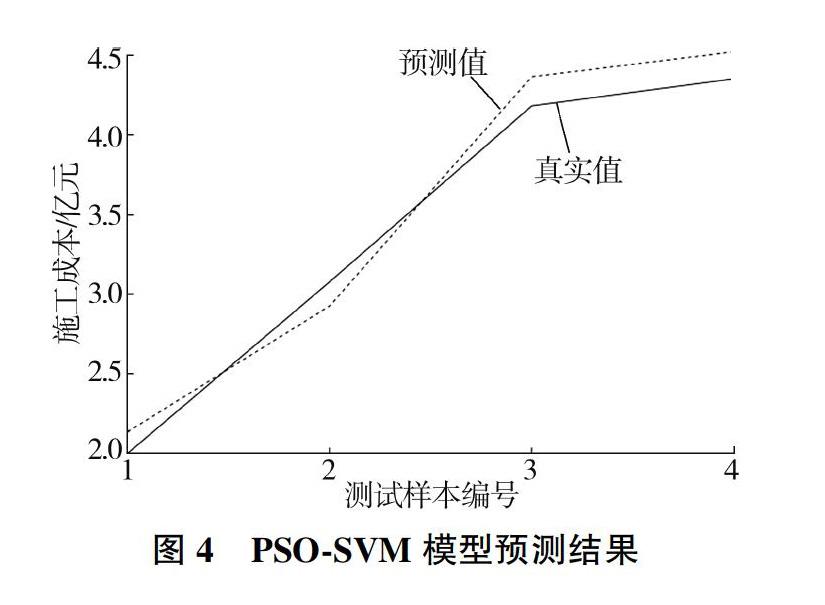
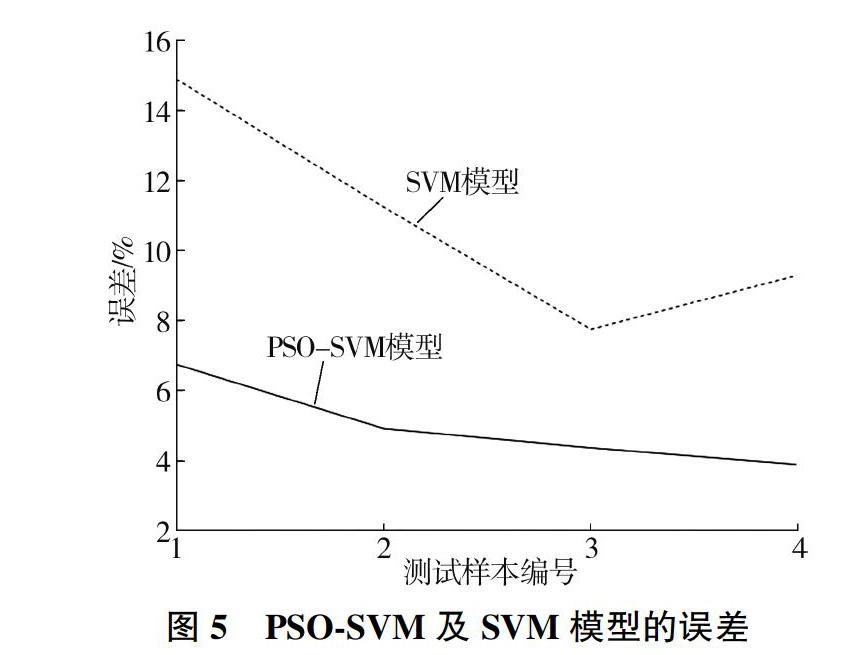
b=1Nnsv{∑0<αi ∑0<αj 式中:Nnsv为支持向量个数。 于是,回归函数为 fx=wΦ(x)+b=∑ni=1(αi-αi)Φ(xi)Φ(xj)+ b=∑ni=1(αi-αi)K(xi,xj)+b(7) 其中K(xi,xj)为核函数,K(xi,xj)=Ф(xi)Ф(xj)。 径向基函数为 kRBF(xi,xj)=exp[-g(xi-xj)2] (g>0)(8) 式中:g为核函数方差,g=1/(2σ2)(σ为核函数的宽度参数)。 2.2 粒子群优化算法 粒子群算法(PSO)通过不断迭代找到最优解。设在一个D维空间中存在n个粒子构成的群体x={x1,x2,…,xn},第i个粒子的位置为xi=(xi1,xi2,…,xiD),速度为vi=(vi1,vi2,…,viD),个体极值为Pi=(Pi1,Pi2,…,PiD),群体极值为Pg=(Pg1,Pg2,…,PgD),在不断迭代过程中,根据式(9)和式(10)更新xi和vi,通过适应度函数F求适应度值并更新个体极值Pbest和群体极值Gbest,达到最大迭代次数或适应度值小于设定值时迭代终止。 xk+1iD=xkiD+vk+1iD(9) vk+1iD=ωvkiD+c1r1(PkiD-xkiD)+c2r2(PkiD-xkiD)(10) 式中:ω為惯性权重因子;k为当前迭代次数;viD为速度;c1和c2为加速度因子;r1和r2为在[0,1]区间的随机数。 2.3 基于粒子群算法的支持向量机成本预测流程 基于PSO-SVM的水工隧洞施工成本预测流程如图1所示。 步骤1:收集水工隧洞的历史施工成本数据并构成数据集,把数据集分为训练集和测试集。 步骤2:运用MATLAB软件的mapminmax函数对数据进行归一化处理。 步骤3:设定粒子群的参数,得到粒子的位置与速度。 步骤4:根据粒子目前的位置,得到C、g值,利用svmtrain函数创建SVM预测模型,求解粒子适应度值,对比PkbestiD,如果现在的值更接近设定值则替代PkbestiD。 步骤5:对比每个粒子的适应度值与群粒子的适应度值,如果群粒子的适应度值大于每个粒子的适应度值,则用PkbestiD替代GkbestiD,根据式(9)、式(10)更新粒子的位置与速度。 步骤6:判断是否达到终止条件,如果达到则PSO计算结束,输出最优值;如果未达到则重复步骤4。 步骤7:将PSO找到的参数C、g代入SVM模型重新训练,得到较优的SVM模型。 步骤8:利用svmpredict函数进行预测、mapminmax函数将结果反归一化,得到水工隧洞施工成本预测结果。 2.4 预测结果分析指标 选取平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为预测结果分析指标。MAPE与RMSE计算公式分别为 MAPE=1N∑Ni=1yi-y*iyi×100%(11) RMSE=1N∑Ni=1(yi-y*i)2(12) 式中:N为样本数目;yi和yi*分别为第i个样本的实际值与预测值。 3 案例分析 3.1 水工隧洞成本数据收集 共收集了22个水工隧洞工程项目的成本数据,根据表1对原始数据进行量化,结果见表2。为了验证基于PSO-SVM的水工隧洞项目成本预测模型的可靠性和准确性,将22个水工隧洞样本分成两组,其中前18个为训练集,后4个为测试集。 3.2 基于SVM的成本预测 利用Matlab软件的mapminmax函数对成本影响因素量化结果进行归一化处理。利用libsvm软件包中的svmtrain函数创建和训练SVM模型,其中SVM模型使用v-SVR的默认参数,利用libsvm软件包中的svmpredict函数进行预测,利用函数mapminmax反归一化,结果如图2所示。 3.3 基于PSO-SVM的成本预测 利用Matlab软件的mapminmax函数对成本影响因素量化结果进行归一化处理;设定PSO的参数,D=2,n=30,c1=1,c2=1.5,ω=1,C∈(0,200),g∈(0,500),F(GkbestiD)=MAPE≤5%,最大迭代次数为500。通过PSO工具箱进行SVM的参数寻优,输出的最优参数值为C=2.426 5、g=0.010 0,其适应度函数如图3所示。由图3可知,预测误差在迭代20次后趋于稳定,在迭代92次时MAPE≤5%。 将PSO工具箱寻优结果代入SVM模型中,利用svmpredict函数进行预测,利用mapminmax函数反归一化,结果如图4所示。 3.4 预测结果分析 PSO-SVM模型的MAPE为4.98%,RMSE为1 930.07万元;SVM模型的MAPE为10.79%,RMSE为3 456.47万元。对比SVM模型的预测结果发现PSO-SVM模型预测的MAPE和RMSE更小,预测更准确。原因是SVM模型预测时使用的是默认参数,最终解可能为局部最优而非全局最优,而PSO-SVM模型中粒子群算法会随着测试样本的输入而动态搜寻支持向量机的最优参数,能够保证预测精度并尽量避免过拟合。 PSO-SVM及SVM模型的绝对误差如图5所示。由图5可知,PSO-SVM模型比SVM模型具有更强的能力。PSO-SVM模型的误差较小,其最大和最小绝对误差分别为6.7%和3.8%,而SVM模型的误差较大,其最大和最小绝对误差分别为14.9%和7.8%。 对比PSO-SVM及SVM模型的训练速度可知,PSO-SVM模型的训练速度较快,最快和最慢训练时间分别为1.5 s和1.9 s,SVM模型的训练速度较慢,最快和最慢训练时间分别为7.8 s和10.6 s。 4 結 论 从工程、环境、市场、管理4个方面分析并量化了水工隧洞成本影响因素,建立了基于PSO-SVM的水工隧洞施工成本预测模型。基于22组水工隧洞工程施工成本数据,利用PSO算法对SVM的参数寻优,得到最优C值为2.426 5,最优g值为0.010 0,建立了基于PSO-SVM的水工隧洞成本预测模型,在Matlab平台上进行预测,得到其MAPE为4.98%,RMSE为1 819.55万元。预测结果表明,与SVM相比,PSO-SVM算法能够在较短的时间内更精确地预测出项目成本,且PSO-SVM模型具有较高的泛化性能。 参考文献: [1] 秦中伏,雷小龙,翟东,等.基于SVM和LS-SVM的住宅工程造价预测研究[J].浙江大学学报(理学版),2016,43(3):357-363. [2] ZHANG Y,FANG S. RSVRs Based on Feature Extraction:a Novel Method for Prediction of Construction Projects Costs[J]. KSCE Journal of Civil Engineering,2019,23(4):1436-1441. [3] 李静,张卓群,李旭.基于GA-SVM的输电塔结构基础施工成本预测[J].施工技术,2016,45(12):100-102,114. [4] 乔国华,郭路遥,吴一敌,等.基于遗传优化最小二乘支持向量机的变电站全寿命周期成本预测模型[J].中国电力,2015,48(11):142-148. [5] 刘飒,万寿义.高新技术企业研发成本的预测模型及方法探讨[J].大连理工大学学报(社会科学版),2021,42(2):42-49. [6] 黄敏,吴立,姚沅.基于支持向量机-粒子群算法的山区公路隧道造价预测[J].公路,2015,60(7):285-288. [7] 高昆仑,刘建明,徐茹枝,等.基于支持向量机和粒子群算法的信息网络安全态势复合预测模型[J].电网技术,2011,35(4):176-182. [8] 刘必君,叶雨辰.基于栈式降噪自动编码器的建筑工程施工成本预测[J].同济大学学报(自然科学版),2020,48(6):922-928. [9] 王颖慧,苏怀智.基于PCA-GWO-SVM的大坝变形预测[J].人民黄河,2020,42(11):130-134. [10] 卢睿,李学伟.工程建筑企业投标中的项目成本预测研究[J].铁道工程学报,2016,33(6):104-109. [11] 李万庆,陈佳琪,孟文清,等.基于BSA-ELM模型的建筑工程施工成本预测研究[J].数学的实践与认识,2019,49(23):10-17. [12] AI D, YANG J. A Machine Learning Approach for Cost Prediction Analysis in Environmental Governance Engineering[J].Neural Computing and Applications,2019,31(12):8195-8203. [13] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10. [14] 黄梦婧,杨海浪.基于PSO的SVM-ARIMA大坝安全监控模型[J].人民黄河,2018,40(8):149-151,156. [15] OCK J H,PARK H K.A Study on the Algorithm of Cash Flow Forecasting Model in the Planning Stage of a Construction Project[J].KSCE Journal of Civil Engineering,2016,20(6):2170-2176. 【责任编辑 张华岩】
