利用表面波对预应力钢筒混凝土管砂浆保护层开裂监测的数值仿真∗

胡少伟 汪 旭 任姝璇 朱开源

(重庆大学 重庆 400045)

0 引言

预应力钢筒混凝土管(Prestressed concrete cylinder pipe,PCCP)是由混凝土管芯、钢筒、高强预应力钢丝和砂浆保护层4 部分组成的大型复合输水管，是在带钢筒的混凝土管芯上环向缠绕预应力钢丝并在其上辊射砂浆保护层而制成的[1−4]。PCCP在我国已经有30年的使用历程，累计使用里程3 万多千米[5]。PCCP 的应用大多为国家基础建设重大工程，敷设里程巨大，关乎国计民生，其结构安全性和运行的稳定性是值得重点关注的技术问题。

由于PCCP 管道在生产和施工中就会产生一定缺陷，运营过程中还将承受极大的水压，环境复杂，易遭侵蚀，达到一定工作时间后PCCP管道的砂浆保护层会出现开裂和剥落，导致预应力钢丝遭受腐蚀进而断裂，最终出现爆管等严重后果[1−4]。因此，对PCCP 砂浆保护层的裂缝发展进行监测能够有效预测和预防力钢丝的断裂。目前，关于PCCP砂浆保护层开裂监测的研究很少，本文在基于此背景下，利用PZT表面应力波动法对PCCP保护层裂缝发展进行数值仿真研究，结果表明该方法对裂缝发展敏感，有极强的实用价值。

1 模型的建立与优化

1.1 几何尺寸及材料参数

在本文数值仿真研究中，利用ABAQUS 有限元软件模拟了对埋置式PCCP 砂浆保护层的开裂监测，所选用的压电材料为PZT-5A。PCCP从内而外依次为内管芯、钢筒、外管芯、预应力钢丝、砂浆保护层，如图1所示。PCCP实体模型尺寸及其材料参数列于表1～2中。

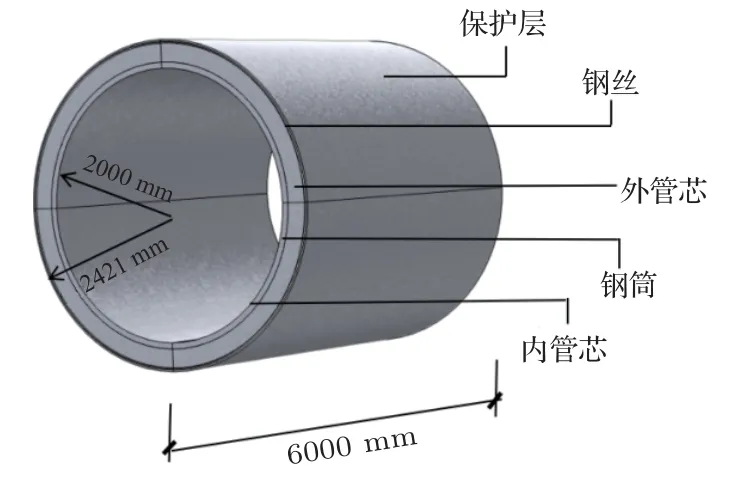
图1 PCCP 模型Fig.1 PCCP model

表1 PCCP 模型各组分尺寸Table 1 Sizes of PCCP Components(单位：mm)

表2 材料参数Table 2 Materials parameters

PCCP 在实际生产、施工、运营过程中可能出现的裂缝形式有环向裂缝和纵向裂缝。由于两种裂缝形式的监测原理和效果理论上是一致的，所以本文选择环向裂缝做重点研究。环向裂缝布置于一半管长处，激励端PZT 与接收端PZT 关于裂缝对称布置，布置方式如图2所示。

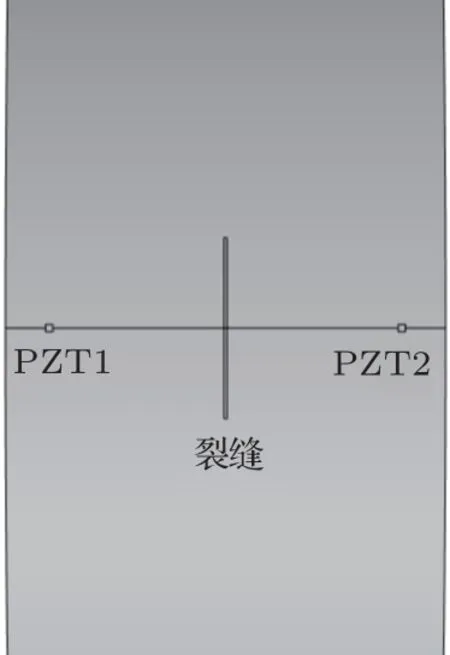
图2 PZT 布置图(俯视)Fig.2 Layout of PZTs(Top view)

1.2 模型的简化

由于模型过大，网格划分单元数量繁多，运算时间过长，因此，在模型计算前进行几方面的合理简化。首先将单节6000 mm 的管道长度缩短至1500 mm，如图3所示。其次考虑到文献[6–11]提出的应力波随传播路径快速衰减特点以及本文中所模拟的内径4000 mm 管道环向周长之大，可以将PCCP 模型只保留上半部分，即忽略表面应力波由裂缝一侧PZT 片绕过管道圆周到达另一个PZT 片的可能性，计算模型如图4所示。另外，由于本文主要采用表面应力波来监测砂浆保护层开裂，表面波沿壁厚方向衰减迅速，因此将PCCP 管壁内的预应力钢丝、内管芯混凝土、钢筒去除，仅保留砂浆保护层和与之相邻较厚的外管芯混凝土。最后，在对比了同一个工况下10T和15T的计算结果(T为频率为表面应力波的周期)后发现，二者在共有的时间段内即10T内结果一致，且后期波形幅值稳定，如图5所示。因此，计算时长均采用10T来计算。

图3 1.5 m PCCP 管Fig.3 1.5 m PCCP

图4 一半PCCP 管模型示意图Fig.4 Schematic of half the PCCP model

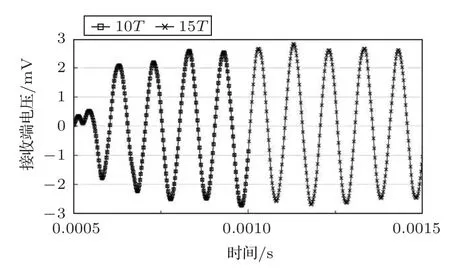
图5 10T 与15T 接收端电压对比图Fig.5 Receiving terminal voltage comparison between 10T and 15T

1.3 输出信号的稳定性优化

由于PZT 接收端信号的稳定性会影响监测效果的判断，所以本小节探究了导致PCCP 砂浆保护层开裂监测模型的输出信号产生不稳定现象的主要原因：模型结果输出步长、网格精细程度、电压源频率及压电片间距。

为保证数据输出时所绘制的电压曲线圆顺，因此在对比了0.1T、0.05T、0.02T(T=0.0001 s，对应本文研究中频率最低的10 kHz 的表面应力波)的结果输出后，发现0.02T已经满足精度要求，因此将输出时间步长设定为0.02T。

网格的划分会直接影响仿真软件计算结果的精度，过于精细会导致计算时间成本的增加，而网格过于粗糙则会直接导致计算结果误差过大。为保证结果的有效性，对于砂浆保护层要求单个波长包含的单元个数在15 以上[12](极细化)，而对于内管芯混凝土则要求6 个以上即可(常规)。

一般情况而言，监测频率越高对损伤的识别更加精确，但从文献[6–7]中不难发现，频率越高会导致应力波衰减越快。因此，需要确定较为合适的频率才利于判断裂缝的发展。为了探究频率对接收信号稳定性的影响，在同一种工况下，以同一种网格划分方式下，且压电片间距都为0.6 m 时，用10 kHz、20 kHz、30 kHz、40 kHz 分别计算，导出接收端电压信号，进行比较。如图6～9 所示，10 kHz 时，波形最为稳定，幅值波动不大，且无畸变现象；20 kHz时，波形的幅值已经产生了一定的波动，但波形完整，无畸变现象；但当频率增加到30 kHz 和40 kHz时，波形已经非常不稳定，且幅值非常低。由此可见，频率过高时波能耗散迅速，导致接收端接收信号微弱，且电压曲线畸变严重。综合以上数值仿真结果，后续计算将会选用20 kHz 以下频率作为激励源频率。

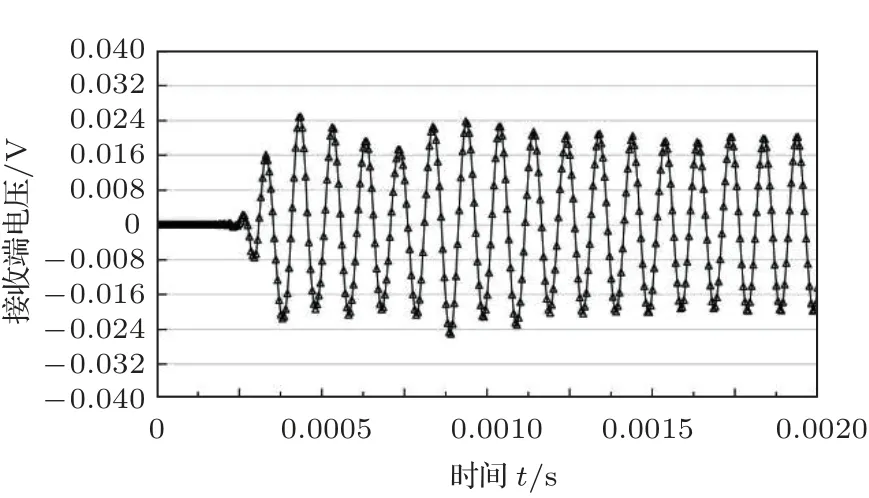
图6 电压源频率为10 kHz 时的接收端电压信号Fig.6 Receiving voltage under 10 kHz source frequency

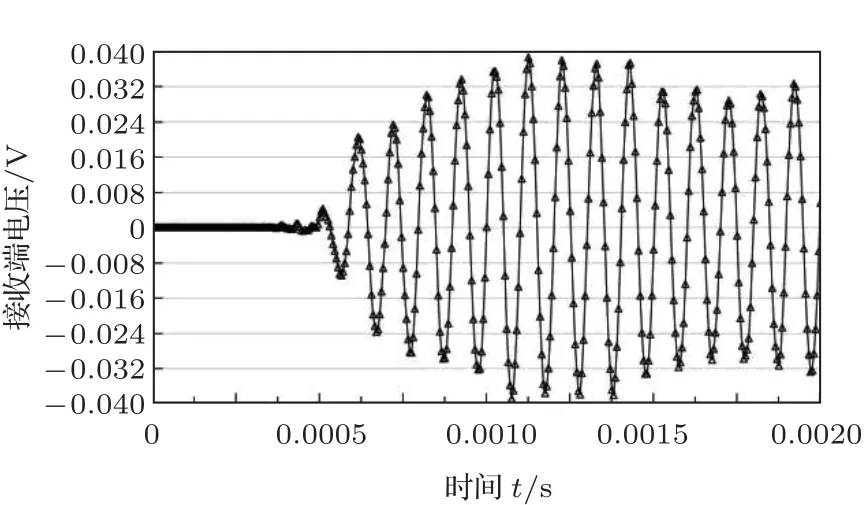
图7 电压源频率为20 kHz 时的接收端电压信号Fig.7 Receiving voltage under 20 kHz source frequency

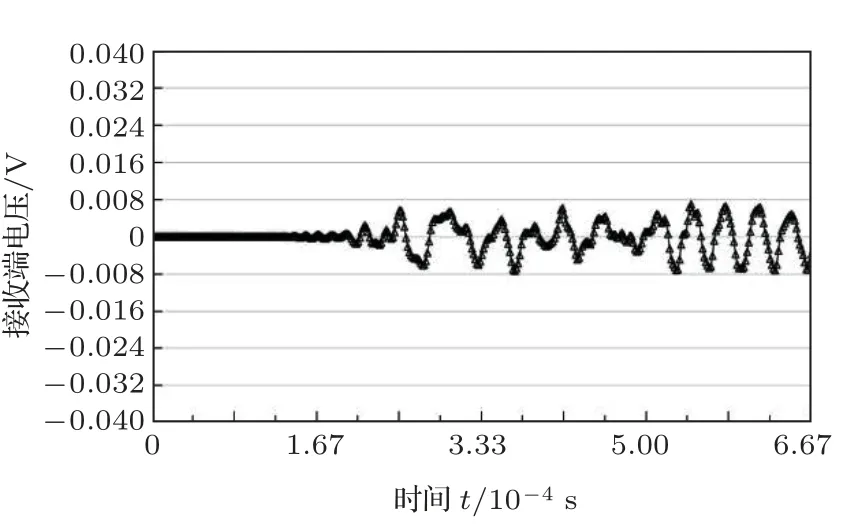
图8 电压源频率为30 kHz 时的接收端电压信号Fig.8 Receiving voltage under 30 kHz source frequency

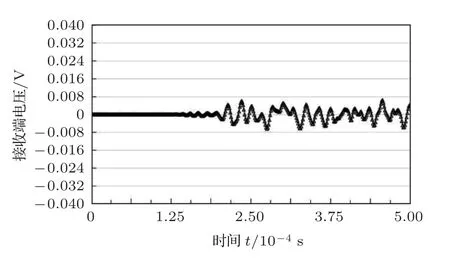
图9 电压源频率为40 kHz 时的接收端电压信号Fig.9 Receiving voltage under 40 kHz source frequency

考虑到表面应力波的形成需要一定的源偏移距(即表面波的形成需要一定的距离，此后才能形成稳定)，而源偏移距又与激励频率直接关联，因此，在综合频率对接收端电压信号的影响后，本文选择10 kHz 作为研究的主要电压源频率，并将压电片之间的距离按0.4 m、0.6 m、0.9 m、1.1 m、1.2 m 进行变化和计算。结果表明，当间距为1.2 m 时，信号幅值较为稳定，且幅值相对1.1 m 时不降反增，因此确定1.2 m 作为频率10 kHz 情况下的最优压电片间距。

2 基于表面应力波的PCCP裂缝发展监测模拟

本节分别改变裂缝的长度、深度、宽度、电压源频率，比较不同工况下接收端电压信号之间的相对幅值差及波形变化，采用的压电片布置方式均为表面粘贴式，即利用表面应力波进行监测。

2.1 裂缝长度影响分析

在小本节中有两个对照组。第一组将宽度固定为15 mm，深度固定为25 mm(截面尺寸较小)，长度分别设置为400 mm、800 mm、1200 mm，电压频率选定为10 kHz。电压时程曲线及其对应幅值如图10～11 所示。可见接收端信号随长度增加无显著变化。

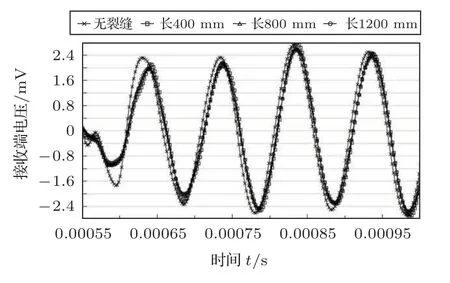
图10 裂缝宽10 mm、深25 mm 工况下长度的影响Fig.10 Influence by the crack length(10 mm width,25 mm depth)

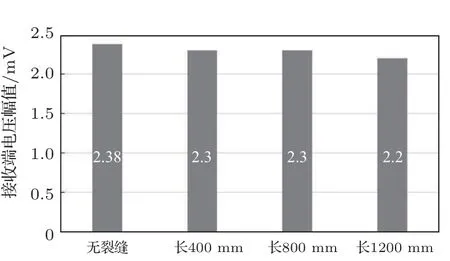
图11 裂缝宽10 mm、深25 mm 工况下幅值随长度的变化Fig.11 Amplitude change with the crack length(10 mm width,25 mm depth)

考虑到当裂缝宽度较窄、深度较浅时，面波可以顺沿裂缝底部传播，而传播途径增加不多不会造成过多能量耗散且裂缝断面反射波能量占比较少，所以在第二组对照组中将裂缝的宽度增加到30 mm，深度增加到34 mm(即预应力钢丝顶部)，长度分别设置为600 mm 和1200 mm，其电压时程曲线及对应幅值如图12～13 所示。此时有裂缝情况较于无裂缝情况幅值有明显的降低。这是因为当裂缝产生后，裂缝对应力波造成的反射及传播路径的增加致使能量的衰减。但随着裂缝长度的增加幅值仍然没有明显变化，所以接收端电压信号对长度变化敏感度较低。

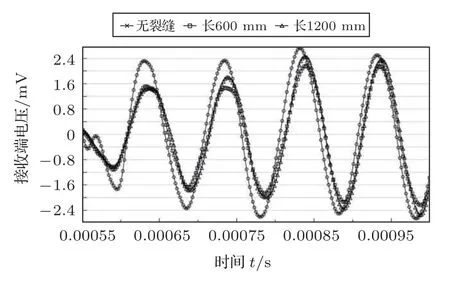
图12 裂缝宽30 mm、深34 mm 工况下长度的影响Fig.12 Influence by the crack length(30 mm width,34 mm depth)

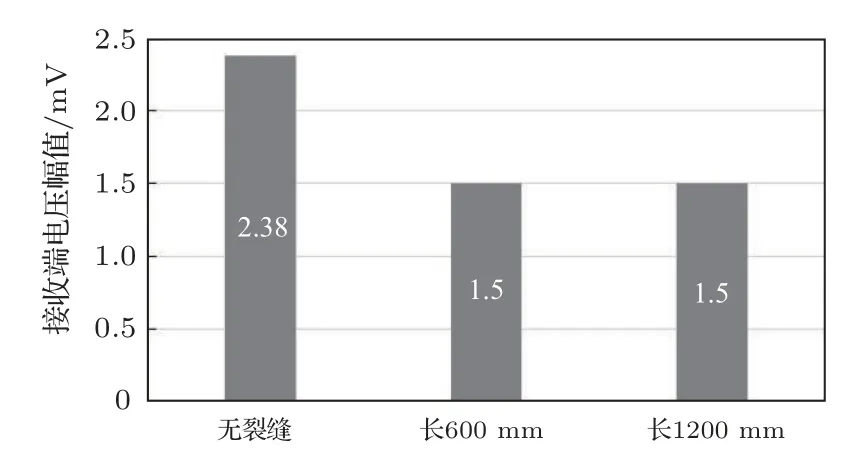
图13 裂缝宽30 mm、深34 mm 工况下幅值随长度的变化Fig.13 Amplitude change with the crack length(30 mm width,34 mm depth)

2.2 裂缝深度影响分析

由2.1 小节的两个对照组可以发现，长度的增加对接收端信号的影响较小，无需将裂缝长度设置过大。所以在第一个深度组中，将长度设置为600 mm，将宽度设置为30 mm，激励端电压频率仍然保持10 kHz，深度按10 mm、15 mm、25 mm、34 mm 变化，分别计算得出电压时程曲线及其对应幅值如图14～15所示。

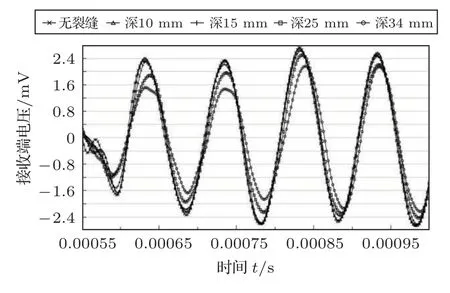
图14 裂缝长600 mm、宽30 mm 工况下深度的影响Fig.14 Influence by the crack depth(600 mm length,30 mm width)

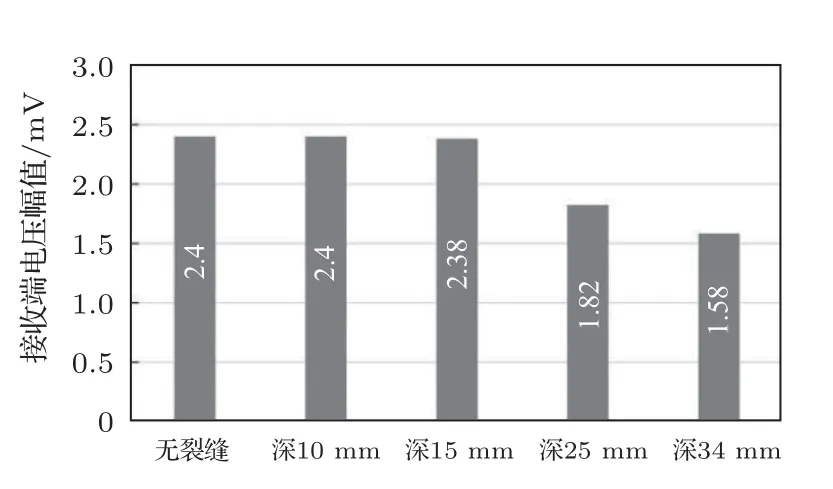
图15 裂缝长600 mm、宽30 mm 工况下幅值随深度的变化Fig.15 Amplitude change with the crack depth(600 mm length,30 mm width)

可以看出，裂缝深度发展到10 mm 及15 mm时，幅值变化相较于无损情况变化并不大的。但是当裂缝深度发展到25 mm 甚至34 mm 时(即15 mm之后)，电压幅值出现大幅下降。无裂缝与深度为34 mm之间的电压幅值相差了0.8 mV，占无裂缝情况下幅值的33.3%，这个数值非常可观。这里需要强调的是砂浆保护层属于后喷部分，对于整个PCCP管道刚度和承载力贡献不大，砂浆保护层裂缝在初步发展阶段中并不影响其正常工作，但当裂缝开展到预应力钢丝的表面(深度为34 mm)时，外界腐蚀介质的进入极易造成预应力钢丝锈蚀，日积月累，一定数量的预应力钢丝因锈蚀程度的加深在内外压作用下就会断裂，从而造成管道承载力不足而爆管。本小节所模拟的监测方法对裂缝深度的发展灵敏度高，这对于PCCP 砂浆层的裂缝监测是非常有价值的。

为了避免结果的偶然性，在第二个对照组中将宽度减小至10 mm，长度为600 mm，深度仍按10 mm、15 mm、25 mm、34 mm 变化，电压时程曲线及其对应幅值如图16～17所示。

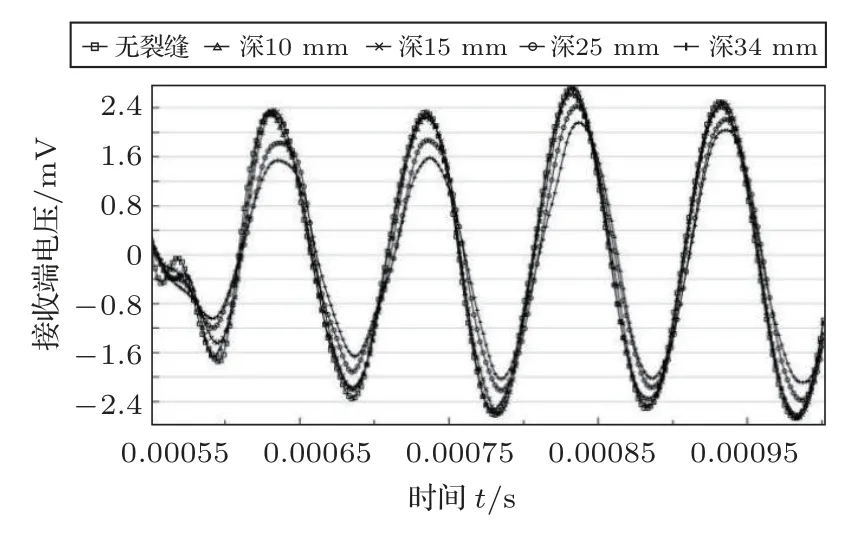
图16 裂缝长600 mm、宽10 mm 工况下深度的影响Fig.16 Influence by the crack depth(600 mm length,10 mm width)

由图16和图17可以发现，减小宽度尺寸后，电压的变化规律依然是相同的——随着裂缝深度的增加，电压幅值减小，且深度发展到15 mm 之后，电压幅值发生大幅的下降，且裂缝深度发展到34 mm时，电压幅值也下降了0.8 mV，同样占无裂缝情况下幅值的33.3%。

2.3 裂缝宽度影响分析

在本小节也设有两个对照组。第一组将长度设置为600 mm，深度设置为34 mm，而宽度按照10 mm、30 mm、50 mm、100 mm、150 mm 变化，激励电压频率为10 kHz。电压时程曲线及其对应幅值如图18～19所示，有裂缝状况时的幅值整体都小于无裂缝状况，当裂缝宽度大于50 mm 之后，接收端电压信号的幅值开始发生明显的上升，由70 mm 发展到150 mm，幅值增加0.4 mV。

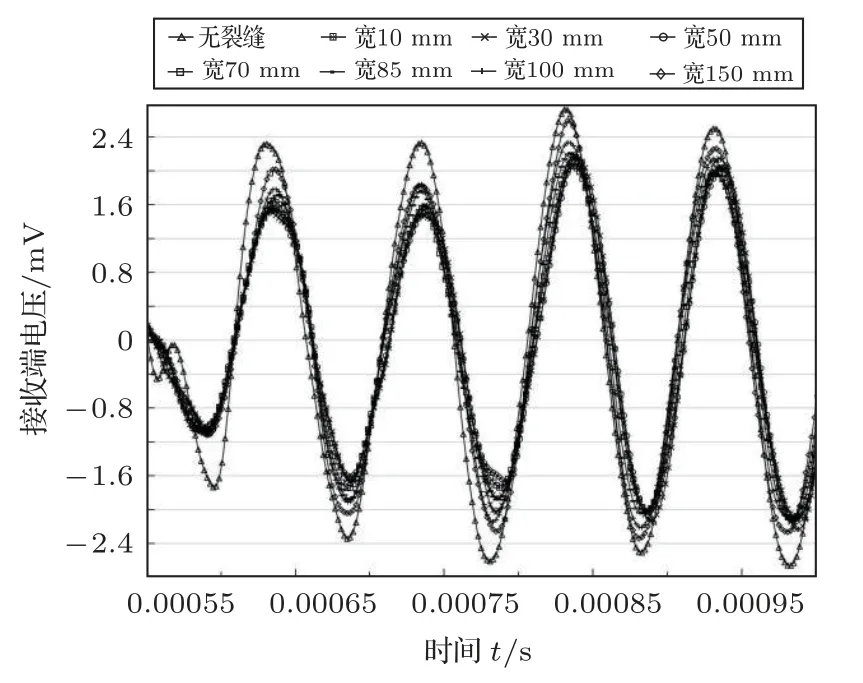
图18 裂缝长600 mm、深34 mm 工况下宽度的影响Fig.18 Influence by the crack width(600 mm length,34 mm depth)

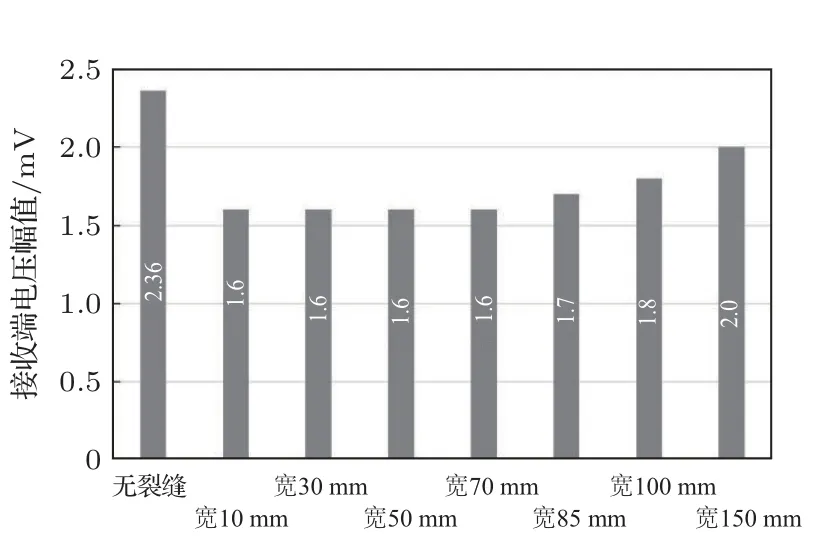
图19 裂缝长600 mm、深34 mm 工况下幅值随宽度的变化Fig.19 Amplitude change with the crack depth(600 mm length,34 mm depth)

考虑到第一组裂缝深度较深，可能对接收端的电压幅值有一定影响，第二个对照组将长度固定为600 mm，深度减小为20 mm，裂缝的宽度依次设为10 mm、30 mm、50 mm、100 mm、150 mm。电压时程曲线及其对应幅值如图20～21 所示。在本组对照组中，也可以清晰地看到随着宽度的增加，接收端的电压信号幅值也在缓慢增大。但这组的突增区间是处于100～150 mm，较前组大。

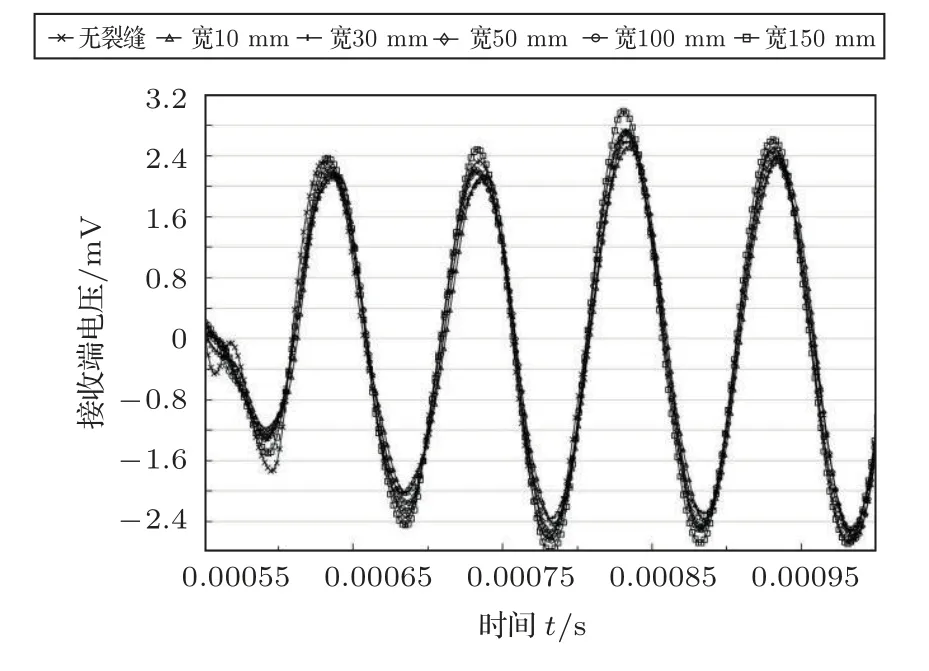
图20 裂缝长600 mm、深20 mm 工况下宽度的影响Fig.20 Influence by the crack width(600 mm length,20 mm depth)

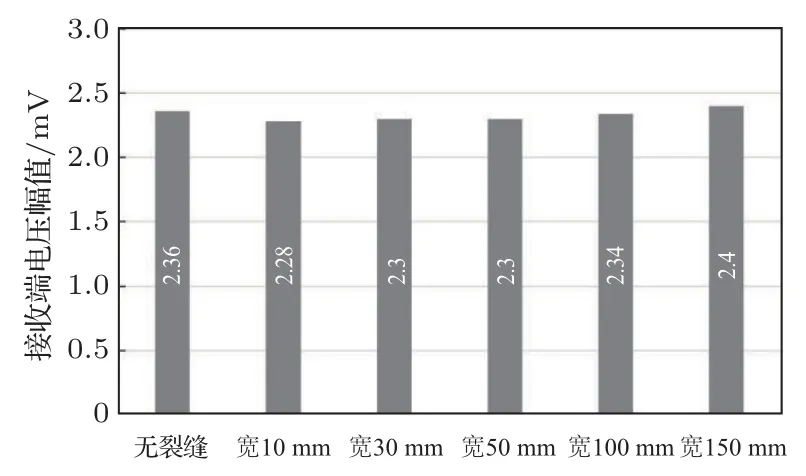
图21 裂缝长600 mm、深20 mm 工况下幅值随宽度的变化Fig.21 Amplitude change with the crack depth(600 mm length,20 mm depth)

为找出接收端电压幅值随裂缝宽度变化的原因，在第一个对照组中，在靠近接收端PZT 的裂缝断面外侧增设了1 片PZT。结果显示，当裂缝宽度在10～70 mm 范围内时，所增设PZT 片的信号幅值小于裂缝宽度在85～150 mm范围时的信号幅值，即意味着裂缝宽度较小时的反射波能量大于裂缝宽度较大时，这也就解释了裂缝宽度在达到一定值后，接收端电压信号幅值出现了不降反增的原因。

虽然一般研究中所讨论的裂缝宽度是0.5～1.5 mm，而本文中讨论的裂缝宽度较长，在实际工程中对应的是砂浆保护层的块状剥落，涉及遭受锈蚀的预应力钢丝的数量(预应力钢丝是按照固定螺距进行缠绕)，也同样具有研究意义。

2.4 频率影响分析

在2.3 节中，已经讨论过10 kHz、20 kHz、30 kHz、40 kHz 情况下的接收端电压信号，并得出结论：压电片间距0.6 m 时，30 kHz 和40 kHz由于衰减过快，幅值很小且波形存在畸变情况，不适于本次模拟的情况，所以应选取20 kHz 以下的频率。又由2.1～2.3 小节的长度、深度、宽度对照组可以看出，深度对于接收端电压信号的影响最为明显，所以在本节中，将具体讨论频率为5 kHz和15 kHz时的深度对照组情况，并与频率为10 kHz 时的深度对照组进行比较，

首先将频率设置为5 kHz，其他情况与2.2 节中10 kHz 情况下相同：裂缝长度为600 mm，宽度为30 mm，深度由10 mm、15 mm、25 mm、34 mm 变化，电压时程曲线及其对应幅值如图22～23所示。

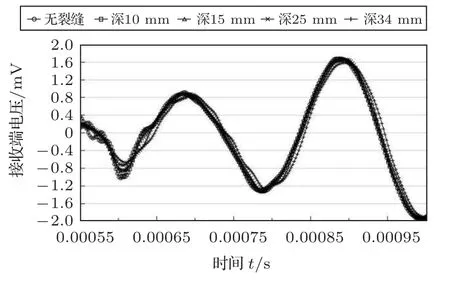
图22 裂缝长600 mm、宽30 mm 工况下深度的影响(5 kHz)Fig.22 Influence by the crack depth(600 mm length,30 mm width,5 kHz)

根据图22～23，采用5 kHz 进行深度组监测效果不佳，不同工况之间的波形图几乎重合，没有明显的变化，并且波形图不稳定存在畸变，说明这种情况下5 kHz 的监测效果不如10 kHz，且此时1.2 m 也并不是5 kHz 对应的最佳距离(波形存在畸变)。分析其原因，由于λ＝u/f，其中λ为波长，u为波速，f为频率。其中波速由介质决定，相同的介质中波速相同。所以在同一介质中，频率越小，波长越长，表面应力波的形成需要更大的源偏移距(这点可以由图23和图25的无裂缝时输出电压幅值论证得到)，在两端压电陶瓷片间距相对较近时无法对裂缝进行有效识别。

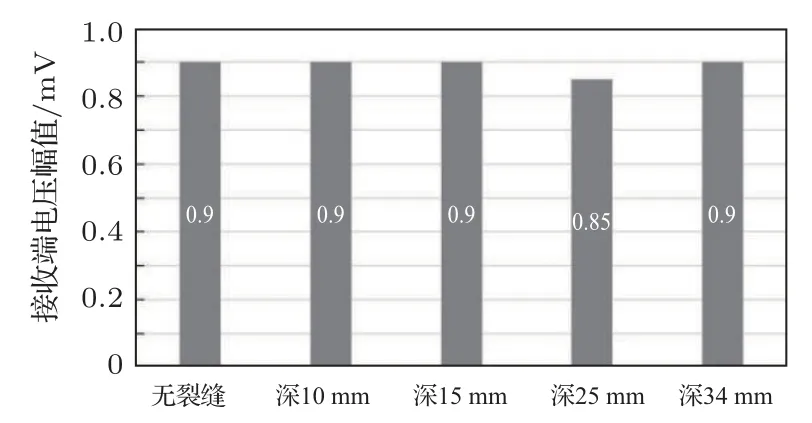
图23 裂缝长600 mm、宽30 mm 工况下幅值随深度的变化(5 kHz)Fig.23 Amplitude change with the crack depth(600 mm length,30 mm width,5 kHz)

将频率设置为15 kHz，其他设置完全相同，电压时程曲线及其对应幅值如图24～25 所示。用频率15 kHz 作为激励端电压时，随着深度增加，接收端电压幅值也有明显的降低。并且和10 kHz 时一样，裂缝深度为10 mm 和15 mm 时，变化不是特别明显，但是当裂缝深度发展到25 mm 和34 mm时，电压幅值大幅下降。无裂缝与深度为34 mm 时电压幅值相差有1.6 mV，占无裂缝情况下幅值的61.5%，是用10 kHz 监测时的1.5 倍。但是裂缝深度为34 mm 时，接收端的电压波形图出现了畸变，说明用15 kHz 监测时，1.2 m 并不是其对应最优接收距离，此处不再探讨15 kHz 的最适接收距离，探究方法与2.3节一致。

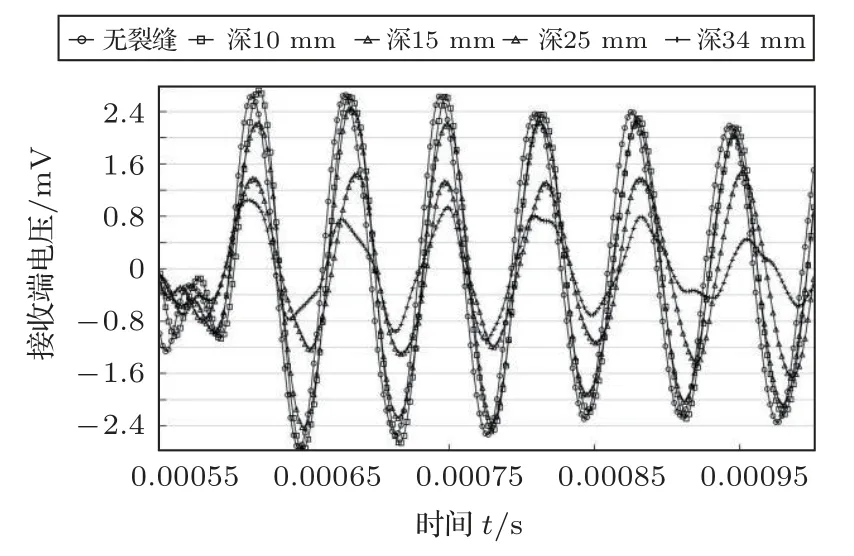
图24 裂缝长600 mm、宽30 mm 工况下深度的影响(15 kHz)Fig.24 Influence by the crack depth(600 mm length,30 mm width,15 kHz)

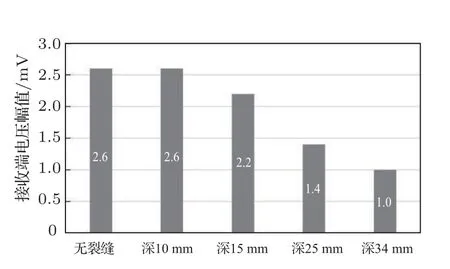
图25 裂缝长60 0mm、宽30 mm 工况下幅值随深度的变化(15 kHz)Fig.25 Amplitude change with the crack depth(600 mm length,30 mm width,15 kHz)

2.5 总结及原因分析

本节设置了长度、深度、宽度、频率4 个对照组，探讨了裂缝发展时接收端电压信号的变化规律。总结得到以下4 点：(1)其他条件相同，随着裂缝长度的增加，接收端电压变化规律不明显。(2)其他条件相同，随裂缝深度的增加，接收端电压幅值减小，且当深度发展到15 mm 以上时，幅值出现大幅下降，相对无损情况最大幅值差为0.8 mV，占无裂缝时电压值的33.3%。(3)其他条件相同，随裂缝宽度的增加，接收端电压幅值起初变化不大，当宽度发展到一定程度时，幅值会发生明显增加。(4)压电片间距为1.2 m 时，5 kHz 监测效果不佳，幅值没有明显变化；15 kHz 监测效果明显，最大幅值差达1.6 mV，为无裂缝时电压值的61.5%，是用10 kHz监测时的1.5 倍，但波形有畸变，1.2 m 不是其最佳接收距离。

根据图26～28，可以对以上的规律做出合理解释。由于应力波是以激振处为圆心向四周传播的，传播越远，半径也就越大。此时裂缝的长度相对于波阵面的弧长而言就比较小，所以裂缝长度对电压信号影响最小，由图26及图27可以清晰地看出这一规律。另外，观察图28可以发现，应力波在深度方向的衰减非常迅速，而当应力波传播至裂缝处时只能沿裂缝的底面传播到另一端，因此裂缝深度的影响最大，宽度次之。

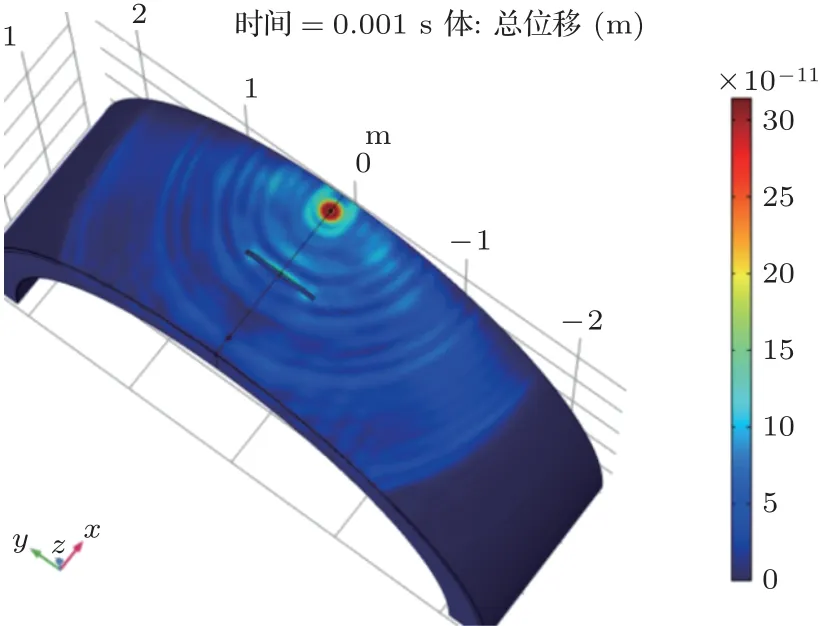
图26 面波监测裂缝长600 mm、宽30 mm、深34 mm 下的位移场(10 kHz)Fig.26 Displacement field under surface wave monitoring(600 mm length,30 mm width,34 mm depth,10 kHz)

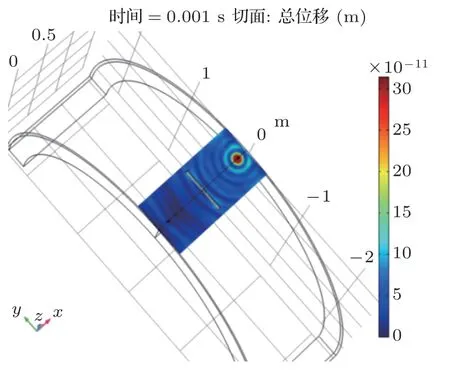
图27 x-y 平面位移场(10 kHz)Fig.27 Displacement field for xy plane(10 kHz)

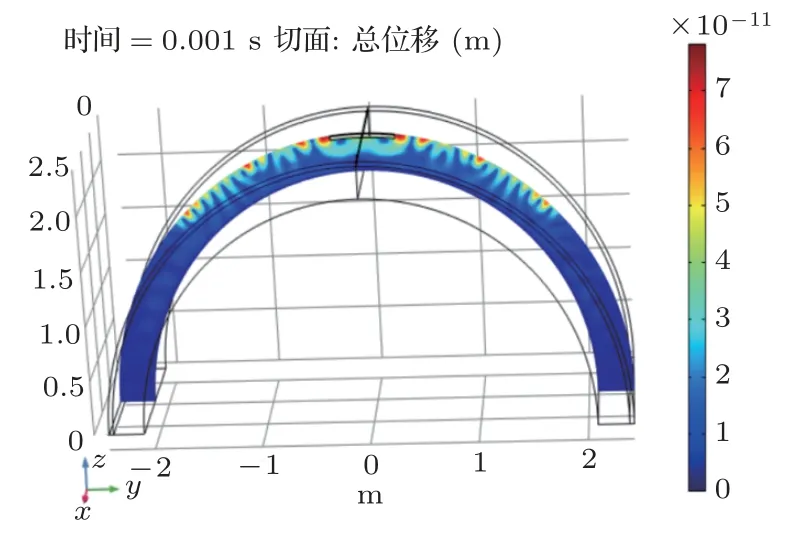
图28 y-z 平面位移场(10 kHz)Fig.28 Displacement field for yz plane(10 kHz)

3 不同应力波型对PCCP砂浆保护层裂缝深度发展监测效果对比

考虑到裂缝深度发展对PCCP 内预应力钢丝的危害性，在本节中对比了表面应力波与体应力波这两种不同应力波型对裂缝深度发展的监测效果。

体波监测模型中，保持压电片尺寸不变，将两片PZT 间距保持1.2 m 距离且竖直放入砂浆层内，压电片的极化方向与管长方向一致，压电片中心相距砂浆层表面17 mm。裂缝形式和前述模拟相同，仍为环向裂缝。将裂缝长度设置为600 mm，宽度设置为30 mm，深度分别设置为10 mm、15 mm、25 mm、34 mm 展开深度对照组。网格划分与2.3 节划分保持一致，模型如图29所示，电压时程曲线及其对应幅值如图30～31 所示，体波监测时的体位移图如图32所示。

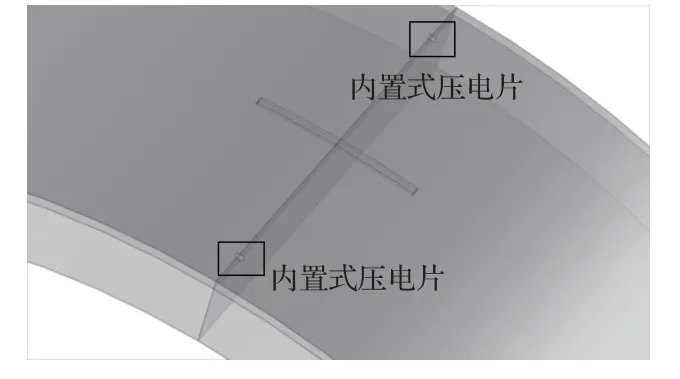
图29 基于体波的监测模型(内置式)Fig.29 Monitoring model based on body wave(embedded)

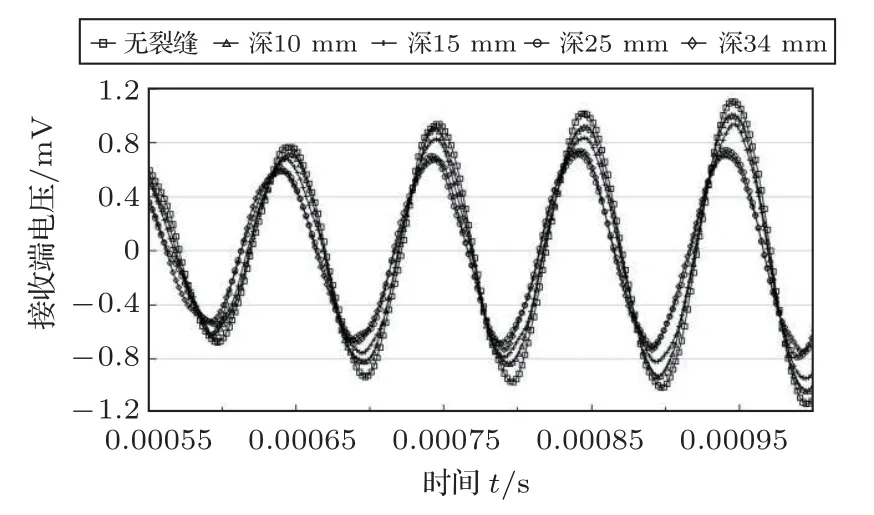
图30 裂缝长600 mm、宽30 mm 工况下深度的影响(体波10 kHz)Fig.30 Influence by the crack depth(600 mm length,30 mm width,10 kHz)

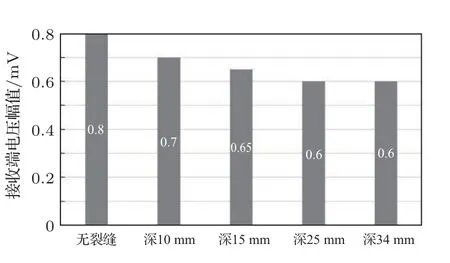
图31 裂缝长600 mm、宽30 mm 工况下幅值随深度的变化(体波10 kHz)Fig.31 Amplitude change with the crack depth(600 mm length,30 mm width,10 kHz)

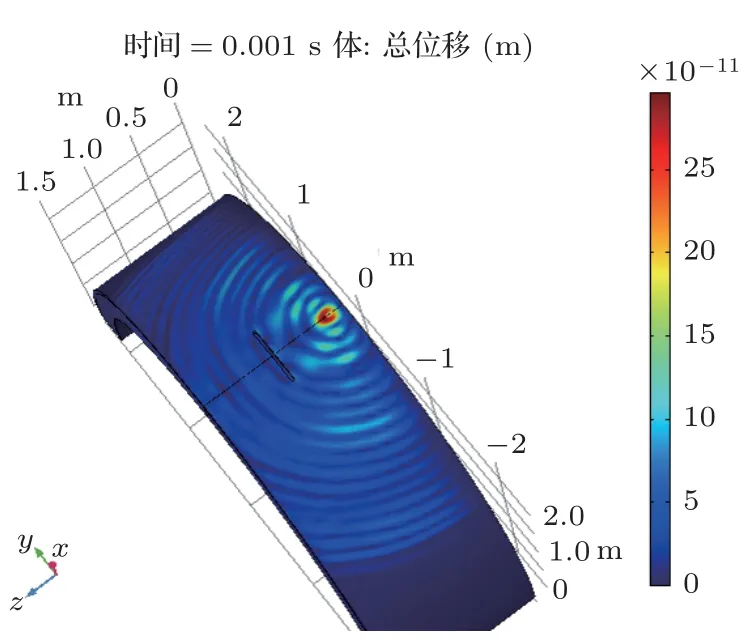
图32 体波监测裂缝长600 mm、宽30 mm、深34 mm 情况下的位移场(10 kHz)Fig.32 Displacement field under body wave monitoring(600 mm length,30 mm width,34 mm depth,10 kHz)

由图31可以看出，在其他条件完全相同的情况下，当没有裂缝产生时，用体波测量时的幅值为0.8 mV，而用面波测量时幅值为2.4 mV(如图17所示)。从图30和图31还可以看出，用体波进行深度组模拟有着同样的规律——随着裂缝深度的增大，电压幅值呈下降趋势。但是从无裂缝发展到裂缝深度为34 mm，幅值只下降了0.2 mV，只有面波测量时的1/4。所以在压电片间距1.2 m、激励端频率为10 kHz情况下，面波的监测效果相对较好。

另外，将图32与图26进行对比可以发现，采用面波监测时的总位移最大值(32×10−11m)大于采用体波监测时的总位移最大值(29×10−11m)，这也符合面波蕴含能量大于体波能量的客观规律[13]。

4 结论

(1)模型结果的输出步长、网格划分精细度、频率以及压电片间距是影响稳定性的主要因素。可以通过缩短模型结果输出步长、细化网格、选择合适的频率及压电片间距，消除以上不稳定因素的影响。

(2)接收端信号随裂缝深度增加时变化最为明显，接收端电压随裂缝深度增加时的最大下降幅值可达0.8 mV，占无裂缝时电压值的33.3%，对预应力钢丝是否即将遭受腐蚀具有预警作用；而接收端信号幅值在裂缝宽度达到一定值后会缓慢增加，随裂缝长度的增加变化不明显。

(3)对于管线而言，PZT 片之间的间距越大所需PZT 片个数越少，监测总成本越低，这也就要求尽量地使用较低频率(所需源偏移距大)进行监测，然而频率过低对PCCP 砂浆保护层裂缝的开裂监测敏感度也会下降。若依然采用较低监测频率时的PZT 间距使用高频去进行监测(表面波早已稳定形成)，对前期裂缝发展更为敏感，但由于高频应力波衰减过快，会导致对后期裂缝的发展过程无法准确识别，因此需要找到一种折衷的信号频率值及相对应的压电片间距。本研究中，在保持压电片间距相同(1.2 m)的情况下，5 kHz 的监测效果不佳，15 kHz 的前期监测效果较好，其接收端电压随裂缝深度增加时的最大下降幅值是用10 kHz 监测时的2 倍，但由于其波形后期出现畸变(电压值小)，综合考虑10 kHz为监测的最优频率。

(4)体波与面波包含的能量相差悬殊，符合客观规律，且用面波监测时的最大下降幅值为体波时的4 倍，所以在1.2 m 间距及10 kHz 电压源频率条件下，面波监测的效果较好。